新型全液压重载锻造机器人机构设计及分析

李阁强　王　帅　邓效忠　周　斌

1.河南科技大学，洛阳，471003　　2.安阳锻压机械工业有限公司，安阳，455000



新型全液压重载锻造机器人机构设计及分析

李阁强1王帅1邓效忠1周斌2

1.河南科技大学，洛阳，4710032.安阳锻压机械工业有限公司，安阳，455000

针对全液压重载锻造机器人载荷大、搬运速度快和定位精度高的特点提出了一种新型机构方案，该方案能够实现车身回转、夹钳伸缩、夹钳升降、夹钳回转和钳头夹紧五个自由度的运动，其运动主体为一种混联机构，由三组平行四边形连杆机构构成，采用三组液压缸并联驱动，可有效增大机器人工作空间，使负载分配合理，易于控制。建立了运动学和动力学模型，采用正弦曲线将机器人夹钳末端的位移规划为直线运动，在MATLAB中求解出机器人的工作空间，得到了直线运动下各组液压缸的位移和驱动力变化曲线，验证了该模型的正确性和机构的合理性，为重载锻造机器人机构设计提供了一种解决方案。

新型重载锻造机器人；运动学分析；工作空间；动力学分析

0　引言

全液压重载锻造机器人是实现模锻自动化的重要设备之一，它的主要任务是在锻造过程中对锻件进行工序转移，配合模锻液压机进行锻造工作，对于提高锻造精度和效率、降低能耗具有重要的作用[1]。工件转移时对时间和精度要求高，若转移时间过长或者定位精度不准，锻件的温度和性能就可能达不到要求，进而导致工件需要重新回炉，甚至报废。与普通上下料机器人相比，全液压重载锻造机器人的突出特点是大载荷(已见的国外模锻搬运机器人载荷能力达到5 t)，以及大载荷下的操作灵巧性、快速性、高定位精度、恶劣工况下长期服役的高可靠性[2-4]。目前世界上只有德国的DDS公司和GLAMA公司具有生产该类成熟产品的能力，产品主要特点是全液压驱动设计，采用机械耦合铰接臂连接，机身尺寸小，工作空间大。关于液压重载锻造机器人的研究未见报道，相关研究主要是针对锻造操作机机构的运动学、动力学以及液压控制系统的[5-8]。但锻造操作机不同于锻造机器人，它在锻造加工中直接参与锻造，和压机配合实现锻造一体化加工，其运动速度慢，快速响应能力要求不高，工作空间小。

近年来，我国在大飞机、轨道交通、大型海洋钻井设备、核电和火电等重大装备领域发展迅猛，对大吨位大尺寸模锻件有较大需求。而我国的大型重载锻造机器人主要依赖进口，不仅价格昂贵、供货周期长，而且我国大型锻件的制造加工技术受制于人。因此，自主研发重载锻造机器人对我国重大装备制造业的发展有重要意义。

大载荷下的运动速度和定位精度是锻造机器人的重要性能指标，为达到该性能指标，机构设计是关键。为此，本文对重载锻造机器人机构进行研究，提出了一种新型混联机构方案，建立了运动学和动力学方程，设计了机构参数，求解了机器人的运动空间，进行了运动学和动力学仿真验证，为全液压重载锻造机器人的研制提供了一种解决方案。

1　全液压重载锻造机器人新型混联机构设计

1.1设计参数要求

与该重载机器人配合的是四立柱12 500 t模锻液压机，根据其在锻造过程中的功用及要求，规划出机器人的主要动作，包括车身行走、车身回转、夹钳伸缩、夹钳升降、夹钳回转和钳头夹紧等要求，提出的技术参数要求见表1。

表1　新型锻造液压重载机器人技术参数

1.2机构方案

根据技术参数要求，提出全液压重载锻造机器人机构方案，如图1所示。重载机器人机构主要包括机架、行走装置、连杆机构和驱动单元等，其中，机架通过铰接点和大臂以及各组液压驱动单元相连接；行走装置主要通过底座中的液压马达驱动车身在导轨上行走的动作；连杆机构由大臂、小臂、连杆和连接板组成，它与驱动单元中的液压缸直接相连，在驱动单元的作用下，使夹钳末端按照规划轨迹运动；驱动单元包括提升液压缸、提升辅助液压缸、水平驱动液压缸、泵站以及夹钳回转马达和车身回转马达，通过控制电液比例阀使其为机器人的各个动作提供驱动力。机器人整体质量约40 t，在最大伸展状态下的外形尺寸长约10 m，宽约4 m，高约8 m，整机装机功率约150 kW。

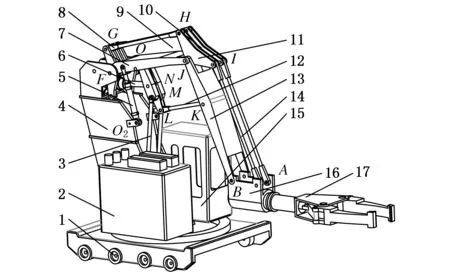
1.底座　2.液压泵站　3.提升缸　4.机架　5.提升辅助缸　6.水平驱动缸　7.大臂　8，9，10，12，14.连杆　11.连接板　13.小臂　15.驾驶室　16.夹钳驱动机构　17.夹钳图1　新型液压重载机器人结构图

如图2所示，新型全液压重载锻造机器人使用了一种由3组平行四边形连杆机构和驱动液压缸组成的串并联混联机构，该机构是机器人的运动装置主体，其中的3组平行四边形分别为GFJH、IJBA和LKJO。平行四边形GFJH中，GF直接焊接在机架上，即GF与水平方向的夹角固定，由平行四边形的特性可知，HJ与水平方向的夹角不变；IJBA通过连接板HJI和J点铰接，由于JH和JI的夹角恒定，令JI与水平面平行，则钳头的2个铰接点A、B所在边也与地面平行，通过平行四边形GFJH和IJAB的作用，保证了钳头与水平面始终平行；平行四边形LKJO主要起到放大驱动单元行程的作用，其中OJ和JK分别与FJ和JB重合，且OJ的长度小于FJ的长度，JK的长度小于JB的长度，当液压缸驱动LKJO产生运动时，由于机构的相似性，驱动单元的位移被放大。

图2　连杆机构简图

图2所示的机构中包含3组驱动单元，每组含有2个液压缸，分析时将每组中的2个液压缸简化为一个进行分析。举升缸的缸筒通过铰链O1铰接在机架4的耳座上，上端通过M点铰接在连杆OL上；提升辅助缸的缸筒通过O2铰接在机架的耳座上，缸杆端通过F点铰接在大臂FJ上；水平驱动缸缸筒通过铰链O3铰接在机架的耳座上，杆端通过N点铰接在连杆OL上。采用双缸驱动方案，使得机构承受负载的能力大大提高，分配到单个液压缸的作用力减小，控制特性好。

该机器人的机构采用3组平行四边形结构互相组合，能够保持机器人驱动末端夹钳始终与水平面平行，在快速搬运过程中保证了工件的姿态稳定，提高了在工件放置时的安全性和定位精度，同时平行四边形机构对驱动单元的行程起着放大的作用，增大了工作空间，减小了缸的控制行程，进而减小了机构控制难度，提高了搬运速度，增强了控制特性。更进一步，机器人快速接近目标、减速微调控制时，易于实现精准的定位控制。

1.3机构自由度计算

该机构如图3所示，图中建立了全液压重载机器人底座上的坐标系O4xy，根据修正的Grübler-Kutzbach公式对该机器人的机构进行自由度M的计算：

(1)

式中，d为机构的阶数；n为包括机架在内的构件数目；g为运动副的数目；fi为第i个运动副的自由度。

图3　新型液压重载机器人结构简图

考虑到机身的回转和夹钳的旋转，计算得出该新型机构的自由度为5，满足机器人的动作要求。

2　机构运动学分析

图3所示的机构是一种复杂的耦合机构，使用复数向量法将该机构分解为多个闭合的环状结构，建立机构的向量方程组，每个方程组内至少包含一个长度和角度变化的杆件，以前一个闭合环路的输出解作为后一个方程的输入，最终将机构的向量方程组解出，获得机构运动学的正解和反解。根据闭合矢量法得到闭合矢量方程组：

(2)

式中，LO2F为以O2为起点、F为终点的矢量，其余类推。

根据复数向量法可得系统运动学方程组的复数方程：

(3)

式中，lO2F为线段O2F的长度，其余类推；θ1为提升缸与x轴方向的夹角；θ2为提升辅助缸与x轴方向的夹角；θ3为水平驱动缸与x轴方向的夹角；θ4为FJ与x轴方向的夹角；θ5为AI与x轴方向的夹角；φ1为O2F与x轴方向的夹角；φ2为O1F与x轴方向的夹角；φ3为O3F与x轴方向的夹角；φ4为O3G与x轴方向的夹角；φ5为IH与JH的夹角。

2.1运动学正解

在式(3)中将各个液压缸的长度视为已知量，将夹钳末端位置坐标x、y视为未知量。在第一个闭环矢量方程中，给定驱动液压缸O2F的长度，FP、O2P、θ4的大小均已知，将矢量方程按复数向量法展开，可推导出θ4和θ2的值，在第二个闭环矢量方程中，驱动缸O1M的长度给定，OM、O1F、OF、θ4、φ2已知，同理可推导出θ5和θ1的大小；同理，由第三个闭环矢量方程可得到θ3，由第四个闭环矢量方程可得到x、y的值，由于夹钳始终与地面平行，故夹钳的姿态角为0，由以上方法可以得出夹钳的位置：

(4)

2.2逆运动学反解

运动学反解是对该新型重载机器人机构的夹钳末端给定空间中某点的位置和姿态，然后对各组驱动液压缸的长度变化进行求解。首先对矢量闭合环路1进行求解，由于已知夹钳末端的x、y坐标值，可以得到θ5和θ4的大小；将θ5和θ4作为环路2的输入进行求解，可以得到液压缸2的长度D2和θ2；同理对环路3进行求解可得出液压缸1的长度D1和θ1，对环路4进行求解可以得到液压缸3的长度D3和θ3，由上述过程可得到机构的运动学反解：

(5)

式中，xA、yA为夹钳末端A点的坐标；φ6为O4F与x轴方向的夹角。

以上针对新型全液压重载锻造机械手进行的运动学分析为下一步的机构运动空间和动力学的仿真打下了基础。

3　动力学模型的建立

基于牛顿-欧拉法、虚功原理法和拉格朗日法，建立机构的动力学模型[9]，其中牛顿-欧拉法主要对机构的各个铰接点的受力情况进行分析，计算效率较高，然而当机构比较复杂时，该方法需要建立的方程过多，推导比较繁琐。使用拉格朗日法针对结构较为简单的机构进行分析时，可以较为容易地得出各个关节力的解析式，该方法得出的解析式计算效率高且有利于机构的实时控制，然而对于复杂的机构，解析式不易获得。虚功原理法是一种目前被认为计算效率很高的动力学求解方法[10-12]，由于新型重载机器人机构属于复杂耦合结构，且结构中有复合铰链的存在，故使用虚功原理对机器人机构进行动力学建模，获得夹钳末端在期望位移下的各缸的驱动力变化值。

根据平面机构简图(图2)，将机构中所有的杆件和钳杆视作刚体，同步驱动的双液压缸执行单元简化为一个液压缸执行单元，假设机座不转动，对机构的平面进行分析。图2中，O1、O4、O3、P、F为机构的固定铰链点，坐标系为O4xy，其坐标轴x、y对应的单位矢量分别为i、j。令ui为第i个杆件质心，mi为第i个杆件的质量，Ji为第i个杆件相对质心的转动惯量，θi为第i个杆件的姿态角，设定逆时针为正。vi为第i个杆件在坐标系中运动的绝对速率，Di为液压缸缸杆铰接点到缸筒末端间的距离，则

ui=uxii+uyij

(6)

(7)

其中，ui、vi分别为连杆第i个连杆的质心在绝对坐标系下的位置矢量和速度矢量，令重力加速度矢量g=gj ，则惯性力Fi的表达式为

(8)

对于连杆i(i=1,2,…,11)，由于惯性力Fi和重力Gi在虚位移上做的元功为

δWPi=-Fiδui-Giδui

(9)

将式(8)代入式(9)可得

(10)

驱动力Ni在虚位移上做的功为

δWNi=NjδDj

(11)

除重力和驱动力之外，作用在连杆i质心上的等效外力和外力矩分别为Pxi、Pyi和Ti，其在虚位移上所做的功为

δWPi=Pxiδxi+Pyiδyi+migδyi+Tiδqi

(12)

根据虚功原理可得

(13)

将式(6)～式(12)代入式(13)可得各个驱动液压缸单元的受力Ni的表达式：

(14)

4　夹钳末端位移规划

实际生产中对速度和精度的要求很高，为便于控制，在机器人夹持工件运动时，如图4所示，夹钳末端的运动轨迹规划为垂直方向和水平方向的直线运动是最为合适的。由于负载较大，且机构的运动速度较快，为尽量减少机构在加速和减速过程中产生的冲击和振动，采用正弦曲线进行位移规划，其主要特点是加速度曲线为正弦曲线形式。

图4　新型重载机器人机构运动简图

机构加速度为

a=amaxsin(πt/Tm)

(15)

根据正弦规划的速度方程：

(16)

对以上速度方程积分可得位移方程：

(17)

式中，s1为t1时刻的位移。

结合机器人的工作要求，规划夹钳末端的最大运动速度分别为0.3m/s、0.5m/s、0.7m/s，设夹钳末端开始运动的初始位置坐标为(2500，500)mm，运动时间为6s。其中，0～3s内夹钳末端夹持工件后在水平方向直线运动，0～1s为加速阶段，1～2s为匀速阶段，此时运动速度达到最大，2～3s为减速阶段；在3～6s内末端沿垂直方向直线运动，3～4s为加速阶段，4～5s为匀速阶段，此时运动速度达到最大，5～6s为减速阶段。在MATLAB软件中获得的夹钳在水平和垂直方向的位移曲线如图5所示，图中S1i(i=1，2，3)为夹钳末端在水平方向上的位移规划曲线，其最大运动速度分别为0.3m/s、0.5m/s、0.7m/s；S2i为夹钳末端在垂直方向上的位移规划曲线，其最大运动速度分别为0.3m/s、0.5m/s、0.7m/s，S1i和S2i共同合成了夹钳末端在平面内的运动。

(a)水平方向

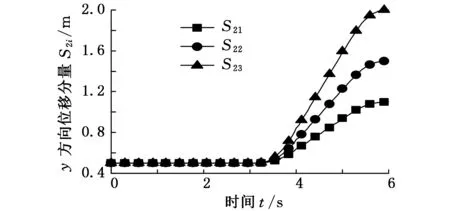
(b)垂直方向图5　夹钳末端在水平和垂直方向的位移分量

5　运动学特性分析

5.1运动学特性数值验证

由机器人的运动空间要求，求解得到机器人机构的结构参数，其相邻铰接点的长度见表2。表3分别给定5组不同的液压缸的长度，根据运动学正解，得到夹钳末端位置的x、y值，见表4。将得到的5组x、y值作为输入进行运动学反解，得到各个液压缸的长度，见表5，经过对比和表3中的值完全一致，证明了运动学正解方程和反解方程的正确性。

表2　重载机器人主要铰接点之间的尺寸

表3　给定液压缸的尺寸　mm

表4　运动学正解结果

表5　运动学反解结果　mm

5.2工作空间分析

全液压锻造重载机器人在空间和平面的运动空间是衡量其实际工作性能的一项重要指标，机器人在平面内的工作空间指当底座旋转角度一定，夹钳末端在运动时的空间包络图。各组液压缸的驱动长度变化范围见表6。

表6　各组驱动缸的长度变化范围　mm

根据运动学正解所得到的夹钳末端位置与三组液压缸驱动尺寸之间的关系函数，采用蒙特卡罗法解析可以得出的机器人的工作空间三维图、O4xz平面、O4xy平面上的投影图和O4xz的截面图分别如图6～图9所示。可知其工作空间大，能够满足工件搬运的作业要求。

图6　工作空间的三维图

图7　O4xz平面投影图

图8　O4xy平面投影图

图9　O4xz平面的截面图

5.3逆运动学分析

针对机器人重载、高速、高精度的特点，且在实际控制中控制器需要实时解算出目标位移时各组缸的位移曲线，为了进一步验证在不同给定的直线位移时各组缸的位移曲线，对机器人进行逆运动学分析。根据参数要求，夹钳末端初始位置坐标为(2500，500)mm，将S1i和S2i作为运动学反解方程中x和y的输入量，在MATLAB中求解后得到各组液压缸的长度变化曲线，如图10～图12所示，其中D1i、 D2i、 D3i(i=1，2，3)分别表示提升缸、提升辅助缸和水平驱动缸在S1i、S2i下的长度变化量。

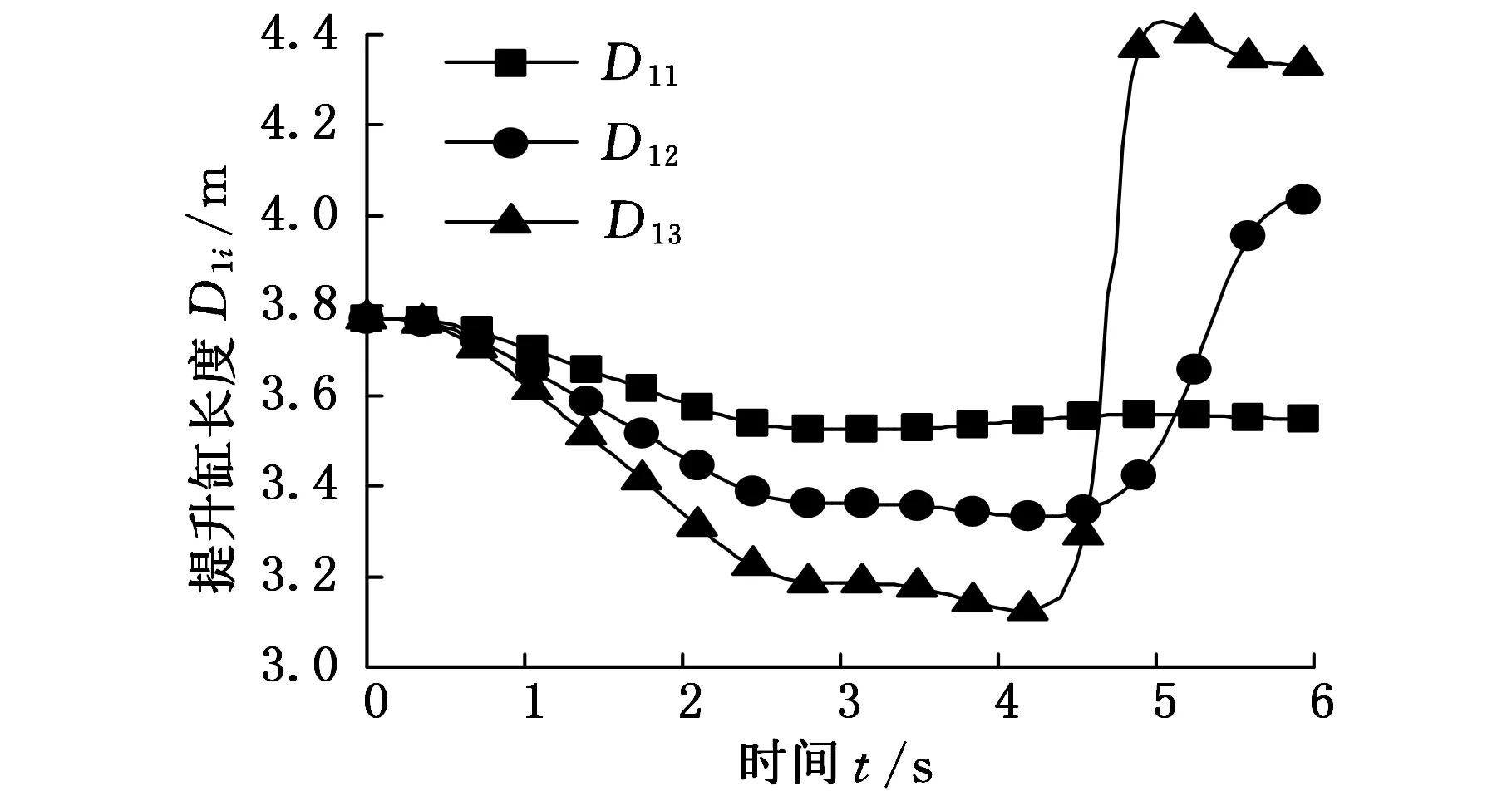
图10　提升缸的长度变化曲线

图11　提升辅助缸的长度变化曲线

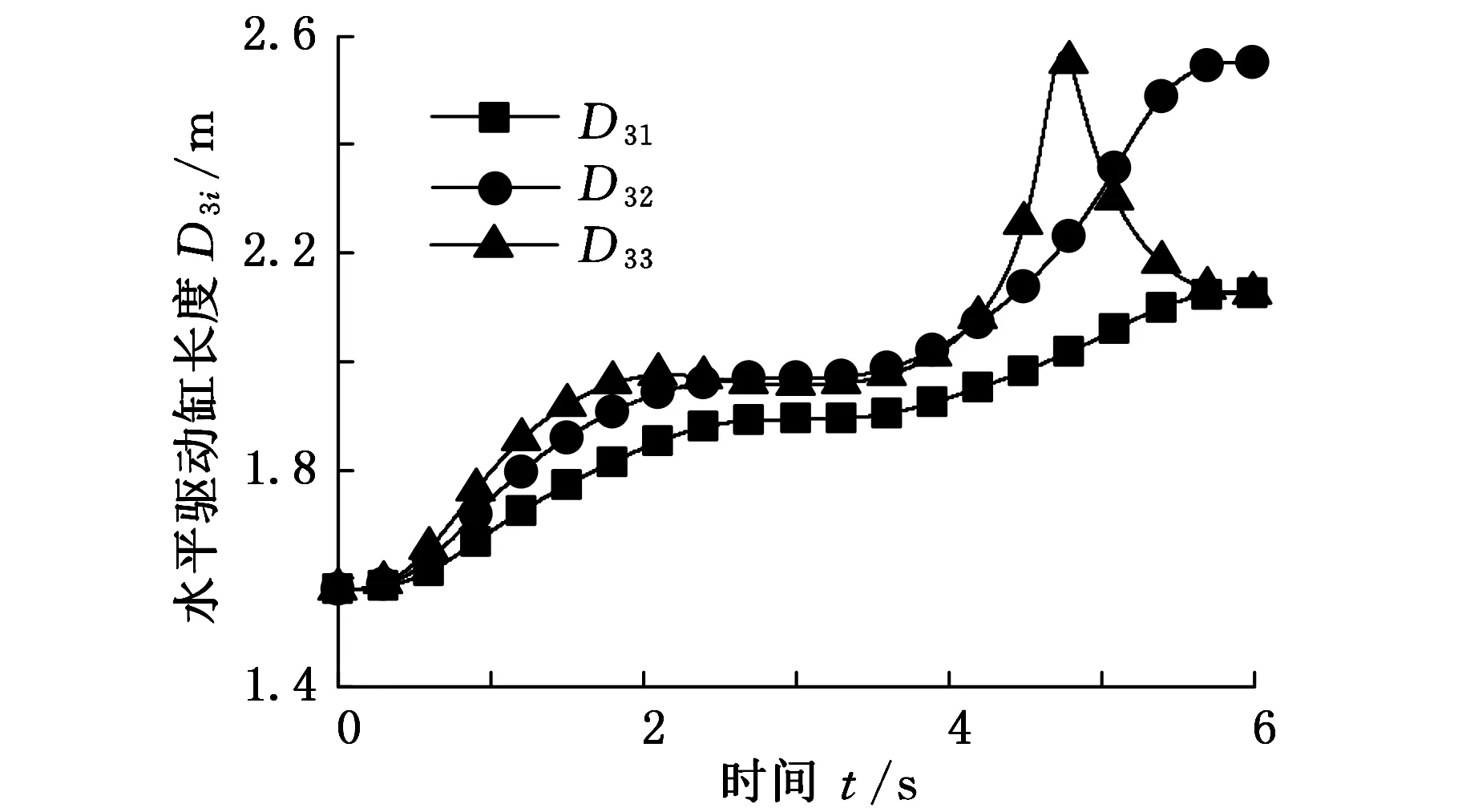
图12　水平驱动缸的长度变化曲线

由图10～图12可以得出，0～3 s内提升缸的长度逐渐减小，提升辅助缸的长度随夹钳的运动逐渐减小，水平驱动缸的长度逐渐增加；3 s时夹钳末端在水平方向的运动结束，然后沿垂直方向进行运动，提升缸和提升辅助缸的长度逐渐增大；在最大速度为0.3 m/s、0.5 m/s的位移规划下，水平驱动缸的长度逐渐增加；在0.7 m/s的位移规划下运动时，水平驱动缸的长度先增大后减小。t为1～2 s和4～5 s时，水平和垂直运动位于匀速运动段，各缸的运动变化曲线也近似为直线，即加速度变化较小，与实际情况相符合。将图10～图12中的曲线与表6中的数据进行比较，各缸的运动范围均在行程之内，仿真结果与实际情况相符合，满足实际要求。

6　动力学特性验证

为了验证机器人的动力学特性，实现在工作过程中对机器人驱动单元的力控制补偿，将表2中各个机构的参数代入动力学特性方程式(13)中，研究在位移规划S1i、S2i时的动力学特性。在MATLAB中搭建动力学模型并进行求解后得出各组缸的驱动力变化曲线，如图13～图15所示，其中，F1i、F2i、F3i(i=1，2，3)分别表示提升缸在S1i、S2i下的驱动力变化曲线。

图13　提升缸的驱动力变化曲线

图14　提升辅助缸的驱动力变化曲线

图15　水平驱动缸的驱动力变化曲线

由图13～图15可以看出，在垂直运动时，提升缸和提升辅助缸的受力要大于水平运动时的受力，这是因为工件在垂直方向有加速度产生，并且提升缸和提升辅助缸主要承受垂直方向的载荷。从曲线的变化趋势来看，各缸驱动力的曲线变化和规划位移下的加速度变化趋势一致，t为0～1 s、2～3 s、3～4 s和5～6 s时，末端的加速度按照正弦曲线进行变化，可以看出此时的力变化曲线也近似为正弦曲线，与加速度变化一致，符合实际情况；t为1～2 s和4～5 s时，曲线的变化趋势相对平缓近似为直线，这是因为此时夹钳末端处于匀速运动阶段，由于杆件之间存在一定的连接和耦合关系，各缸的受力同时发生一定变化，但在匀速运动过程中负载和各个机构的惯性矩和惯性力都很小，故在此过程中各个缸的驱动力变化相对平缓，仿真得到的结果与实际情况符合。

7　结论

(1)提出了一种由三组平行四边形结构构成的重载锻造机器人机构方案，该方案能保证在快速搬运大型重载工件时的可靠性和安全性；机构具有工作空间大、重载下搬运速度快、控制较容易的显著特点。

(2)基于运动闭合矢量法，建立了机构的运动学方程组，采用复数向量法得到了该新型机构的运动学模型，以及该机构的正运动学和逆运动学的解。

(3)基于蒙特卡罗法，分析了机器人的运动空间。对夹钳的路径进行了规划，得到了水平和垂直方向的位移分量，研究了在夹钳保持直线运动时各组液压缸的复合运动情况以及受力情况。

(4)利用虚功原理建立了该新型机构的动力学模型，在MATLAB中求解出夹钳在水平和垂直运动时各个液压缸的驱动力变化曲线，仿真实验与实际情况相符。研究结果为重载锻造机器人的设计提供了一种理论参考。

[1]傅新，徐明，王伟，等．锻造操作机液压系统设计与仿真[J]．机械工程学报，2010，46(11)：49-54．

Fu Xin, Xu Ming, Wang Wei, et al. Hydraulic System Design and Simulation of the Forging Manipulator[J]. Journal of Mechanical Engineering, 2010，46(11)：49-54．

[2]任雷.重载机器人在大型模锻中的应用[C]//第十三届中国国际锻造会议暨2012年全国锻造企业厂长会议.北京，2012:97-99.

[3]高峰,郭为忠,宋清玉,等.重型制造装备国内外研究与发展[J].机械工程学报,2010,46(19):92-107.

Gao Feng, Guo Weizhong, Song Qingyu, et al. Current Development of Heavy-duty Manufacturing Equipments [J]. Journal of Mechanical Engineering, 2010,46(19):92-107.

[4]刘艳妍,杨晋,陈超,等.重载锻造操作机夹持力研究[J].机械工程学报,2012,48(4):66-71.

Liu Yanyan,Yang Jin, Chen Chao, et al. Research of the Chucking Power of the Heavy-loaded Forging Manipulator [J]. Journal of Mechanical Engineering, 2010,46(19):92-107.

[5]郭会光.国内外大锻件制造的发展与对比[J].金属加工(热加工),2014(1):64-68.

Guo Huiguang. Development and Comparison of Large Forgings Manufacturing at China and Abroad[J]. Metal Working,2014(1):64-68.

[6]许允斗,姚建涛,赵永生,等.锻造操作机提升机构设计方法[J].机械工程学报,2012,48(5):28-33.

Xu Yundou, Yao Jiantao, Zhao Yongsheng,et al. Design of Forging Manipulators’s Lifting Mechanism[J]. Journal of Mechanical Engineering, 2012,48(5):28-33.

[7]孙文杰,李刚.基于综合操作性能指标的操作机多目标优化[J].机械工程学报,2014，42(17):52-60.

Sun Wenjie, Li Gang. Multiobjective Optimization for the Forging Manipulator Based on the Comprehensive Manipulation Performance Indices[J]. Journal of Mechanical Engineering, 2014，42(17):52-60.

[8]李阁强,江兵,周斌,等.20T锻造操作机液压控制系统[J].农业机械学报,2015,46(1):352-358.

Li Geqiang, Jiang Bing, Zhou Bin, et al. Hydraulic Control System of 20T Forging Manipulator[J]. Transactions of the Chinese Society for Agricultural Machinery,2015,46(1):352-358.

[9]Tsai L．Robot Analysis：The Mechanics of Serial and Parallel Manipulators[M].New York：John Wiley & Sons，1999．

[10]Cheung，Hung Y S．Modelling and Control of a 2-DOF Planar Parallel Manipulator for Semiconductor Packaging Systems[C]//2005 IEEE/ASME International Conference on Advanced Intelligent Mechatronies. Monterey,2005：717-722．

[11]Lin Y，Song S．A Comparative Study of Inverse Dynamics of Manipulators with Closed-chain Geometry[J]．Journal of Robotic System，1990，7(4)：507-534．

[12]Codourey A．Dynamic Modeling of Parallel Robots for Computed-torque Control Implementation[J]．International Journal of Robotics Research，1998，17(12)：1325-1336．

(编辑陈勇)

Mechanism Design and Analysis of a Novel Hydraulic Driving Heavy Load Forging Robot

Li Geqiang1Wang Shuai1Deng Xiaozhong1Zhou Bin2

1.Henan University of Science and Technology,Luoyang,Henan,471003 2.Anyang Metalforming Machinery Industry Co.,Ltd.,Anyang,Henan,455000

This paper put forward a new mechanism project aiming at the characteristics of large load, fast moving speed and high positioning precision of a hydraulic driving heavy load forging robot. The scheme might realize 5-DOF motion, which contained body walking, body rotation, clamp expansion, clamp lifting, clamp rotation and clamp gripping. The main body of the movement was a kind of hybrid mechanism, which was composed of three groups of parallelogram mechanism, it was driven by three groups of hydraulic cylinders in parallel. This scheme might increase the working space of the robot effectively, making the load allocation reasonable and be easy to control. Kinematics and dynamics model were established, the motion planning of the robot clamp was based on sine curve, the change curves of displacement and driving force of each hydraulic cylinder were obtained in MATLAB. The correctness of the model and the rationality of the mechanism were verified, the scheme provides a solution for the design of heavy load forging robot mechanism.

heavy load forging robot; kinematics; working space; dynamics

TH11；TH13

10.3969/j.issn.1004-132X.2016.09.006

2016-01-11

国家自然科学基金资助项目(51175148)；河南省高等学校重点科研项目(15A460001)

李阁强，男，1971年生。河南科技大学机电工程学院副教授。主要研究方向为机电液一体化技术、流体传动与控制。获省部级一等奖、二等奖各1项。发表论文30余篇。王帅，男，1990年生。河南科技大学机电工程学院硕士研究生。邓效忠，男，1957年生。河南科技大学机电工程学院教授、博士研究生导师。周斌，男，1970年生。安阳锻压机械工业有限公司工程师。