浅埋地下结构抗震设计的反应位移法关键问题

安军海，安林轩，李积栋，陈向红，郭　飞

浅埋地下结构抗震设计的反应位移法关键问题

安军海1，2，安林轩1，2，李积栋3，陈向红1，2，郭飞1，2

（1.北京工业大学建筑工程学院，北京100124；2.北京城市交通协同创新中心，北京100124；3.中国建筑股份有限公司技术中心，北京101300）

为了解决采用反应位移法进行地下结构抗震设计时工程师所面临的不同计算公式和模型的选取及土体是否需要分层等问题，通过具体算例分析，探讨了影响反应位移法计算精度的几个主要因素，具体包括不同规范中推荐的土体相对位移及剪应力的计算公式、土弹簧刚度的确定方法、分层土体与等效单层土体的差异、荷载-结构模型的选择等.研究结果表明:不同方法确定的土体相对位移、剪应力及土弹簧刚度值相差很大，由此造成的结构内力和变形差异显著，推荐公式应谨慎采用；对存在中柱体系的地下结构，荷载-结构模型应优先采用等代框架模型；采用反应位移法计算时，应严格按照实际分层土体完成土层地震响应分析，避免进行等效均一化处理.

反应位移法；地下结构；抗震设计；等代框架

已有震害调查、理论分析及试验研究表明，地下结构在地震作用下随周围土体一起运动，其加速度、位移等结构反应与周围土体基本一致［1-3］.基于地下结构地震响应的特点，20世纪70年代，日本学者提出了地下结构横断面地震反应分析的反应位移法，并成功用于抗震设计［3］.反应位移法因其物理概念明确，计算方法简单，易于为工程师所接受，在抗震领域得到了大范围的推广.

目前，反应位移法的理论与计算不断改进，并在多项工程中得到了应用，已编入我国的一些抗震设计规范，如《城市轨道交通结构抗震设计规范》及《建筑抗震设计规范》［4-5］.在城市地下空间快速发展的背景下，有必要完善地下结构抗震设计方法，确保地下结构具有良好的抗震性能.然而，实际抗震设计中，反应位移法在计算地下结构地震反应时仍存在较大差异，困扰着设计工程师的判断.究其原因，规范中给出的反应位移法的计算模型、地基弹簧系数、土体位移模式及适用范围等尚不够明确［6］.近年来，国内外学者就反应位移法的理论和应用开展了大量研究，往往仅涉及某个计算参数或显著影响因素的改进及对比分析，对地下结构抗震设计中，应用反应位移法时应注意的关键问题缺乏直接有效的指导［3，7-9］.

为了进一步研究反应位移法的实用性，笔者结合具体实例，对其应用于工程实际时的关键问题进行分析，指出反应位移法的误差来源，并给出了使用建议，为地下结构的抗震设计提供参考.

1　反应位移法及其计算步骤

反应位移法的基本思想是地下结构地震时随周围地层一起运动，将地层在地震时产生的沿结构深度方向的相对位移通过地基弹簧以静荷载的形式施加在结构上，同时，考虑地震剪应力和结构惯性力，求得结构由地震引起的附加内力［10-11］.其计算简图如图1所示.

反应位移法计算的主要步骤为:

步骤1对处于自由场的土体进行地震响应分析，或由规范推荐公式计算结构所在土体的相对位移、剪应力及加速度.

步骤2计算出结构的地震惯性力.

步骤3计算描述土-结构相互作用的地基弹簧系数.

步骤4建立地下结构的荷载-结构法模型，将各外荷载施加在模型上，其中惯性力施加在结构重心位置，然后进行地震响应的计算.

为方便起见，施加在地基弹簧远端的土层相对位移往往转化为直接施加在结构上的等效荷载，其转化公式为

式中:p（z）为直接施加在结构上的等效荷载；u（z）、u（zB）分别为距地表面 z处及结构底板处的土体位移.

2　算例设计及计算参数

北京某地铁车站为现浇钢筋混凝土地下双层两跨箱形框架结构，主体结构采用明挖法施工，是由侧墙、梁、板、柱等构件组成，沿车站纵向设置纵梁体系，其中顶板厚0.8 m，中板厚0.4 m，底板厚0.9 m，侧壁厚0.7 m，上柱高5.75 m，下柱高6.25 m，柱子纵向跨度8.1 m，中柱尺寸为1.1 m×0.9 m，结构宽度为19.5 m，高度为14.1 m.

参照地铁车站的设计图纸和地质资料，选取的结构标准断面的形式及土层参数如图2所示，汇总结构的埋深、均一化的场地土特性及地震动特性，其结果见表1.

为了比较反应位移法各因素对计算精度的影响程度，笔者采用人工波作为输入地震动（见图3），对土-地铁车站结构相互作用分析模型（见图4）进行数值模拟，模型上边界取至地表，下边界至等效基岩面（剪切波速≥500 m/s），底面固定，横向边界设置为动力自由场边界，在模型底部水平方向施加加速度荷载，并以计算获得的动力时程分析的结果作为精确解进行比较.

表1　地铁车站结构埋深及场地特性Table 1　Structure buried depths and site features

3　关键计算值的差异性分析

3.1土体相对变形及剪应力

研究表明，土层的相对变形及其对结构周围的剪应力是引起结构内力变化的主要原因，而惯性力对内力计算结果的影响很小，可以忽略不计.目前，抗震设计中，不同抗震设计规范对土层变形及剪应力的计算要求有显著差异，主要由以下几种方法确定:

方法1参照《城市轨道交通结构抗震设计规范》中推荐的经验公式

方法2参照《地下铁道建筑结构抗震设计规范》推荐的经验公式

方法3参照《城市轨道交通工程设计规范》中推荐的经验公式

方法4参照日本的《大型地下结构的抗震设计指南》中推荐的经验公式

方法5基于Shake91或EERA软件的一维土层地震反应求得土体相对位移及剪应力.

基于设计算例，将其相应参数代入公式（1）～（8），同时，应用 EERA软件计划一维土层地震反应，可得到顶板、中板及底板处的土体相对变形和剪应力，如表2所示.其中，相应结构位置处的一维土层反应的监测点布置如图2所示.

从表2可以看出，土层的相对位移随着深度的增加逐渐减少，剪应力则随着深度的增加逐渐增加，反映了土体在地震作用下位移及应力变化的一般规律.

不同方法计算的监测点处的土体相对位移及剪应力差异很大，其中按照方法3的公式计算得到的车站结构顶、底板的相对位移差值最大达到方法5的3倍之多，剪力差别更大，这是由假定不同土体位移模式的计算公式决定的，为分析他们之间的差异对结构内力及变形的影响，表3给出了采用不同计算方法时的结构截面弯矩及层间位移角.

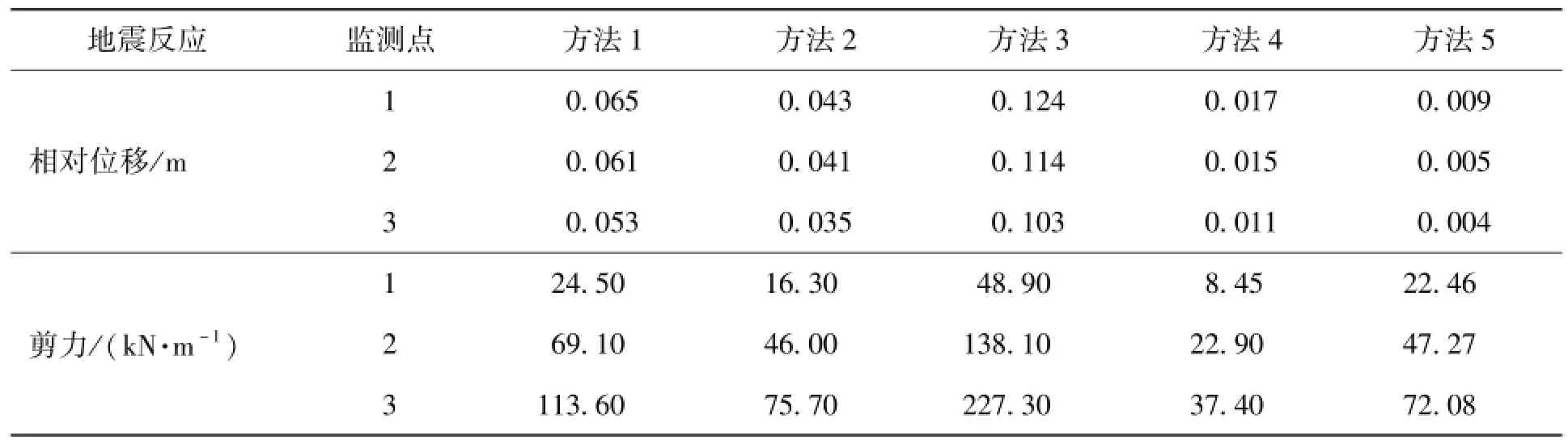
表2　不同方法计算的土体相对位移及剪力Table 2　Soil relative displacement and its shear for different methods

从表3可以看出，与时程分析结果相比，方法1和方法3计算得到的内力和变形值均明显偏大，过于保守；方法4则显著低估了结构的实际内力值，偏于危险，因而方法1、3、4均不适用于该地层工况下的地下结构抗震设计.

方法5（一维土层地震反应）的计算结果整体上与时程分析的结果比较接近，内力的最大误差在8%左右，变形值则更小，用于抗震设计可得到满意的结果.另外，方法2的计算值误差相对也比较小，因此，针对北京地区相似土层的地下结构进行抗震设计时，为方便起见，也可直接采用《城市轨道交通结构抗震设计规范》（征求意见稿2010）中推荐的经验公式.

因此，采用反应位移法进行结构设计时，宜采用一维土层地震反应分析得到的土体相对位移和剪应力值，若直接选用公式进行计算，则应在大量统计分析的基础上得出适合相应地层的公式，并建立起地方标准.

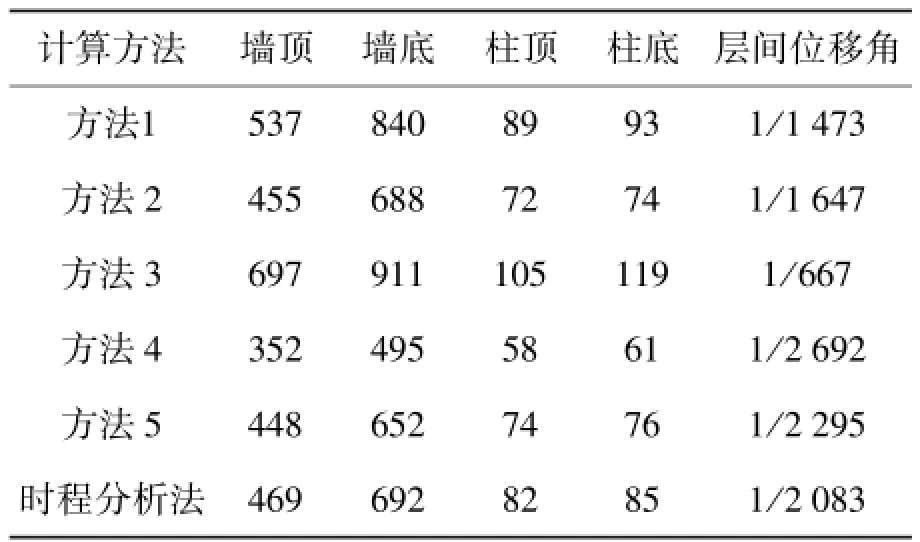
表3　不同方法计算的截面最大弯矩Table 3　Structure maximum moments for different methods　kN·m

3.2土弹簧刚度

应用反应位移法进行地下结构抗震计算时，表征土体与结构之间动力相互作用的土弹簧刚度的准确求解也是关键问题.地基弹簧系数的大小直接影响着土层相对位移引起的等效荷载和周围土层对结构的约束作用，从而影响结构内力的变化.地基弹簧系数的计算公式为

式中:K为地基反力系数；L为地基集中弹簧间距；d为土层沿结构纵向的计算长度.

目前，确定土弹簧刚度值的常用方法主要有以下几种:

方法1国内经验公式法.地基反力系数的计算可采用以下经验公式Kn=3G，Kh=βKn，Kn、Kh分别为土层法向和切向的地基反力系数，也可参照勘察报告中提供的基床系数；G为与地震动最大应变幅值相应的地基土的剪切模量；β为换算系数，其值可取为1/3.该方法操作简单，能考虑不同土层参数的影响，在工程中有一定的应用范围，但对某些特殊地层，求解误差较大.

方法2日本《铁道构造物等设计标准》的经验公式法.规范规定矩形结构的地基弹簧刚度可采用公式

式中:kh为水平基床系数；kv为竖向基床系数；ksv为结构顶底面切向地基弹簧刚度；ksh为结构侧面切向地基弹簧刚度.对于圆形结构，规定地基弹簧刚度的计算公式为

式中G、L、d表示的意义同方法1.

方法3静力有限元法［4］.建立土层有限元模型，将模型底面和侧面固定，去掉结构所在处的土体，在洞口位置的顶面、底面及侧面分别施加竖向均布荷载和水平均布荷载q，得到不同荷载作用相应的变形值δ，进而计算出地基反力系数K=q/δ，具体计算过程如图5所示，其中有限元网格单元尺寸取为2 m.

为比较土弹簧刚度计算公式的差异性，基于设计算例，表4给出了采用不同计算方法时得到的在结构顶面及侧面的土体切向和法向弹簧刚度值.

从表中可以看出，与有限元法相比，国内公式整体上过高估计了土层的弹簧刚度，某些部位的弹簧刚度值甚至超出10倍以上；日本公式的计算值有些低估了土弹簧刚度，但整体上与有限元法的计算值比较接近.

表4　不同方法计算的土弹簧刚度Table 4　Soil spring stiffness for different methods　MN/m

基于表4的土弹簧刚度值，建立设计算例的荷载-结构模型，得到不同方法计算的结构截面最大弯矩值，并以时程分析的计算值作为精确解进行比较，其结果见表5.

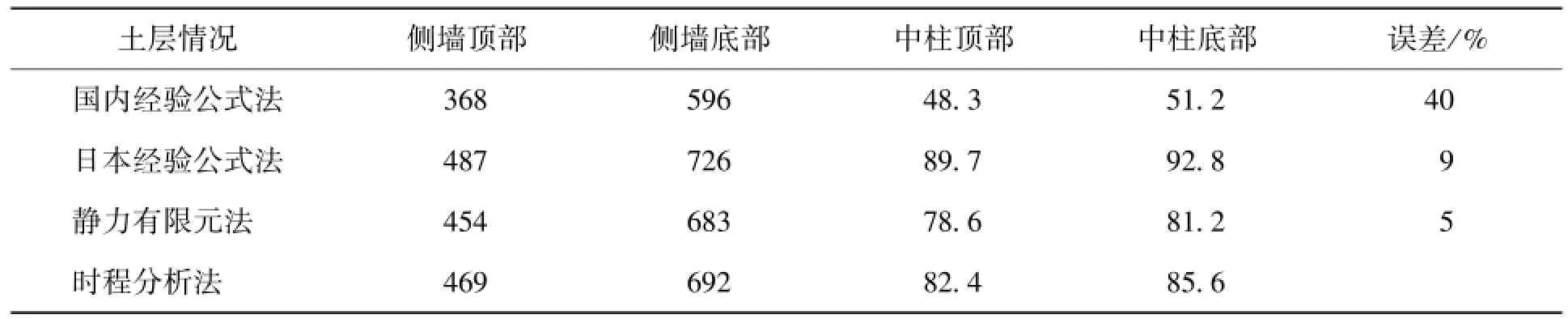
表5　不同方法计算的截面最大弯矩Table 5　Structure maximum moments for different methods　kN·m

从表中可以看出，与时程分析的结果相比，国内经验公式计算得到的结构内力值因地基弹簧系数偏大而明显偏小，最大误差可达40%左右，用于结构设计偏于危险；日本经验公式的计算值整体上有所偏大，最大误差接近10%，用于结构设计偏于保守；而有限元法的计算结果与时程分析法吻合较好，误差可控制在5%以内，可用于地下结构的抗震计算.但结构高度较大时，有限元法计算的土弹簧系数往往仍沿深度方向上取一个定值，与实际土层条件不很相符，这时可能会造成较大误差.

3.3单层与分层土体

等效匀质单层土体是将结构所在土层的水平和垂直基床系数、土体容重等参数进行加权平均，并将其转化为土层弹簧刚度施加在模型上，再按照一维土层地震反应得到的相对位移和剪力，基于“延米框架”模型，求出其内力值.为了给工程师进行抗震设计时所要选取的土体模式提供参考，本文比较分析了实际分层土体和等效单层土体在结构内力计算结果上的差异程度.表6给出了结构侧墙部位的等效匀质单一土层和分层土的弹簧刚度值及容重，并基于设计算例得到了其相应的弯矩最大值，见表7.

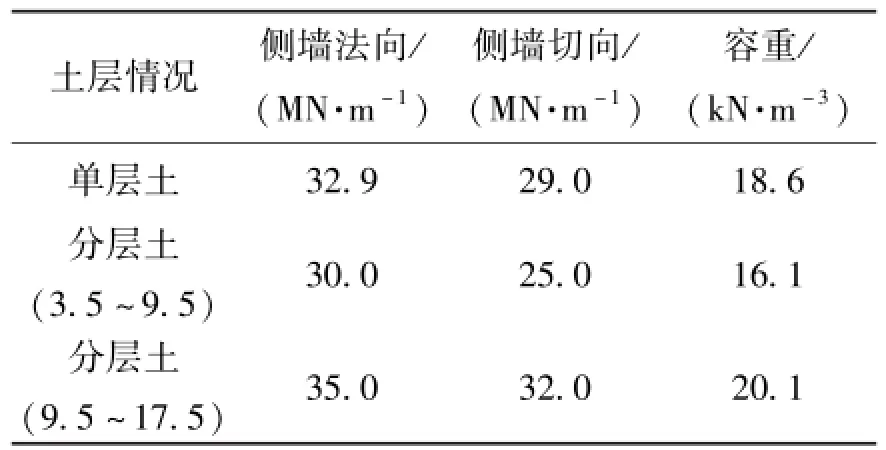
表6　分层土与单层土模型时土弹簧刚度及容重Table 6　Structure maximum moments and bulk density for layered soil model and uniform soil

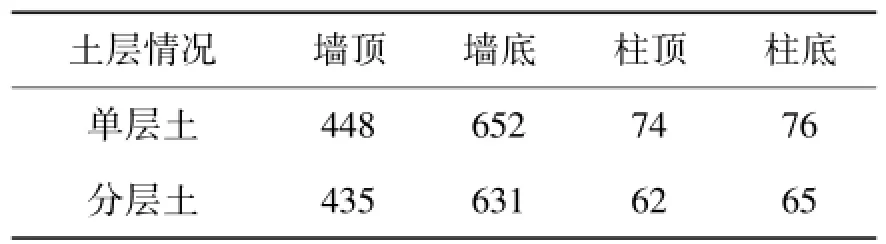
表7　分层土与单层土模型时截面最大弯矩Table 7　Structure maximum moments for different methods　kN·m

从表7中可以看出，单层土模型工况下的结构最大内力值要大于分层土的，即分层土模型对结构的约束作用更大，对分层土进行等效均一化实际上降低了其对结构的限制，从而产生误差，若分层土之间的土性差别较大，会造成更大误差，因此，实际工程中应尽量避免将实际分层土等效简化为匀质单层土.

3.4计算模型

已有研究表明，采用反应位移法进行地下结构横断面的抗震计算时，不同计算模型引起的误差不同，有时差异还比较大，甚至出现有些关键构件的内力失真.目前，计算结构内力的反应位移法模型主要有以下几种:

方法1平面模型.抗震设计规范（GB）一般推荐采用的荷载-结构模型是“延米框架”模型，模型假定结构某主轴方向的抗侧力构件仅承担该方向的地震作用，其惯例做法是取纵向1 m，中柱按照压缩刚度或抗弯刚度相等的原则等效为一面连续薄墙.

方法2等代框架模型.《城市轨道交通工程设计规范》（DB）针对存在纵梁-柱体系的地下结构，推荐采用等代框架模型，模型要求中柱按真实截面尺寸建模，结构的墙板构件截面宽度取标准断面纵梁的一个跨度长.

为比较不同简化分析模型计算结构内力的精确程度，基于设计算例，给出选取不同模型时结构截面的最大弯矩值，见表8.

表8　不同简化模型时截面最大弯矩及误差Table 8　Structure maximum moments and error for different simplified models　kN·m

从表中可以看出，与时程分析结果相比，“等代框架模型”计算出的结构内力值偏大，“延米框架模型”计算的内力值偏小，二者在侧墙部位的误差均在5%左右，均在可接受的范围之内，但对于中柱部位的内力，“延米框架模型”的计算结果明显偏小，最大误差达到16%，而中柱又是地下结构抗震设计的薄弱部位，以此进行配筋计算，偏于危险.采用“等代框架模型”计算的中柱内力误差在5%以内，与精确解非常接近，用于结构抗震设计更为合理.

因此，实际工程中，对无中柱体系的地下结构，“延米框架”和“等代框架”模型均可选用，而对存在中柱体系的地下结构，推荐采用“等代框架”模型进行地震工况的内力计算.

4　结论

反应位移法是目前地下结构抗震设计普遍采用的分析方法，本文针对工程应用实际，采用对比分析的方法，以时程分析的结果作为精确方法进行比较，探讨了影响其计算精度的主要因素，得到以下主要结论:

1）不同规范推荐的位移和剪力公式计算结果明显不同，将其作为荷载施加在结构上，使得结构内力差异很大，用于设计或偏于保守，或偏于危险，因而，应谨慎使用，推荐采用一维土层地震反应分析的计算结果.

2）地基弹簧刚度的计算中，推荐采用有限元法或日本经验公式法，其计算精度良好，国内规范经验公式的计算结果误差较大.

3）应用反应位移法进行内力计算时，不能将实际分层土体进行等效均一化，应根据实际土层情况进行自由场的地震反应分析.

4）对无中柱体系的地下结构，抗震计算时可任选“延米框架”和“等代框架”模型，而对存在中柱体系的地下结构，应采用“等代框架”模型.

［1］CHEN G X，ZHUANG H Y，LIU W Q，et al.Analysis on the earthquake response of subway station based on the sub-structuring subtraction method［J］.Journal of Disaster Prevention and Mitigation Engineering，2004，24（4）: 195-199.

［2］袁勇，禹海涛，陈之毅.软土浅埋框架结构抗震计算方法评价［J］.振动与冲击，2009，28（8）:50-56.

YUAN Y，YU H T，CHEN Z Y.Evaluation of seismic calculation methods for shallow-buried frame structures in soft soil［J］.Journal of Vibration and Shock，2009，28（8）:50-56.（in Chinese）

［3］川岛一彦.地下构筑物瘴耐震设计［M］.日本:鹿岛出版会，l994:43-60.

［4］中华人民共和国国家标准编写组.城市轨道交通结构抗震设计规范:GB50909—2014［S］.北京:中国计划出版社，2014.

［5］中华人民共和国国家标准编写组.建筑抗震设计规范: GB50011—2010［S］.北京:中国建筑工业出版社，2010.

［6］刘晶波，王文晖，张小波，等.地下结构横断面地震反应分析的反应位移法研究［J］.岩石力学与工程学报，2013，32（1）:161-167.

LIU J B，WANG W H，ZHANG X B，et al.Research on responsedeformationmethodinseismicanalysisof undergroundstructure［J］.ChineseJournalofRock Mechanics and Engineering，2013，32（1）:161-167.（in Chinese）

［7］王文沛，陶连金，张波，等.基于薄层分析的反应位移法研究［J］.北京工业大学学报，2012，38（8）:1231-1235.

WANG W P，TAO L J，ZHANG B，et al.Displacement response method based on thin layer method［J］.Journal of Beijing University of Technology，2012，38（8）:1231-1235.（in Chinese）

［8］王国波，王敏，覃程，等.对反应位移法中几个关键问题的探讨［J］.地下空间与工程学报，2014，10（6）: 1367-1371.

WANG G B，WANG M，QIN C，et al.Investigation on several key issues of response displacement method［J］. Chinese Journal of Underground Space and Engineering，2014，10（6）:1367-1371.（in Chinese）

［9］李亮，杨晓慧，杜修力.地下结构地震反应计算的改进的反应位移法［J］.岩土工程学报，2014，36（7）: 1360-1364.

LI L，YANG X H，DU X L.Improved response displacement method for evaluating seismic responses of underground structures［J］.Chinese Journal of Geotechnical Engineering，2014，36（7）:1360-1364.（in Chinese）

［10］董正方，王君杰，王文彪，等.基于土层位移差的地下结构抗震反应位移法分析［J］.振动与冲击，2013，32（7）:38-42.

DONG Z F，WANG J J，WANG W B，et al.Response displacement method for seismic analysis of underground structures based on soil layers displacement difference［J］.Journal of Vibration and Shock，2013，32（7）:38-42.（in Chinese）

［11］王朝晖，汪梦甫.双向水平地震作用下非对称框架结构抗震分析简化方法［J］.湖南大学学报（自然科学版），2007，34（4）:1-4.

LIU C H，WANG M F.Simplified procedure for the seismic analysis of asymmetric frame structures subject to two-directional horizontal earthquake［J］.Journal of Hunan University（Natural Sciences），2007，34（4）:1-4.（in Chinese）

（责任编辑郑筱梅）

Response Displacement Method in Several Key Issues of Shallow Buried Underground Structure Seismic Design

AN Junhai1，2，AN Linxuan1，2，LI Jidong3，CHEN Xianghong1，2，GUO Fei1，2
（1.College of Architecture and Civil Engineering，Beijing University of Technology，Beijing 100124，China；2.Center of Cooperative Innovation for Beijing Metropolitan Transportation，Beijing 100124，China；3.China State Construction Technical Center，Beijing 101300，China）

In order to solve problems of selection of different formulas，calculation model as well as whether need to be decorated in layered soil and so on，in view of actual engineering applications，several main factors affecting the calculation accuracy of response displacement method were discussed based on some specific examples in this paper.The examples include different calculation formulas for relative displacement of soil and shear stress recommended by codes，different methods for soil spring stiffness determination，the differences between equivalent single layer soil and actual layered soil，and the choice of load-structure models.The results show that there are large differences on soil relative displacement，shear stress and soil spring stiffness that calculated by different methods，which can cause remarkably differences in structure's internal force and deformation.Recommended formula should be carefully used.In situation of an underground structure with beam-column system，the equivalent planar frame model should be adopted firstly.Additionally，the actual layered soil should be used to complete the soil seismic response analysis when the response displacement method is employed.

response displacement method；underground structure；aseismic design；equivalent planar frame model

TU 311.3；U 231

A

0254-0037（2016）06-0926-07

10.11936/bjutxb2015080015

2015-08-05

国家自然科学基金资助项目（90715035，41272337，51421005）

安军海（1987—），男，博士研究生，主要从事地下结构抗震方面的研究，E-mail:tsanjunhai@126.com