矩震级及震源机制相似地震的辐射能量差别
——2014年鲁甸地震与景谷地震宽频带体波震级的比较

2016-09-04 02:30宋潇潇吴忠良蒋长胜李佳威

中国地震 2016年4期

宋潇潇吴忠良蒋长胜李佳威

1）中国地震局地球物理研究所，北京市民族大学南路5号 100081

2）湖北省地震局，武汉市武昌区洪山侧路40号 430071

0 引言

2014年8月 3日云南鲁甸MS6.5（MW6.2）地震中有 700人死亡或失踪、约 3000人受伤①http：//www.cea.gov.cn/publish/dizhenj/468/553/100821/100826/20140807212938960445806/index.html。与此对照，2014年10月7日云南景谷MS6.6（MW6.1）地震中有1人死亡、约300人受伤②http：//www.cea.gov.cn/publish/dizhenj/468/553/101360/101364/20141009091722022145593/index.html。这两次地震的震源机制和矩震级、面波震级均相近。对鲁甸地震灾害偏重的成因，已有多方面讨论，Cheng等（2015）认为鲁甸地震灾害主要是因当地建筑的易损性以及地震诱发的滑坡等所致。但同时有限的强震记录也显示，鲁甸地震的震源谱确比景谷地震具有更多的高频成分。赵仲和（2014）援引IRIS震源参数测定结果认为，鲁甸地震辐射能量的高频成分较景谷地震更为丰富。张广伟等（2014）通过地震序列重新定位及震源机制的研究认为，鲁甸地震的矩心相对于破裂起始点较浅，从而导致灾害严重。许力生等（2014）基于鲁甸地震不同方位台站上的视震源时间函数，认为地震能量的集中释放可能是造成灾害的主要原因。

鲁甸地震与景谷地震所造成灾害的差别，决非单一因素所致。从地震学角度而言，两次地震辐射能量的差别及其致灾效果值得研究。历史上，曾有若干矩震级相近但辐射能量不同，从而造成不同灾害的震例（Choy et al，2001、2009）。本文试图通过（累积）宽频带体波震级讨论这一问题。

用宽频带体波震级描述地震辐射能量（Bormann et al，2008、2011、2012），既是传统的体波震级概念的推广，又是测定过程较为复杂的辐射能量（Boatwright et al，1986、2002；Choy et al，1997；Pulido et al，2000；Izutani et al，2001）的一种简便的近似。对于大地震和巨大地震，一般以“累积宽频带体波震级”来克服其“饱和”的缺点（Bormann et al，1975、2005、2006）。对于中等地震，累积宽频带体波震级mBc则“退化”为通常的宽频带体波震级mB。

1 累积宽频带体波震级m Bc

按照Bormann等（2005、2009）的研究，累积宽频带体波震级mBc由

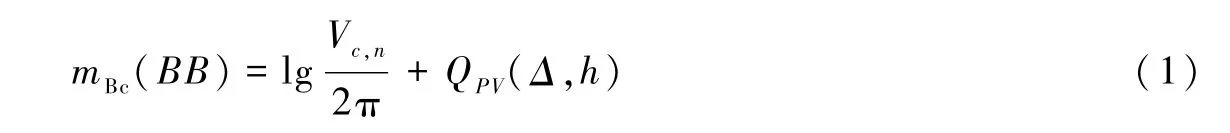
给出。其中

Vi表示宽频带速度记录垂直分量上前n个“子事件”（subevent）的速度峰值，QPV（Δ，h）为量规函数。

此处“子事件”的概念，与震源过程中的“子事件”有一定联系，但并不完全等同。从地震波形分析的角度，Bormann等（2009）将“子事件”定义为：从P波到时开始，找到波形与零轴每2个交点间绝对值最大的振幅，对每个绝对值最大的振幅，若其大于此前P波波列中出现的绝对值最大振幅的q倍，则将其定义为一次“子事件”，即

q值经验地取为0.6。通常计算累积宽频带体波震级的时间窗长度与地震的震源时间函数的长度相当，同时对于任何事件，求和时间窗都在S波到达前终止（Bormann et al，2009），因此，对于震源时间函数较短的中等地震，累积宽频带体波震级自然地“退化”为通常的宽频带体波震级。

本文所用量规函数取自Saul等（2007）的结果，Saul等（2007）根据1200个地震事件、约120000个宽频带体波震级mB的测定结果，修改了Gutenberg等（1956）的量规函数。该量规函数适用于震中距为6°～103°的范围。图1给出了Saul等（2007）的量规函数，同时作为对照，也给出了中国地震震级测定标准规定的量规函数（中华人民共和国国家标准，2016）。

2 所用数据和m Bc的测定

本文所用地震波形数据包括鲁甸地震、景谷地震震中距6°～80°范围内的地震台站的垂直分量波形记录，均来自国家测震台网数据备份中心③郑秀芬、姚志祥、杨辉等，2007，国家测震台网地震波形数据，中国地震局地球物理研究所国家地震信息服务数据中心，doi：10.11998/SEIS＿DMC.Seismic.China＿Network.2007.01.v1。和IRIS数据中心。除去台站记录不正常的数据、P波初至不清晰的波形、记录信噪比小于2的波形，同时尽可能考虑不同震中距和方位角上的均匀分布，得到142个台站记录的鲁甸地震和138个台站记录的景谷地震的地震波形，台站分布如图2所示。

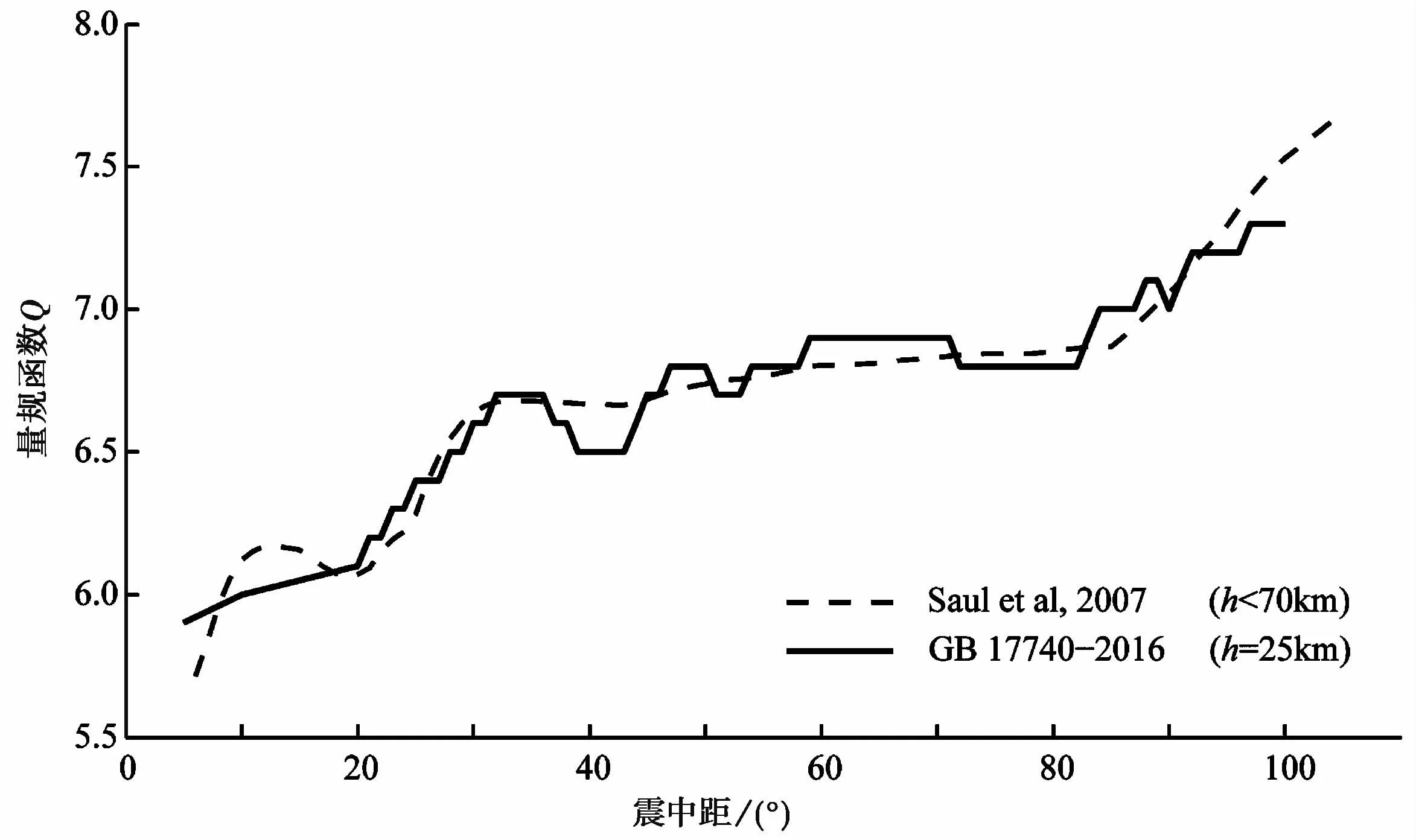
图1 Saul等（2007）的宽频带体波震级量规函数（虚线）与中国地震震级测定标准规定的垂直向P波体波震级量规函数（实线）

图2 提供波形资料的台站分布

波形的预处理包括去平均、去倾斜、利用仪器响应文件中的灵敏度将记录的数字数（counts）转换成以μm/s为单位的地动速度（刘瑞丰等，2015b）等。按式（3）所定义的“子事件”概念，找出波形在规定时间窗口内所有满足条件的速度峰值Vi，再依据公式（1）和（2），按台站震中距所对应的量规函数Q值进行校正，得到每个台所测得的mBc。

图3给出了NM.ARS和XJ.YUT两个台站的鲁甸地震和景谷地震的mBc的计算过程。黑色实线为预处理后的地震波形，蓝色竖线为所识别出的“子事件”的位置，红色阶梯状实线表示mBc随时间的变化。由图3可见，XJ.YUT台记录的景谷地震的“子事件”主要集中在P波后约10s以内，而NM.ARS台记录的鲁甸地震的“子事件”持续时间则较长。图中蓝色和红色三角分别标出了P～S波段最大振幅处的mBc值和高频P波能量包络（灰色阴影部分）下降至峰值的40%时的mBc值。高频P波的包络线通过对宽频带速度记录的高频P波的平方作滑动平均处理得到，滤波频段取为 1～3Hz，平滑窗长为 5s（Hara，2007；Bormann et al，2008）。

图3 震级 m Bc的测定过程。（a）鲁甸地震（NM.ARS台），（b）景谷地震（XJ.YUT台）

远震范围内的大地震，其震源时间函数持续时间较长，远大于P波组（P＋pP＋sP）中各震相的到时差，因此高频P波的包络可近似看作大地震的震源时间函数。然而对于中等地震，这一包络已不再对应具有确定物理意义的震源时间函数，相应地，根据式（3）所识别出的“子事件”也不能简单地与震源过程中的“子事件”进行直接类比。鲁甸地震与景谷地震的“子事件”持续时间的差别，可能有两个原因，一是鲁甸地震具有更为复杂的震源过程，二是鲁甸地震震源区的复杂结构，使鲁甸地震的能量释放，通过反射和折射等形成了后续的能量。

3 两次地震的m Bc测定结果及其比较

图4给出了所测得的累积宽频带体波震级mBc与震中距的关系。由图4可见，总体而言，鲁甸地震的mBc（红色圆点）高于景谷地震（蓝色方块）。为了更清楚地考察这种差别随震中距的变化，图5将震中距以5°或10°步长分成10个区间，并分别计算了每一区间的mBc的平均值和标准差。值得指出的是，由于震级可以看成是能量的指数，因此简单地对震级求算术平均并不恰当。这里的平均值和标准差，仅是为了更直观地表示两次地震的震级差别及其随震中距的变化。

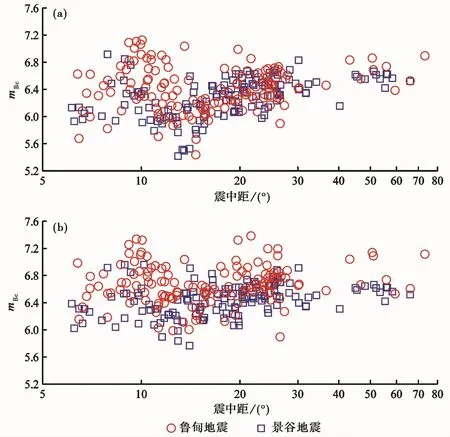
图4 m Bc随震中距的变化（横坐标采用对数坐标）

从图4、图5可见，当用较短的波形（10s）计算mBc时，两次地震在震中距6°～15°范围内存在明显差异；对于震中距更大的台站，这种差别不复显现。一种可能的解释是，鲁甸地震的高频辐射，对两次地震的辐射能量的差别具有决定性的贡献，高频辐射成分随着震中矩的增加而衰减，因此在震中距更大时，宽频带体波震级的差别不再明显。另一方面，若将时间窗取至20s，则所有震中距范围内的宽频带体波震级差都十分明显，说明对两次地震的辐射能量的差别的贡献，不仅来自震源时间函数的高频成分，而且来自由于震源区复杂结构而形成的后续能量。

由于Saul等（2007）的量规函数与中国地震震级测定标准规定的量规函数（中华人民共和国国家标准，2016）存在差别，并且这种差别在震中距6°～15°范围内更为明显，作为对照，图6给出了使用中国地震震级测定标准规定的量规函数（中华人民共和国国家标准，2016）的结果，由图6可见两个量规函数的差别并不影响两次地震的宽频带体波震级差。

图5 用误差棒给出按震中距分段求得的m Bc平均值和标准差

图6 用误差棒给出采用中国地震震级测定标准规定的体波震级量规函数求得的m Bc的平均值和标准差

图7给出了各台站mBc值的方位分布。由图可见，对10s时间窗的结果，鲁甸地震的震级偏大的台站（在图7中，mBc≥6.8的台站），集中分布在NW-SE方向上，这与此次地震的震源破裂传播方向（张勇等，2014；许力生等，2014）是一致的。对20s时间窗的结果，震级偏大的台站也集中分布在NW-SE方向上，一种可能的解释是NW-SE向展布的地震断层带中形成的导波对形成后续的能量具有重要作用。

4 结论和讨论

宽频带体波震级mBc是对地震辐射能量的一种描述。本文的结果表明，鲁甸地震的mBc高于景谷地震，就是说，在导致两次地震灾害差别较大的诸多因素中，地震辐射能量的差别具有不可忽视的作用。作为对照，表1给出了IRIS网站公布的鲁甸地震④IRIS DMC，2013a，Data Services Products：EQ Energy Earthquake energy＆rupture duration，doi：10.17611/DP/9633579.和景谷地震⑤IRISDMC，2013b，Data Services Products：EQ Energy Earthquake energy＆rupture duration，doi：10.17611/DP/9712498.的能量震级测定结果（http：//ds.iris.eduspudeqenergy），相应的结果是对震中距 25°～80°的远震范围内的宽频带（0.5～70.0s）和高频（0.5～2.0s）地震记录的垂直分量P波组测得的，以宽频带辐射能量震级Me（BB）和高频辐射能量震级Me（HF）来表示（Choy et al，1995；Convers et al，2011）。可见两次地震的宽频带辐射能量震级和高频辐射能量震级的差，与本文得到的（累积）宽频带体波震级的差在数量上相当。从表1还可以看出，矩震级接近的鲁甸地震与景谷地震具有不同的能量震级，Me鲁甸地震的能量震级高于景谷地震，其中高频能量震级的差又略高于宽频带能量震级的差，说明鲁甸地震的高频成分较景谷地震更为丰富，这个结论，也与本文的结果吻合。

图7 测得的m Bc的方位分布

本文进一步推测，鲁甸地震的偏高的辐射能量，首先来自震源函数中显著的高频成分。由图7推测，这些高频成分既来自震源凹凸体造成的高频辐射，同时也（更主要地）来自地震破裂传播的多普勒效应。对鲁甸地震破裂过程的研究（张勇等，2014；戴嘉伟等，2015；许冲，2015）表明，此次地震的明显特征是自下而上、自NW向SE方向传播，并在SE端穿透地表。另一方面，从图3、4、5可以看出，不仅鲁甸地震本身所具有的高频成分，而且由鲁甸地震震源区的复杂结构（最可能的是地震断层带）所形成的后续能量，都对两次地震辐射能量的差别有重要贡献。

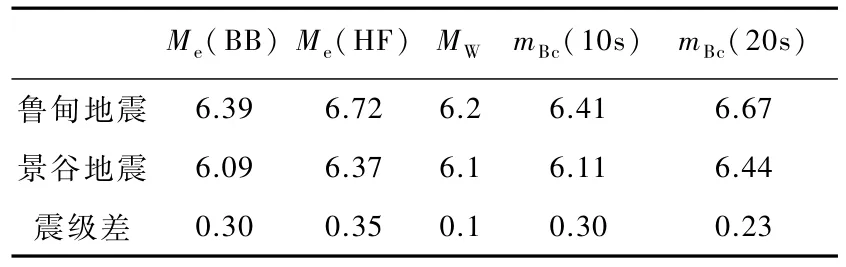
表1 IRIS公布的能量震级M e、GCMT给出的矩震级M W及由前10s和20s波形给出的m Bc

矩震级相近但辐射能量不同，从而造成灾害不同的震例（Choy et al，2001、2009）在地震研究中具有不可忽视的重要意义。一般说来，不同震源机制类型的地震，其能量与地震矩之比（有时称为折合能量）本来就是不同的（Wyss et al，1968；Wu，2001）。鲁甸地震和景谷地震的特殊之处在于，它们不但矩震级相近，而且震源机制也相近，都是近直立的走滑型断层，从这个意义上讲，这两次地震提供了进行这种比较的更为典型的震例。

在我国的震级测定中（中国地震局，2001；刘瑞丰等，2015a；中华人民共和国国家标准，2016），目前（累积）宽频带体波震级mBc尚未用于地震观测与解释的常规工作中。通常，对于地震速报和地震应急而言，测出单一的震级，足以给出有用的信息。然而从鲁甸地震和景谷地震的比较可知，不同的震级，因其所代表的物理意义不同，在地震应急救援和地震研究中，具有不能彼此取代的作用。而从地震灾害的角度看，代表辐射能量的（累积）宽频带体波震级，甚至比面波震级和矩震级具有更为直接的减灾意义。因此可以期待这一震级成为中国地震监测中的常规测定震级。