巧用“体验感悟”培养数学推理能力

文/王斐斐

巧用“体验感悟”培养数学推理能力

文/王斐斐

《义务教育数学课程标准》（2011年版）指出：“推理能力的发展应贯穿在整个数学学习过程中。推理是数学的基本思维方式，也是人们在学习和生活中经常使用的思维方式。教师在教学过程中，应该设计适当的学习活动，引导学生通过观察、实验、猜想、验证等活动发现一些规律，猜测某些结论，发展合情推理能力，能进行有条理的思考。”由此可见，推理能力的培养是一个体验、探索的“再创造”过程，它要求的是学生在知识的积累与自主参与的学习过程中，“悟”出一些道理、规律和方法。因此，推理能力只有让学生在学习的过程中充分体验、感悟，才能得以培养和形成。

解读教材，思之有“源”，让推理有迹可循

等量代换是数学中一种基本的思想方法，也是代数思想方法的基础，山东青岛版教材在小学三年级上册58-59的“智慧广场”中第一次出现等量代换。教材是用学生熟悉的图形呈现问题，尊重了儿童从直观到抽象的认知特点，并为学生呈现了四种解决问题的方法。前两种都是利用学生已有的知识基础，用列举的方法自主尝试寻找答案，他们可以从第一个信息入手，凭经验列举，直到找到符合第二个信息的答案，当然也可以从第二个信息入手，有序列举，直到找出符合信息的答案。紧接着，教材抛出了“能把‘三角’换成‘圆圈’来试一试吗”这个问题，一下子提升了学生的思维层次，学生在观察、思考、推理的过程中，体验到根据三角形和圆圈之间的关系进行代换，领悟到用等量代换的方法解决问题更为简单、巧妙，从而理解这一重要的数学思想方法。

教材的编排，也巧妙地引导了学生自主探索、获得新知的过程，在与列举思想方法的对比中初步体验等量代换的思想方法的价值。整个学习过程就是让学生经历一个“无序——有序——优化”的过程，而在这个过程中对数学发展影响最大的三个重要思想之一“推理能力的培养”，已经成为主宰这节课的关键。因此充分进行体验感悟，进一步提升学生的推理能力就成为本节课所承载的一项重要目标。

操作体验，推之有“据”，让推理走向明朗

“只是告诉我，我会忘记；要是演示给我，我就会记住；如果还让我参与其中，我就会明白。”可见，让学生动手操作体验，并在观察、实验、证明中进一步感悟，利于发展学生推理的能力。为此，笔者设计了这样的环节：

谈话：还有其他的方法吗？能把“三角”换成“圆圈”试一试吗？

文字叙述法：1个“三角”加1个“圆圈”等于12，1个“三角”等于3个“圆圈”，相当于4个“圆圈”等于12，1个“圆圈”等于3。

画图演示法：

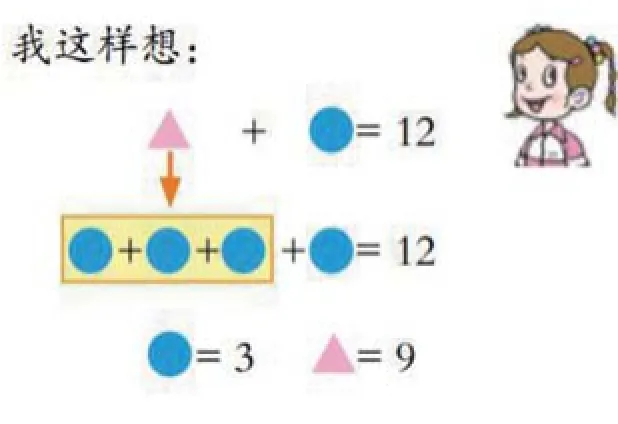
谈话：为什么可以用三个“圆圈”代换一个“三角”？这样代换的好处是什么？请你把答案带回信息中去验证一下。

首先，让学生仔细分析圆形和三角形的关系，让他们通过自主观察发现1个“三角”加1个“圆圈”等于12，1个“三角”是一个“圆圈”的3倍，并找到一个“三角”等于3个“圆圈”这一等量关系，为后面学生“换一换”打下基础；其次，为学生准备充分的学具（圆片、三角形片、答题卡等），把课堂还给学生，让学生有充足的时间动手操作。学生通过有“据”推理，根据1个“三角”等于3个“圆圈”这一等量关系，推理得到三个圆形就可以替换一个三角形，让推理走向明朗。通过动手画图，把等量代换这个抽象的数学思想方法变为学生自己可以感受的形式呈现，然后内化为自己的认识，当学生能画出自己理解的示意图时，问题也就基本解决了。也可以用学具摆一摆、换一换，通过想、画、看、理解等量代换法，有“据”推理，操作体验，体会等量代换法的核心即找到等量关系进行代换。学生在画一画、摆一摆的基础上，明白了1个“三角”加一个“圆圈”等于12，1个“三角”可以用3个“圆圈”替换，那么这个等式就可以变成4个“圆圈”相加等于12，求一个圆形就用12除以4等于3，并且清楚地说出算式中的“4”就表示四个圆形。最后笔者再引导孩子把结果带回到信息中进行验证，总结等量代换的方法。就这样让孩子们经历了猜想、操作、验证的过程体验，在一次次的体验中提高思维水平，理解基本概念，推理能力也有了进一步的提升。

生活体验，悟之有“道”，让推理鲜活灵动

“数学来源于生活”，知识点在生活中基本都能找到原型。在学生学会用等量代换的方法解决问题后，笔者设计了曹冲称象的故事，让学生体会故事中等量代换的思想。

教师：同学们，你们听过“曹冲称象”的故事吗？（播放曹冲称象的片段）为什么曹冲称出了石头的重量也就知道了大象的重量？

学生：因为石头的重量和大象的重量是相等的。

学生有了初步的推理，可以把称大象换成称石头。因为石头的重量和大象的重量相等，用石头“代替”大象，即用一种量可以代换和它相等的另一种量。此刻，笔者又进行了追问：“只能用同等重量的石头替换吗？用同等重量的沙子可不可以？用我们班的小朋友呢？”通过启发孩子们进一步的思考让大家认识到只要是同等重量的物品就可以互相替换，在这里孩子们对只有“等量”才能“代换”有了鲜活灵动的感悟。

数学的学习过程是把现实问题转化为数学问题的过程。任何一名学生，即使是刚入学的一年级新同学，对数学的一些知识也并不是一无所知，无论是生活经验还是数学的基础知识，他们脑中都有一些自己的理解，只不过没有那么准确。因此，教师要给学生充分的时间和充足的资料，让孩子们去经历，去体验，去理解，把现实与抽象的数学概念联系起来，悟出其中的道理。

应用体验，用之有“优”，让推理自觉应用

学习数学的最终目的是回归生活应用。把生活中的问题转变为数学的问题，用数学方法巧妙解决，这就需要学生具有这种数学能力，而这种能力就需要教师去培养。因此，青岛版教材在练习设计上从学生的实际生活中找素材，让学生体验到生活中处处有数学，处处用数学。

谈话：你会用代换法了吗？想不想试试解决生活中的问题？

学生自主解决，并清楚地说出解决过程。

小结：我们先找到1小壶水等于3杯水这对相等的量，就可以用3杯水代换1小壶水。看，解决生活中的问题是不是很有趣呢？

在练习设计时笔者就采用了这道生活问题，解决例题时，孩子们已能优化出相等的量互相替换，用推理优化来解决问题。先理解一大壶水可以倒2小壶水，一小壶水能够倒3杯水，这里面有相等的量就可以代换，用三杯水可以换一小壶，那么两小壶就可以用两个3杯水，就是6杯水来代换，一大壶水就可以倒6杯水。这道实实在在的生活题让学生们领悟到了用数学知识解决问题的愉悦，相信他们他们也会逐步养成带着发现问题，解决问题的眼光观察生活。

推理能力的养成不是一朝一夕的，而是一个不断渗透、循序渐进、由浅入深的过程。在这个过程中，教师需要不断地用数学思想“启迪”学生的思维，让学生在一次次的探索过程中，不断地反思、积累、感悟，直到最后变成自己的能力。

（作者单位：山东省青岛市李沧区实验小学）