铁路斜拉桥上无缝线路纵向附加力三维有限元分析

苏 尚 旭

(北京城建设计发展集团股份有限公司武汉分院，湖北 武汉　430000)



铁路斜拉桥上无缝线路纵向附加力三维有限元分析

苏 尚 旭

(北京城建设计发展集团股份有限公司武汉分院，湖北 武汉430000)

以某一铁路斜拉桥为例，建立了斜索、桥塔、轨道、桥梁、墩台、基础为一体的三维有限元模型，并采用该模型分析了斜拉桥铺设无缝线路后钢轨纵向附加力分布规律，对无缝线路在斜拉桥上的铺设研究有重要的意义。

斜拉桥，无缝线路，纵向附加力，有限元模型

桥上无缝线路与路基上的不同，其钢轨除了承受温度力作用以外，还承受桥上纵向附加力作用，包括伸缩力、挠曲力与断轨力等。计算这些附加力是检算轨道结构与桥梁墩台强度、稳定性的前提[1]。另外，不同于其他形式的桥梁，斜拉桥上无缝线路有着和其本身结构密切相关的一些特点：1)斜拉桥上无缝线路设计中进行梁轨相互作用分析时，需要考虑斜拉桥结构体系的特点。斜拉桥上部结构由梁、索、塔三类构件组成。斜拉桥是自锚体系，拉索承受巨大拉力，拉索的水平分力使主梁受压，塔、梁均为压弯构件。2)斜拉桥是柔性结构，斜索的垂度问题在斜拉桥的非线性分析中是必须要考虑的。由于斜索有一定的垂度，故其弹性模量有所损失。在实际计算中可以用等效弹性模量来模拟斜索，这样可以直接将非线性问题转化为线性问题考虑。

国内铁路斜拉桥上无缝线路纵向附加力计算目前较多借助通用有限元软件进行分析，计算模型亦多采用平面有限元模型。将多股钢轨叠合为一股，但依据《新建铁路桥上无缝线路设计暂行规定》规定，低温时钢轨假定只折断一股，平面有限元模型就难以模拟这一工况，因此有必要将钢轨分开模拟，更加贴合实际工程。

在相关文献[2]的基础上，本文采用有限元软件，结合实际工程，建立考虑两股钢轨的空间模型，并对该模型下的桥梁附加力进行计算，通过与平面模型的对比，分析斜拉桥附加力受力特点，给从事相关研究工作的人员提供一定的参考。

1　斜拉桥上无缝线路纵向附加力计算模型

本模型中，对斜拉桥进行简化处理，在遵循梁轨相互作用原理的条件下，将桥梁、斜索、桥塔、轨道、支座、墩台、基础视为整体结构。

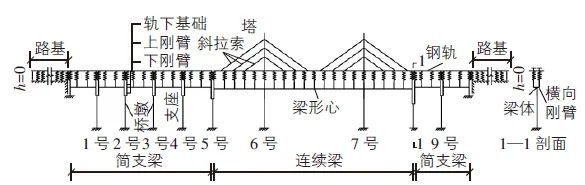
图1　某铁路斜拉桥上无缝线路纵向附加力计算三维有限元模型

两股钢轨在其实际空间位置分别用梁单位按实际轨枕间距离散；桥梁结构在截面中性轴位置，按照轨枕间距进行离散；用梁单位模拟桥塔；用杆单元模拟斜索；支座处伸出一竖向刚臂用于模拟桥梁下翼缘；在桥梁单元各节点处各伸出一横向刚臂，在刚臂末端向上各伸出一竖向刚臂用于模拟上翼缘；线路纵向阻力采用弹簧单位模拟；对于桥梁固定支座考虑固接，不考虑其变形；对于板式、盆式橡胶支座根据其力学性能用弹簧单元模拟；桥墩用梁单元进行离散，桥头路基各需考虑一段充分长的锁定长度。将钢轨模型、轨下基础模型、桥梁模型、拉索模型、桥塔模型、支座模型与墩台模型组装起来，就可以得到斜拉桥上无缝线路纵向附加力计算模型。图1为铁路斜拉桥上无缝线路纵向附加力计算三维有限元模型。

2　斜拉桥上无缝线路纵向附加力计算分析

以某铁路斜拉桥为例，主桥为预应力混凝土斜拉桥，跨度为48 m+96 m+48 m，结构形式为塔梁固结，塔墩分离，在6号墩设有固定支座。左边引桥为2×24 m+3×32 m预应力混凝土简支梁，支座布置为左固右活；右边引桥为32 m+24 m预应力混凝土简支梁，支座布置为左活右固。为适应铁路提速要求，将原普通线路铺设为温度应力式无缝线路。

2.1伸缩力

本文模型伸缩力计算结果见图2，伸缩力工况下的梁轨位移见图3。

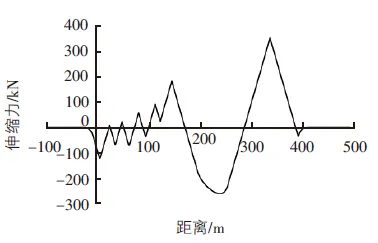
图2　单股钢轨伸缩力(梁体降温15 ℃)

图3　计算伸缩力时梁轨位移(梁体降温15 ℃)

根据计算结果显示，伸缩力计算结果为352 kN,与平面模型(352 kN)相比，相对误差为0.3%，可见，相同工况条件下，空间位置对其伸缩力几乎无影响，与伸缩力计算原理相符。

2.2挠曲力

挠曲力计算工况较多，选择有代表性工况作说明。采取主桥连续梁全桥加载。挠曲力结果见图4，挠曲力工况下梁轨位移图见图5。

根据计算结果显示，挠曲力计算结果为143.1 kN,与平面模型(139.8 kN)相比，相对误差为2.3%。可见，相同工况下，平面与空间模型对挠曲力影响较小，与挠曲力计算原理相符。

图4　单股钢轨挠曲力(全桥加载)

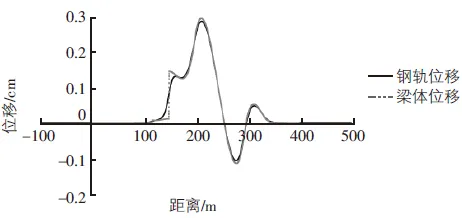
图5　计算挠曲力时梁轨位移(全桥加载)

2.3断轨力

为更贴合实际工程，考虑单股钢轨发生断轨的情况，本文模型断轨力计算结果见图6，伸缩力工况下的梁轨位移见图7。

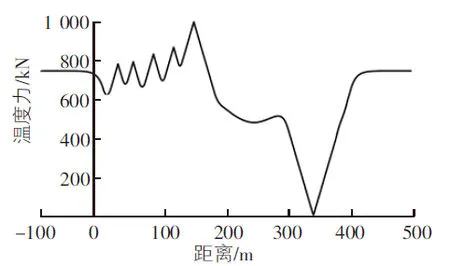
图6　钢轨断轨力(本文模型)

根据计算结果显示，空间模型下断轨时钢轨最大轴力计算结果为1 002 kN,与平面模型(983 kN)相比，相对误差为2%,两者相差不大。但空间模型断缝为4.4 cm，平面有限元模型结果为5.0 cm，相差12%，误差较大。本文模型在断轨工况中，仅考虑单股钢轨发生断轨情况，另外一根钢轨保持工作状态，并受联接制约，因此断轨工况下，空间模型轨缝较小，但两者相比，并未超限。

3　结语

本文采用有限元软件，用梁单元、杆单元、弹簧单元、质量单元模拟斜索、桥塔、轨枕、桥梁、支座、墩台、基础，结合实际斜拉桥梁工程，建立纵向附加力计算三维有限元模型，通过与平面模型对比得出以下结论：

1)由于红水河桥的自身跨度比较小，且斜缆垂度的非线性影响不超过1%，在建立模型时忽略考虑。斜拉桥作为加强型连续梁桥，其纵向力分布仍满足一般连续梁桥上纵向附加力规律。

2)两种模型对计算伸缩力与挠曲力不存在较大差异。

3)计算断轨力时，钢轨轴力变化较小，但轨缝相差12%，主要原因是两者在发生断轨时，考虑因素不同，平面模型受空间限制，考虑两股钢轨同时断轨，而三维模型中，仅考虑单股断轨，另一股钢轨处于工作状态，该工况更贴合实际工程，故空间模型下计算断缝要小。故由此可知，平面模型计算偏于安全。

4) 斜拉桥钢轨中的伸缩力很大，对轨道强度和稳定性会产生较大威胁，在无缝线路设计中，应把伸缩力计算作为一个控制因素。

[1]广钟岩，高慧安.铁路无缝线路[M].第4版.北京:中国铁道出版社，2005.

[2]徐庆元.高速铁路桥上无缝线路纵向附加力三维有限元静力与动力分析研究[D].长沙:中南大学，2005.

[3]铁建函[2003]205，新建铁路桥上无缝线路设计暂行规定[S].

[4]江万红,唐进锋,张建,等.刚构桥上无缝线路纵向附加力三维有限元分析[J].四川建筑，2008(6)：146.

[5]阴存欣.铁路桥梁纵向附加力的静动力非线性分析与仿真研究[J].中国铁道科学，2001(5)：95-97.

[6]徐庆元，陈秀方.连续梁桥上无缝线路附加力研究[J].中国铁道科学，2003,24(3)：19-20.

3D finite element analysis of additional longitudinal force of jointless track on the railway cable-stayed bridge

Su Shangxu

(WuhanBranchInstitute,BeijingCityConstructionDesignandDevelopmentGroupCo.,Ltd,Wuhan430000,China)

Taking the railway cable-stayed bridge as an example, the paper establishes 3D finite element model by integrating with the cable, bridge tower, rail, bridge, pier and foundation, and analyzes additional longitudinal force distribution law of the steel rail track after paving jointless track on the cable-stayed bridge, which has significant meaning for studying the jointless track paving on the cable-stayed bridge.

cable-stayed bridge, jointless track, additional longitudinal force, finite element model.

1009-6825(2016)21-0177-02

2016-05-13

苏尚旭(1988- )，男，硕士，助理工程师

U448.27

A