对线性调频雷达的正弦全波整流加权调频干扰*

谭　铭，王春阳，李　欣，宫　健，原　慧（空军工程大学防空反导学院，陕西西安710051）

对线性调频雷达的正弦全波整流加权调频干扰*

谭铭，王春阳，李欣，宫健，原慧
（空军工程大学防空反导学院，陕西西安710051）

提出了一种新的应答式干扰技术——正弦全波整流加权调频干扰。阐述了该干扰信号的产生机理，对其信号特点和移频的效果进行了分析。理论分析表明：根据相应参数的灵活选择，这种干扰能对线性调频雷达产生不同程度的假目标欺骗干扰和压制干扰效果，且需要较小的干扰功率。仿真实验证明了理论分析的正确性和实际应用的可行性。

电子对抗；加权调频干扰；线性调频信号

0　引言

现代雷达广泛应用线性调频信号以提高探测距离和距离分辨率。线性调频信号使探测距离和探测精度的矛盾得以解决，而且其脉冲压缩处理使目标回波产生高的处理增益，传统的噪声干扰无法获得其匹配增益，因此若需进行有效干扰，则要求干扰机必须输出高的干扰功率［1～3］。寻求一种功率利用效率高的信号，是电子对抗领域亟待解决的课题。

现阶段对线性调频雷达的干扰已经有很多研究，干扰样式多种多样，主要分为压制性干扰和欺骗性干扰两大类。在不同的场合进行合理的选择，两者均能达到较好的干扰效果，影响雷达的正常工作［4～6］。

本文根据线性调频脉冲压缩雷达信号处理的特点，提出一种新的干扰技术——正弦全波整流加权调频干扰，即通过干扰机对接收到的雷达信号附加全波整流正弦波频率调制，经过适当移频处理，得到干扰信号进行放大，再通过天线转发出去。这种干扰是在直接正弦波加权调频干扰基础上的改进型，能利用雷达脉冲压缩的处理增益，降低了干扰功率的要求，且相对直接正弦波加权调频干扰优势更明显。

1　干扰信号的产生机理

接收到的雷达信号可以表示为

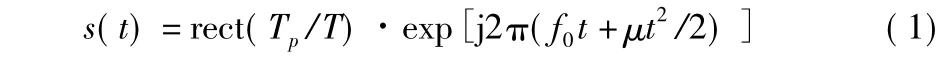
式中f0为载频，μ=B/Tp为调频斜率，B为带宽，Tp为时宽，T为周期，其瞬时频率为

全波整流正弦波调频信号p（t）的表达式为（以一个周期为例）

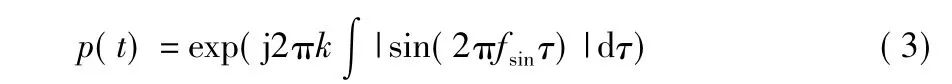
进一步得到

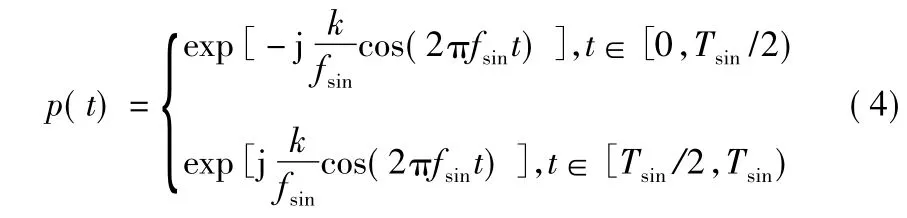
式中fsin全波整流正弦波调频信号频率，Tsin=1/fsin为信号周期，k为调幅系数，kf=k/fsin为调频系数。

干扰信号为

所以，干扰信号的瞬时频率为

这里，n（t）即为全波整流正弦波，满足式子 n（t）= |sin2πfsint|，图1是调频信号p（t）的时频关系图。

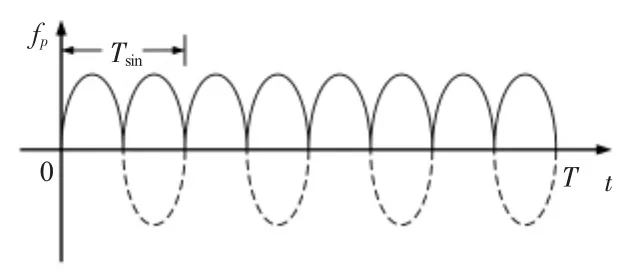
图1　调频信号时频关系图Fig 1　Time-frequency relationship diagram of frequency modulation signal

图2为干扰信号的时频关系。

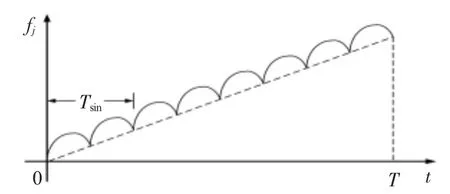
图2　干扰信号时频关系图Fig 2　Time-frequency relationship diagram of jamming signal

图2中虚线的斜率即为线性调频信号的调频斜率。

如果进行移频处理，则得到图3。

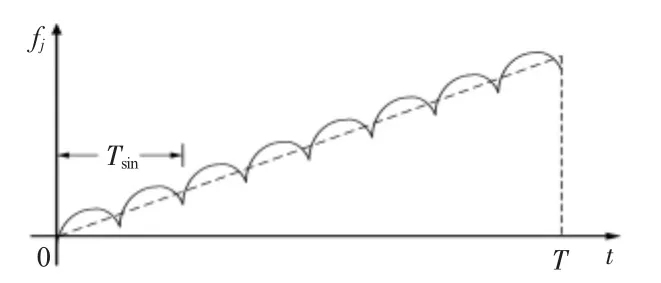
图3　移频后的干扰信号时频关系图Fig 3　Time-frequency relationship diagram of jamming signal after frequency shift

2　干扰频域特性与移频的影响

设s（t），p（t）和js（t）的频谱分别为S（f），P（f）和Js（f），可得干扰信号的频谱为

式中*为卷积运算，将调频信号p（t）进行傅里叶展开，

式中Ω=2πfsin为调频角频率，且系数Fn满足

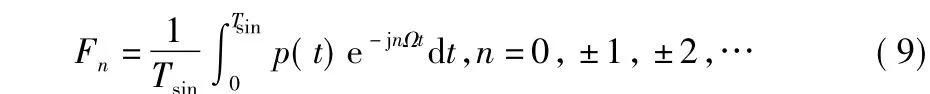
经化简可以得到

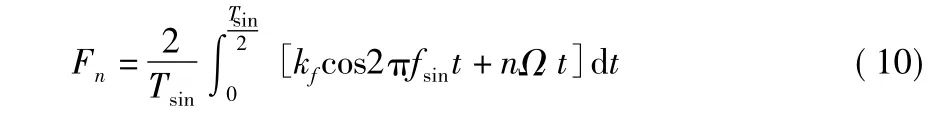
所以，可见调频信号p（t）的频谱为在频率0，Ω，2 Ω，…等离散频率上的离散谱，幅度取决于。

于是可以得到，干扰信号的形成即对接收到的雷达信号进行移频、加权、累加的结果。由于线性调频信号的模糊函数具有距离—多普勒耦合效应［7，8］，即多普勒频移和时延存在以下关系

所以，相对于中心频率来说，移频量的增大，会使得脉冲压缩后的幅度线性减小，并出现相应的展宽。通过图2可以看到，正弦全波整流加权调频干扰对雷达信号进行单侧的频移，并没有很好的利用好干扰效率，如果在这个基础上对其进行反方向的适度的移频，将会使干扰调频后的频率更接近雷达信号的频率，如图3所示，这样能量的利用更加充分。

3　干扰关键参数分析

3.1干扰影响因素

当调频信号的周期过小时，频率变化可以近似的认为是固定移频，移频量与kf有关；当周期过大时，并不能产生很好的移频效果，干扰信号与雷达信号近似，不能起到有效干扰的作用。因此，在选取调频信号周期的时候，应在信号时宽附近2个数量级内干扰才是相对有效的。

当调频系数kf取得过小时，对雷达信号的调制不明显，达不到干扰需要达到的效果；当其取得过大时，与雷达信号相差太大，干扰的峰值降低严重，不能很好地利用干扰效率。

进行正弦全波整流加权调频后移频的选择跟调频系数kf、调频信号频率fsin（即调频信号周期Tsin）有关，要想使干扰能量的利用效率最高，应使移频后总的移频量为0，因此可以得到式子

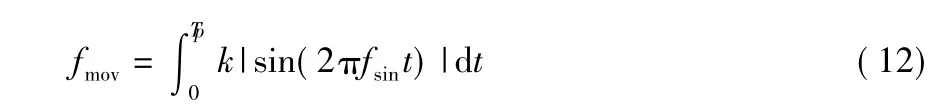
式中fmov为移频量。

3.2干扰效能分析

已知雷达信号时宽为Tp，信号时宽经脉冲压缩后变成1/B（B为信号带宽），由于压缩是无源的，根据能量守恒定理，可得

所以，该干扰功率增益为

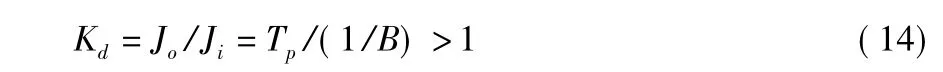
干信比增益为

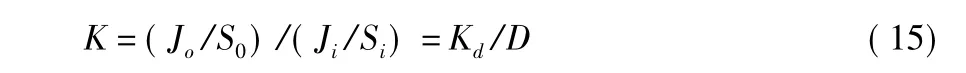
式中Kd为系统干扰功率增益，K为系统干信比增益，Ji，Jo和Si，S0分别为脉冲压缩前后的干扰功率和信号功率，为雷达信号经过匹配滤波器的脉压增益。

可见，该干扰功率增益大于1，干信比增益为Kd/D；射频噪声干扰功率增益小于1，干信比增益为1/D。灵巧噪声干扰信号具有较高的干扰功率利用率，与回波信号相关性强，干扰效果好。

4　仿真分析

仿真验证选取雷达参数：载频 f0=300 MHz，时宽Tp=50 μs，带宽B=5 MHz，周期T=200 μs。首先仿真得到目标回波经过脉冲压缩后的波形图与传统射频噪声干扰的效果图，如图4和图5。

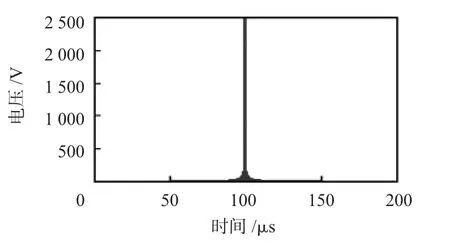
图4　目标回波脉冲压缩波形Fig 4　Pulse compression waveform of target echo

图5　传统射频噪声干扰Fig 5　Traditional RF noise jamming

可以看出，射频噪声干扰无法获得匹配滤波增益，干扰功率利用效率不高，不能进行有效干扰。

然后观察干扰信号移频前后的效果，令kf=5，Tsin= 10 μs得到图6（a）和图6（b）或者kf=30，Tsin=50 μs得到图6（c）和图6（d）。可以看出，移频前，干扰基本分布在目标回波的一侧，因移频，在目标回波的两侧均有大量干扰，且移频后干扰的频率更接近目标信号，产生的干扰能量利用效率也更高，能更加有效地实施干扰。

分析正弦全波整流加权调频干扰和直接正弦波加权调频干扰如图7。

其中，参数1～参数4分别为kf=5，Tsin=10 μs，kf= 15，Tsin=10 μs，kf=15，Tsin=20 μs，kf=30，Tsin=50 μs。

可以看出，正弦全波整流加权调频干扰移频后的效果相对直接正弦波加权调频干扰来讲，有以下优点：1）干扰的峰值更高，能量利用效率好；2）干扰没有在目标回波两

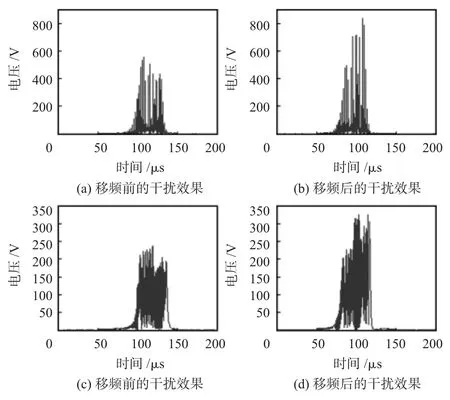
图6　移频前后的干扰效果对比Fig 6　Jamming effect comparison of before and after frequency shift

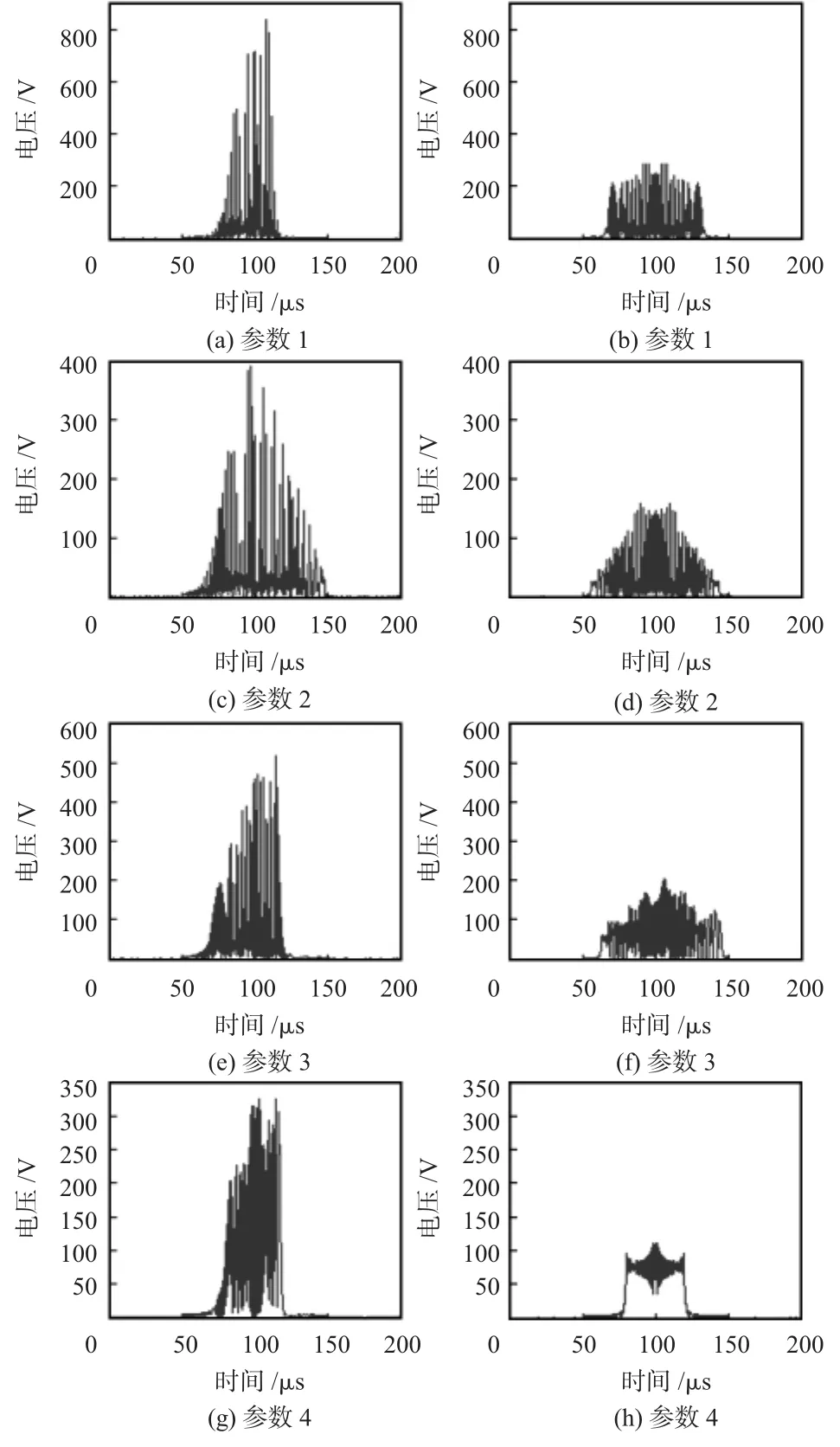
图7　两种干扰效果对比Fig 7　Two jammings effect comparison

侧对称分布，随机性更强；3）干扰的幅度起伏更大，欺骗干扰效果更好；4）进行压制干扰时，能量的利用更加充分，压制效果更好。缺点就是前者的干扰数量相对后者来说要少一些。

5　结束语

线性调频雷达是一种高分辨雷达，采用相参处理和匹配滤波技术，使得传统的压制噪声干扰的干扰效果大大降低。正弦全波整流加权调频干扰作为一种有效而灵活的干扰样式，既能产生假目标欺骗干扰效果，又能产生压制干扰效果，它是对接收到的雷达信号进行正弦全波整流加权调频，再经移频，然后通过放大转发形成的。这种干扰能利用脉冲压缩的处理增益，从而降低了干扰功率要求，通过改变相应的参数，可以灵活的产生不同效果的假目标欺骗干扰和压制性干扰，可根据实际需求进行合理选择。这种干扰在是直接正弦加权调频干扰的基础上进行的改进，干扰效果更好。

［1］丁鹭飞，耿富录，陈建春.雷达原理［M］.4版.北京：电子工业出版社，2010：488-512.

［2］丁鹭飞，张平.雷达系统［M］.西安：西安电子科技大学出版社，1984：7-18.

［3］赵国庆.雷达对抗原理［M］.西安：西安电子科技大学出版社，1999.

［4］张煜，杨绍全，崔艳鹏.对线性调频雷达的正弦加权调频干扰技术［J］.系统工程与电子技术，2007，29（4）：544-547.

［5］郭俊杰，王兴华，王星，等.雷达信号频率调制的灵巧噪声干扰技术［J］.西安电子科技大学学报：自然科学版，2013，40（4）：155-160.

［6］张养瑞，高梅国，李云杰.LFM脉冲雷达恒虚警检测的协同压制干扰［J］.系统工程与电子技术，2014，36（11）：2156-2163.

［7］Fitzgerald R J.Effect of range-Doppler coupling on chirp radar tracking accuracy［J］.IEEE Trans on AES，1974，10（4）：528-532.

［8］Yang Shaoquan，Zhang Zhengming.ECM for chirp radar［J］. Journal of Xidian University，1991，18（3）：24-30.

王春阳，通讯作者，E—mail：Wcy_kgd_cn@163.com。

Sinusoidal full wave rectification weighted frequency modulation jamming technique for countering LFM radar*

TAN Ming，WANG Chun-yang，LI Xin，GONG Jian，YUAN Hui
（Air and Missile Defense College，Air Force Engineering University，Xi'an 710051，China）

A new technique of transponder jamming is proposed which is named sinusoidal full wave rectification weighted frequency modulation jamming.Generation principle of jamming signal is being presented，its features and effect of frequency shift is analyzed.Theoretical analysis shows that this jamming can produce different degrees of false targets deceptive jamming and cover jamming effects，according to flexible choice of corresponding parameters and require lower jamming powers.The simulation results justify the correctness of theoretical analysis and the feasibility of practical application.

electronic countermeasures；weighted frequency modulation jamming；linear frequency modulation （LFM）signal

TN974

A

1000—9787（2016）06—0031—03

10.13873/J.1000—9787（2016）06—0031—03

2015—10—19

国家自然科学基金青年科学基金资助项目（61501500）；航空科学基金资助项目（20130196001）

谭铭（1992-），男，四川南充人，硕士研究生，主要研究方向为雷达与电子战新技术。