基于单纯形法的蝙蝠算法

肖辉辉

(1.河池学院　计算机与信息工程学院， 广西　宜州　546300; 2.江西财经大学　信息管理学院， 江西　南昌　330013)



基于单纯形法的蝙蝠算法

肖辉辉1,2

(1.河池学院计算机与信息工程学院， 广西宜州546300; 2.江西财经大学信息管理学院， 江西南昌330013)

针对蝙蝠算法局部搜索能力低、迭代后期收敛速度较慢的缺陷，提出基于单纯形法的蝙蝠算法。该算法对进入下一次迭代前对部分较差个体采用单纯形法的扩张、收缩/压缩操作，提高局部搜索能力，进而提高算法的寻优能力。对6个CEC2005 benchmark测试函数进行测试比较，仿真结果表明，改进算法的收敛速度、收敛精度、鲁棒性等寻优性能明显优于基本的蝙蝠算法和参考文献对比算法。

蝙蝠算法；寻优性能；单纯形法；适应度值

2010年，Xinshe Yang提出一种新型的元启发式群智能算法—蝙蝠算法(Bat Algorithm, BA)[1]，该算法主要针对蝙蝠在寻找食物时利用声呐回声来确定食物的位置及其对障碍物的避躲进行模拟，具有分布性、实现简单及并行性等优点。蝙蝠算法已经在工程科学和自然科学领域中得到广泛的应用，如多目标优化[2]、PFSP调度问题[3]、大规模优化问题[4]等。但是，蝙蝠算法与粒子群等群智能算法一样，也存在局部搜索能力低，迭代后期收敛速度慢等不足，尤其对于多局部极值、高维的较复杂优化问题。为此，国内外不少学者对算法进行了改进：谢健等人提出了一种基于Lévy飞行轨迹的蝙蝠算法(LBA)[5]，该算法在蝙蝠位置的更新公式中引入具有随机性的Lévy飞行机制，提升算法的性能；赖锦辉提出了基于部落结构的多种学习机制蝙蝠优化算法(GDBA)[6]，该算法将蝙蝠群体划分成部落，在各部落间建立相互学习机制，提高了算法的局部搜索能力。上述这些改进在一定程度上避免了局部极值，提高了算法的寻优能力，仍未使算法完全避免陷入局部极值，其收敛精度、稳定性、收敛速度等方面仍有待改进。

针对蝙蝠算法的局限性，本文提出了一种基于单纯形法的蝙蝠算法(SMBA算法)，该算法在进入下一次迭代前，对部分蝙蝠较差个体进行单纯形法操作，利用其扩张、收缩/压缩操作产生的较优蝙蝠取代最差蝙蝠，提高局部搜索能力。通过6个CEC2005 benchmark测试函数的仿真实验结果，验证了改进算法的有效性和优越性，SMBA算法较BA算法在较大程度上有效地避免了过早收敛，增强了算法的局部搜索能力，提高了算法的收敛速度、稳定性及收敛精度等性能。

1　BA算法

蝙蝠算法是模拟蝙蝠利用本身特有的声呐功能进行探测、定位物体的行为的搜索方法。该算法中将蝙蝠个体与求解问题搜索的可行解进行对应，把蝙蝠个体搜索猎物和向猎物移动的过程对比为算法的搜索和优化迭代过程，蝙蝠个体位置的好与差由函数的适应度值来决定，即算法的优化迭代过程即为蝙蝠个体由差的位置向好的位置靠近的过程。

BA算法的基本步骤如下：

Step1初始化参数：种群数n，最大脉冲音量A，最大脉冲率r，音量的衰减系数α，搜索频率的增强系数γ，搜索精度ε或最大迭代次数N。

Step2随机初始化蝙蝠的位置xi，并求解当前最优解x*。

Step3按如下公式更新蝙蝠的搜索脉冲频率、速度和位置：

fi=fmin+(fmax-fmin)×β， (1)

Step4得到随机数R，若R>ri，则求出当前最优个体并对其进行随机扰动得到一个新的局部个体解。

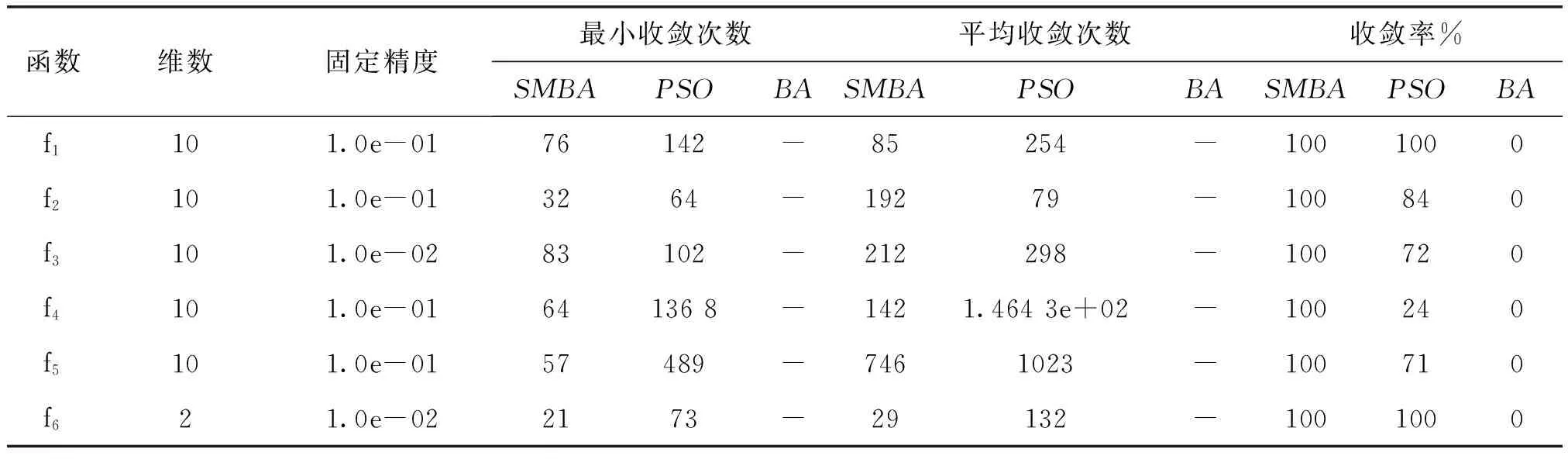
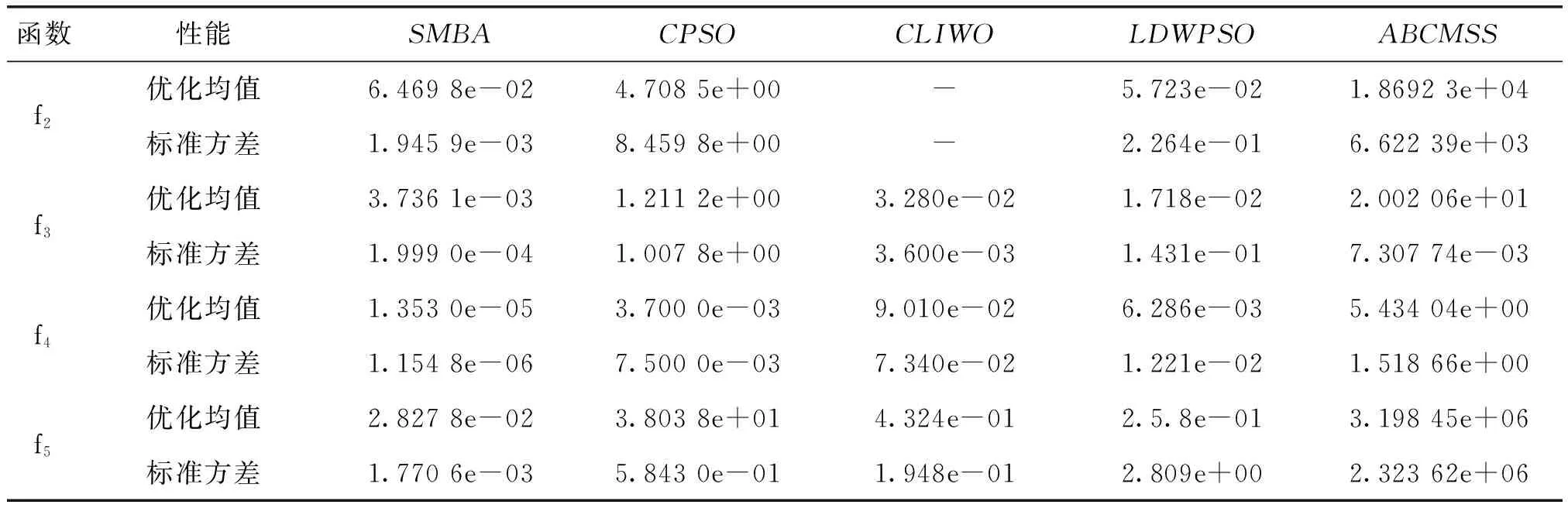
Step5产生随机数rand，若rand

Step6计算蝙蝠种群的适应度值，保存当前的最优值及其最优解。

Step7判断迭代执行条件，若不满足则程序结束，并保存全局最优值及对应的最优解，否则，转Step3。

Step8输出全局最优值和最优解。

2　SMBA算法

2.1单纯形法

单纯形法是一种局部搜索能力较强的搜索方法[7]，具有计算简单、搜索速度快的优点。单纯形法的基本思想为：在一个d维的空间构造一个d+1个顶点的多面体，求出该多面体的d+1个顶点的适应度值，对比适应度值求解出最优个体、次优个体及最差个体，然后对最差个体进行反射、扩张、压缩/收缩操作使其转为较好个体，形成新的多面体。因此，单纯形法是通过比较单纯多面体顶点的适应度值，来对单纯多面体最差个体进行改进，逐步向最优值靠近的搜索方法。该方法中的反射操作能使最差个体随机地向重心的反方向搜索，搜索解空间中的所有可行解；扩张操作能使新生成的最优值个体继续向距最差个体更远的反方向搜索。这样，若当前最优值个体是局部极小点，则扩张操作能使该个体跳出局部极小值区；收缩操作能使生成的较差的反射点收缩调整到更好位置。

单纯形法的步骤如下：

Step1初始化：计算所有点的适应度值，找出最优点ng，次优点np，其对应的适应度值分别为f(ng)和f(np)，中心位置nc=(ng+np)/2。

Step2生成反射点nx：找出m个较差的点r，其适应度值为f(r)，并对r点进行反射：nx=nc+∂(nc-r)，∂为反射系数。

Step3扩张操作：若f(nx)

Step4压缩操作：若f(nx)

Step5收缩操作：若f(nr)>f(nx)>f(np)，则进行收缩操作，nw=nc-δ(r-nc)，nw为得到的压缩点，δ为收缩系数，其取值与压缩系数β一致，若分f(nw)

本文提出在BA算法中引入单纯形法，在蝙蝠种群进入下一次迭代前，对多个较差的蝙蝠个体利用单纯形法搜索策略进行优化，增强了BA算法的局部搜索能力。

2.2SMBA算法的实现步骤

针对BA算法易陷入局部极值、局部搜索能力低、进化后期收敛慢等不足，本文采用单纯形法策略，提出了SMBA算法，改进算法中利用2.1小节的单纯形法策略作用于BA算法，使蝙蝠种群中较差的部分个体在进入下一次迭代前进行反射、扩张、压缩/收缩操作使其转为较好蝙蝠个体，在很大程度上提高了算法的寻优性能。

SMBA算法的具体实施步骤如下：

Step1 初始化SMBA算法的参数:种群数n，转换概率p，最大脉冲音量A，最大脉冲率R，音量的衰减系数α，搜索频率的增强系数γ，搜索精度ε或最大迭代次数N，最差个体数m，反射系数∂，扩张系数φ，压缩系数β，收缩系数δ。

Step2执行BA算法的Step2～Step5。

Step3计算所有解的适应度值，找出最优点Xg，次优点Xp，及其对应的适应度值(Xg)和f(Xp)，中心位置Xc。

Step4对较差蝙蝠Xr进行反射，得到反射点Xx。

Step5若f(Xx)

Step6若f(Xx)

Step7若f(Xr)>f(Xx)>f(Xp)，执行收缩操作得到收缩点Xw，若f(Xw)

Step8重复执行 次Step6～Step9来更新m个较差蝙蝠的位置。

Step9计算蝙蝠种群的适应度值，并更新全局最优值和全局最优解。

Step10判断迭代执行条件，若不满足则退出程序，并保存当前最优值及对应的最优解，否则，转Step2。

3　实验仿真与分析

为了验证本文算法的正确性和有效性，通过对6个包括单峰、多峰、低维、高维的测试函数进行仿真来验证算法的改进效果，测试函数选用CEC2005 benchmark测试函数中的一部分，测试函数如下：

该函数是一个单峰函数，函数在x*=(0,0,…,0)处取得全局min(f1(x))=0。

该函数是一个多峰函数，函数在x*=(0,0,…,0)处取得全局min(f2(x))=0。

(3)Ackley函数：

该函数是一个多峰函数，在x*=(0,0,…,0)处取得全局最小值min(f3(x))=0。

该函数是一个多峰函数，在x*=(0,0,…,0)处取得全局最小值min(f4(x))=0。

该函数是一个单峰函数，在x*=(0,0,…,0)处取得全局最小值min(f5(x))=0。

该函数的是一个二维多峰函数，在x*=(0,0)处取得全局最小值min(f6(x))=-1。

本文实验的参数设置为：种群个数n=20，维数d=10(函数f6的维数d=2)，最大迭代次数N=200。另外，SMBA算法中，较差蝙蝠数m=6，反射系数∂=0.9，扩张系数φ=1.2，压缩系数β=1.5，收缩系数δ=1.5。

为了验证本文改进算法的寻优性能、可行性及正确性，仿真实验方法为：(1)固定算法的迭代次数，测试2种算法的寻优性能；(2)给定函数的收敛精度，测试SMBA、PSO和BA算法的稳定性和收敛性；(3)与参考文献算法对比，测试本文算法的鲁棒性和寻优精度，并进一步验证SMBA算法的寻优精度。

3.1固定迭代次数的性能分析

本小节设置固定迭代次数N=200，为了避免算法的偶然性带来的性能比较上的误差，比较算法均对每个测试函数独立运行25次，计算其最优值、优化均值、最差值和标准方差，实验结果见表1，其中，寻优成功率=(找到最优解的次数)/总运行次数。在实验中，假定：|实际求解的最优值-理论最优值|<0.001，则认为算法成功地找到最优值。

从表1中可以看出，对于所有测试函数，本文提出的SMBA算法的寻优性能在很大程度上均优于基本BA算法。对于所有测试函数，BA算法的寻优成功率都为0，而SMBA算法，函数f1、f3、f4的寻优成功率都为100%，其它3个函数的寻优成功率也较高；对于函数f1～f5，SMBA算法的最优值、优化均值、最差值和标准方差均较BA算法有较大的提高，最多相差11个数量级；对于二维函数f6，SMBA算法能找到最优值，而BA算法不能。为了便于观察改进算法及基本蝙蝠算法的寻优收敛效果，图1是该两种算法求解6个测试函数收敛图，形象地展示了SMBA算法和BA算法的对比适应度值的迭代下降过程和全局最优解的收敛速度。从图1中可得出，对于6个测试函数，SMBA算法的收敛精度和收敛速度均较BA算法要好。这表明，本文提出SMBA算法具有更好的寻优能力，其收敛速度、优化精度明显优于BA算法。

表1　2种算法在固定迭代次数下的寻优性能比较

图1　2种算法在函数f1～f6上的收敛曲线

3.2固定收敛精度的性能分析

为了验证本文算法的收敛程度，在给定的固定精度下，对所有测试函数独立运行25次，SMBA算法、BA和PSO算法分别对比其最小收敛次数、平均收敛次数及收敛率，其中，收敛率=达到固定精度的迭代次数/总运行次数，其结果如表2所示，表中“-”表示寻优失败。本小节的3种算法的种群数为25，最大迭代次数为2 000，当前迭代次数超过最大代次数时，则认为寻优不成功。从表2可知，对于函数f1～f6， BA算法都无法收敛，SMBA算法的收敛率都为100%，远远高于对比算法，同时其最小收敛次数及平均收敛次数也明显低于对比算法。实验数据证明，本文改进算法在收敛性、鲁棒性性能上得到明显的提高。

表2　固定精度下的最小收敛次数、平均收敛次数和收敛率对比

3.3与参考文献算法性能比较

为了进一步验证本算法较好的稳定性和较高的寻优精度，证明本文改进算法的优势，限于篇幅，只选用函数f2～f5与参考文献中的CPSO[8]、CLIWO[9]、LDWPSO[10]、ABCMSS[11]算法对比，为了文中前后数据的一致性，本小节中的SMBA数据来自3.1小节，其结果如表3所示。其中，本文算法的迭代次数为200、种群数为20，除参考文献[9]的迭代次数为200、种群数为15外，其他参考文献的迭代次数和种群数均较大，分别为6 000(30)、2 000(300)和2 000(100)，括号中的为种群数。由表3可知，在测试参数较参考文献要严格的条件下，SMBA算法的优化性能(优化均值、标准方差)都能较参考文献中的其他群智能优化算法有较大的提高。对于函数f2～f5，SMBA的优化均值、标准方差都在较大程度上好于其他参考文献算法。其中，优化均值的性能最大相差8个数量级，标准方差的性能最大相差9个数量级。种群数和迭代次数这两个参数值是影响算法寻优性能的主要因素，且这两个参数值与算法的时间复杂度成正比例关系。仿真结果表明，本文SMBA算法的收敛精度和稳定性均得到较大的提高，进而说明SMBA算法是可行的和有效的。

表3　SMBA算法与参考文献算法的优化均值和标准方差比较

4　结束语

蝙蝠算法是一种新的群智能算法，但其亦存在早熟收敛、收敛精度较低、算法后期收敛速度慢等不足。为此，本文算法引入单纯形法策略，提高了局部搜索能力，进而提高算法的整体寻优性能。通过6个CEC2005 benchmark测试函数的测试，仿真结果表明，改进算法是可行和有效的，单纯算法使BA算法的整体性能得到一定程度地提高。

[1] Yang X S. A new metaheuristic bat-inspired algorithm[C]∥ Nature Inspired Cooperative Strategies for Optimization(NISCO 2010)，Studies in Computational intelligence 284.Berlin Eidelberg: Sprin-Verlag,2010:65-74.

[2] YANG X S. Bat algorithm for multi-objective optimisation [J].Int.J.Bio-Inspired Computation, 2011,3(5):267-274.

[3] 盛晓华,叶春明.蝙蝠算法在PFSP调度问题中的应用研究[J].工业工程,2013,16(1):119-124.

[4] 黄光球,赵魏娟,陆秋琴.求解大规模优化问题的可全局收敛蝙蝠算法[J].计算机应用研究, 2013,30(5):1323-1328.

[5] 谢健,周永权,陈欢.一种基于Lévy飞行轨迹的蝙蝠算法[J].模式识别与人工智能, 2013,26(9):829-837.

[6] 赖锦辉.基于部落结构的多种学习机制蝙蝠优化算法 [J].计算机应用研究,2015, 32(2):364-367.

[7] NELDER J A,MEAD R. A simplex method for function minimization[J].Computer journal, 1965,7(4):308-313.

[8] 赵新超,刘国莅,刘虎球,赵国帅. 基于非均匀变异和多阶段扰动的粒子群优化算法[J]. 计算机学报, 2014,37(9): 2058-2070.

[9] 刘挺,王联国. 基于云模型的入侵杂草优化算法[J].计算机工程,2014,40(12):156-160.

[10] 乔俊飞,傅嗣鹏,韩红桂.基于混合变异策略的改进差分进化算法及函数优化[J].控制工程,2013,20(5):943-947.

[11] 王志刚.一种改进搜索策略的人工蜂群算法[J].计算机仿真, 2014,31(10):291-295.

[Abstract]Bat algorithm based on simplex method was presented to overcome the poor capacity in local searching and low speed of convergence of bat algorithm. The algorithm uses the expansion and contraction/compression operation of simplex method to enter the next iteration of individuals to enhance the capacity of global optimization, and to improve the convergence speed. The six CEC2005 benchmark functions were tested and compared and the simulation results show that the proposed algorithm has the advantages of better global searching ability, faster convergence and more precise convergence than those of the basic bat algorithm and the reference comparison algorithm.

[Key words]bat algorithm; optimization ability; simplex method; fitness

[责任编辑刘景平]

Bat Algorithm Based on Simplex Method

XIAO Hui-hui1,2

(1. School of Computer and Information Engineering, Hechi University, Yizhou, Guangxi 546300, China;2. School of Information and Technology, Jiangxi University of Finance and Economics,Nanchang, Jiangxi 330013, China)

TP301.6

A

1672-9021(2016)02-0060-07

肖辉辉(1977-)，男，江西永新人，河池学院计算机与信息工程学院副教授、实验师，主要研究方向：智能计算、情感分析。

广西高校科研基金资助项目(KY2015LX332, KY2015LX334)；河池学院科研基金资助项目(XJ2015QN003)；河池学院“计算机网络与软件新技术”重点实验室资助项目(院科研〔2013〕3号)；江西省研究生创新基金资助项目(YC2015-B054)；河池学院教改基金资助项目(2014EB002)。

2015-11-20