基于涡格法的螺旋桨剖面拱线设计

饶志强，杨晨俊

1上海交通大学海洋工程国家重点实验室，上海2002402高新船舶与深海开发装备协同创新中心，上海200240

基于涡格法的螺旋桨剖面拱线设计

饶志强1，2，杨晨俊1，2

1上海交通大学海洋工程国家重点实验室，上海200240
2高新船舶与深海开发装备协同创新中心，上海200240

船舶螺旋桨的叶剖面形状与其负荷形式、效率、空泡等水动力性能密切相关。剖面拱线与剖面的负荷分布有直接关系。为了设计给定负荷分布的剖面拱线，提出用升力分布定义螺旋桨剖面拱线的负荷分布，在此基础上对升力分布进行参数化表达，并进行拱线设计。拱线的设计采用Newton-Raphson迭代方法使拱线的升力分布满足给定值，拱线的性能计算采用基于薄翼理论的二维涡格法。计算表明：涡格法与Newton-Raphson迭代方法相结合能够精确并快速设计满足给定升力分布的拱线。最后，修改升力分布的部分参数，并由此设计了SJ系列拱线供剖面设计参考。

螺旋桨叶剖面；拱线设计；升力分布；涡格法；SJ系列拱线

网络出版地址：http://www.cnki.net/kcms/detail/42.1755.TJ.20160729.0945.012.html期刊网址：www.ship-research.com

引用格式：饶志强，杨晨俊.基于涡格法的螺旋桨剖面拱线设计［J］.中国舰船研究，2016，11（4）：38-43.

RAO Zhiqiang，YANG Chenjun.Camber lines design approach of propeller blade sections based on the vortex lattice method［J］.Chinese Journal of Ship Research，2016，11（4）：38-43.

0　引　言

剖面形状对螺旋桨的水动力性能有直接影响。在剖面设计中，NACA系列的剖面［1］因其优良的抗空化性能而被设计者采用，比如NACA-66（mod）厚度分布和a=0.8拱线组合。但NACA剖面提出的时间很早，之后螺旋桨剖面（或称翼剖面）设计也已经发展了几种方法，这些方法主要有单点设计法、多点设计法、面元法和优化设计方法等［2］。单点法以Lighthill［3］方法为代表，做法是给定一个攻角和压力分布，通过保角变换设计剖面。多点法以Eppler［4］方法为代表，它是在剖面表面分段给出不同攻角的速度分布、设计剖面。由于分段处理，它为改善剖面在设计和非设计工况下的空泡性能提供了潜力。一些学者对Eppler方法在剖面设计中的应用进行了研究。Eppler等［5］和Shen等［6］将该方法推广到水翼设计中。王大政等［7-8］基于Eppler方法提出了可以控制最大厚度和拱度的剖面设计方法，并研究了剖面参数对空泡特性的影响。Zhou等［9］将Eppler方法设计的剖面直接应用到螺旋桨上。面元设计方法是对初始剖面进行扰动并做迭代计算，使其满足给定压力分布。处理方法主要有2种：一种是直接在剖面上布置控制点，并对其进行摄动和迭代计算，这些工作以苏玉民等［10］和蔡昊鹏等［11］的工作为代表；另一种是用B样条拟合并扰动拟合曲线控制点，谭廷寿等［12］和李俊华等［13］都采用该方法设计剖面，所不同的是前者拟合拱线而厚度不变，后者对表面进行拟合。前述设计方法的共同点都是需要按给定压力或者速度分布进行设计，但在设计初始阶段合理的压力和速度分布可能并不容易给定。给定值有缺陷可能对几何或计算压力分布的光顺性造成影响，文献［11］讨论了这个问题。另外，给定压力分布直接设计剖面可能会产生非常厚的剖面，文献［13］中提出该问题并通过减小空泡裕度解决剖面过厚的问题。面对设计中的问题，优化方法成为剖面设计的另一种选择。黄胜等［14］和常欣等［15］在剖面上下表面叠加基函数并采用多目标优化算法设计剖面。曾志波［16］和龙文等［17］基于Eppler方法对螺旋桨剖面进行了优化设计。在优化过程中，文献［14-15］和文献［16］分别对基函数的叠加量或者剖面最大厚度做了约束。

分析部分针对空泡性能的研究成果，特别是Eppler优化设计结果［16-17］，可以看出满足约束的最优设计剖面有如下特征：最大厚度位置向导边前移，增加叶背和叶面片空泡裕度，最大拱度位置向随边后移将负荷向随边移动［16］。本文作者曾针对固定厚度分布不变，采用面元法设计了具有不同拱线的剖面，并考察载荷分布对空泡性能的影响［18］。计算表明：载荷的移动对剖面空泡斗的上下位置有明显的影响。如此可以理解：载荷的移动在一定程度上能够改变空泡性能。这样问题的关键变成了如何设计具有给定载荷的拱线。如能实现给定载荷设计，拱线的几何设计问题实际上也就变成了载荷设计。

本文将针对上述问题对载荷分布用升力分布来定义，对其进行参数化表达，并采用Newton-Raphson迭代方法设计满足给定升力分布要求的拱线，拱线性能的计算采用二维涡格法。最后，修改给定升力分布的部分参数，设计SJ系列拱线供参考。

1　拱线设计方法

1.1升力分布的定义

升力分布（CLx）定义为升力在拱线弦向的密度，具体定义为微段弦长上的升力系数与微段弦长的比，如式（1）所示。

式中：ΔCL为对应的升力系数；Δc为微段弦长。由于拱线没有厚度，因此可用薄翼理论来求解。

在零厚度薄翼理论中，薄翼的升力系数（CL）为［19］

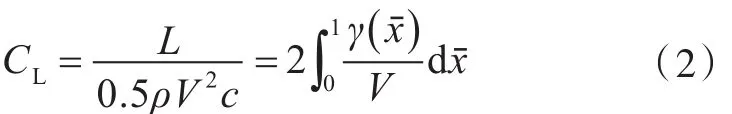
式中：L为剖面总升力；ρ为流体密度；V为来流速度；c为弦长；xˉ为无因次的弦向坐标；γ（）xˉ为弦向环量密度。

根据式（1）升力分布的定义，容易得到零厚度拱线的升力分布为

即在基于薄翼理论的拱线设计中，给定升力分布可以理解为2倍的给定环量密度在弦向的分布。采用二维涡格法可数值求解拱线的环量密度和升力分布。另外，通过升力分布的定义可知，剖面升力系数可由升力分布在弦向上的积分得到。

1.2升力分布的参数化表达

获得升力分布的定义后，需要给定升力分布的形式。这里采用5段线来给定升力分布的形式。如图1所示，升力分布由3条直线（L1～L3）和2条相切圆弧（C1和C2）构成，整条升力分布曲线各段光顺连接。

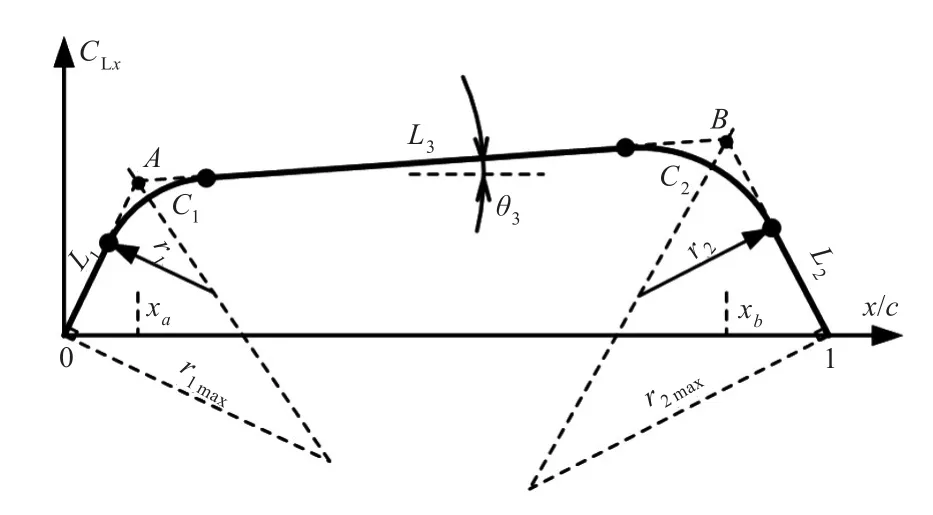
图1　升力分布的参数化表达Fig.1　Parametric representation of lift distribution

用5个参数可确定整个升力分布曲线，包括：

1）第1个角点A的位置xa；

2）第2个角点B的位置xb；

3）圆弧C1的相对半径，r1=Ar1r1 max；

4）圆弧C2的相对半径，r2=Ar2r2 max；

5）第3段直线L3的斜率角θ3。

式中：r1 max和r2 max分别为2段圆弧的最大半径，此时，L1和L2这2条直线长度为0。参数 Ar1和 Ar2为最大半径的比率，取值在0～1之间，用于控制C1和C2的半径。5个参数外加给定升力系数CL，即可通过迭代的方法获得整条升力分布曲线。在这种参数化定义中，拱线导边和随边的升力分布都为0，即载荷为0。第3段线的角度θ3可以控制升力分布的前移或者后移。如果调整A角和B角点位置，以及圆弧C1和C2的半径大小还可以对最大升力分布的位置进一步进行移动。这是一种直接对载荷分布进行控制的方法。尽管调整环量分布可以达到载荷调整的效果，但升力分布的定义更直观。

1.3拱线设计过程

拱线的设计以升力分布为目标。首先，选择一个初始拱线，在初始拱线上设置M+1个控制点，如图2所示。

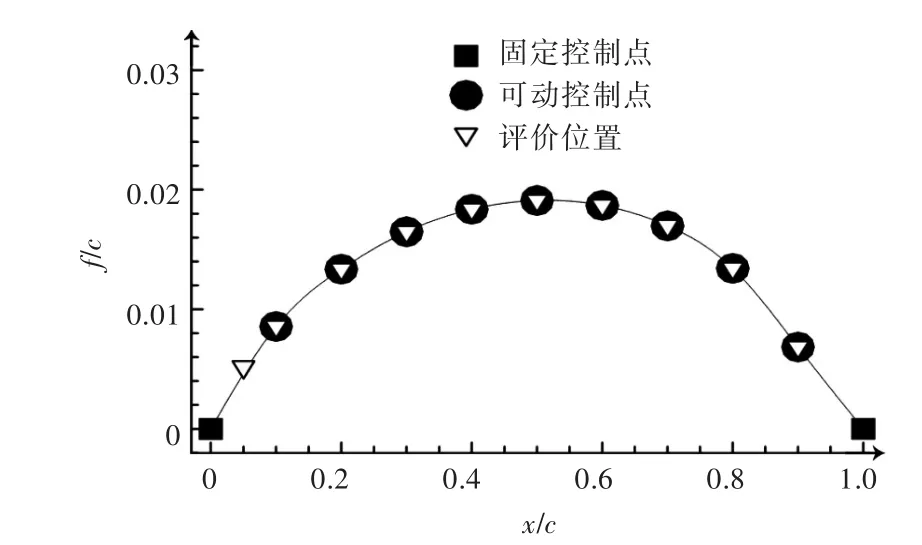
图2　拱线上控制点布置Fig.2　Control nodes arrangement on camber line

图中，x/c和f/c分别为无因次弦长位置和拱度弦长比，导边和随边为固定控制点，其他为可动控制点。对攻角和可动控制点进行摄动，以获得摄动量对弦向某些位置（称为评价位置）升力分布的影响。本文中评价位置与可动控制点的位置重合。由于增加了攻角的摄动，因此在导边和第一个可动控制点之间增加一个评估位置来构建M阶雅可比矩阵，如式（4）所示。

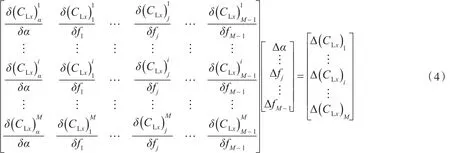
对新的拱线和攻角再进行摄动，直到评价位置上的升力分布计算值和给定值达到容差为止，本文容差为 1.0×10-4，这个设计过程即为Newton-Raphson迭代过程。在设计过程中，摄动初始拱线拱度为0，初始攻角为0.5°。

拱线的计算方法采用二维涡格法，即将拱线分成若干单元（本文取120个单元）。在每个单元的1/4长度处布置一个点涡，并将3/4位置作为单元控制点的位置，物面不可穿透边界条件在单元控制点上满足。涡格法的具体实施可见文献［19-21］的相关章节。

这里举一个例子详细说明迭代结果。在这个例子中，θ3=0°，xa=0.1，xb=0.85，Ar1=0.2，Ar2=0.2，设计升力系数为CL=1.0。总控制点个数为31个（对应雅可比矩阵阶数M=30），其弦向位置由升力分布的5段线决定。图3为设计过程中拱线随迭代次数的变化。可以看出，迭代3次后计算结果收敛。图4为给定升力分布、设计拱线的升力分布以及评价位置处升力分布的比较。可以看出，设计结果和给定的目标十分吻合。这说明本方法迭代计算量少，设计结果精确。

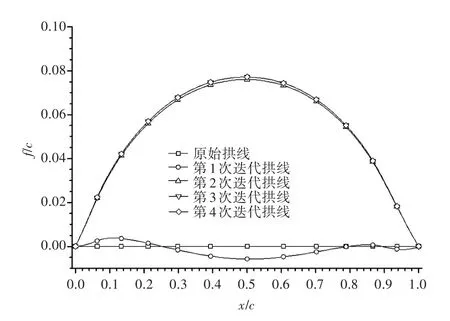
图3　设计过程中拱线的变化Fig.3　Camber lines during iterations

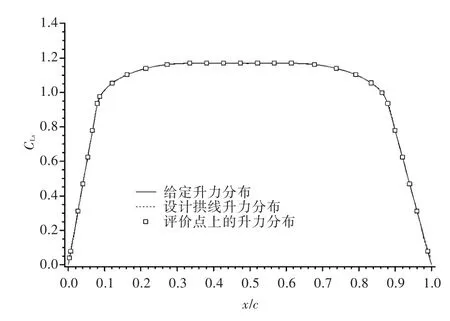
图4　给定和设计拱线的升力分布比较Fig.4　Comparison of given and designed lift distributions

在文献［18］中也讨论过剖面设计，但剖面的性能计算基于面元法。如果将剖面的厚度限定得很小，摄动剖面的拱线，也能通过Newton-Raphson方法设计出来。但由于厚度的影响不能完全忽略，实际计算时发现采用面元法的设计过程不太稳定，设计拱线也可能会出现不光顺的情况。这可能是由于文献［18］中升力分布的定义和计算是在剖面的上下表面对应位置插值造成的，而本文涡格法的计算中升力分布和环量密度直接相关，无需插值计算。由于涡格法能够获得稳定、光顺的拱线，是一种比较理想的方法，这里仅讨论涡格法的计算结果。

2　SJ系列拱线

针对不同的第3段直线斜率角θ3，给定不同的升力分布曲线，设计了系列拱线，其中，升力分布曲线的其他参数仍为：xa=0.1，xb=0.85，Ar1=0.2，Ar2=0.2，CL=1.0。这一系列的拱线命名为SJ系列拱线，其中SJ后第1位数字代表斜率角θ3的正负（0为负，1为正），后2个数字代表角度。如SJ015，代表θ3=-15°时的设计拱线。图5为部分SJ系列拱线的计算升力分布曲线。由于设计结果与给定升力分布十分吻合，故没有提供给定升力分布的结果。

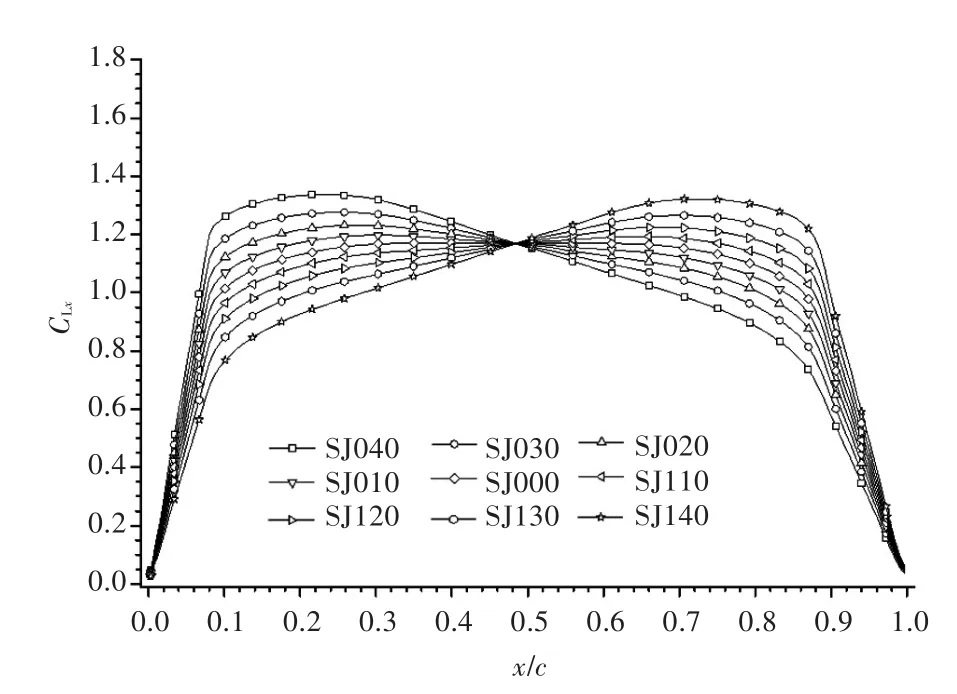
图5　SJ系列拱线的计算升力分布Fig.5　Calculated lift distributions of SJ series camber lines

图6为对应的部分SJ系列的无因次拱线图，其中f/fmax为弦向拱度与最大拱度比值。从图中可以看出，拱线的最大拱度位置随升力分布的前移或后移而分别前后移动。

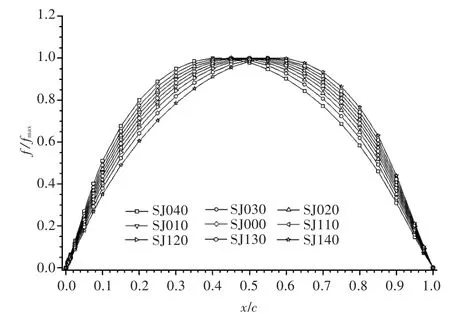
图6　SJ系列无因次拱线图Fig.6　Non-dimensional SJ series camber lines

表1为SJ系列拱线的攻角α和拱度弦长比fmax/c。表2为SJ系列拱线的型值表，可供后续的设计参考。

表1　SJ系列拱线攻角和拱度弦长比（CL=1.0）Tab.1　Angle of attack and camber ratio of SJ series camber lines（CL=1.0）

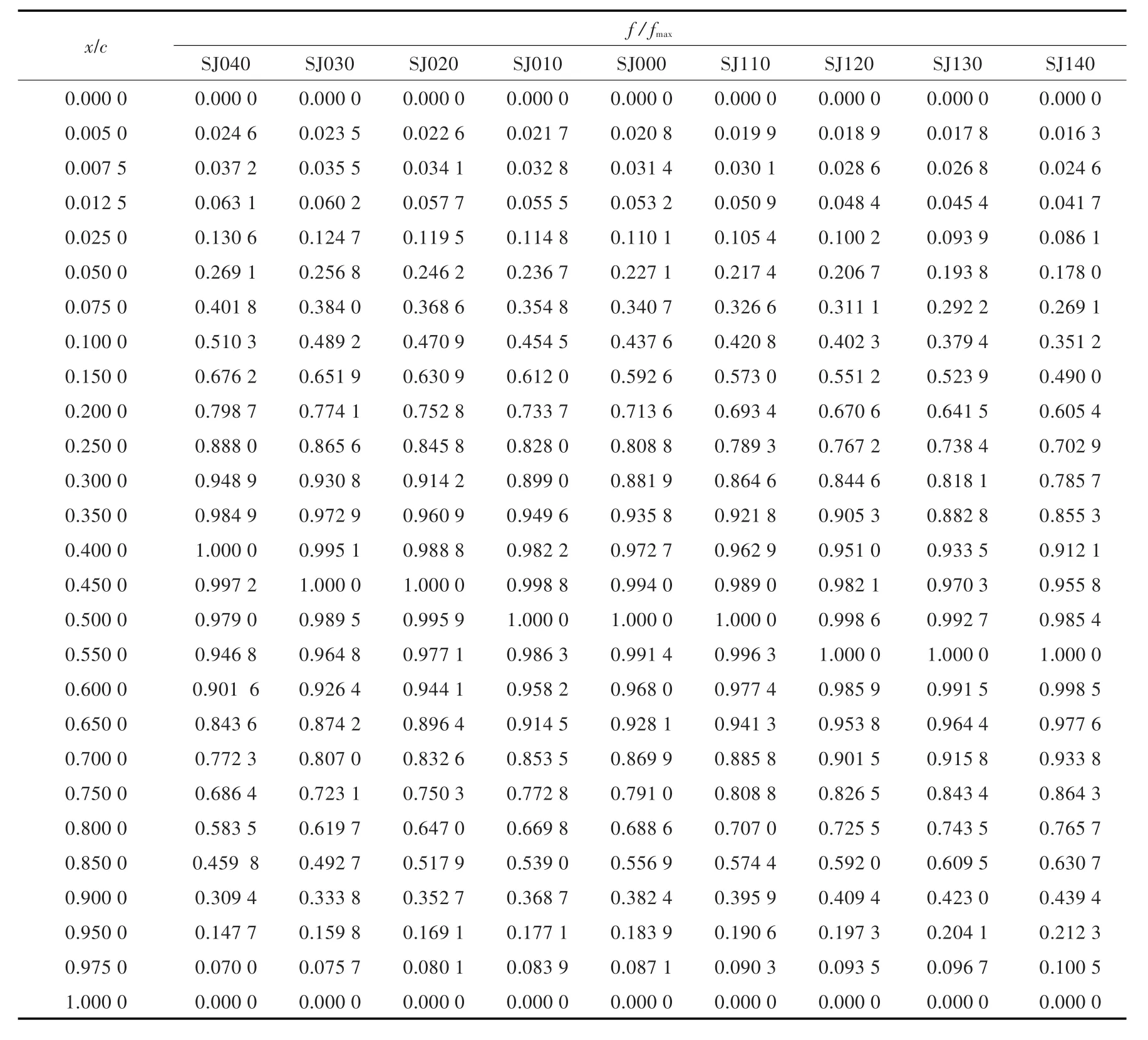
表2　SJ系列拱线型值表Tab.2　Offset table of SJ series camber lines

3　结　论

本文对螺旋桨剖面拱线的升力分布进行了定义，并提出了一种升力分布的参数化方法。采用Newton-Raphson方法设计了给定升力分布的系列拱线。主要结论和工作如下：

1）对螺旋桨剖面拱线的载荷用升力分布来表达，并提出了一种升力分布的参数化形式。

2）结合Newton-Raphson迭代方法和涡格法可以快速、精确地设计给定升力分布的拱线。

3）设计了SJ系列拱线并给出了几何型值供设计参考。

［1］ABBOTT I H，VON DOENHOFF A E.Theory of wingsections：including a summary of airfoil data［M］.Dover，DE：Dover Publications Inc.，1959.

［2］王献孚.船用翼理论［M］.北京：国防工业出版社，1998.

［3］LIGHTHILL M J.A new method of two-dimensional aerodynamic design：M2112［R］.London，UK：Aeronautical Research Council，1945.

［4］EPPLER R，SOMERS D M.A computer program for thedesignandanalysisoflowspeedairfoils：NASA-TM-80210［R］.Hampton，VA：NASA Langley Research Center，1980.

［5］EPPLER R，SHEN Y T.Wing sections for hydrofoils-part 1：symmetrical profiles［J］.Journal of Ship Research，1979，23（3）：209-217.

［6］SHEN Y T，EPPLER R.Wing sections for hydrofoils-part 2：nonsymmetrical profiles［J］.Journal of Ship Research，1981，25（3）：191-200.

［7］ 王大政，王言英，柴树红.新型叶剖面设计及叶剖面参数对空泡特性影响的研究——（1）新型叶剖面设计［J］.水动力学研究与进展，1999，14（2）：189-200.

WANG Dazheng，WANG Yanying，CHAI Shuhong. Study on a new approach to blade section design and effects of its parameters on cavitation characteristics partⅠ：a new approach to blade section design［J］.Journal of Hydrodynamics，1999，14（2）：189-200.

［8］王大政，王言英.新型叶剖面设计及叶剖面参数对空泡特性影响的研究—（2）剖面参数对空泡特性的影响［J］.水动力学研究与进展，2000，15（3）：320-328.

WANG Dazheng，WANG Yanying.Study on a new approach to blade section design and effects of its parameters on cavitation characteristics partⅡ：effects of blade section parameters on cavitation characteristics ［J］.Journal of Hydrodynamics，2000，15（3）：320-328.

［9］ ZHOU W X，WU Y H，DONG S T.A propeller design method with new blade section for improving cavitation inception under unsteady condition［J］.Journal of Ship Mechanics，2001，5（6）：18-26.

［10］SU Y M，IKEHATA M，KAI H.A numerical method for designing three-dimensional wing based on surface panel method［J］.Journal of the Society of Naval Architects of Japan，1997，182：39-47.

［11］蔡昊鹏，苏玉民，沈海龙.基于面元法的三维机翼数值设计［J］.海军工程大学学报，2009，21（6）：30-35.

CAI Haopeng，SU Yumin，SHEN Hailong.Numerical design of three-dimensional wing based on surface panel method［J］.Journal of Naval University of Engineering，2009，21（6）：30-35.

［12］谭廷寿，刘飞.非均匀流场中桨叶剖面设计方法［J］.武汉理工大学学报（交通科学与工程版），2006，30（3）：437-440.

TAN Tingshou，LIU Fei.Design method of blade section in non-uniform flow field［J］.Journal of Wuhan University of Technology（Transportation Science& Engineering Edition），2006，30（3）：437-440.

［13］李俊华，唐登海，董世汤.指定压力分布的螺旋桨设计［J］.船舶力学，2010，14（1/2）：10-19.

LI Junhua，TANG Denghai，DONG Shitang.Propeller design by prescribed pressure distribution［J］. Journal of Ship Mechanics，2010，14（1/2）：10-19.

［14］黄胜，任万龙，王超.水翼剖面多目标粒子群算法优化［J］.哈尔滨工程大学学报，2014，35（12）：1451-1457.

HUANGSheng，RENWanlong，WANGChao. Multi-objective particle swarm optimization of hydrofoil sections［J］.Journal of Harbin Engineering University，2014，35（12）：1451-1457.

［15］常欣，郭春雨，孟祥印，等.基于粒子群算法的水翼剖面优化设计［J］.船舶工程，2010，32（5）：1-3，26.

CHANG Xin，GUO Chunyu，Meng Xiangyin，et al. Design of hydrofoil section based on particle swarm optimization［J］.Ship Engineering，2010，32（5）：1-3，26.

［16］ 曾志波.最大空泡起始航速及最小空泡脉动压力螺旋桨设计［D］.北京：中国舰船研究院，2014.

［17］龙文，谢伟，杨向晖，等.基于新型剖面设计的螺旋桨多目标性能权衡优化［J］.舰船科学技术，2011，33（11）：56-60.

LONG Wen，XIE Wei，YANG Xianghui，et al. Multi-objective optimization of open water performance of propeller based on new anti-cavitation airfoil profile design［J］.Ship Science and Technology，2011，33（11）：56-60.

［18］ 饶志强，杨晨俊，李巍.基于升力分布的二维翼型设计方法［C］//2015年船舶水动力学学术会议.哈尔滨：［s.n.］，2015.

［19］ 王国强，董世汤.船舶螺旋桨理论与应用［M］.哈尔滨：哈尔滨工程大学出版社，2007.

［20］ 徐华舫，张炳暄，朱自强，等.亚、超音速定常位流的面元法［M］.北京：国防工业出版社，1981.

［21］KATZ J，PLOTKIN A.Low-speed aerodynamics ［M］.2nd ed.New York：Cambridge University Press，2001.

Camber lines design approach of propeller blade sections based on the vortex lattice method

RAO Zhiqiang1，2，YANG Chenjun1，2
1 State Key Laboratory of Ocean Engineering，Shanghai Jiao Tong University，Shanghai 200240，China
2 Collaborative Innovation Center for Advanced Ship and Deep-Sea Exploration，Shanghai 200240，China

Blade sections correlates closely with marine propeller hydrodynamic performance，including loading status，efficiency，cavitation，and other factors，and there is a direct relationship between camber lines and the loading status of blade sections.For the sake of designing camber lines of blade sections with specified loading，a lift distribution is first defined as loading description.A parametric method is then proposed for lift distribution expression，after which the camber line is designed for the specified lift distribution through Newton-Raphson iteration.Finally，the flow characteristics of camber lines are calculated with 2D vortex lattice method.The results indicate that the lift distribution of camber lines designed by combining Newton-Raphson iteration and vortex lattice method matches the given one.Furthermore，certain parameters of the lift distribution are modified to generate camber lines called SJ series for the future design.

propeller blade section；camber line design；lift distribution；vortex lattice method；SJ series camber lines

U664.33

A

10.3969/j.issn.1673-3185.2016.04.006

2015-09-30网络出版时间：2016-7-29 9:45

饶志强（通信作者），男，1986年生，博士生。研究方向：船舶推进器水动力学。

E-mail：hellostar@126.com

杨晨俊，男，1964年生，博士，教授，博士生导师。研究方向：船舶推进器水动力学。

E-mail：cjyang@sjtu.edu.cn