基于Volterra级数的水轮机调速器液压系统故障诊断

付一丁，李　穆，李丰攀，顾　然

基于Volterra级数的水轮机调速器液压系统故障诊断

付一丁1，李穆2，李丰攀2，顾然2

（1.中国长江三峡集团公司，北京 100091；
2.国网电力科学研究院武汉南瑞有限责任公司，湖北武汉 430074）

针对现有水轮机调速器液压系统故障诊断存在诸如诊断精度不高、泛化能力不强、在线检测能力不足等问题，根据Volterra级数的非线性模型高辨识能力以及可实时在线计算等优点，本文提出了一种基于Volterra级数的水轮机调速器液压系统故障诊断的新方法。该方法利用递推最小二乘法辨识出系统Volterra核，经多维广义离散Fourier变换得到系统广义频域响应函数（GFRF）模型，最后利用主元分析法（PCA）进行特征提取及分类，从而实现系统故障的高效诊断。仿真结果表明，该方法具有较高辨识精度，能准确分辨出系统的不同状态。

Volterra；广义频域响应函数（GFRF）；主元分析法（PCA）；故障诊断；调速器；水轮机

0　引言

水轮机调速系统是水轮发电系统的重要控制子系统之一，其稳定、可靠运行是整个水电机组安全、高效运行的重要条件［1］。随着近年水电站自动化水平和对水轮发电系统安全运行要求的不断提高，水轮机调速系统的故障诊断具有重要的现实意义。从长期的工程经验中归纳出水轮机调速系统的故障可分为电气、机械和液压3大类。据统计资料表明，机械和液压故障占比超过60%［2］。因此，对水轮机调速器液压系统的故障诊断成为整个水轮发电系统故障诊断的重要一环。

学者们已经对水轮机调速器液压系统的故障诊断做了一些重要的研究工作。文献［3］利用状态观测器残差的故障信息特征明显的特点，根据不同故障下残差分布的不同，识别调速器液压系统的不同故障状态。文献［4］通过对调速器液压系统故障机理的研究，利用故障树的最小割集矩阵进行故障树定性分析，确定系统故障，通过基于模型参考的方法准确定位故障，最后结合专家系统给出诊断结果。以上方法，虽然取得了一定的成就，但目前调速器液压系统故障诊断方法普遍存在故障辨识精度不高、泛化能力不强或无法实现在线诊断等问题。

为此，本文提出了基于Volterra级数的调速器液压系统故障诊断方法。该方法利用Volterra级数的非线性模型高辨识能力以及可在线实时计算等优点，通过对液压系统的输入输出采样，利用最小二乘法辨识出正常状态下以及各种故障状态下液压系统的Volterra核，进而得到不同状态下系统的广义频域响应函数（Generalized Frequency Response Functions，GFRF），基于GFRF谱提取相应特征形成特征向量，利用主元分析法（Principal Component Analysis，PCA）剥离各个特征指标之间的线性关系、降低特征向量的维度，从而最终实现系统不同状态的分类及故障诊断。

1　Volterra理论

Volterra泛函级数是由意大利数学家Vito-Volterra 于1880年首次提出的。由于这一理论具有强大的模拟非线性系统行为的能力，引起了行业内的广泛关注，不久便被应用于实际工程应用。经理论研究表明，任何的连续时不变非线性动态系统，若输入输出响应是解析函数，则该系统可以用式（1）的形式完全描述［5］。且由实践证实，绝大多数非线性系统只用有限项的形式即可满足实际应用的要求［6］。

对于一个非线性系统y（t）=f（t，u（t）），其Volterra模型被一系列卷积积分所表示为

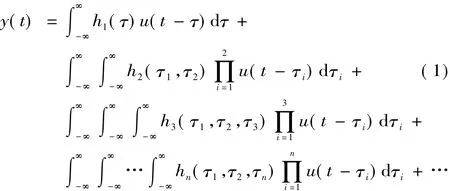
式中，积分项内的u（t）代表系统的输入；y（t）表示系统的响应。每个卷积积分内的线性函数（h1）以及非线性函数（h2，…，hn）被称为系统的Volterra核，它们表征了整个系统的动态行为。即，一阶核h1（τ）是系统输入u在时间上延时τ后的线性响应函数，二阶核h2（τ1，τ2）则反映的是系统的二次特性。依此类推，hn（τ1，τ2，…τn）作为系统的n阶核函数，它包含了系统的n阶非线性特征。根据式（1），Volterra模型的离散数学表达形式如下

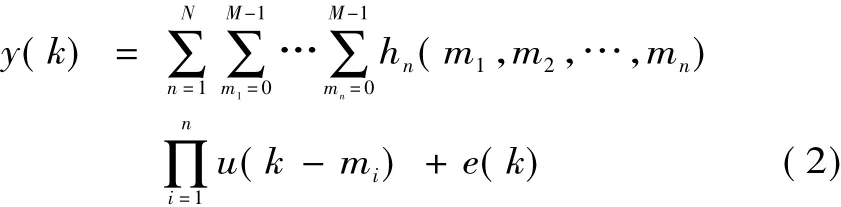
式中，N为Volterra模型最大阶数；M为记忆长度；e（k）为截断误差。只要N和M取得适当，截断误差e（k）将很小，可忽略不计。

将式（2）中的hn进行多维广义离散Fourier变换［7］，即可得到系统的n阶频域Volterra核，或称为系统的n阶广义频率响应函数（GFRF）。

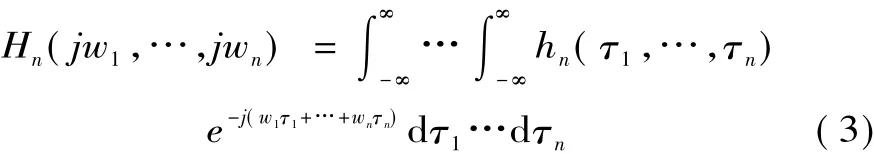
相对于脉冲响应函数描述线性系统的传递模型，Volterra的频域核则是描述系统非线性传递特性的非参数模型［8］。因此，针对不同状态下表现出的非线性传递特性的辨识，利用Volterra模型及其各阶核的GFRF频谱提取相应特征，即可分辨出当前系统所处状态。

2　Volterra故障诊断

本文利用Volterra级数进行故障诊断的整体流程如图1所示。

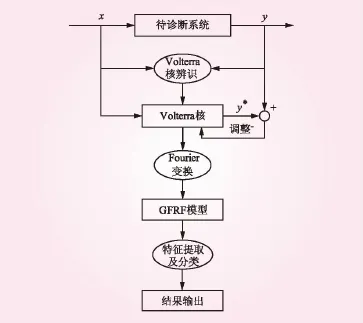
图1　Volterra故障诊断过程

如图1所示，流程的核心在于通过实时对比系统当前输出与模拟输出的偏差，动态调整Volterra核，使其更接近真实系统。待调整稳定后，再利用多维广义离散Fourier变换得到系统的GFRF模型及其各阶核的幅频特性曲线。针对所得到的幅频特性曲线提取足以表征曲线特性的参量组成特征向量，经过标准化处理后输入PCA模块，解析出主要影响因素，揭示系统的本质，简化复杂的问题，最终实现不同状态的识别。

2.1GFRF模型辨识

Volterra级数用以表示单输入单输出连续因果系统，形如式（1）。在进行系统分析时，一般用前三阶Volterra级数即可描述一大类非线性系统的动力学特性［9］。不考虑直流分量，仅保留前三阶，且利用Volterra核的对称性，式（1）可改写为

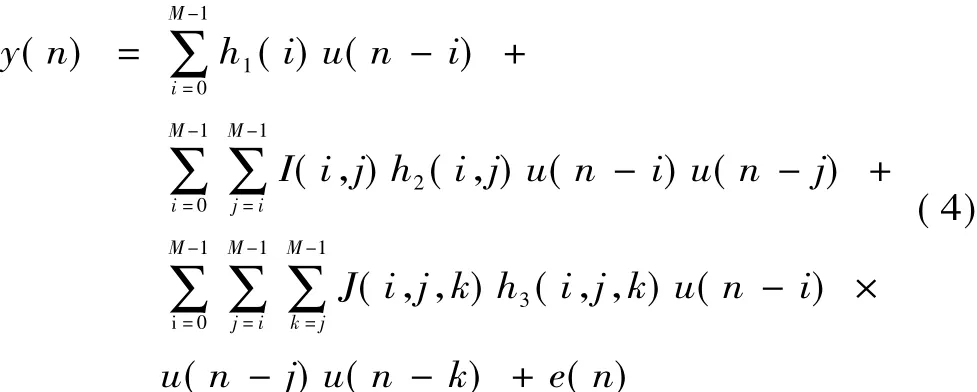
式中，M为记忆长度，e（n）为截断误差，I（i，j）=

。

定义系统的输入矩阵为X（n）=［U（n），U（n+ 1），…，U（n+L-1）］T，输出矩阵为Y（n）=［y （n），y（n+1），…，y（n+L-1）］T，Volterra核矩阵Θ=［h1（0），…，h1（M-1），h2（0，0），h2（0，1），…，h2（M-1，M-1），h3（0，0，0），h3（0，0，1），…，h3（0，0，M-1），…，h3（M-1，M-1，M-1）］。其中，L为数据长度，U（n）=［u（n），…，u（n-M+1），u2（n），2u（n）u（n-1），…，u2（n-M+1），u3（n），3u2（n）u（n-1），…，u3（n-M+1）］。式（4）可改写成矩阵的形式

从式（5）可以看出，求解Volterra核的问题可以转化为一个标准的最小二乘问题，即

本文采用递推最小二乘法（RLS）作为模型自适应辨识算法，形式如下

其中，初值P可取1 000*eye（ker_num），ker_num为核的个数。将系统输入输出实时采样数据经过多次递推后，即可得到系统的时域内Volterra核。

最终，将求得的时域内Volterra核hN（m1，m2，…，mN）经过离散时间 Fourier变换（Discrete-time Fourier Transform，DTFT）

之后即可得到系统频域内的GFRF模型。

2.2特征提取

在本文中，GFRF模型的特征提取采用目前基于多元统计过程控制的故障诊断技术的核心—主元分析法（PCA）。合理的选取各阶GFRF模型中的最优特征，是PCA计算的前提条件。文章选取了最大值，最小值，均方根作为系统GFRF模型特征指标，整个计算流程如图2所示。

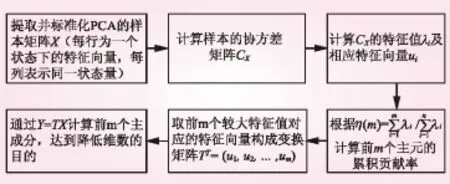
图2　PCA计算流程

3　模型仿真与实验

本章节将第3节介绍的基于Volterra级数的故障诊断方法应用到水轮机调速器液压系统，通过在仿真环境下进行试验，以验证该方法的有效性。模型的辨识采用Volterra三阶模型。

3.1模型建立

本文仿真对象为水轮机调速器液压系统，模型搭建采用Matlab的Simulink平台。水轮机调速器的液压系统主要由电液转换器、主配压阀、机械液压开度限制装置和位置反馈等部分构成［10］。本文基于文献［11］中给出的仿真系统，为了更好的模拟系统非线性特点，在模型中加入了死区环节、限幅环节和速度限制环节等非线性环节。整个模型构建如图3所示。

图3　液压系统结构示意

整个系统具有两级液压放大，其中控制信号U与接力器位移信号Yf综合后，由电液转换器带动引导阀—辅助接力器完成第一级液压放大，同时对其进行限幅（主接力器开、关机时间限制）。第一级放大输出经过死区环节（机械件连接间的空隙）后送入主配压阀—主接力器完成第二级液压放大，同时对其进行开度限制控制。

依据实际现场中常见的水轮机调速器液压系统故障［12］，此次仿真的水轮机调速器液压系统故障包括：

（1）液压阀卡涩。此种情况发生时，液压阀将不能产生正确的机械位移信号，或使接力器朝单一方向（开启或关闭）运动，或使接力器固定不动，故不能正确控制导叶（或轮叶）的动作，即

（2）接力器位置反馈信号偏移或消失。此种情况发生后，随动系统将出现误差，甚至会破坏随动系统的跟随性能，即

3.2结果及分析

液压系统模型参数选取辅助接力器反应时间常数Ty1=0.01 s，主接力器反应时间常数Ty=0.1 s，死区Sd=0，Volterra模型阶数为3，取记忆长度为18。仿真系统处于空载摆动工况，模拟该工况下输入信号如图4a所示。图4b为系统真实输出与模拟输出的对比图，两者之间的误差见图4c，从图中可表明用最小二乘辨识出的Volterra模型能够能好的还原真实系统。将辨识得到的系统Volterra核经过多维广义离散Fourier变换得到系统GFRF模型，其各阶核的幅频特性曲线如图4d～4f所示。根据Volterra理论，系统的GFRF模型在不同的状态下具有唯一性，故可以通过对比不同状态下系统一阶、二阶和三阶广义频率响应函数（H1、H2和H3）的不同来识别系统所处状态。

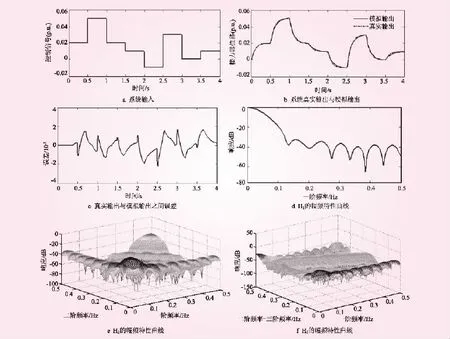
图4　正常工作状态

根据3.1小节所述的液压系统常见故障，通过仿真的方法模拟系统分别处于液压阀卡涩和接力器位置反馈信号偏移的故障状态。将图5a的信号输入上述两种系统，得到相应状态下系统的输出。利用采集的输入输出信号，经过GFRF模型辨识后得到的结果见图5、6。

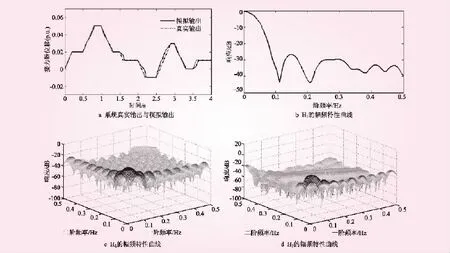
图5　液压阀卡涩状态

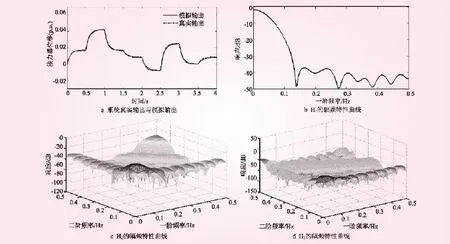
图6　接力器位置反馈信号偏移状态

对比图4～6中的H1、H2和H3的幅频特性曲线，可以看出在三种不同状态下系统GFRF模型的各阶核的幅频特性曲线具有明显的不同。H1反映的是系统的线性特征，H2和H3反映的则是系统的非线性特征。由于在仿真故障的情况下，三种不同状态下系统的线性特性均被改变，故其H1曲线的形式各有不同。另外，从输出对比图中可以看出，液压阀卡涩状态下系统的输出与正常工作状态相比有明显的非线性，故在前者的H2中可以看到其特性幅值波动较为剧烈。而在接力器位置反馈信号偏移状态与正常状态相比，其输出信号形式上基本一致只是幅值上略微减小，反映在H2中即其相对于正常工作状态的特性曲线较为平缓。再者，H3体现的则是更为复杂的非线性关系，情况与H2基本相同。于此，得到了系统的三种不同的状态下系统的GFRF模型，如何从所得到的曲线图中提取特征，让状态分类更为明显，成为下一步的重点。

GERF模型的特征提取采用PCA方法，依照3.2节所述，选取系统H1、H2以及H3的幅频响应曲线的最大值，最小值，均方根共9个特征作为该系统GFRF的特征指标，各指标数值见表1。选取输出特征维度m= 2，经过PCA后得到的新的主元特征如图7a所示。

表1　GFRF模型特征值

图7　GFRF模型的PCA方格

从图7a中可以看出，将表1中的各种不同状态下的特征向量经过PCA特征提取及分类后，以两个主元特征表示的系统的GFRF模型状态点分布在图示的矩形方格内。从图中可以看出，在3种不同的状态下状态点的分布位置的差异程度足以分辨。由于GFRF模型在某一状态下形式的唯一性，即便是同类型的故障，例如接力器位置反馈信号y偏移，假如故障发生的情况不同（例如接力器位置反馈信号偏移分别为1.2y和1.5y），在方格图中所呈现出来的状态点的位置也将不同。这就是说，图中某一状态点仅能代表一种特定的故障状态。但在通常情况下，同一类的故障的状态点在方格图中出现的位置较为接近，文中给出一例见图7b。在实际工程应用中，可先将各种典型状况的状态点确定下来，画到方格图中以备参考。应用时，将所采集的输入输出信号经过本文所述流程分析过后，状态点将会唯一的出现在方格图中的某一位置，此时工作人员可人为地判断离此状态点距离最近的典型工况即为当前系统的所处工作状态。

4　结语

本文提出了基于Volterra级数的水轮机调速器液压系统故障诊断方法。通过仿真试验获得液压系统的三种不同状态，依据每种状态的输入输出信号辨识出各种状态下系统的Volterra核，经多维广义离散Fourier变换后得到不同系统的GFRF模型，将GFRF的幅频特性曲线经过PCA特征提取后，各个不同状态分类明显，从而实现了调速器液压系统故障的快速准确诊断。

基于Volterra级数的故障诊断方法的关键在于如何求出待测系统的Volterra核，由于Volterra核数目随着阶数的增加呈几何级数增长，如何高效、快速的计算出有效核成了决定诊断过程实时性、准确性的关键。为了提高辨识效率，可以考虑利用智能算法辨识Volterra的有效核，可极大降低Volterra级数的核数目。同时，GFRF中的特征参数的自适应选取也是今后的研究重点。

［1］杜文武.基于改进遗传算法的水轮机PID调速器参数优化设计［D］.南京：河海大学，2004.

［2］孙邦彦.水轮机调速器液压系统常见故障及处理［J］.小水电，2003（4）：32-38.

［3］和一凡，张江滨.基于状态观测器的调速器液压系统故障诊断［J］.电网与清洁能源，2009，25（4）：61-64.

［4］邹波.故障树与模型参考故障诊断在水轮机调速器液压系统的应用［J］.武汉大学学报：工学版，2003，36（3B）：117-120.

［5］曹建福，韩崇昭，方洋旺.非线性系统理论与应用［M］.西安：西安交通大学出版社，2001.

［6］TANG H，LIAO Y H，CHAO J Y，et al.Fault diagnosis approach based on Volterra models［J］.Mechanical Systems and Signal Processing，2010，24（4）：1099-1113.

［7］川又政征，口龙雄.多维数字信号处理［M］.薛培鼎，徐国鼐，译.北京：科学出版社，2003.

［8］魏瑞轩，韩崇昭，张优云，等.非线性系统故障诊断的Volterra模型方法［J］.系统工程与电子技术，2004，26（11）：1736-1738.

［9］张华君.基于递推批量最小二乘的Volterra级数辨识方法［J］.小型微型计算机系统，2004，25（12）：2282-2285.

［10］魏守平.水轮机调节［M］.武汉：华中科技大学出版社，2009.

［11］太军君，刘长青，杨晓红.全数字水轮机调速器电液随动系统的仿真研究［J］.水力发电，2003，11：41-43.

［12］李朝辉，郭江.调速器液压系统的故障诊断及可靠控制策略［J］.水电能源科学，1999，17（3）：40-43.

（责任编辑高瑜）

Application of Fault Diagnosis Approach Based on Volterra Series for Hydraulic System of Turbine Governor

FU Yiding，LI Mu，LI Fengpan，GU Ran
（1.China Three Gorges Corporation，Beijing 100091，China；2.State Grid Electric Power Research Institute Wuhan NARI Co.，Ltd.，Wuhan 430074，Hubei，China）

At present，there are some problems in fault diagnosis of hydraulic system of hydraulic turbine governor，such as poor model identification ability，low generalization ability and limited on-line detection ability.By using the high identification ability in nonlinear model and the on-line calculation ability of Volterra series，a new fault diagnosis method is put forward. Firstly，the method uses the recursive least-squares to identify the Volterra kernel of system.Secondly，the Discrete-time Fourier Transform（DTFT）is applied to gain the Generalized Frequency Response Functions（GFRF）model of system. Finally，the characteristics which being extracted from the GFRF are pushed into Principal Component Analysis（PCA）module to classify the different status of system in a coordinate grid map.The simulation results show that this method has a clear process，a powerful adaptable ability and strong identification ability，which can accurately distinguish different system status.

Volterra；Generalized Frequency Response Functions（GFRF）；Principal Component Analysis（PCA）；fault diagnosis；governor；turbine

TV136

A

0559-9342（2016）02-0064-06

2015-08-01

付一丁（1985—），男，湖北赤壁人，工程师，硕士，主要从事水电站运行管理工作.