基于集合经验模态分解和支持向量机的大坝变形预测方法
卢献健,晏红波,梁月吉
基于集合经验模态分解和支持向量机的大坝变形预测方法
卢献健1,2,晏红波1,2,梁月吉1
(1.桂林理工大学测绘地理信息学院,广西桂林 541004;2.广西空间信息与测绘重点实验室,广西桂林541004)
受水位、温度等诸多因素共同影响,大坝变形具有随机性和非线性特征,提出了一种基于集合经验模态分解(EEMD)和支持向量机(SVM)的大坝变形预测算法。算法先对大坝位移序列进行集合经验模态分解,有效分离出隐含在时序中的非线性高频波动成分和低频趋势成分;其次根据各分量特点构造不同的SVM进行预测,最后叠加各分量预测值得到预测结果。与BP神经网络模型及传统支持向量机的对比结果表明,所提预测算法具有较强的自适应预测能力,预测精度较高。
大坝变形预测;集合经验模态分解;支持向量机;精度评定
大坝变形往往受水位、温度、自身物理变化等诸多因素共同影响,难以建立较为准确的形变量与影响因素之间的复杂非线性关系模型,因此传统时间序列法和回归分析等方法在变形预测中的应用受到了限制。经验模态分解(Empirical Mode Decomposition,EMD)是一种有效的处理非线性和非平稳信号的自适应分解方法[1]。它不需要确定任何基函数,依据信号本身的时间尺度直接对信号进行平稳化处理,“筛选”出原信号的波动项和趋势项[2]。目前,EMD算法已在众多领域得到了有效的验证和应用。戴吾蛟[3]将EMD方法应用于GPS多路径效应的探测中并取得较好的效果。罗飞雪等[4]通过实验证明了利用EMD将变形序列分解成不同特征尺度的平稳窄带信号的可行性。张豪[5]将EMD方法成功应用于大坝变形预测。然而,在信号分解过程中,EMD方法根据信号的极值点采用三次样条插值函数拟合以获得的上、下包络线存在边界效应等问题,这使分解得到的各个分量的精度受到了影响,不利于分析隐含在信号中的信号变化特征[6]。集合经验模态分解(Ensemble Empirical Mode Decomposition,EEMD)[6-7]对经验模态分解的尺度混合问题进行了优化,使经验模态分解的边界效应问题得到了有效解决。
另一方面,各种人工智能算法得到快速发展,其中支持向量机(Support Vector Machine,SVM)[8]在非线性、高维模式识别中具有独特优势而得到了广泛应用[9-11]。张卫国等[12-13]将支持向量机应用于变形预测中,解决了多因素影响下的复杂变形预测问题,取得了较好的预测效果。
基于上述研究,本文采用集合经验模态分解与支持向量机相结合的思路,对大坝变形进行分析研究。在利用EEMD对大坝序列进行分解的基础上,利用SVM对各个分量进行预测,最后叠加得到大坝变形的预测结果。
1 集合经验模态分解与支持向量机预测模型
1.1集合经验模态分解基本原理
设Y(t)为大坝变形序列,EMD分解首先搜索原始信号Y(t)的极大值、极小值来构造信号的上、下包络线Vmax(t)和Vmin(t),将原始信号与包络线均值进行比较
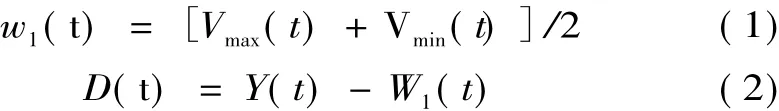
并判断D(t)是否满足构成本征模态分量(Intrinsic Mode Function,IMF)的两个条件。满足则作为第1 个IMF,否则作为新的Y(t)继续进行分解。按上述方法从高频到低频的顺序依次对信号进行分解,直到分解的余量Bn(t)是一个单调函数时结束,最终原信号可以表示为

式中,Li(t)为第 i次分解得到的本征模态分量;Bn(t)为经n次分解后的剩余分量。
由于变形序列的端点不一定处于极大值或极小值,因此所计算的上、下包络线在两端有可能偏离实际值,最终引起IMF模式混淆问题,影响EMD分解质量。
集合经验模态分解是EMD方法的改进,其利用高斯白噪声具有均匀分布、均值为0的统计特性,通过多次向原信号加入不同的随机白噪声来改变信号的极值点特性,把多次分解得到了IMF求取平均来有效解决EMD的边界效应问题[7]。EEMD分解步骤为:①向大坝监测信号序列Y(t)加入随机白噪声nm(t)得到Ym(t),其中,nm(t)要服从(0,(αε)2)的正态分布,α为噪声的强度参数,ε为信号的标准差。②使用EMD对Ym(t)进行分解,得到若干个本征模态分量Li(t)和一个剩余分量Bn(t)。③重复执行①、②共m次,其中每一次加入的白噪声序列的幅值不同。④对总计为m次EMD分解得到的每一个IMF计算均值,作为EEMD方法得到的大坝原始序列最终分量IMF。
EEMD分解结果的质量主要受EMD分解的重复次数与加入噪声的强度两因素的综合影响,但通过多次分解以及求和取平均后可以使得IMF的模式混淆问题得到有效改善。
1.2网格算法优化支持向量机
对已知训练集M={(x1,y1),…,(xk,yk)},x∈R,y∈R,k为样本总数,SVM通过映射z=φ(x)把低维不可分的样本作非线性变换为线性可分的高维特征空间E,并在空间E中建立学习机对样本的非线性特征进行线性分析或回归。其应用核函数的展开定理有效避免非线性变换中产生的“维数灾难”问题。设u,v分别为原空间D中的两个向量,根据泛函数有关理论,定义一个满足Mercer条件的对称函数k(u,v),则不难得到k(u,v)=φ(u)φ(v)。这样,通过在高维空间计算内积,不考虑高维空间的维数,就可以实现非线性向高维线性的转变,建立支持向量机回归模型[9]

式中,αi、βi均为 Lagrange因子;Δ为常数项;k(xxi)为核函数。
实际应用中,SVM的性能取决于所选用的核函数。而多项式核函数、径向基核函数(RBF),和sigmoid核函数是SVM常采用的3种核函数。本文以径向基核函数为SVM的核函数,其关键是确定核函数k(xxi)中最优的惩罚参数C和核参数g,参数C、g的选择是否合理直接对SVM的预测精度产生影响。本文利用网格搜索法进行参数寻优[15],通过设定参数C、g的取值范围并格网化,利用交叉验证方法计算网格内各组合参数的训练均方根误差,并取最小均方根误差对应的C和g作为参数寻优结果。
1.3EEMD-SVM预测模型流程
基于EEMD-SVM的大坝预测模型,将大坝在各个时间点的变形值作为一时间序列{X(t),t=1,2,…,m},对序列X(t)进行集合经验模态分解得到n个本征模态函数IMF和1个残差项B,即
X(t)=B+IMF1+IMF2+…+IMF(n)(5)对各个IMF和B使用网格搜索寻找最优的径向基核函数参数C、g,并建立各自的SVM预测模型进行预测,通过预测得到各分量的预测值YIMF1,YIMF2,…,YIMF(n)和YB,最后将各分量预测值叠加得到大坝变形预测结果Y为

综上所述,建立EEMD-SVM大坝变形预测模型的方法与流程见图1所示。

图1 模型预测流程
2 预测精度评定

为综合评定预测结果的精度,本文采用均方根误差和平均绝对值误差作为模型预测结果精度的评定指标,即式中,MSE为均方根误差;MAE为平均绝对误差;Yt为大坝实际变形值;Y^t为大坝预测值;n为大坝观测期数;t为大坝观测第t期。
3 算例分析
为了分析验证本文模型的有效性及精度,以某钢筋混凝土重力坝[16]为例,选择其具有代表性的第30号坝段共91期的坝顶水平位移进行数据分析,其水平位移变形如图2所示。由图2可知,该大坝的水平位移变形随机性变化较强,呈非线性变化趋势。

图2 大坝变形水平位移序列
利用本文的EEMF-SVM预测模型对以上变形序列进行预测。首先,采用EEMD对大坝变形序列进行分解,其结果中各分量如图3所示。

图3 EEMD分解结果
图3表明,EEMD将大坝序列分解为5个IMF 和1个余量B,5个IMF分量的频率逐级降低,表示了不同因素影响下的波动特征,余量B属于低频成分,代表了原变形序列中随时间变化的趋势。其中,分量IMF1~IMF3的信号周期性波动的特点较明显,而这个波动的周期并不稳定,具有非均匀变化的特性。这种非均匀变化反映了大坝水位、温度及坝体结构变化等内外部因素共同作用的非线性。可见,经EEMD分解后各IMF分量更加明显的反映了隐含在时序中的物理特征,各分量变化曲线比原变形序列曲线(图2)光滑和平稳,有利于变形分析与预报。
分解后,IMF和B分量序列的数据个数均为91个,选取第1~71个样本作为训练样本,其余样本作为测试样本。分别使用支持向量机对分解得到的各分量进行训练和预测,其中核函数均选用径向基核函数,利用网格搜索法对惩罚参数C和核参数g进行寻优,各分量的模型参数寻优结果见表1。
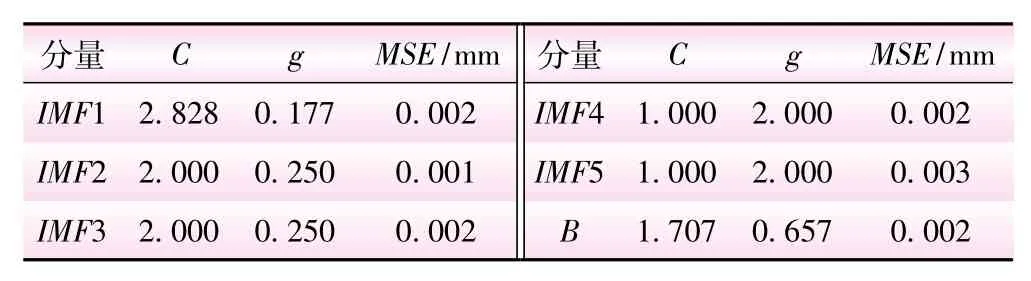
表1 各个分量SVM预测模型参数
为了进行比较,同时利用BP神经网络模型和传统支持向量机(SVM)模型进行预测。3种方法的变形预测结果对比见表2,图4直观地反映了各模型预测结果和大坝实际变形的对比。
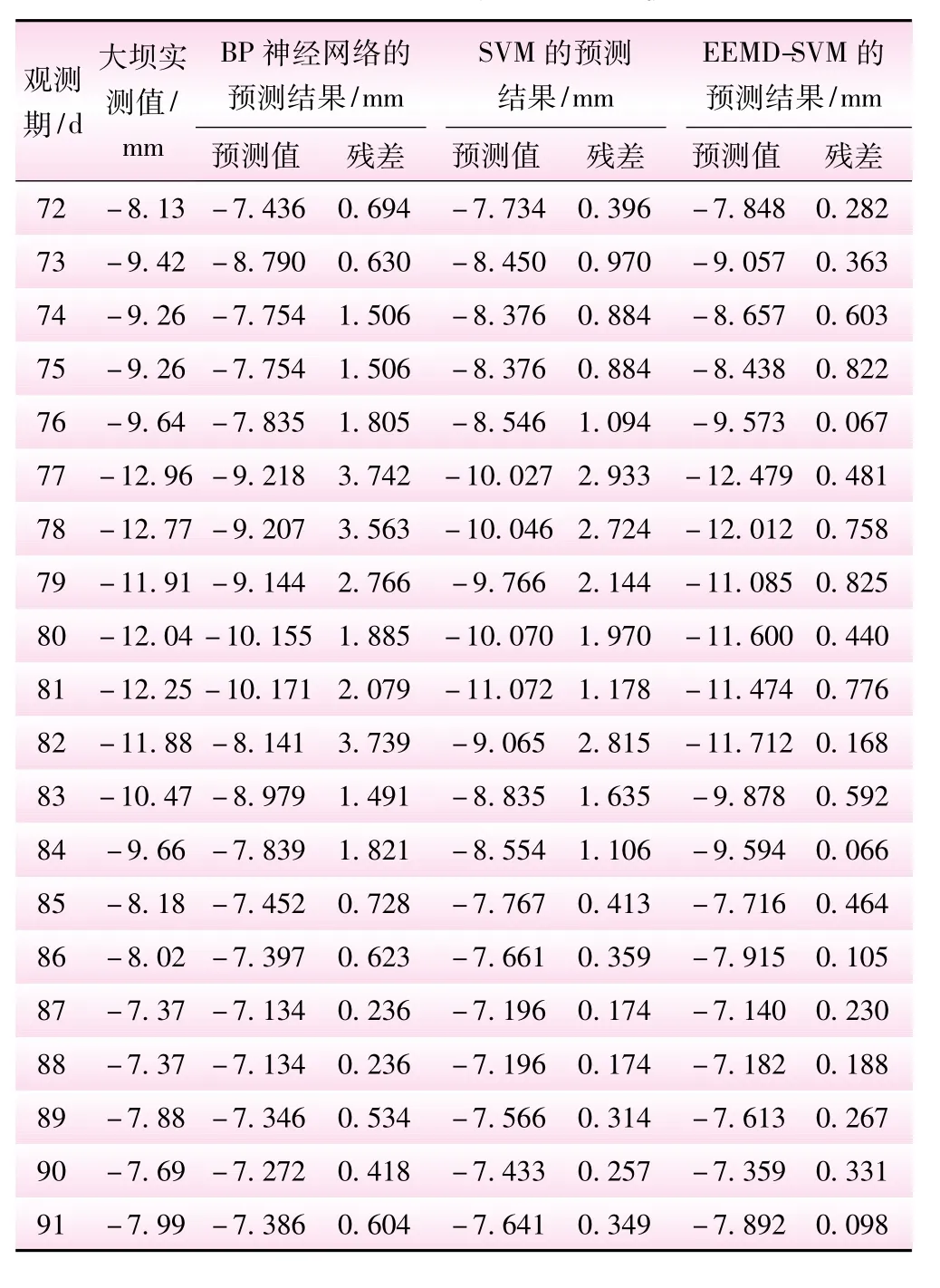
表2 不同方法的预测结果比较 mm
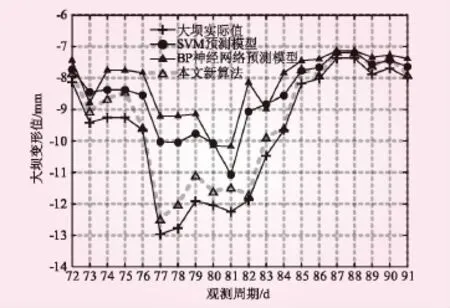
图4 各模型的预测值和大坝实际变形值对比
由表2可见:BP神经网络和传统支持向量机的预测结果相近,部分预测值和实际值相差比较大,预测结果的最大残差分别为3.742、2.933 mm。而本文算法的预测值和残差均优于其他预测模型,残差最小值为0.067 mm,最大值仅为0.825 mm。从图4可进一步看出,在大坝变形浮动大的第74~84期,BP神经网络和传统的支持向量机在预测中都出现了不同程度的偏差,而本文算法的预测结果则比较稳定,也更接近于大坝实际值;在大坝变形较平稳的第85~91期,各模型预测结果较好地与实际值相符合。
为评定模型预测精度,根据3种方法的预测结果计算了各自的均方根误差和平均绝对误差两项精度指标,其结果如表3所示。可知,本文EEMDSVM模型的预测精度优于传统SVM模型和BP神经网络模型,具有较好的全局预测精度。

表3 各预测模型精度对比 mm
4 结论
本文将EEMD和SVM相结合并应用于大坝变形预测。算例的分析结果表明,EEMD能够将复杂、非线性的大坝变形序列分解为不同特征尺度的平稳信号,有效分离出大坝变形序列中不同频率的波动和趋势成分;利用SVM对这些“单纯”的平稳信号分别建立SVM预测模型,则更有利于支持向量机性能的充分发挥,最终提高预测结果的精度。与传统SVM模型和BP神经网络模型的比较结果表明本文EEMD-SVM模型更有优势,对大坝、边坡监测等工程领域具有一定的参考意义。
[1]HUANG N E,SHEN Z,LONG S R,et al.The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J].Proceedings of the Royal Society of London A,1998,454(1971):903-995.
[2]张恒璟,程鹏飞.基于经验模态分解的CORS站高程时间序列分析[J].大地测量与地球动力学,2012(3):129-134.
[3]戴吾蛟,丁晓利,朱建军,等.基于经验模态分解的滤波去噪法及其在GPS多路径效应中的应用[J].测绘学报,2006,35(4):321-327.
[4]罗飞雪,戴吾蛟.小波分解与EMD在变形检测应用中的比较[J].大地测量与地球动力学,2010,30(3):137-141.
[5]张豪,许四法.基于经验模态分解和遗传支持向量机的多尺度大坝变形预测[J].岩石力学与工程学报,2011(S2):3681-3688.
[6]毛玉龙,范虹.经验模式分解回顾与展望[J].计算机工程与科学,2014,36(1):155-162.
[7]WU Z,HUANG N E.Ensemble empirical mode decomposition:a noise-assisted data analysis method[J].Advances in Adaptive Data Analysis,2009,1(1):1-41.
[8]MONFARED M,RASTEGAR H,KOJABADI H M.A new strategy for wind speed forecasting using artificial intelligent methods[J].Renewable Energy,2009,34(5):845-848.
[9] CORTES C,VAPNIK V.Support vector networks[J].Machine Learning,1995,20(3):273-297.
[10]张卫国,钟平安,张玉兰,等.季节性支持向量机中长期径流预报模型[J].水力发电,2014,40(4):17-21.
[11]姜振翔,徐镇凯,彭圣军,等.基于贝叶斯支持向量机的溃坝生命损失风险评价方法[J].水力发电,2014,40(4):31-34.
[12]章永来,史海波,周晓锋,等.基干统计学习理论的支持向量机预测模型[J].统计与决策,2014(5):72-74.
[13]肖浩波,谷艳昌.混凝土坝安全监控最小二乘支持向量机模型[J].长江科学院院报,2013,30(5):34-37.
[14]王新洲,范千,许承权,等.基于小波变换和支持向量机的大坝变形预测[J].武汉大学学报:信息科学版,2008,3(5):469-471.
[15]LIU Xianglou,JIA Dongxu,LI Hui.Research on Kernel Parameter Optimization of Support Vector Machine in Speaker Recognition[J]. Science Technology and Engineering,2010,10(7):1669-1673.
[16]姜成科.基于遗传算法的神经网络在大坝变形预报中的应用[D].大连:大连理工大学,2009.
(责任编辑王琪)
Dam Deformation Prediction Method Based on Ensemble Empirical Mode Decomposition and Support Vector Machine
LU Xianjian1,2,YAN Hongbo1,2,LIANG Yueji1
(1.College of Geomatics and Geoinformation,Guilin University of Technology,Guilin 541004,Guangxi,China;2.Guangxi Key Laboratory of Spatial Information and Geomatics,Guilin 541004,Guangxi,China)
Affected by water level,temperature and other factors,the deformation of dam is random and nonlinear.A new algorithm based on Ensemble Empirical Mode Decomposition(EEMD)and Support Vector Machine(SVM)for dam deformation prediction is presented herein.First,the deformation sequence is decomposed by EEMD in order to effectively separate the nonlinear trend of high frequency component volatility and low frequency component.Then,the SVM is applied to build a prediction model for each component.Finally,the predicted values of each component are superimposed.The calculation result is analyzed and compared with the results of BP neural network and traditional SVM.The comparison shows that the new algorithm has stronger ability of adaptive fitting prediction and the prediction accuracy is higher.
dam deformation prediction;empirical mode decomposition;support vector machine;precision evaluation
TV698.11
A
0559-9342(2016)02-0038-04
2015-05-12
国家自然科学基金资助项目(41161072);广西空间信息与测绘重点实验室基金项目(13-051-14-09、13-051-14-15)
卢献健(1982—),男(壮族),广西南宁人,讲师,硕士,主要从事GNSS应用、精密工程测量;晏红波(通讯作者).

