具有依赖开工时间恶化工件的流水作业排序问题研究综述
王吉波,郭苗苗,刘 桓,李 琳,王 丹
(1.沈阳航空航天大学 经济与管理学院,沈阳 110136; 2.沈阳航空航天大学 理学院,沈阳 110136;3.辽宁省体育学校 教务科,沈阳 110179; 4.沈阳航空航天大学 计算机学院,沈阳 110136)
名家综述
具有依赖开工时间恶化工件的流水作业排序问题研究综述
王吉波1,2,郭苗苗1,刘桓3,李琳2,王丹4
(1.沈阳航空航天大学 经济与管理学院,沈阳 110136; 2.沈阳航空航天大学 理学院,沈阳 110136;3.辽宁省体育学校 教务科,沈阳 110179; 4.沈阳航空航天大学 计算机学院,沈阳 110136)
具有恶化工件的排序问题是制造业、运筹学、管理科学与工程中的一类重要问题,在钢铁工业、塑料工业、军事以及医疗等方面有着广泛的应用。分析了带有依赖开工时间恶化工件的流水作业排序问题的特点,目标函数主要包括时间表长、总完工时间、总加权完工时间、最大延误、总延误时间等。然后就带有依赖开工时间恶化工件流水作业排序问题进行了全面的综述,并指出了存在的不足和许多尚未解决的问题。最后,提出了具有恶化工件的流水作业排序工作进一步研究的问题。
排序;流水作业;恶化工件
二十世纪初,全球制造业迅速发展,很多企业面临着一个共同的问题,即如何统筹安排各部门的生产从而在现有的生产条件下获得最大的产出,排序(又称调度、排程或时间表)理论应运而生。排序问题是一类重要的组合最优化问题,早期源于机器制造业,现在已逐渐发展成为运筹学、控制科学、管理科学与工程、系统科学和计算机科学等多个学科领域的交叉学科,它在生产作业安排、工程进度的控制、制造业工厂的最优设计等方面有着深刻的实际背景和广阔的应用前景(唐恒永和赵传立[1],唐国春等[2],Pinedo[3],Gawiejnowicz[4],唐国春[5-6])。
在经典的排序问题中,通常假设工件的加工时间为常数。但在某些实际问题中,工件的加工时间可能与工件的开工时间有关,由此产生具有恶化工件(deteriorating job)的排序问题,即工件的加工时间随着开工时间的延后而增大,这类问题在钢铁工业、塑料工业、军事、医疗及物流和供应链管理等方面有着广泛的应用。如在军事方面,当天气渐渐变坏或者天色渐渐变黑时,目标探测开始的时间越晚则所花费的时间就越长;在消防工程中,救火的开始时间一旦被耽搁,火势就会难以控制,这样救火的时间将会变长,所付出的代价也会变大。再比如,在钢铁制造企业的连铸-轧制生产过程中,炼钢的基本单元是炉次,它是指同一座转炉一次共同冶炼的钢水。在炼钢的连铸阶段,高温熔融钢水在连铸机底部连续凝固成钢坯。当等待时间增加时(即加工开始时间延后),在连铸机上加工的炉次的温度将会降低,从而造成炉次加工时间的恶化(刘鹏等[7])。近几年,关于恶化工件的问题得到了越来越多的关注,也取得了很多的研究成果(Gupta和Gupta[8],Browne和Yechiali[9],Mosheiov[10],赵传立等[11],Wang等[12],Wang等[13],王吉波等[14])。在另一方面,流水作业排序广泛存在于工业生产中,它是许多实际流水线生产排序问题的简化模型(Framinan等[15],Ruiz 和 Maroto[16],Emmons和Vairaktarakis[17],Fernandez-Viagas和Framinan[18])。具有恶化工件的流水作业排序问题大多数是NP-难问题,同时由于依赖开工时间的流水作业排序问题有着深刻的实际背景与广阔的应用前景,因此,深入研究依赖开工时间的流水作业排序问题,对于排序理论的发展与实际问题的解决都具有重要的意义。本文介绍了具有依赖开工时间恶化工件的流水作业排序问题,总结了相关研究的成果和特点,重点综述了具有正则目标函数的流水作业排序问题。最后,指出了存在的不足及进一步研究的问题和方向。
1 问题描述
具有依赖开工时间恶化工件流水作业排序问题可描述为:设有n个工件N={J1,J2,…,Jn}依次要在m台机器M={M1,M2,…,Mm}上进行加工,在任何时刻一台机器只能加工一个工件,工件加工过程不允许中断,在每台机器上工件的加工顺序相同,即排列排序(permutation scheduling)。工件Jj在机器Mi上的工序记为Oij,一般恶化函数假定工序Oij的实际加工时间为
pij(t)=aij+fij(t),
(1)
其中aij≥0为工序Oij的基本加工时间,fij(t)为工序Oij的任意非负函数,i=1,2,…,m,j=1,2,…,n,t为工序Oij的开始加工时间。如果fij(t)=bijt,则得一般线性恶化函数,即工序Oij的实际加工时间为
pij(t)=aij+bijt ,
(2)

下面我们给出一些概念。
优势机:对于机器Mr和Mk,如果max{arj∶1≤j≤n}≤min{akj∶1≤j≤n}(或max{brj∶1≤j≤n}≤min{bkj∶1≤j≤n}),则称机器Mk优于机器Mr,可以简写为Mk>Mr。这样我们可以定义系列优势机器:
(a)机器M1,M2,…,Mm组成递增列优势机(idm),即M1 (b)机器M1,M2,…,Mm组成递减列优势机(ddm),即M1>M2>…>Mm; (c)机器M1,M2,…,Mm组成递增-递减列优势机(idm-ddm),即 M1 (d)机器M1,M2,…,Mm组成递减-递增列优势机(ddm-idm),即 M1>M2>…>Mh (e)机器M1,M2,…,Mm组成递增-递减-递增列优势机(idm-ddm-idm),即 M1 (f)机器M1,M2,…,Mm组成递减-递增-递减列优势机(ddm-idm-ddm),即 M1>M2>…>Mh 机器无空闲(no-idle):加工工件的机器不允许在两个相邻的工件间有空闲。 工件不等待(no-wait):被加工的工件不允许在两台相邻的机器间等待。 本节主要考虑目标函数为时间表长(makespan)的排序问题,时间表长也称加工时间全长或最大完工时间,代表着机器使用效率的高低。 2.1两台机器情况 Kononov和Gawiejnowicz[19]证明了问题F2|pij(t)=aij+bijt|Cmax是强NP-难的。 Kononov[20]与Mosheiov[21]同时应用Johnson算法(Johnson[22])证明了问题F2|pij(t)=bijt|Cmax能够在O(nlogn)时间内解决,并给出了求解算法。 赵传立等[23]证明了问题F2|pij(t)=bij(A+Bt)|Cmax能够应用Johnson算法在O(nlogn)时间内解决,并给出了求解算法。 Lee等[24]研究了所有工件的恶化率都相等的具有2台机器的问题F2|pij(t)|=aij+bt|Cmax,他们给出了分支定界算法和3个启发式算法来求解这个问题。 Zhao和Tang[25]研究了具有2台机器的问题F2|pij(t)=bijt,chains|Cmax,其中chains表示工件间具有链优先约束。他们证明了对一种机器独立的链优先约束(type 1链优先约束)问题是多项式时间可解的,同时他们证明了对另一种机器独立的链优先约束(type 2链优先约束)问题是NP-难的。 2.2三台机器情况 Kononov[20]研究了具有简单线性恶化的3台机器的流水作业的排序问题,证明了问题F3|pij(t)=bijt|Cmax是强NP-难的。同样,Mosheiov[21]证明了问题F3|pij(t)=bijt|Cmax是一般NP-难的。对于问题F3|pij(t)=bijt|Cmax,即使在第一台机器M1与第三台机器M3的恶化率相同,即bi1=bi3=b,也很难提出近似算法。Kononov和Gawiejnowicz[19]研究了问题F3|pij(t)=bijt,bi1=bi3=b|Cmax,结果表明:除了在P=NP的情况下,不存在最坏情况界为常数的多项式时间近似算法。 Wang等[26]研究了三台机器的流水作业排序问题F3|pij(t)=bijt|Cmax,他们证明一些特殊情况,即问题F3|pij(t)=bijt,M1>M2|Cmax,F3|pij(t)=bijt,M3>M2|Cmax,F3|pij(t)=bijt,M2>M1|Cmax,F3|pij(t)=bijt,M2>M3|Cmax,都是多项式时间可解的,并对一般问题F3|pij(t)=bijt|Cmax,给出了分支定界算法和一个启发式算法。 Wang和Wang[27]研究了三台机器的流水作业排序问题F3|pij(t)=aij+bt|Cmax,他们给出一些优势性质和下界,从而给出了分支定界算法。为了克服分支定界算法慢的特性,他们也提出了二个启发式算法,并用数值算例说明了分支定界算法处理的问题规模和启发式算法的效果。 Wang和Wang[28]研究了三台机器的流水作业排序问题F3|pij(t)=bij(A+Bt)|Cmax,他们证明一些特殊情况,即问题F3|pij(t)=bij(A+Bt),M1>M2|Cmax,F3|pij(t)=bij(A+Bt),M3>M2|Cmax,F3|pij(t)=bij(A+Bt),M2>M1|Cmax,F3|pij(t)=bij(A+Bt),M2>M3|Cmax都是多项式时间可解的,并对一般问题F3|pij(t)=bij(A+Bt)|Cmax给出了分支定界算法和一个启发式算法。 2.3m台机器情况 赵传立等[23]研究了m台机器的流水作业排序问题Fm|pij(t)=bij(A+Bt)|Cmax,证明了当所有工件在每台机器上的恶化率都相等时(即bij=bj,j=1,2,…,n),问题Fm|pij(t)=bij(A+Bt),bij=bj|Cmax是独立于工件排列顺序的,即任意排序都是最优排序。 赵传立等[30]研究了m台机器的流水作业排序问题Fm|pij(t)=bijt,β|Cmax,其中β∈{idm,ddm,idm-ddm}。他们对这三种特殊情况分别给出了多项式时间算法。 Wang和Xia[31]研究了m台机器的流水作业排序问题Fm|pij(t)=bijt,β|Cmax,其中β∈{idm,ddm,idm-ddm,ddm-idm}。他们对一些工件不等待(no-wait)情况、机器无空闲(no-idle)情况和一般(没有工件不等待和机器无空闲限制)情况(即Fm|pij(t)=bijt,no-wait,β|Cmax,其中β∈{idm,ddm,idm-ddm},和Fm|pij(t)=bijt,no-idle,β|Cmax,其中β∈{idm,ddm,idm-ddm,ddm-idm}),分别给出了多项式时间算法。 Wang和Xia[32]研究了与Wang和Xia[31]类似的问题,只是Wang和Xia[31]研究的是成比例恶化函数(即aij=kbij)。对问题Fm|pij(t)=kbij+bijt,β|Cmax,其中β∈{idm,ddm,idm-ddm,ddm-idm}得到了与Wang和Xia[31]类似的结论。 Cheng等[33]研究了问题Fm|pij(t)=aij+bt,no-idle,β|Cmax,其中β∈{idm,ddm,idm-ddm,ddm-idm}。他们对机器满足优势关系的特殊情况(即β∈{idm,ddm,idm-ddm,ddm-idm}),分别给出了多项式时间算法。 潘明和赵传立[34]研究了问题Fm|pij(t)=aij+bt,no-idle,β|Cmax,其中机器满足优势关系β∈{idm-ddm-idm,ddm-idm-ddm}。他们对这两种特殊情况分别给出了多项式时间算法。 Sun等[35]研究了同Cheng等[33]一样的问题(即问题Fm|pij(t)=aij+bt,no-idle,β|Cmax,其中β∈{idm,ddm,idm-ddm,ddm-idm}),他们用反例说明了Cheng等[33]中的一些结论是不正确的,并给出了修正过的相关结论。 Ng等[36]研究了问题Fm|pij(t)=aij+bt,β|Cmax,其中β∈{idm,ddm,idm-ddm,ddm-idm,no-wait,no-idle}。他们对一些工件不等待情况、机器无空闲情况和一般(没有工件不等待和机器无空闲限制)情况(即问题Fm|pij(t)=aij+bt,β|Cmax,其中β∈{idm,ddm,idm-ddm},Fm|pij(t)=aij+bt,no-wait,β|Cmax,其中β∈{idm,ddm,idm-ddm},和Fm|pij(t)=aij+bt,no-idle,β|Cmax,其中β∈{idm,ddm,idm-ddm,ddm-idm}),分别给出了多项式时间算法。 Sun等[37]研究了所有工件的基本加工时间都相等的流水作业排序问题Fm|pij(t)=a+bijt,β|Cmax,其中β∈{idm,ddm,idm-ddm,ddm-idm,no-wait,no-idle}。他们对一些特殊情况(即问题Fm|pij(t)=a+bijt,β|Cmax,其中β∈{idm,ddm,idm-ddm},Fm|pij(t)=a+bijt,no-wait,β|Cmax,其中β∈{idm,ddm,idm-ddm},和Fm|pij(t)=a+bijt,no-idle,β|Cmax,其中β∈{idm,ddm,idm-ddm,ddm-idm}),分别给出了多项式时间算法。 Wang[38]研究了m台机器的流水作业排序问题Fm|pij(t)=bijt,β|Cmax,其中β∈{M1>M2>…>Mm-1,M2>…>Mm-1>Mm,M1 Yin和Kang[39]研究了m台机器的流水作业排序问题Fm|pij(t)=bij(A+Bt),β|Cmax,其中β∈{M1>M2>…>Mm-1,M2>…>Mm-1>Mm,M1 表1 时间表长目标函数Cmax 本节主要考虑目标函数为总完工时间(也称完工时间和)的排序问题,总完工时间代表着所有工件的加工时间成本。 3.1两台机器情况 Wang等[40]和Shiau等[41]分别研究了具有2台机器的问题F2|pij(t)=bijt|∑Cj,Wang等[40]证明了问题F2|pij(t)=bijt|∑Cj的一些特殊情况(即问题F2|pij(t)=bijt,b2j=b|∑Cj,F2|pij(t)=bijt,M1 Wu和Lee[42]研究了所有工件的恶化率都相等的具有2台机器的问题F2|pij(t)=aij+bt|∑Cj,此问题是NP-难得,他们给出了分支定界算法和3个启发式算法及一个改进算法来求解这个问题。 Ng等[43]研究了问题F2|pij(t)=bij(A+Bt)|∑Cj,此问题是NP-难得,他们给出了一些优势性质,4个下界和一个启发式算法作为上界,从而可用分支定界算法来求解这个问题,数值模拟说明了分支定界算法能在合理的时间内处理n=15的规模问题。 Cheng等[44]研究了具有2台机器的双目标问题,即问题F2|pij(t)=bijt|Fh(∑Cj|Cmax),其中Fh(∑Cj|Cmax)表示在Cmax极小的条件下求∑Cj最小。对这个问题,Cheng等[44]给出了一个混合整数规划模型,并提出了2个启发式算法和分支定界算法。 3.2m台机器情况 赵传立等[23]研究了m台机器的流水作业排序问题Fm|pij(t)=bij(A+Bt)|∑Cj,证明了问题Fm|pij(t)=bij(A+Bt),bij=bj|∑Cj能够在O(nlogn)时间内解决,即把工件按照恶化率bj非增的顺序排列得最优排序。 Cheng等[33]研究了问题Fm|pij(t)=aij+bt,no-idle,β|∑Cj,其中β∈{idm,ddm,idm-ddm,ddm-idm}。他们对机器满足优势关系的特殊情况(即β∈{idm,ddm,idm-ddm,ddm-idm}),分别给出了多项式时间算法。 潘明和赵传立[34]研究了问题Fm|pij(t)=aij+bt,no-idle,β|∑Cj,其中机器满足优势关系β∈{idm-ddm-idm,ddm-idm-ddm}。他们对这两种特殊情况分别给出了多项式时间算法。 Sun等[35]研究了同Cheng等[33]一样的问题(即问题Fm|pij(t)=aij+bt,no-idle,β|∑Cj,其中β∈{idm,ddm,idm-ddm,ddm-idm}),他们用反例说明了Cheng等[33]中的一些结论是不正确的,并给出了修正过的相关结论。 Ng等[36]研究了问题Fm|pij(t)=aij+bt,β|∑Cj,其中β∈{idm,ddm,idm-ddm,ddm-idm,no-wait,no-idle}。他们对一些工件不等待情况、机器无空闲情况和一般(没有工件不等待和机器无空闲限制)情况(即问题Fm|pij(t)=aij+bt,β|∑Cj,其中β∈{idm,ddm,idm-ddm},Fm|pij(t)=aij+bt,no-wait,β|∑Cj,其中β∈{idm,ddm,idm-ddm},和Fm|pij(t)=aij+bt,no-idle,β|∑Cj,其中β∈{idm,ddm,idm-ddm,ddm-idm}),分别给出了多项式时间算法。 Lee等[45]研究了每台机器的恶化率不同的排序问题Fm|pij(t)=aij+bit|∑Cj,他们给出了分支定界算法和多种启发式算法来求解这个问题,并对这些算法进行了比较。 本节主要考虑一些其它的目标函数,包括最大延迟(迟后)时间、加权总完工时间、最大费用、总延误时间。 表2 总完工时间目标函数∑Cj 4.1两台机器情况 Kononov[20]证明了问题F2|pij(t)=bijt|Lmax是强NP-难的。 Yang和Wang[46]研究了具有2台机器的问题F2|pij(t)=bijt|∑wjCj,他们证明了一些特殊情况(包括问题F2|pij(t)=bijt,M1 Bank等[47]研究了具有2台机器的问题F2|pij(t)=bij(A+Bt)|∑Tj,他们给出了分支定界算法,计算结果表明,分支定界算法比较有效。 4.2m台机器情况 赵传立等[23]研究了m台机器的流水作业排序问题Fm|pij(t)=bij(A+Bt)|hmax,证明了问题Fm|pij(t)=bij(A+Bt),bij=bj|hmax能够在O(nlogn)时间内解决。他们还证明了当hmax=Lmax时,最优排序能够通过EDD规则(即时把工件按照工期dj非增的顺序排列)得到。 赵传立等[30]研究了m台机器的流水作业排序问题Fm|pij(t)=bijt,idm|∑wjCj和Fm|pij(t)=bijt,idm|Lmax。他们对这两个问题分别给出了多项式时间算法。 Wang和Xia[31]研究了m台机器的流水作业排序问题Fm|pij(t)=bijt,β|γ,其中β∈{idm,ddm,idm-ddm,ddm-idm},γ∈{Lmax,Tmax,∑wjCj}。他们对一些工件不等待(no-wait)情况、机器无空闲(no-idle)情况和一般(没有工件不等待和机器无空闲限制)情况(即Fm|pij(t)=bijt,β|∑wjCj,其中β∈{ddm,idm-ddm},Fm|pij(t)=bijt,no-wait,β|∑wjCj,其中β∈{idm,ddm,idm-ddm},Fm|pij(t)=bijt,no-idle,β|∑wjCj,其中β∈{idm,ddm,idm-ddm,ddm-idm},Fm|pij(t)=bijt,no-wait,idm|Lmax和Fm|pij(t)=bijt,no-idle,β|Lmax,其中β∈{idm,ddm,idm-ddm,ddm-idm}),分别给出了多项式时间算法。 Wang和Xia[32]研究了与Wang和Xia[31]类似的问题,只是Wang和Xia[32]研究的是成比例恶化函数(即aij-kbij)。 Lee等[48]研究了问题Fm|pij(t)=aij+bit|∑Tj,他们给出了分支定界算法和模拟退化算法、粒子群优化算法两种启发式算法来求解这个问题,并对这些算法进行了比较,比较结果表明:当工件规模较小时,由于两种启发式算法的执行时间都不到一分钟,没有谁更占主导性地位,两种算法都比较适用;对于大规模的工作,模拟退化算法在精确性和执行时间上占有很大的优势。 Bank等[49]研究了问题Fm|pij(t)=bij(A+Bt)|∑Tj,他们给出了粒子群算法和模拟退火算法,计算结果表明,具有局部搜索的粒子群算法优于模拟退火算法。 表3 其他目标函数 具有依赖开工时间恶化工件的流水作业排序问题是一类很有意义的排序问题,相关的研究已经有了一些成果(可参见表1-3)。目标函数主要包括最流行的Cmax和∑Cj,和一些不太流行的∑wjCj,∑Tj,Tmax和Lmax。所用的方法包括复杂性分析、启发式算法、分支定界法、模拟退化算法、粒子群优化算法等。除了本文提到的研究,下面的一些问题仍然没有被解决,值得研究,比如: (1)已有研究的成果都是假定恶化(缩短)函数为简单或特殊的线性函数,然而对于一般线性函数(即pij(t)=aij+bijt)或非线性函数,研究的结果很少。因此,对于一般的线性函数(即pij(t)=aij+bijt)或非线性函数,研究使最大完工时间、(加权)总完工时间极小化问题,这些问题大多数是NP-难的,对这些问题如何设计求解算法,得到一般性结论。 (2)根据上面的研究综述,大多数的研究是单目标问题,对于多目标问题结果却很少(除了文献Cheng等[44])。因此,探讨多目标问题的计算复杂性及求解算法,特别是研究双目标函数的四种组合,即对于目标γ1和γ2,研究λγ1+(1-λ)γ2极小化问题(P1问题);研究在γ1≤Υ(γ2≤K)条件下极小化γ2(γ1)问题(P2(P3)问题);研究(γ1,γ2)的Pareto-最优解集合问题(假如不存在另一个排序π′满足γ1(π′)≤γ1(π)和γ2(π′)≤γ2(π),且其中至少一个不等式严格成立,则排序π是Pareto-最优解,简记为P4问题)。 [1]唐恒永,赵传立.排序引论[M].北京:科学出版社,2002. [2]唐国春,张峰,罗守成,等.现代排序论[M].上海:上海科学普及出版社,2003. [3]PINEDO M L.Scheduling:Theory,Algorithms,and Systems[M].3rd ed.New York:Springer-Verlag New York Inc,2008. [4]GAWIEJNOWICZ S.Time-Dependent Scheduling[M].Berlin:Springer,2008. [5]唐国春.关于Scheduling中文译名的注记[J].系统管理学报,2010,19(6):713-716. [6]唐国春.排序论基本概念综述[J].重庆师范大学学报,2012,29(4):1-11. [7]刘鹏,周晓晔,衣娜.带有减少线性恶化效应的双代理调度问题[J].系统工程学报,2011,26(3):387-392. [8]GUPTA J N D,GUPTA S K.Single facility scheduling with nonlinear processing times[J].Computers and Industrial Engineering,1988,14(4):387-393. [9]BROWNE S,YECHIALI U.Scheduling deteriorating jobs on a single processor[J].Operations Research,1990,38(3):495-498. [10]MOSHEIOV G.Scheduling jobs under simple linear deterioration[J].Computers and Operations Research,1994,21(6):653-659. [11]赵传立,张庆灵,唐恒永.一类线性加工时间单机调度问题[J].自动化学报,2003,29(05):703-708. [12]WANG J B,WANG J J,JI P.Scheduling jobs with chain precedence constraints and deteriorating jobs[J].Journal of the Operational Research Society,2011,62(9):1765-1770. [13]WANG J B,HUANG X,WU Y B,et al.Group scheduling with independent setup times,ready times,and deteriorating job processing times[J].International Journal of Advanced Manufacturing Technology,2011,60(5-8):643-649. [14]王吉波,刘璐,许扬涛,等.具有恶化工件的不同工期指派问题研究[J].沈阳航空航天大学学报,2013,30(5):83-87. [15]FRAMINAN J,GUPTA J,LEISTEN R.A review and classification of heuristics for permutation flow-shop scheduling with makespan objective[J].Journal of the Operational Research Society,2004,55(12):1243-1255. [16]RUIZ R,MAROTO C.A comprehensive review and evaluation of permutation flowshop heuristics[J].European Journal of Operational Research,2005,165(2):479-494. [17]EMMONS H,VAIRAKARAKIS G.Flow shop scheduling-theoretical results,algorithms and applications[M].Berlin:Springer,2013. [18]FERNANDEZ-VIAGAS V,FRAMINAN J M.NEH-based heuristics for the permutation flowshop scheduling problem to minimise total tardiness[J].Computers & Operations Research,2015,60(C):27-36. [19]KONONOV A,GAWIEJNOWICZ S.NP-hard cases in scheduling deteriorating jobs on dedicated machines[J].Journal of the Operational Research Society,2001,52(6):708-717. [20]KONONOV A.Combinatorial complexity of scheduling jobs with simple linear deterioration[J].Discrete Analysis and Operations Research,1996,3(2):15-32. [21]MOSHEIOV G.Complexity analysis of job-shop scheduling with deteriorating jobs[J].Discrete Applied Mathematics,2002,117(1-3):195-209. [22]JOHNSON S M.Optimal two and three stage production schedules with setup times included[J].Naval Research Logistics Quarterly,1954,1(1):61-68. [23]赵传立,张庆灵,唐恒永.具有线性恶化加工时间的调度问题[J].自动化学报,2003,29(04):531-535. [24]LEE W C,WU C C,WEN C C,et al.A two-machine flowshop makespan scheduling problem with deteriorating jobs[J].Computers & Industrial Engineering,2008,54(4):737-749. [25]ZHAO C,TANG H.Two-machine flow shop scheduling with deteriorating jobs and chain precedence constraints[J].International Journal of Production Economics,2012,136(1):131-136. [26]WANG L,SUN L Y,SUN L H,et al.On three-machine flow shop scheduling with deteriorating jobs[J].International Journal of Production Economics,2010,125(1):185-189. [27]WANG J B,WANG M Z.Minimizing makespan in three-machine flow shops with deteriorating jobs[J].Computers & Operations Research,2013,40(2):547-557. [28]WANG J B,WANG M Z.Makespan minimization on three-machine flow shop with deteriorating jobs[J].Asia-Pacific Journal of Operational Research,2013,30(6):1350022-1-1350022-14. [29]MELNIKOV O I,SHAFRANSKY Y M.Parametric problem in scheduling theory[J].Cybernetics,1979,15(3):352-357. [30]赵传立,张庆灵,唐恒永.加工时间依赖开工时间的Flow Shop调度问题[J].系统工程与电子技术,2003,25(3):292-294. [31]WANG J B,XIA Z Q.Flow shop scheduling with deteriorating jobs under dominating machines[J].Omega,2006,34(4):327-336. [32]WANG J B,XIA Z Q.Flow shop scheduling problems with deteriorating jobs under dominating machines[J].Journal of the Operational Research Society,2006,57(2):220-226+7. [33]CHENG M,SUN S,HE L.Flow shop scheduling problems with deteriorating jobs on no-idle dominant machines[J].European Journal of Operational Research,2007,183(1):115-124. [34]潘明,赵传立.具有优势机器和恶化工件的流水作业排序问题[J].系统管理学报,2008,17(6):686-692. [35]SUN L H,SUN L Y,CUI K,et al.A note on flow shop scheduling problems with deteriorating jobs on no-idle dominant machines[J].European Journal of Operational Research,2010,200(1):309-311. [36]NG C T,WANG J B,CHENG T C E,et al.Flowshop scheduling of deteriorating jobs on dominating machines[J].Computers & Industrial Engineering,2011,61(3):647-654. [37]SUN L H,SUN L Y,WANG M Z,et al.Flow shop makespan minimization scheduling with deteriorating jobs under dominating machines[J].International Journal of Production Economics,2012,138(1):195-200. [38]WANG J B.Flow shop scheduling with deteriorating jobs under dominating machines to minimize makespan[J].International Journal of Advanced Manufacturing Technology,2010,48(5):719-723. [39]YIN N,KANG L.Minimizing makespan in permutation flow shop scheduling with proportional deterioration[J].Asia-Pacific Journal of Operational Research,2015,32(6):1550050-01-1550050-12. [40]WANG J B,NG C T,CHENG T C E,et al.Minimizing total completion time in a two-machine flow shop with deteriorating jobs[J].Applied Mathematics and Computation,2006,180(1):185-193. [41]SHIAU Y R,LEE W C,WU C C,et al.Two-machine flowshop scheduling to minimize mean flow time under simple linear deterioration[J].International Journal of Advanced Manufacturing Technology,2007(34):774-782. [42]WU C C,LEE W C.Two-machine flowshop scheduling to minimize mean flow time under linear deterioration[J].International Journal of Production Economics,2006,103(2):572-584. [43]NG C T,WANG J B,CHENG T C E,et al.A branch-and-bound algorithm for solving a two-machine flow shop problem with deteriorating jobs[J].Computers and Operations Research,2010,37(1):83-90. [44]CHENG M,TADIKAMALLA P R,SHANG J,et al.Bicriteria hierarchical optimization of two-machine flow shop scheduling problem with time-dependent deteriorating jobs[J].European Journal of Operational Research,2014,234(3):650-657. [45]LEE W C,WU C C,CHUNG Y H,et al.Minimizing the total completion time in permutation flow shop with machine-dependent job deterioration rates[J].Computers and Operations Research,2009,36(6):2111-2121. [46]YANG S H,WANG J B.Minimizing total weighted completion time in a two-machine flow shop scheduling under simple linear deterioration[J].Applied Mathematics and Computation,2011,217(9):4819-4826. [47]BANK M,FATEMI GHOMI SMT,JOLAI F,et al.Two-machine flow shop total tardiness scheduling problem with deteriorating jobs[J].Applied Mathematical Modelling,2012,36(11):5418-5426. [48]LEE W C,YEH W C,CHUNG Y H.Total tardiness minimization in permutation flowshop with deterioration consideration[J].Applied Mathematical Modelling,2014(38):3081-3092. [49]BANK M,FATEMI GHOMI SMT,JOLAI F,et al.Application of particle swarm optimization and simulated annealing algorithms in flow shop scheduling problem under linear deterioration[J].Advances in Engineering Software,2012,47(1):1-6. (责任编辑:陈素清英文审校:刘勇进) Survey on flow shop scheduling problems with start time dependent deteriorating jobs WANG Ji-bo1,2,GUO Miao-miao1,LIU Huan3,LI Lin2,WANG Dan4 (1.College of Economics and Management,Shenyang Aerospace University,Shenyang 110136,China;2.College of Science,Shenyang Aerospace University,Shenyang 110136,China;3.Department of Educational Administration,Liaoning Sports School,Shenyang 110179,China;4.College of Computer Science,Shenyang Aerospace University,Shenyang 110136,China) Scheduling with deteriorating jobs is important in manufacturing,operations research,and management science and engineering,and it is widely used in such fields as iron and steel,plastic,military and medical industries.This paper introduced the characteristics of the flow shop scheduling with start-time dependent deteriorating jobs whose objectives functions mainly included the make-span,total completion time,total weighted completion time,maximum lateness and total tardiness.Then it gived an overall survey on the scheduling,and points out the existing drawback and many problems to be solved.Finally,further relative researches were suggested. scheduling;flow shop;deteriorating job 2095-1248(2016)03-0001-10 2016-04-11 国家自然科学基金(项目编号:61403260;71471120) 王吉波(1975-),男,辽宁沈阳人,教授,博士后,博士生导师,主要研究方向:生产计划与排序,E-mail:wangjibo75@163.com。 O223;C934 A 10.3969/j.issn.2095-1248.2016.03.0012 最小化时间表长目标函数
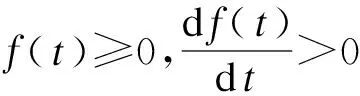

3 最小化总完工时间目标函数
4 极小化其它目标函数


5 结论及展望


