钛内衬复合材料环形气瓶结构设计与优化

祖　磊，汪　洋，王继辉，李书欣，王　路，谢丽婷

(武汉理工大学 材料科学与工程学院，武汉 430070)



钛内衬复合材料环形气瓶结构设计与优化

祖磊，汪洋，王继辉，李书欣，王路，谢丽婷

(武汉理工大学 材料科学与工程学院，武汉 430070)

根据微分几何，推导环形气瓶测地线缠绕轨迹以及缠绕角应满足的稳定缠绕条件，并针对不同切点数进行线型轨迹仿真。基于有限元分析，针对钛合金内衬环形气瓶的初始缠绕角及缠绕层数进行优化设计，并评估对比有、无环向补强层的环形气瓶承载能力。结果表明：本文设计的测地线轨迹精确可靠，很好地满足环形气瓶的缠绕工艺性。优化设计的缠绕参数既满足工艺可缠性，又能提高环形气瓶的结构性能。此外，有环向补强层的气瓶爆破强度提高了14%，钛合金内衬屈服强度提高了24.8%。因此，采用环向补强层有利于进一步提高环形气瓶的承载性能。水压实验结果表明本文设计方法预测的变形和爆破压力与实验值吻合良好。

复合材料；纤维缠绕；环形气瓶；测地线；结构设计

随着先进树脂基复合材料的不断发展以及成型技术的提高，其应用范围越来越广阔。成熟的技术也使得复合材料由最初仅用于制造装饰件而逐步发展为用于制造安全系数和质量要求更高的结构件。发展至今先进复合材料更是已广泛应用于要求严格的航空航天以及军事领域[1-4]。

纤维缠绕技术是复合材料压力容器的主要成型加工方法，由于其制品具有比强度高、比模量大、可设计性好、质量稳定、自动化生产效率高等显著优点，已广泛应用于国防及民用工业中，如固体火箭发动机壳体、高压气瓶、油气管道、储罐、汽车及船舶工业等[5-9]。近年来，复合材料环形气瓶在天然气汽车、导弹、飞行器、潜艇中逐步得到发展和日益广泛的应用。由于其特殊的双向弯曲闭合曲面形状，可有效避免筒形气瓶封头部位的应力集中与纤维厚度严重堆积等现象，且可充分利用和节省空间，因此在减轻储能系统质量、消除质心漂移等方面具有较大优势[10-15]。

自1943年Courant首次提出有限元的思想以来，随着有限元理论的不断完善以及计算机技术的发展，有限元法(Finite Element Method, FEM)飞速发展。最初FEM仅用于解决平面结构问题，发展至今，已扩展到电磁学、热学、光学、生物医学等方面问题[16-20]。材料库也由最初的弹性材料发展为弹塑性、塑性、黏弹性、弹塑性以及复合材料。使用领域涉及航空航天、土木建筑、机械制造、船舶、电子技术等。

本工作根据微分几何和圆环面参数方程，推导环形气瓶缠绕的测地线轨迹方程，并计算相应于不同切点数的缠绕线型。同时采用有限元软件ANSYS12.0，针对钛合金内衬复合材料环形气瓶的初始缠绕角度及铺层数进行优化设计。另外，在最佳初始缠绕角的基础上分析采用环向补强层对环形气瓶承载性能的影响。相比于传统设计方法，本工作提出的方法可有效降低复合材料环形气瓶的设计成本与缩短设计周期，并大幅提高环形气瓶的结构性能与承载能力。

1　环形气瓶线型设计

环形容器的回转曲面是由一个半径为r的母圆上每一点绕这个圆所在平面内的某一轴(与这个圆的圆心距离为R)回转而成的，如图1所示。本文分析的环形容器R=260mm，r=65mm。母圆上的任意一点回转而成的圆周线称为纬圆(或平行圆)。纬圆上的一段弧线称为纬线，纬线对应的圆周角为θ角。母圆在回转时的任一位置的圆周线称为经线或子午线(对应的圆周角为φ角)。环形容器的参数曲面方程由下式给出：

(1)

式中：r为管半径；R为圆环面中心线曲率半径；θ为张角；φ为母圆线型转角。

图1　圆环面及其纤维轨迹示意图Fig.1　Schematic diagram of torus and its fiber paths

从数学的拓扑结构来看，圆环面是十分简单的曲面，但从稳定缠绕的角度来看，由于其非轴对称性，可称为复杂曲面。设α为缠绕角，在数学上α为纤维曲线正向与θ参数曲线所成的锐角。

根据微分几何[21]，曲面上的Liouville公式为：

(2)

其中E,G为曲面第一基本形式的系数，针对圆环面由式(1)可得：

(3)

将式(3)代入式(2)可计算出圆环面曲线的测地曲率kg见式(2):

(4)

其中s为曲线弧长。根据测地线的定义，令kg=0，可得圆环面上的测地线方程，见式(5)：

(5)

由曲面几何参数之间关系[11]以及式(5)可得出式(6),(7)：

(6)

(7)

对(6)式积分可得Clairaut公式在圆环面上的推广公式，见式(8)：

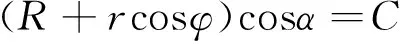
(8)

其中C为常数，由初始缠绕起点的位置和切矢决定。通过四阶Runge-Kutta方法可做出一个周期内环形气瓶测地线缠绕轨迹的三维仿真图形，如图2所示。此外对应于4～7切点缠绕线型(初始缠绕角α0=60°～69°)的仿真结果如图3所示。

由于圆环面是非凸曲面，采用测地线缠绕圆环内侧凹面时有可能产生架空现象。为了防止出现该类情况，初始缠绕角α0必须满足式(7)[14]。计算可知本文分析的环形容器初始缠绕角不得小于59°。另外考虑气瓶的结构特征，超过70°的缠绕角也难以保证环形气瓶的纬向强度。因此，初始缠绕角范围可选取为(60°～70°)。

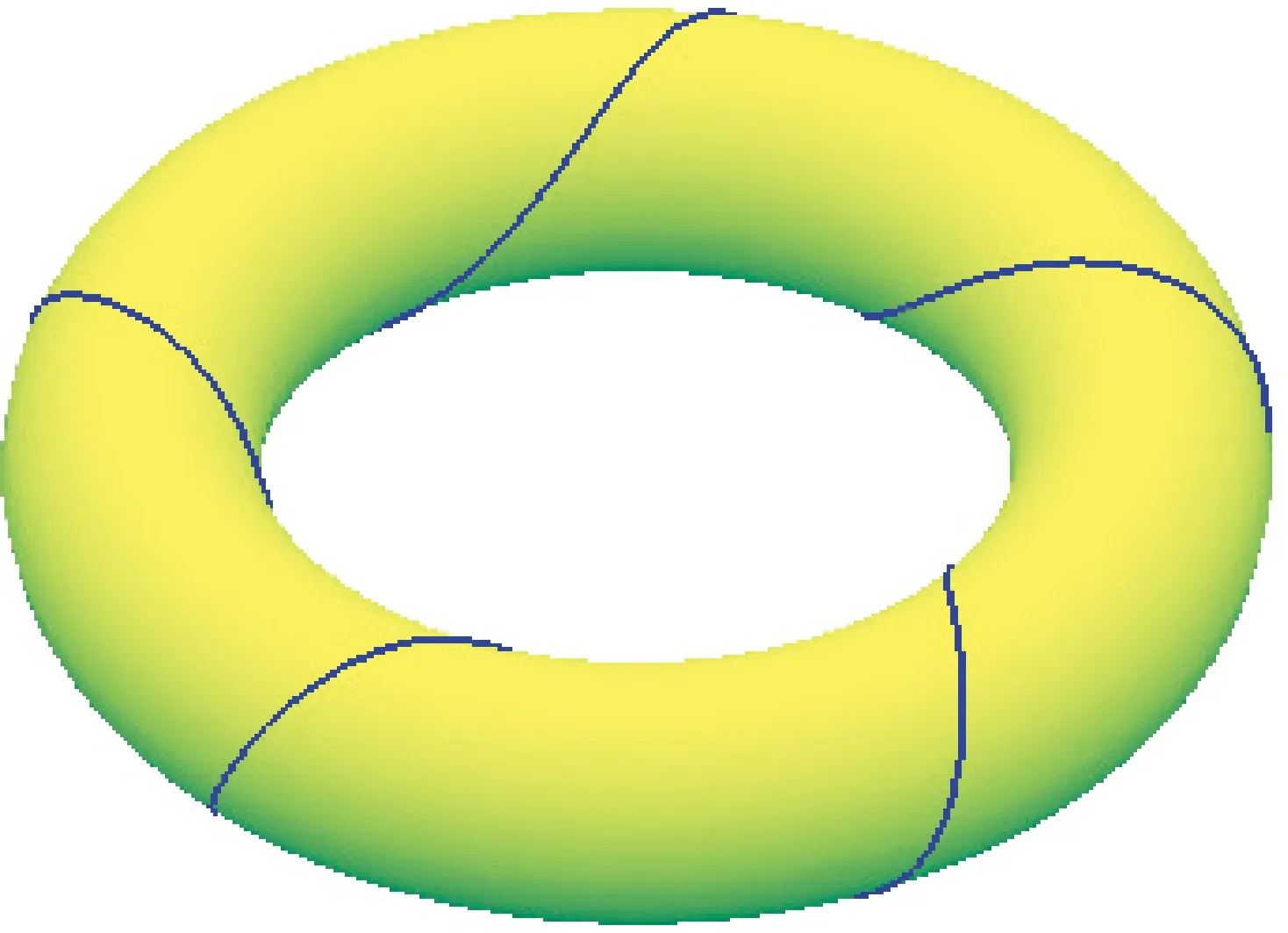
图2　圆环面上一个周期的测地线缠绕轨迹Fig.2　Geodesic trajectories of a complete wound circuit

(9)

2　有限元模型

气瓶结构主要包含两个部分：内衬和纤维增强层。由于环形气瓶特有的几何形状以及缠绕工艺的特点，气瓶纤维层厚度并不是均匀的，而是从气瓶外侧到内侧逐渐增加。并且纤维缠绕角也是限有着母圆线型转角φ变化而变化。因此选用ANSYS12.0中的壳单元Shell91建立全模型，如图4。该单元具有较好的非线性特性，并可通过赋予实参数的手段实现结构的变厚度、变缠绕角以及不同材料层问题。钛合金内衬采用双线性随动强化模型(BKIN)模拟其塑性变形。在气瓶最外层的四等分点上进行约束。整个模型由3840个单元组成。分析所用材料参数见表1，材料破坏强度见表2。

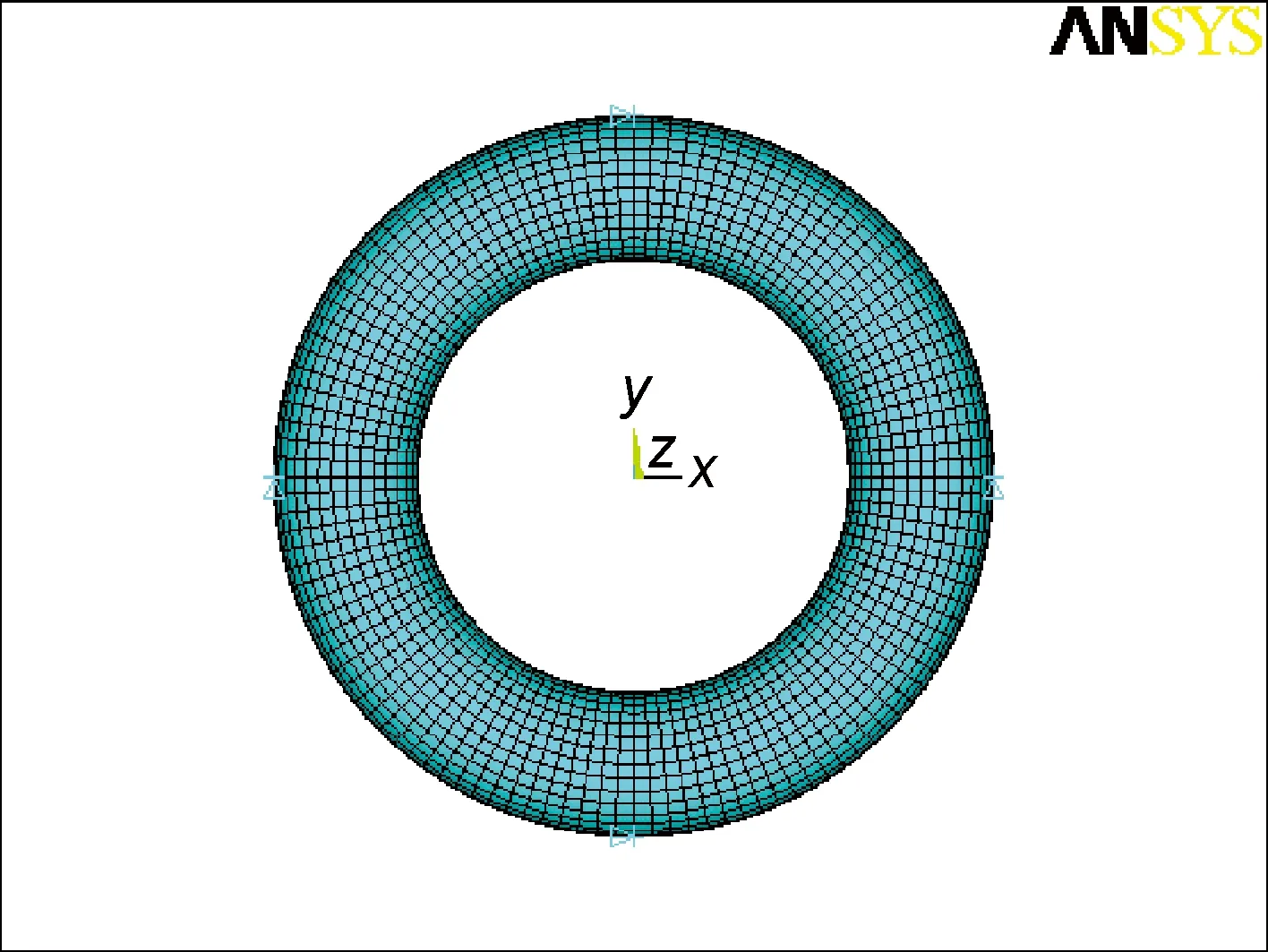
图4　气瓶有限元模型Fig.4　The FEM model of a toroidal pressure vessel

3　模拟结果与分析

3.1起始缠绕角及厚度优化结果

由前所述，根据缠绕工艺性和气瓶的结构特征，初始缠绕角优化设计的区间范围为60°～70°。根据工艺要求，缠绕单层厚度0.18mm，采用±α交替缠绕。而气瓶总质量不得高于12kg，缠绕层质量≤4.1kg。因而复合材料层数不超过16层。值得注意的是钛合金内衬厚度相对于缠绕单层厚度过大，分析时由于Shell单元的特性，需将钛合金层分为等厚度的5层。

表1　材料参数

表2　材料强度

考虑实际加工精度，分别模拟80MPa内压下初始缠绕角α为60°，62°，64°，66°，68°以及70°时不同层数下的气瓶失效情况。出于保守设计选择蔡-吴准则进行失效判断。模拟结果见表3。从表3中可知，初始缠绕角为60°和70°时，纤维层需达到12层才可以满足气瓶力学要求，相比于其他角度，无法满足质量最优。初始缠绕角为62°，64°，66°以及68°时虽然纤维层数均为10层时就可满足条件。但其实缠绕角为64°时具有最小变形。故而最佳的缠绕角为64°，最佳缠绕层数为10层。此角度正好对应5切点线型。但实际情况下考虑各种误差，最佳缠绕层应取12层。

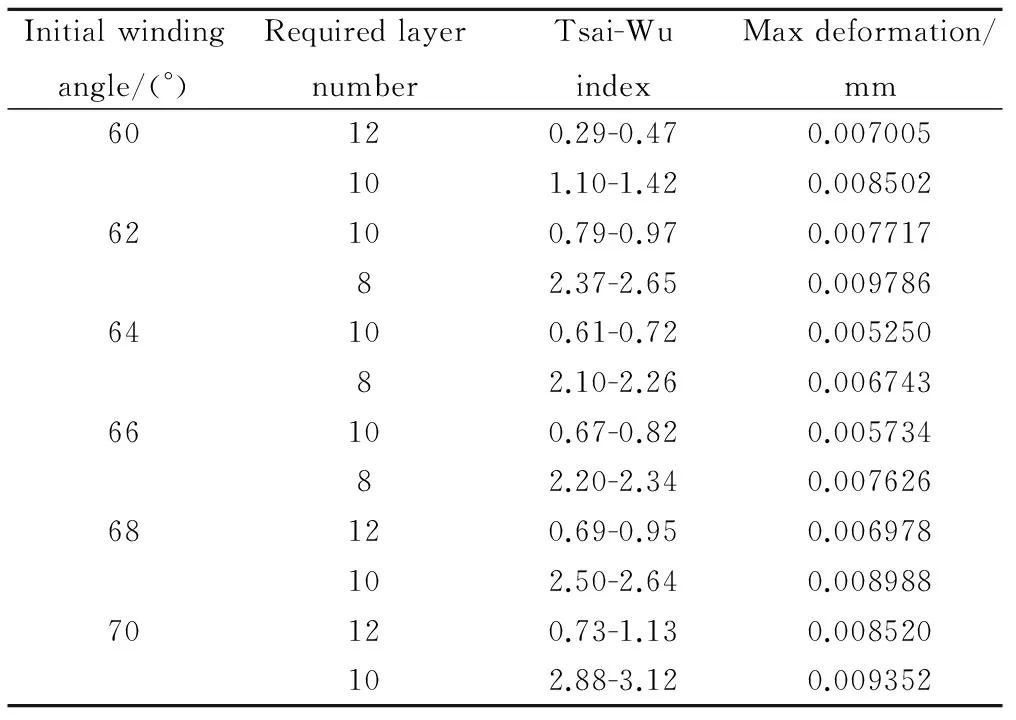
表3　气瓶缠绕角(60°～70°)及层数优化结果

3.2小环向补强层对气瓶影响

起始缠绕角64°不变，选取两种铺层方式进行模拟：方案1，±α交替缠绕12层；方案2，在方案1的基础上添加小环向补强层。由于钛合金内衬具有较好的密封性，故以纤维的破坏作为气瓶的最终失效形式。

按方案1的铺层方式制作的气瓶爆破压力为86MPa。纤维缠绕层应力情况见图5，钛合金内衬等效应力分布见图8。此外模拟了内压为30，37.5，60MPa时的气瓶受力情况，结果如表4所示。相同压力下的采用方案2铺层制作的气瓶受力情况如表5所示。

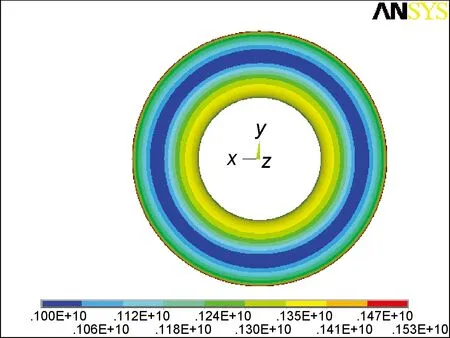
图5　纤维方向应力SxFig.5　Longitudinal stress Sx of the composite overwrap

对比表4和表5可知，两种铺层方案气瓶在低内压条件下，应力水平以及变形量差别不大。但当内压进一步提升后，两者的应力水平明显增大：补强后的气瓶破坏强度提高14%。60MPa内压条件下，补强后气瓶变形量减小52%。进一步模拟分析可知，按方案1铺层制得的气瓶在内压到达38.3MPa时，钛合金内衬的内侧将开始发生塑性变形，受力情况见图9(a)；按方案2制得的气瓶当内压到达47.8MPa时，钛合金内衬的内侧将开始发生塑性变形，此时受力情况如图9(b)所示。补强气瓶钛内衬临界屈服内压提高24.8%。

表4　第一种铺层方式气瓶FEM分析结果

表5　第二种铺层方式气瓶分析结果

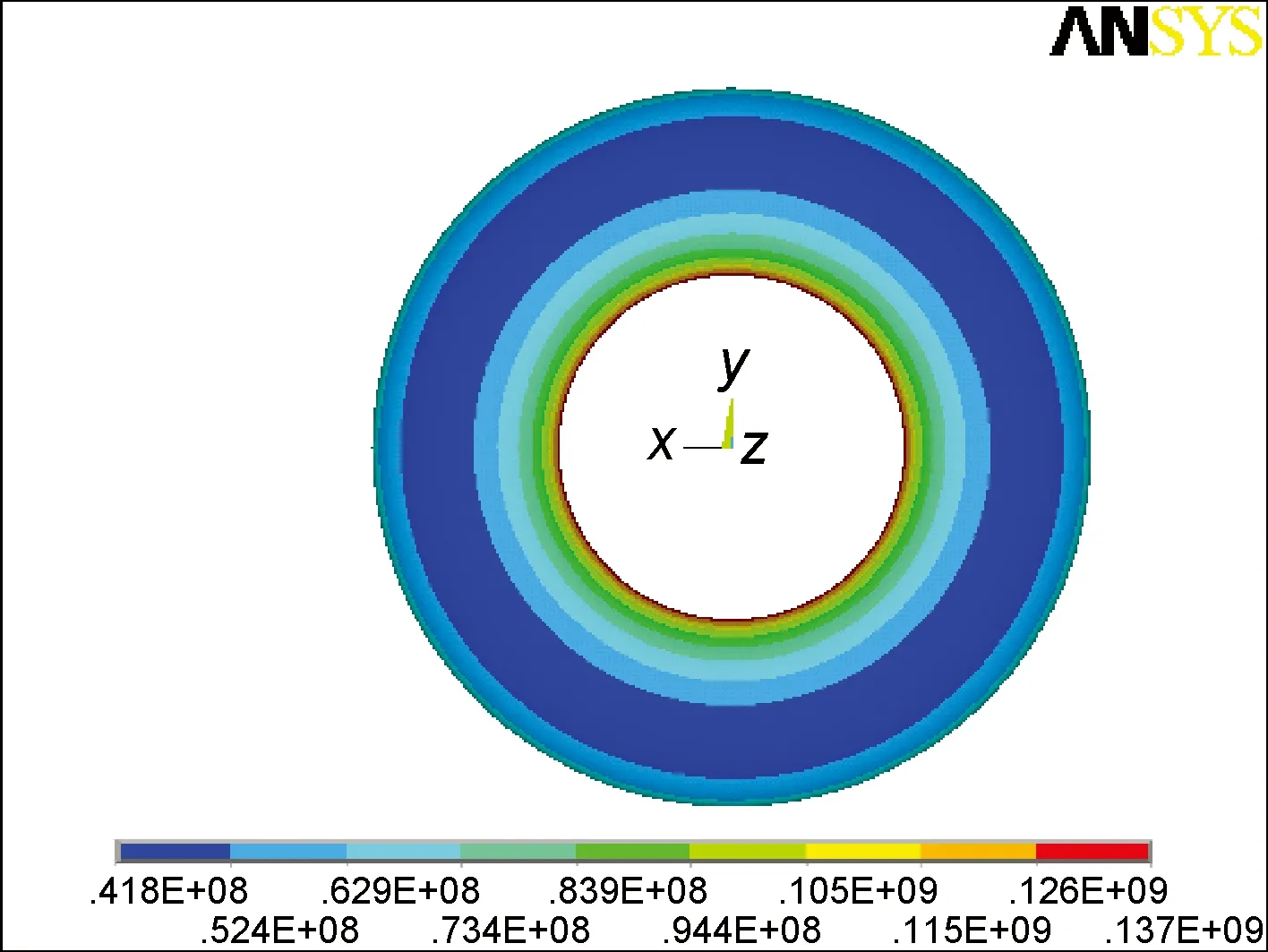
图6　垂直于纤维方向应力SyFig.6　Transverse stress Sy of the composite overwrap

4　环形气瓶水压实验

为验证该设计方法的可行性，采用第二种铺层方式制作了钛内衬复合材料环形气瓶，并通过水压实验测试了不同水压下的变形以及爆破压力。其测试装置如图10所示，分别在A，B两个方向测试了最大变形值，如表6所示。

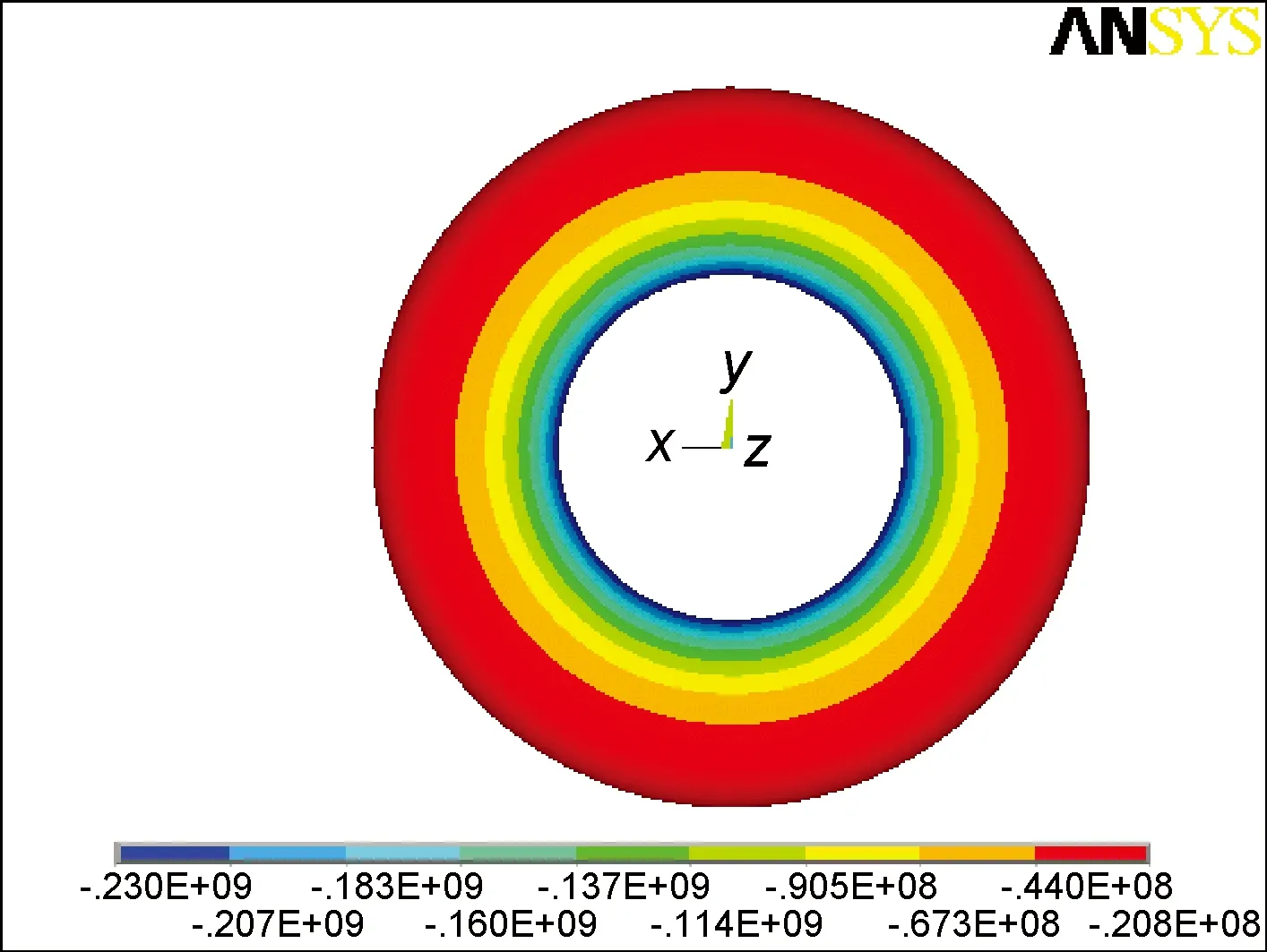
图7　面内剪切应力SxyFig.7　In-plane shearing stress Sxy of the composite overwrap

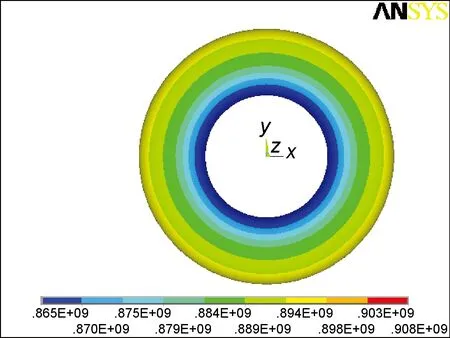
图8　钛内衬等效应力Fig.8　Equivalent stress of the titanium liner

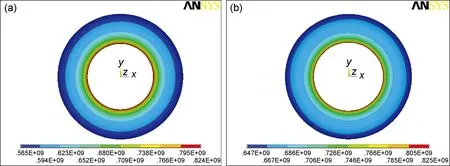
图9　两种铺层方式气瓶内衬临界屈服点应力分布(a)未补强气瓶内衬临界屈服点的等效应力分布;(b)补强气瓶内衬临界屈服点的等效应力分布Fig.9　Equivalent stress of the titanium liner at the yield point(a)without hoop reinforcement under P=38.3MPa;(b)with hoop reinforcement under P=47.8MPa

图10　水压实验装置示意图Fig.10　Schematic of hydrostatic test instrument

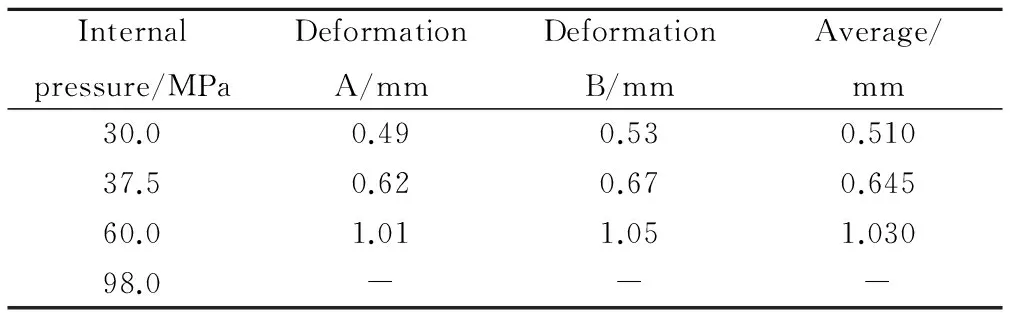
Internalpressure/MPaDeformationA/mmDeformationB/mmAverage/mm30.00.490.530.51037.50.620.670.64560.01.011.051.03098.0---

从表中数据分析可知，环形气瓶的变形值随压力的增大而增加，在测试的两个方向测试值略有不同，这可能是由测试误差造成的。测试所得变形值与表5所示的有限元模型预测值基本吻合，最大偏差不超过10%。经水压爆破实验测试的爆压为90MPa，略低于理论预测值98MPa，考虑到复合材料制造工艺的离散性和测试的实验误差，该结果与数值分析结果基本吻合良好。因此，水压实验证明本文所提出的设计方法是可行的。

5　结论

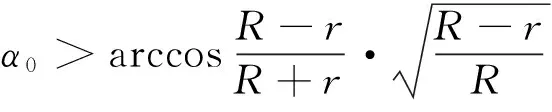
(2)以Tsai-Wu准则作为失效判据和约束准则，环形气瓶的质量和变形量作为优化目标，利用有限元方法优化计算得出环形气瓶最佳纤维缠绕角为64°，所对应的缠绕层数为10层。此角度正好对应五切点缠绕线型。另外，实际生产时应考虑由于计算误差和工艺缺陷引起的折减安全系数，因此缠绕层取12层为宜。

(3)按方案1(无环向补强层)设计的气瓶爆破压力为86MPa。钛合金内衬临界屈服内压为38.3MPa；按方案2(有环向补强层)设计的气瓶爆破压力为98MPa。钛合金内衬临界屈服内压为47.8MPa。由此可见，环向补强后的环形气瓶爆破强度提高了14%，钛合金内衬临界屈服内压提高了24.8%。此外，60MPa内压下，环向补强后气瓶变形量减小了52%。因此，采用合适的环向补强能进一步提高复合材料环形气瓶的结构承载能力。水压实验测试数据表明本文设计方法得到的变形和爆破压力与实验结果吻合良好。

[1]张靠民，李敏，顾轶卓,等. 汽车用先进复合材料的低成本技术[J].玻璃钢/复合材料，2012,(增刊1): 226-231.

ZHANG Kao-min, LI Min, GU Yi-zhuo, et al. Advanced composite materials and key technology for automotive [J]. Fiber Reinforced Plastics/Composites, 2012, (Suppl 1): 226-231.

[2]罗刚堂，李敏，顾轶卓,等. 共胶接T型加筋壁板模具设计及成型工艺研究[J].玻璃钢/复合材料，2012，(5): 58-64.

LUO Gang-tang, LI Min, GU Yi-zhuo, et al. Study on design of mould assembly and molding processing for co-bonding T-stiffened skin structure [J]. Fiber Reinforced Plastics/Composites, 2012, (5):58-64.

[3]何楠，杨加斌，高峰．先进复合材料在军用无人机上的应用动向[J]．玻璃钢/复合材料，2013, (2):94-97.

HE Nan, YANG Jia-bin, GAO Feng. Application tendency of advanced composite materials for military unmanned aerial vehicles [J]. Fiber Reinforced Plastics/Composites, 2013, (2):94-97.

[4]方宜武，王显峰，孙成,等．复合材料机翼翼梁的制造及应用概况[J]．玻璃钢/复合材料，2014，(2): 69-74.

FANG Yi-wu, WANG Xian-feng, SUN Cheng, et al. The manufacture and application of composite wing spars [J]. Fiber Reinforced Plastics/Composites, 2014, (2): 69-74.

[5]WANG R, YANG F, LIU W, et al. Research on stability condition of polar winding on the dished head [J]. Polym Polym Composites, 2011, 19(4-5): 339-344.

[6]WANG R, JIAO W, YANG F. A new method for predicting dome thickness of composite pressure vessels [J]. J Reinf Plast Composites, 2010, 29(22): 3345-3352.

[7]矫维成，王荣国，刘文博,等. 纤维缠绕复合材料压力容器封头厚度预测[J]．复合材料学报，2010, 27(5): 116-121.

JIAO Wei-cheng, WANG Rong-guo, LIU Wen-bo, et al. Dome thickness prediction of composite pressure vessels [J]. Acta Materiae Compositae Sinica, 2010, 27(5): 116-121.

[8]WANG R, JIAO W, LIU W, et al. Slippage coefficient measurement for non-geodesic filament- winding process [J]. Compos Part A: Appl Sci Manuf,2011, 42(3): 303-309.

[9]矫维成，王荣国，刘文博,等. 缠绕纤维与芯模表面间滑线系数的测量表征[J]．复合材料学报，2012, 29(3): 191-196.

JIAO Wei-cheng, WANG Rong-guo, LIU Wen-bo, et al. Measure of slippage coefficient between fiber and mandrel surface for non-geodesic filament winding [J]. Acta Materiae Compositae Sinica, 2012, 29(3): 191-196.

[10]ZU L, SOTIRIS K, ADRIAAN B. A novel design solution for improving the performance of composite toroidal hydrogen storage tanks [J].International Journal of Hydrogen Energy, 2012, 37(19): 14343-14350.

[11]ZU L, SOTIRIS K, ADRIAAN B. Design of filament-wound circular toroidal hydrogen storage vessels based on non-geodesic fiber trajectories [J]. International Journal of Hydrogen Energy, 2012, 35(2): 660-670.

[12]ZU L, SOTIRIS K, ADRIAAN B. Optimal cross sections of filament-wound toroidal hydrogen storage vessels based on continuum lamination theory [J]. International Journal of Hydrogen Energy, 2012, 35(19): 10419-10429.

[13]LEI Z U, ZHANG D H, XU Y Q, et al. Integral design and simulation of composite toroidal hydrogen storage tanks [J]. International Journal of Hydrogen Energy,2012, 37(1): 1027-1036.

[14]ZU L. Stability of fiber trajectories for winding toroidal pressure vessels[J]. Composite Structures, 2012,94(5): 1855-1860.

[15]ZU L, SOTIRIS K, ADRIAAN B. Minimum weight design of helically and hoop wound toroidal hydrogen storage tanks with variable slippage coefficients [J]. Polymer Composites, 2012, 33(12): 2218-2227.

[16]任铮钺，王立久，孙治国．建筑模网混凝土墙体抗震试验研究与有限元分析[J]. 工程力学，2012,(12): 147-155.

REN Zheng-yue, WANG Li-jiu, SUN Zhi-guo. Experimental research and finite element analysis on seismic behavior of concrete walls with construction formwork [J]. Engineering Mechanics, 2012, (12): 147-155.

[17]廖云祥．冶金机械设计中有限元分析技术的应用[J]．企业技术开发，2013，(9): 88-89.

LIAO Yun-xiang. Application of metallurgical mechanical design based on finite element analysis technology [J]. Technology Development of Enterprise, 2013, (9): 88-89.

[18]杨文芳，魏强，朱兰琴．基于有限元分析的机载电子设备减振设计[J]．振动与冲击，2010, (5): 230-253.

YANG Wen-fang, WEI Qiang, ZHU Lan-qin. Anti-vibration design for an airborne electronic equipment based on finite element method [J]. Journal of Vibration and Shock, 2010, (5): 230-253.

[19]苏春涛，眭承志．腰椎三维有限元生物力学分析的技术应用进展[J]. 中国康复医学杂志，2013，(5): 479-482.

SU Chun-tao, GUI Cheng-zhi. Technical progress in application of three dimensional finite element analysis of biomechanics of lumbar spine [J].Chinese Journal of Rehabilitation Medicine, 2013, (5): 479-482.

[20]赵艳，沈中华，陆建,等．激光在管道中激发周向导波的有限元模拟[J]. 物理学报，2007, 56(1): 321-326.

ZHAO Yan, SHEN Zhong-hua, LU Jian, et al. Finite element simulation of laser-generated circumferential waves in hollow cylinder [J]. Acta Physica Sinca, 2007, 56(1): 321-326.

[21]梅向明，黄敬之. 微分几何[M].4版. 北京: 高等教育出版社，2008. 146-149.

MEI Xiang-ming, HUANG Jing-zhi. Differential Geometry[M]. 4th ed. Beijing: China Higher Education Press, 2008. 146-149.

Structural Design and Optimization of Titanium-lined Composite Toroidal Pressure Vessels

ZU Lei,WANG Yang,WANG Ji-hui,LI Shu-xin,WANG Lu,XIE Li-ting

(School of Materials Science and Engineering,Wuhan University of Technology,Wuhan 430070,China)

The fiber trajectories for geodesically over wound toroidal pressure vessels and related stable winding conditions were derived based on differential geometry. The obtained winding trajectories were also simulated for several conventionally-used partitions. The optimal initial winding angle and minimally required total layer number were determined for titanium-lined filament wound toroidal pressure vessels. The load-carrying capacities of torodal pressure vessels with and without hoop reinforcing layers were respectively calculated and compared to each other. The results show that the designed geodesic patterns are accurate and reliable, and satisfy the windability of toroids. The obtained optimal winding parameters simultaneously meet the windability and improve the vessel performance, and thus the fiber strength can be fully utilized. The results also indicate that the addition of hoop reinforcing layers leads to 14% raise in the burst pressure of the toroidal vessel and 24.8% increase in the yield strength of the titanium liner. Therefore, the load-carrying capacities can be significantly improved by adding hoop reinforcement. The hydrostatic test results show that the deformation and the burst pressure predicted using the present method & model agree well with the experimental data.

composite material；filament winding；toroidal pressure vessel；geodesic；structural design

10.11868/j.issn.1001-4381.2016.02.009

TB332

A

1001-4381(2016)02-0056-07

国家自然科学基金(11302168)；湖北省自然科学基金(2014CFB140)；陕西省自然科学基础研究计划资助项目(2013JQ6018)；中央高校基本科研业务费专项资金资助项目(143101001)

2014-08-25;

2015-04-10

王继辉(1962—)，男，博士，教授，主要从事树脂基复合材料方面的研究，联系地址：湖北省武汉市珞狮路122号武汉理工大学(430070)，E-mail: jhwang@whut.edu.cn