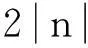一种椭圆曲线消息恢复数字签名方案的分析与改进

周克元

(宿迁学院二系，江苏宿迁　223800)



一种椭圆曲线消息恢复数字签名方案的分析与改进

周克元

(宿迁学院二系，江苏宿迁223800)

对Zhang等提出的椭圆曲线消息恢复数字签名方案进行了分析,指出其验证方程存在错误,且方案无前向安全性,同时任意第三方可恢复消息.给出了一种改进方案,证明了改进方案具有抗伪造签名攻击、前向安全性、公开验证性和指定接收者消息恢复等性质，并对复杂度进行了分析.

椭圆曲线;数字签名;消息恢复;前向安全;消息替换攻击

Diffie等[1]于1976年提出数字签名后,数字签名得到了很大的发展和广泛的应用,各类数字签名方案相继被提出.椭圆曲线签名算法相对于离散对数签名算法拥有更高的安全性,对于基于身份的椭圆曲线数字签名方案,为进一步提高安全性,有的签名方案在使用双密钥的同时又使用了双参数设计签名方案.Zhang等[2]给出了一种基于椭圆曲线的消息恢复数字签名方案,但该方案存在错误,且可被攻击,文中指出了方案的错误并给出一个改进方案.

1　Zhang方案

1.1参数设置

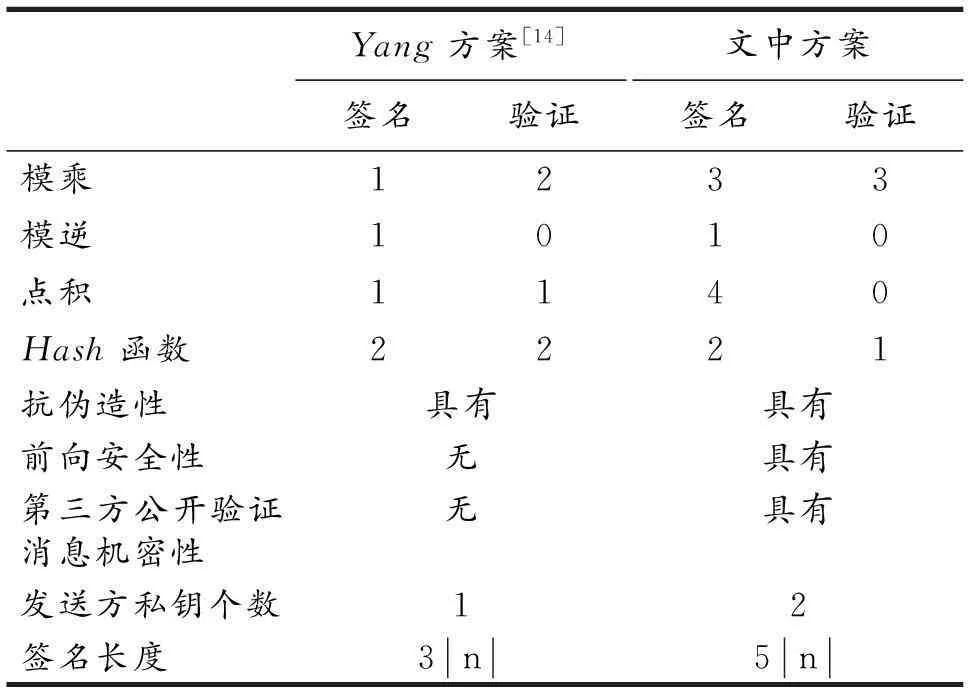
设椭圆曲线参数D=(q,FR,a,b,G,n,h),其中,q为某个素数幂;FR指出Fq中元素的表示方法;a,b∈Fq为椭圆曲线系数;G为椭圆曲线的基点;n为点G的阶,即nG=0，要求n为素数;h为n关于#E(Fq)(椭圆曲线的阶)的协因子,即h=#E(Fq)/n.用户A选取私钥cA1,cA2∈{1,2,…,n-1},且cA1≠cA2,公钥DA1=cA1P,DA2=cA2P.用户B选取私钥cB∈{1,2,…,n-1},公钥DB=cBP.待签名消息为m(m

1.2签名过程

1)用户A任取k1,k2∈{1,2,…,n-1}；

2)计算R=(x1,y1)=(k1+k2)DB, r=mh-1(x1)modn;

3)计算s1=(k1+rcA1)modn, s2=(k2+rcA2)modn.

消息m的签名为(r,s1,s2).

1.3消息恢复及验证

1)接收者B下载发送者A的公钥DA1,DA2；

2)检查r,s1,s2是否属于{1,2,…,n-1},错误则拒绝签名；

3)计算X=(x2,y2)=s1P+s2P-rDA1-rDA2,m′=rh(cBx2) modn；

4)若X=0，则签名错误；否则，B恢复出消息明文m并检查附在m后的冗余信息,如果冗余信息正确，则B接受签名,否则拒绝.

2　Zhang方案安全性分析

2.1验证方程的错误分析

Zhang方案验证中m′=rh(cBx2)modn有误.方案希望cBx2=x1,但cB(x2,y2)=(x1,y1)不等价于cBx2=x1, cBy2=y1.可将上述1.3节中步骤3)更改为：计算X=(x2,y2)=s1P+s2P-rDA1-rDA2, cBX=(x3,y3), m′=rh(x3)modn.

2.2前向安全性分析

前向安全概念由Anderson于1997年首次提出[3],其思想是:如果签名者的私钥泄露，不会对之前的签名造成影响,即根据私钥无法恢复出消息明文.具有前向安全的椭圆曲线数字签名见文献[4-13].

Zhang方案中,若签名者的私钥cA1,cA2被泄露,攻击者截取签名(r,s1,s2)后,可由s1=(k1+rcA1) modn,s2=(k2+rcA2) modn计算出随机数k1,k2,则可计算出(k1+k2)DB=(x1,y1),进而可计算出消息m=rh(x1) modn,即此方案无前向安全性.

2.3第三方可恢复消息

签名者若否认签名,则接收者需要将解密后的签名提供给第三方进行验证,以揭示签名者的抵赖.方案中验证过程不需要使用接收者的私钥,任何第三方都可以进行验证,但由于消息恢复不需要接收者的私钥,第三方也可以恢复消息m,从而知道消息m中的内容,故方案公开验证时不具有消息机密性.

3　改进的签名方案

在保留Zhang方案使用双私钥、双参数的情况下,给出一个改进的签名方案,具有前向安全性、指定接收者消息恢复、第三方验证功能等性质.

3.1参数设置

参数设置同Zhang方案.

3.2签名过程

1)用户A任取k1,k2∈{1,2,…,n-1};

2)计算(k1+k2)DB=(x1,y1),r1=mh-1(x1) modn, (k1+k2)P=R,h(m)R=(x2,y2),r2=x2modn;

3)计算s1=(h(m)k1+r1cA1) modn,s2=(h(m)k2+r2cA2) modn.

消息m的签名为(r1,r2,s1,s2,R).

3.3消息恢复及验证

1)接收者B下载发送者A的公钥DA1,DA2;

2)检查r1,r2,s1,s2∈{1,2,…,n-1},错误则拒绝签名；

3)计算X=(x′,y′)=(s1+s2)P-r1(DA1+DA2),r′=x′modn,验证r′=r2是否成立；

4)计算cBR=(x″,y″),消息恢复m′=r1h(x″)modn；

若r′=r2成立且消息恢复m′有意义,则接受签名且m′=m,否则拒绝签名.

3.4正确性证明

因为X=(x′,y′)=s1P+s2P-rDA1-rDA2=h(m)(k1+k2)P,所以x′=x2,r′=r2.

因为(x″,y″)=cBR=cB(k1+k2)P=(k1+k2)DB=(x1,y1),所以x″=x1,m′=r1h(x″) modn=r1h(x1) modn=m.

4　改进方案的安全性及复杂度分析

4.1抗私钥攻击

攻击者截取签名(r1,r2,s1,s2,R)后,攻击者不知接收者的密钥cB,无法求出cBR,则无法恢复消息m.而由DB=cBP求解私钥cB需要求解椭圆曲线离散对数问题.

4.2前向安全性

改进方案中,若签名者的私钥cA1,cA2被泄露,攻击者截取签名(r1,r2,s1,s2,R)后,因无法通过计算私钥cB方式恢复消息m,故无法求出h(m),则由s1=(h(m)k1+rcA1) modn,s2=(h(m)k2+rcA2) modn不能计算出随机数k1,k2,从而无法由(k1+k2)DB=(x1,y1),r1=mh-1(x1) modn恢复出消息m.对文中改进方案而言，即使密钥泄漏,已有的签名也无法攻击,所以改进方案的前向安全性为绝对前向安全,比前述定期更换密钥具有的前向安全性更优.

4.3抗抵赖

签名者如果想抵赖签名,接收者可以把签名(r1,r2,s1,s2,R)提供给第三方,第三方可通过验证方程验证签名的正确性,防止签名者抵赖.验证过程不需要签名者的协助,也不需要提供恢复的消息.另外,在验证过程中,因不知接收者的私钥cB,第三方无法恢复出消息m,方案具有保密性.如有必要,接收方可提供私钥cB恢复消息m.

此外,验证者要想更改密钥cB以恢复出对自己有利的消息也是不可行的.设验证者希望恢复出对自己有利的消息为m,由m=r1h(x″)modn求出x″需求解单向函数问题,由cBR=(x″,y″)求解cB需求解椭圆曲线离散对数问题.

4.4抗伪造签名攻击

攻击者截取签名(r1,r2,s1,s2,R)后,随机选取椭圆曲线中点R′,组成(r1,r2,s1,s2,R′)发送给验证者,由3.3节验证过程,验证者可以验证r′=r2的正确性,进一步设cBR′=(x‴,y‴),验证者计算m=r1h(x‴) modn,则m为无意义的乱码,由3.3节则接收者拒绝签名.

另外,若攻击者事先选定某对其有利的消息m,若要满足验证条件需求出对应的x″,y″,R.由方程m=r1h(x″) modn求x″需求解Hash函数;(x″,y″)满足二次同余方程

y2=(x3+ax+b) modp,

由x″求解y″需求解该同余方程;由cBR=(x″,y″)求R需要求解出椭圆曲线离散对数双数学难题.

综上所述,该方案可抵抗攻击者伪造签名攻击.

4.5复杂度与安全性分析

对于基于椭圆曲线设计消息恢复数字签名,Yang等[14]于2011年提出了一个方案,但该方案没有前向安全性.同时具有前向安全性和公开验证消息机密性的方案,目前还没查到相关的文献.将文中方案与Yang方案进行复杂度对比,见表1.

表1　复杂度对比

[1]DIFFIEW,HELLMANM.Newdirectionincryptography[J].IEEE Transactions on Information Theory,1976,22(6):644.

[2]ZHANGYun-peng,CHENTong,ZHANGXian-wei,etal.Improveddigitalsignatureschemebasedonellipticcurve[J].Research Journal of Applied Sciences,Engineering and Technology,2012,4(18):3437.

[3]ANDERSONR.Tworemarksonpublickeycryptology[J].Computer and Communication Security,1997,19(9):128.

[4]张晓敏,张建中.基于椭圆曲线的前向安全代理签名方案[J].济南大学学报(自然科学版),2008,22(3):263.

[5]詹雄泉,洪景新.基于椭圆曲线密码体制的一种具有前向安全的数字签名方案[J].厦门大学学报(自然科学版),2005,44(2):189.

[6]付茂盛,任哲,侯整风.基于ECC的前向安全数字签名的研究与改进[J].计算机工程,2006,32(14):109.

[7]庞倩倩,辛小龙.两种具有前向安全的数字签名的改进方案[J].计算机工程与应用,2008,44(30):102.

[8]褚晶晶,何琪芬,张慧.前向安全的由指定接收者恢复消息的签名方案[J].杭州师范大学学报(自然科学版),2010,9(5): 335.

[9]徐光宝,姜东焕,梁向前.一种强前向安全的数字签名方案[J].计算机工程,2013,39(9):167.

[10]胡江红.一类前向安全签名方案的安全性分析[J].电子设计工程,2015,23(14):23.

[11]曹欣,魏仕民,卓泽朋.三个前向安全代理签名方案的安全性分析[J].计算机工程与应用,2015,51(7):98.

[12]戚明平,陈建华,何德彪.具有前向安全性的可公开验证的签密方案[J].计算机应用研究,31(10):3093.

[13]陈宁宇,楼俊刚.一个基于身份的前向安全代理签名的安全分析与改进[J].计算机应用与软件,2014,31(8):295.

[14]杨迎辉,任俊峰,袁喜凤.改进的具有消息恢复签名方案[J].计算机技术与发展,2011,21(4):168.

(责任编辑惠松骐)

Attack analysis and improvement on a digital signature algorithm with message recovery

ZHOU Ke-yuan

(The Second Department,Suqian College,Suqian 223800,Jiangsu,China)

The digital signature algorithm with message recovery proposed by Zhang Yun-peng et al is analyzed,two errors are pointed out,the algorithm didn’t have the forward security,and one can recover message.An improvement algorithm is proposed,the correctness,security are proved.

discrete logarithm;elliptic curve;digital signature;message recovery;replacement message attack

10.16783/j.cnki.nwnuz.2016.04.009

2015-06-06;修改稿收到日期:2015-09-29

宿迁市科研项目(Z201450)

周克元(1978—)，男，江苏淮安人，讲师，硕士.主要研究方向为密码学.

E-mail:zhoukeyuan2001@163.com

TP 309.7；TN 918.1

A

1001-988Ⅹ(2016)04-0038-03