高一数学测试



○课外测试○

高一数学测试

一、填空题(本大题共14小题,每小题5分,共70分)

1.函数y=ln(x+1)的定义域是______.

4.已知变量x,y满足

则z=x-y的最小值为______.

5.已知等比数列{an}的前n项和Sn=3n+a,则a=______.

10.已知数列{an}的通项公式为an=n2-2an(n∈N*),且当n≠4时,an>a4,则实数a的取值范围是______.

12.已知l,m,n为两两不重合的直线,α,β,γ为两两不重合的平面,给出下列4个命题:

① 若α∥β,l⊂α,则l∥β;

② 若α⊥γ,β⊥γ,则α⊥β;

③ 若m⊄α,n⊂α,m∥n,则m∥α;

④ 若m⊂α,n⊂α,m∥β,n∥β,则α∥β.

其中命题正确的是______.(写出所有正确结论的序号)

14.已知函数f(x)=ex,对于实数m、n、p有f(m+n)=f(m)+f(n),f(m+n+p)=f(m)+f(n)+f(p),则p的最大值是______.

二、解答题(本大题共6道题,计90分.解答应写出必要的文字说明、证明过程或演算步骤)

15.(本小题满分14分)已知等差数列{an}中,a3=8,a6=17.

(1) 求a1,d;

(2) 设bn=an+2n-1,求数列{bn}的前n项和Sn.

16.(本小题满分14分)如图,在三棱柱ABC-A1B1C1中,D是BC的中点.

(1) 若E为B1C1的中点,求证:BE∥平面AC1D;

(2) 若平面B1BCC1⊥平面ABC,且AB=AC,求证:平面AC1D⊥平面B1BCC1.

(1) 求sin 2α的值;

(2) 求β的大小.

(1) 求B的大小;

(3) 若b=6,求∆ABC面积的最大值.

19.(本小题满分16分)如图,是一块足球训练场地,其中球门AB宽7米,B点位置的门柱距离边线EF的长为21米,现在有一球员在该训练场地进行直线跑动中的射门训练.球员从离底线AF距离x(x≥10)米,离边线EF距离a(7≤a≤14)米的C处开始跑动,跑动线路为CD(CD∥EF),设射门角度∠ACB=θ.

(1) 若a=14,

① 当球员离底线的距离x=14时,求tanθ的值;

② 问球员离底线的距离为多少时,射门角度θ最大?

20.(本小题满分16分)已知数列{an}满足a1=1,an+1=2an-3(-1)n(n∈N*).

(1) 若bn=a2n-1,求证:bn+1=4bn;

(2) 求数列{an}的通项公式;

(3) 若a1+2a2+3a3+…+nan>λ·2n对一切正整数n恒成立,求实数λ的取值范围.

参考答案

一、填空题

4.-2；5.-1；6.48；7.9；

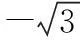
二、解答题

a1=2,d=3.

(2) 由(1)可得an=3n-1,

所以bn=3n-1+2n-1,

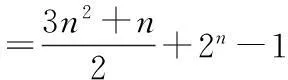
16.(1) 在三棱柱ABC-A1B1C1中,

D是BC的中点,E为B1C1的中点,

又BE⊄平面AC1D,DC1⊆平面AC1D，

所以BE∥平面AC1D.

(2) 因为在∆ABC中,D是BC的中点,且AB=AC,所以AD⊥BC.

因为平面B1BCC1⊥平面ABC,AD⊂平面ABC,

平面B1BCC1∩平面ABC=BC,

所以AD⊥平面B1BCC1.

又AD⊂平面AC1D,所以平面AC1D⊥平面B1BCC1.

所以cosβ=cos[α-(α-β)]

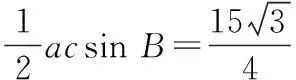
∵b2=a2+c2-2accos B，

∴49=(a+c)2-ac,

∴a+c=8.

(3)∵b2=a2+c2-2accos B，

∴36=a2+c2+ac≥2ac+ac,

19.在∆ACD中,设∠ACD=α,则

在∆BCD中,设∠BCD=β,则

所以tanθ=tan(α-β)

(1) 当a=14时,AD=14,BD=7.

① 若x=14,则

所以当x=10时射门角度θ最大.

(2) AD=28-a,BD=21-a,

则-x2+21x=a2-49a+28×21.

因为7≤a≤14，所以

98≤a2-49a+28×21≤294,

则98≤-x2+21x≤294,

解得7≤x≤14.

又x≥10,所以10≤x≤14，

所以x的取值范围是[10,14].

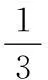
②当球员离底线的距离为10时，射门角度θ最大;

20.(1)bn+1=a2n+2-1

=2a2n+1-3(-1)2n+1-1

=2a2n+1+2

=4a2n-6(-1)2n+2

=4a2n-4=4bn.

(2)a2=2a1-3(-1)=5,

b1=a2-1=4.

所以{bn}是等比数列，

所以bn=4n=a2n-1.

a2n=4n+1=22n+1,

a2n=a2n-1+3=22n+1,

a2n-1=22n-1-1.

即an=2n+(-1)n.

(3)由(2)有nan=n·2n+(-1)n·n,

所以Sn=a1+2a2+3a3+…+nan

=(1·21)+(2·22+2)+…

+(n·2n+(-1)n·n)

=(1·21+2·22+…+n·2n)

+(-1+2-3+…+(-1)n·n).

令S=1·21+2·22+…+n·2n，则

2S=1·22+2·23+…

+(n-1)·2n+n·2n+1.

相减得-S=21+22+…+2n-n·2n+1

∴S=(n-1)·2n+1+2.

当n为奇数时，

T=-1+2-3+…+(-1)n·n

当n为偶数时，

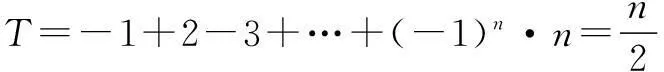
所以当n为奇数时，

Sn=S+T

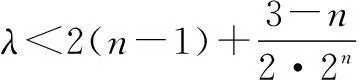
当n为偶数时，

Sn=S+T