基于支持向量机原理的连铸板坯表面温度预测模型

创新者：张兆雄

基于支持向量机原理的连铸板坯表面温度预测模型

创新者：张兆雄

提出了一种基于支持向量机理论的连铸板坯表面温度预测模型。结合连铸的过程工艺特性以及历史过程数据，以过热度、拉坯速度、二次冷却水量、二冷区出口位置温度作为模型的输入，通过支持向量机回归算法原理，对二冷区内的铸坯表面温度进行预测，在此基础上用粒子群算法对支持向量机的惩罚系数c和核函数宽度进行寻优，以提高模型预测精度，并利用MATLAB软件进行仿真测试。结果表明该方法预测精度较高，是一种有效的温度预测方法，利于提高铸坯的生产质量。

铸坯在二冷区的表面温度的确定，对制定合理的冷却制度，提高铸机产量和铸坯质量都是十分重要的。而二冷区受冷却水雾、水汽以及铸坯表面随机生成的氧化铁皮的影响，测量环境恶劣，测温装置几乎无法准确和长期地对铸坯表面真实温度进行测量，到目前为止还没有相应的温度检测仪表用于铸坯表面温度的闭环控制。目前了解铸坯二冷区的温度分布都是通过建立的连铸坯稳态凝固传热的机理模型，进而了解铸坯的凝固传热过程。实际上，受设备、工艺流程和生产节奏等因素的影响，在连铸的生产过程中，拉坯速度、水量、传热系数等工艺参数经常发生变化，特别是方坯连铸机，其变化更为频繁，过于依赖人工经验，使得基于稳定条件下建立的凝固传热模型在应用过程中无法准确计算铸坯的温度场分布，无法作为二连铸冷动态控制的基础，影响铸坯的生产质量。因此，对连铸铸坯在二冷区内表面温度的准确预测，对提高铸坯的产量和质量具有重大的意义。近年来，有学者将支持向量机技术运用于工业场合的温度预测，取得了一定的突破。

支持向量机回归原理

支持向量机（Support Vector Machine）最早是由Vapnik提出，最早是用于解决模式识别中线性不可分的两类分类问题而诞生的，后人为了解决线性和非线性函数的回归问题，引入了不敏感损失函数和核函数的概念。

支持向量机回归（Support Vector Regression，简称SVR）分为线性回归和非线性回归两种，本文主要介绍非线性回归的基本原理。假设训练样本集为，其中xi表示第i个训练样本的输入向量，；yi表示输出的期望值；l表示样本个数。支持向量机回归问题的目的就是通过对训练样本集x的训练，找到一个实值函数f（x），使其满足，并且误差要保持在一定的范围内。在支持向量机回归理论中， 针对非线性样本集，要先构成一个非线性映射，通过这个非线性映射将原始的样本数据空间映射到一个高维特征空间中，可以通过利用这个高维空间中线性化的样本集

来构成线性回归估计函数。据此，在非线性条件下，可构造下面形式的回归估计函数。式中，。

与线性情况类似，非线性情况下的最优化问题为：

通过求解上式，则能够得到非线性回归问题的超平面法向量和回归估计函数，它们分别为：

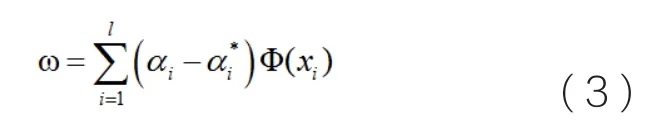
核函数的作用是可以避免在高维特征空间中直接求解非线性映射）。常见的核函数有线性核函数：多项式核函数：径向基核函数：

对女性的崇拜书写是《你眼睛的弧线》的“行为”修辞。在艾吕雅看来，能量、活力的交换不仅是自我存在的必要条件，也是人与自然亲近的必要条件。因而，爱的活动交流同样存在于人与自然之间。这种泛爱论的思想首先体现在将自然界的活力与女性活力进行类比的过程之中。正如我们上文分析的，《你眼睛的弧线》中，女性的形象常和自然的基本成分——水、土、植物、阳光互相对照比喻。对自然的描写总是呈现出女性躯体的轮廓。而女性原型历来就可以是山川、海洋、树木花草的象征，于是，女性与自然二者浑然一体。女性的无处不在说明了作者对女性的崇尚最终使得人类渐渐取代了上帝的位置，拥有造物的神力，符合当时“上帝已死”的观点。

铸坯表面温度预测模型的建立

模型输入输出的选择

（1）针对本文的研究内容，模型的输出应为二冷区内的铸坯表面温度，从理论上讲，二冷区铸坯表面有无数个温度点，要预测每一点的温度是难以实现的。本文所研究的某方坯连铸机在二冷区有四个冷却段，每个冷却段靠该段的流量调节阀控制水量。本文将各冷却段末端的铸坯表面温度作为目标预测温度。

（2）模型的输入变量应选择那些对铸坯表面温度具有较大影响的变量，同时在应用中还要考虑经济性、稳定性、可行性及后期维护等其他因素的限制，对变量的检测方法、位置和精确度等需有一定程度的要求。经分析和调研，决定将铸坯过热度、拉坯速度、二冷区各冷却段配水量和二冷出口位置铸坯温度作为输入变量来对目标温度进行预测。

数据的采集及预处理

（1）模型对温度进行预测的基础是基于大量的历史过程数据的，通过数据来进行自学习，找出输入和输出之间的关系。本文所用的训练数据均取自于连铸现场，连铸机的弧形半径为8m；结晶器长度为0.95m，有效长度为0.85m；冷却段第一段长度0.28m，第二段长度1.8m，第三段长度2.2m，第四段长度2.2m。

（2）连铸现场的数据都是通过测得的各项工艺参数经传热模型计算得到的铸坯表面各点的温度。这些数据过。于冗杂，包含了铸坯表面各个点的温度，涉及了众多不相干的变量，选择课题所需要的变量，即浇铸温度、拉坯速度、二冷区四个冷却段的水量、各段段末温度及测量点温度。

训练数据必须要涵盖生产过程中各变量所有可能的变化范围，在选择上要尽可能的扩大数据范围和多样性。在收集得的数据中，因为测量仪器和测量环境方法等原因，会有一些数据出现部分丢失，误差较大、前后不对应、重复混乱等现象。这些数据必将影响模型的性能，因此必须对其进行清理，经筛选，最终整理为500组输入输出数据，作为模型的训练集。

（3）因为变量的类型不同，数据的不同数据组间必然存在着量纲不同、数量级跨度较大的情况。因此为了建模需要，要对这些数据进行归一化预处理，以消除数据因不同量纲和不同数量级所带来的影响。本文采用区间映射法对数据进行归一化处理，其计算公式为。

粒子群对参数的寻优

（1）粒子群算法（PSO）将所求问题的所有可能解类比于鸟群捕食运动中所有食物的位置。种群中的每一个粒子表示所求问题的一种可能解，每个粒子各自有自己的适应度，其值由适应度函数决定。粒子速度在过程中会进行动态调整，它决定了粒子的移动距离和方向，从而实现了算法在解空间中进行寻优的过程。

（2）本文所建立的SVR预测模型选用径向基核函数，其中惩罚系数 c和径向基核函数宽度的取值对模型的预测性能有很大的影响。本文利用粒子群算法来对参数c和进行寻优，粒子群中的每个粒子代表着模型中可能的参数c和，通过适应度函数计算粒子适应度值，本文将对训练集进行预测的准确率作为粒子群优化中的适应度函数值，准确率越高适应度越好。优化步骤如下：

（b）计算每个粒子的适应度值；

（d）按式（7）和式（8）更新粒子的速度和位置；

（e）判断粒子适应值是否满足终止条件，如不满足，返回步骤（2）重新计算适应度值，直到满足终止条件，输出，即最优参数c和，计算结束；（f）SVR 预测模型在最优参数c、下进行温度预测。

图1 T3预测值与实际值对比图

仿真结果及分析

利用MATLAB软件建立模型进行仿真测试。选取数据的前400组作为训练集，后100组作为测试集，选择均方误差作为模型的评判指标，检验模型性能，其公式为：

将预测值与实际值的均方误差整理到表1中。

表1 目标温度点预测均方误差

从表1可以看出，各预测点的均方误差都在4以下，第四冷却段末端的预测均方差是四个点中最小的，第二、三、四冷却段末端的均方误差依次略有增加，这是因为越靠近二冷出口测温位置的预测点，与测温点的联系就越紧密，预测精度越高。

以预测点T3为例，将预测值和实际值放在同一坐标图中进行对比，如图1所示。图中，横坐标为样本个体，纵坐标为预测的温度值，蓝色实心点为样本的实际值，绿色空心点为样本的预测值。

由图可见，预测值能够跟随实际值的变化而波动，表现出了很好的适应性，同时保持了较高的精度，两者相差无几。

结语

本文针对连铸生产中二冷区内铸坯表面温度的确定问题，进行了基于支持向量机回归算法的预测模型的建立。模型中的惩罚系数c和核函数参数是重要的参数，其值决定着模型的预测性能，并且与模型的输入输出没有直接的联系，本文采用粒子群算法对两者进行寻优，提高了模型预测精度。试验结果表明该模型有着较高的预测精度，是一种十分有效的建模方法，能够根据工艺变化情况，对目标温度进行实时准确的预测，有利于提高铸坯的质量。

DOI：10.3969/j.issn.1001-8972.2016.06.017