基于多目标渐进优化法的深孔机床床身重构设计*

阴书玉　薄瑞峰　沈兴全

(①中铁工程装备集团有限公司,河南 郑州 450016;②中北大学机械与动力工程学院,山西 太原 030051)



基于多目标渐进优化法的深孔机床床身重构设计*

阴书玉①薄瑞峰②沈兴全②

(①中铁工程装备集团有限公司,河南 郑州 450016;②中北大学机械与动力工程学院,山西 太原 030051)

为了有效提高深孔机床床身静动态性能及实现其轻量化设计，将多目标拓扑优化技术引入到床身的结构设计中。首先以渐进结构优化法(ESO算法)为理论基础，利用ANSYS软件提出了以整体刚度和基频共同最大化为综合目标的多目标渐进结构优化算法；其次运用该算法对深孔钻床床身进行拓扑优化，获得了最佳的拓扑图样；最后，依据优化后的拓扑图样对其进行了重构设计。分析结果显示：该算法能够较好地完成优化目的，即优化后床身的静、动态性能得到了有效的提高，同时整体重量明显地下降，达到了轻量化设计的要求，为企业提供了更为合理的床身结构设计方案。

多目标渐进优化法；深孔机床；床身；ANSYS；重构设计

传统的经验结构类比分析方法存在较大的缺陷，已经很大程度上不能符合现代深孔加工机床的设计要求。从机床结构设计角度来讲，如何有效提高机床基础部件(床身、主轴箱等)的静动态性能以及实现其轻量化设计对改善整机性能有着重要的作用[1]。研究表明：多目标结构拓扑优化技术为结构方案设计提供了一种有效的解决方案。作为结构拓扑优化领域中重要的一种方法，渐进结构优化法(ESO算法)简单易行，以其为基础的多目标拓扑优化算法容易利用现有的有限元分析软件实现，具有很好的通用性。

童水光等人以多目标拓扑优化为理论依据，对卧式旋压机床身筋板的布局进行了优化研究,取得了良好的优化效果[2]。汪兵兵等人以某机械基础结构作为研究对象，分别利用一般经验设计方法与多目标拓扑优化方法对其内部筋板布局进行研究，分析表明拓扑优化方法可以获得更好的优化效果[3]。需要说明的是上述多目标拓扑优化都是基于SIMP法进行研究的，而基于ESO算法的多目标拓扑优化几乎还未在机床结构优化领域得到研究与应用。

考虑到多目标优化问题广泛存在于实际结构拓扑优化领域中，本文以渐进结构优化法为基础，以ANSYS为开发平台，对多目标拓扑优化算法及其在Z8016深孔钻床床身上的应用进行深入的研究。

1　多目标优化数学模型描述

本文中的多目标拓扑优化问题是在多载荷工况下以最大刚度和最大基频为综合优化目的进行研究分析的。其优化数学模型如下所示：

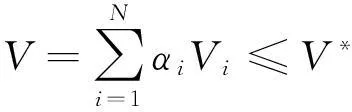
i=1,2,…N

(1)

式中：C表示结构的总应变能；V表示优化后的体积；V*表示允许的结构总体积上限；Vi表示第i个单元的体积；αi为设计变量，取0和1(0代表删除单元，1代表保留单元)。

2　多目标渐进结构优化算法

渐进结构法的基本思想:逐渐删除初始设计结构中的无效或低效材料(单元)，使最终优化结构能够取得最佳的承载特性[4-5]。

2.1多目标单元灵敏度公式的推导

对于多目标渐进结构优化法而言，如何准确推导出基于刚度和频率的多目标单元灵敏度公式是算法的关键之处。刚度和频率是两种不同性质的单元灵敏度，因此需要对其进行归一化处理,才能准确求出多目标灵敏度。

多工况下的单元刚度灵敏度公式可依据文献[6]中的相应公式求得。

经归一化处理的单元刚度灵敏度αNsi表示为：

(2)

式中：αi表示多工况刚度灵敏度，αimax及αimin分别表示多工况下的最大及最小刚度灵敏度。

单元频率灵敏度公式可依据文献[7]中的相应公式求得。

同理，经归一化处理的频率单元灵敏度αNdi表示为：

(3)

式中：αimax及αimin表示单元的最大及最小频率。

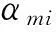
(4)

式中：λ1、λ2分别表示刚度、频率的权重因子；sfs、sfd分别表示平衡静动态优化的比例因子——用来将归一化的刚度灵敏度值和频率灵敏度值进行平均化处理，使两者能够被合理化处置。

2.2多目标渐进优化算法的迭代步骤

本节中的单元删除是利用ANSYS中的“单元生死”功能实现的[8]，对于多目标优化问题的材料删除准则的表达式可表示为：

αmi≤αmimax×RRi

(5)

RRi+1=RRi+ERi=0,1,2…

(6)

式中：αmi是多目标单元灵敏度；αmimax是最大的多目标单元灵敏度；RRi为删除率，ER是进化率。

图1表示通过在ANSYS平台上实现体积约束下的多目标渐进优化方法的迭代步骤流程图。

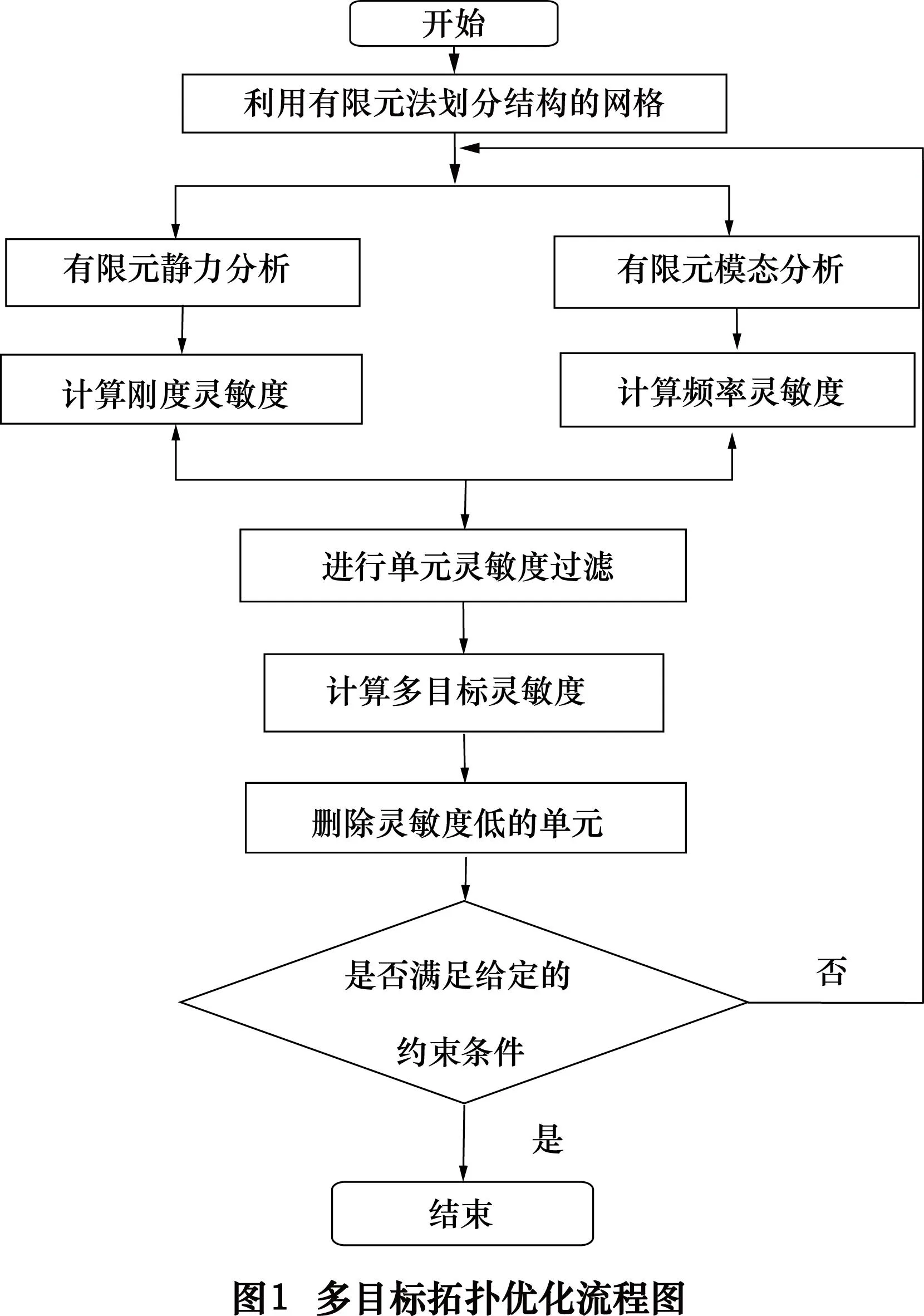
3　床身的多目标拓扑优化

由于床身结构的固有频率和应变能属于两种不同性质的概念，仅对床身进行多工况拓扑优化很难获得结构的最佳拓扑构型，因此非常有必要对深孔机床床身进行多目标拓扑优化研究。

需要指出的是本文是在文献[6]的基础上进行进一步研究分析的，因此有关深孔机床床身有限元模型的建立以及床身载荷工况及约束条件的分析与参考文献[6]相同，在此不再赘述。

3.1床身的ESO法优化结果

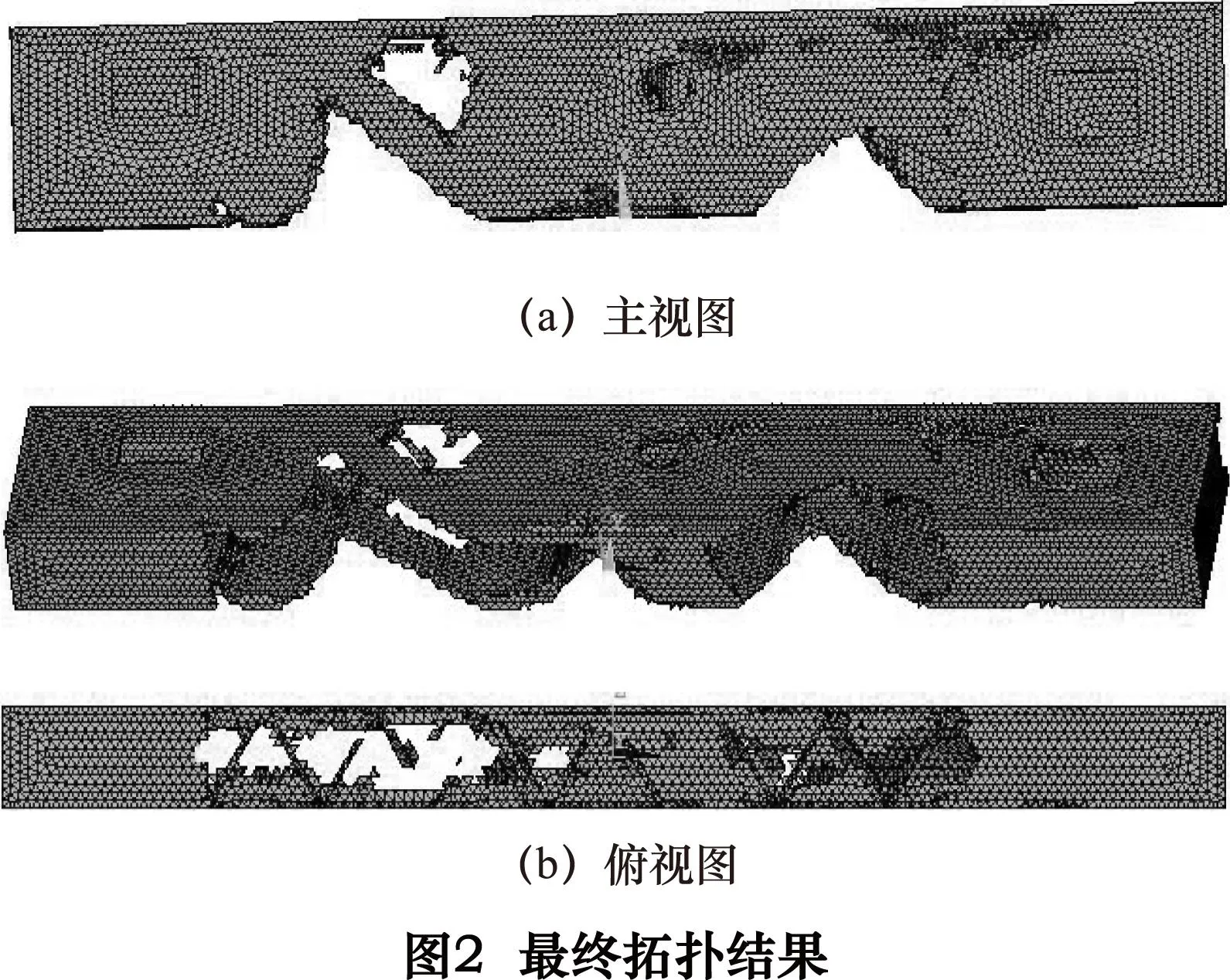
由图2可以看出，对床身进行基于最大刚度及基频的多目标拓扑优化后，床身的两端部分材料属于高效单元，被保留下来；中间结构材料大多数属于低效单元，依据单元删除准则其被逐渐删除。最终经过83次迭代，形成如图2所示的最优拓扑图样。

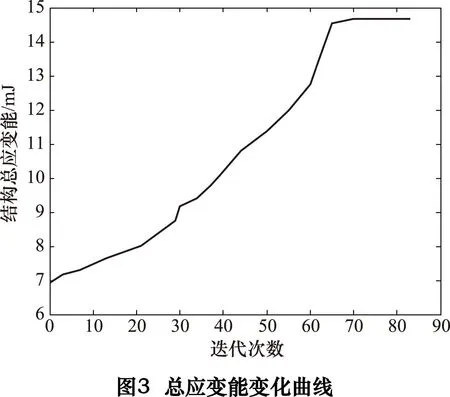
拓扑优化过程中的结构总应变能曲线图、迭代次数与lgD的关系曲线、前三阶固有频率变化曲线、体积比和性能指标变化曲线分别如图3～6所示(D表示3种工况中最大与最小应变能密度比值的平均值)。

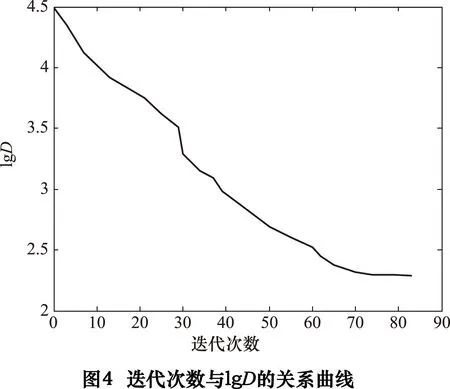
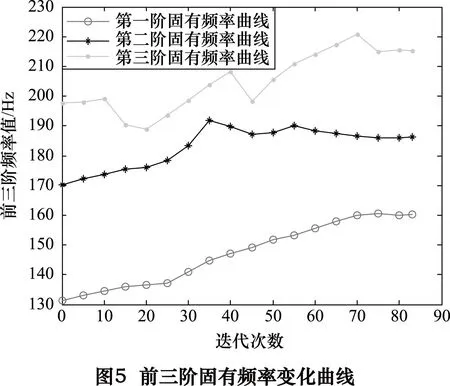
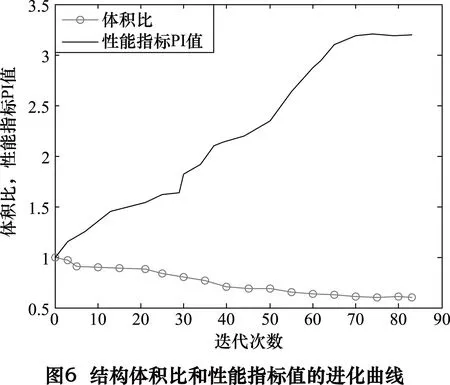
从图3可知，结构总应变能并非随着迭代次数的增加而逐渐减小，相反而是缓慢增加最后达到一个稳定的状态，本节中所研究的应变能最优化是指在满足体积约束下进行的。从图4可知，lgD的值由最初的4.49减小到最终的2.1，即最大与最小应变能密度的差距显著减小，这充分反映了利用该算法能够优化床身的应变能(刚度)。从图5可知，第一阶固有频率随着迭代次数的不断增加而逐渐得到提高，尽管第二、三阶固有频率在迭代过程中有所波动，但最终还是得到了提高，同样这反映了利用该算法能够较好地优化床身的低阶频率。

由图6可以看出优化迭代次数达到69次左右的时候，结构其实已经获得了最优的拓扑图样，即刚度和频率共同达到了最优化。然而此时优化过程并未终止，直到迭代次数变为83次时，整个进化过程才结束，这说明该多目标拓扑优化算法应用到深孔机床床身上时其迭代效率还存在一些缺陷，该算法本身还有待进一步地改进。除此之外，该算法还是较好地完成了床身的多目标拓扑优化，为下一步床身的重构设计提供了理论指导依据。

3.2床身的重构设计

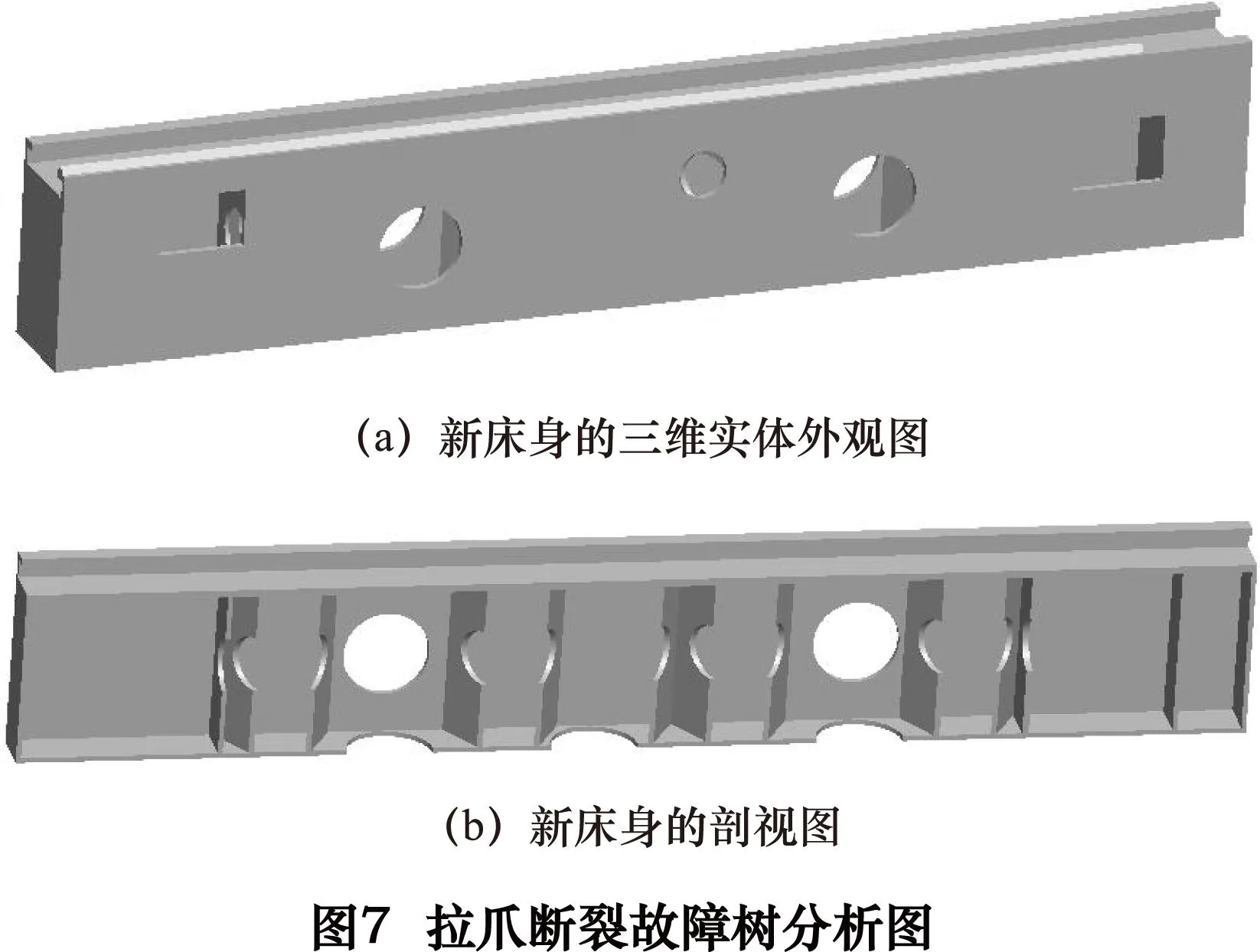
合理地选取床身内部筋板的布局方式及筋板孔尺寸的大小,不仅可以增强床身静动态性能,而且能够节约材料以及减小生产成本[9]。因此考虑上述最优拓扑图样和制造工艺对原床身采用以下改进措施：(1)增加床身前后端横向筋板数，减少床身中间部分的筋板数(中间V型筋板数由原来的7组减少为4组)。(2)筋板孔直径由100 mm变为250 mm。(3)在床身两侧壁上开孔[10]。(4)下底板厚度从最初的25 mm减小为18 mm并在其上开3个圆形孔，圆孔直径为350 mm。经过反复验证，重构设计后床身的新结构如图7所示。

对优化前后的床身结构进行静力分析及模态分析，相关结果如表1所示。

表1优化前后床身性能指标的比较

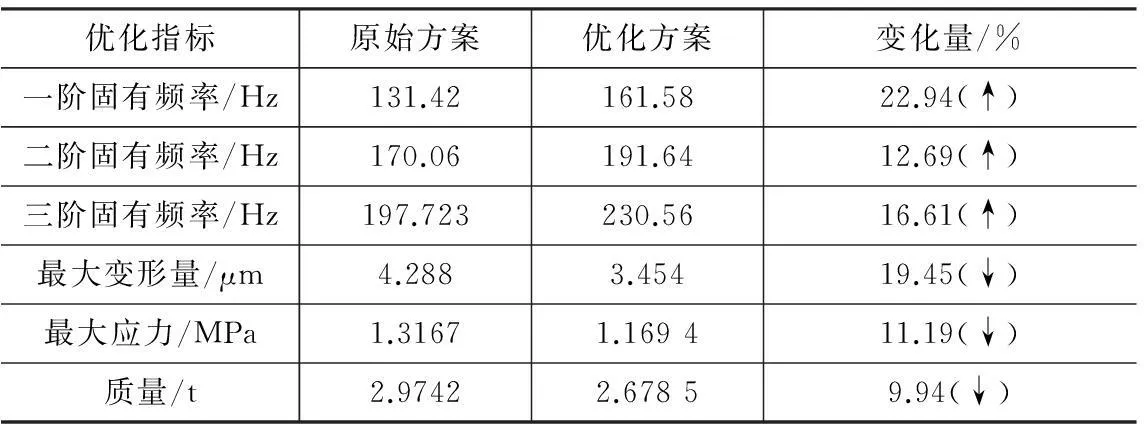
优化指标原始方案优化方案变化量/%一阶固有频率/Hz131.42161.5822.94(↑)二阶固有频率/Hz170.06191.6412.69(↑)三阶固有频率/Hz197.723230.5616.61(↑)最大变形量/μm4.2883.45419.45(↓)最大应力/MPa1.31671.169411.19(↓)质量/t2.97422.67859.94(↓)

如表1所示，与原结构相比，最终优化方案的前三阶固有频率依次增加了22.94%，12.69%，16.61%，且远离工作频率，避免发生共振现象，其动态性能得到了有效地改善；床身的最大变形量、最大等效应力分别降低了19.45%、11.19%，即其静态性能也得到了极大程度的提高；与此同时床身的质量减小了9.94%，降低了制造成本，实现了轻量化设计的目的。

4　结语

(1)利用ESO算法以及ANSYS开发平台，实现了多载荷工况下基于刚度及基频共同最优化的多目标渐进结构优化算法。

(2)运用该算法对深孔钻床床身进行了多目标结构拓扑优化，获取了较好的拓扑图样。优化后床身的静、动态性能均得到了有效的提高，质量显著下降，实现了其减重的目的。

(3)在对床身进行拓扑优化时，该算法的迭代效率还存在一些缺陷，其理论本身还有待进一步地改进。

(4)本文所研究的内容进一步拓宽了结构拓扑优化理论及其应用范围。该设计方法为其地类似零部件的创新优化提供了一定的指导意义，具有较好的工程应用前景。

[1]张宏博.深孔钻床关键件动态性能分析与结构拓扑优化[D].太原:中北大学,2013.

[2]童水光,刘彧,张健,等.基于拓扑优化的卧式旋压机床身加强肋布局优化设计方法[J].机械设计,2012,29(6):31-35.

[3]汪兵兵,丁晓红,孙晓辉,等.机械基础结构多目标拓扑优化设计方法[J].包装工程,2013,34(15):15-19.

[4]Huang X,Xie Y M.Evolutionary topology optimization of continuum structures[M].Australia:Wiley,2010.

[5]Zuo Z H,Xie Y M.Evolutionary topology optimization of continuum structures with a global displacement control[J].Computer-Aided Design,2014,56:58-67.

[6]阴书玉,薄瑞峰，闫帅印，等.基于ESO算法的深孔机床多工况拓扑优化[J].制造技术与机床,2014(8):69-73.

[7]茅志颖.结构动力学设计渐进优化方法研究[D].南京:南京航空航天大学,2010.

[8]博弈创作室.APDL参数化有限元分析技术及其应用实例[M].北京:中国水利水电出版社,2004.

[9]徐燕申,张兴朝,牛占文,等.基于元结构和框架优选的数控机床床身结构动态设计研究[J].机械强度,2001,23(1):1-3.

[10]倪晓宇,易红,汤文成.机床床身结构的有限元分析与优化[J].制造技术与机床，2005(2):47-50.

如果您想发表对本文的看法，请将文章编号填入读者意见调查表中的相应位置。

Reconstructional design for deep hole machine lathe bed based on multi-objective evolutionary optimization

YIN Shuyu①, BO Ruifeng②, SHEN Xingquan②

(①China Railway Engineering Equipment Group Co.,Ltd., Zhengzhou 450016, CHN;②School of Mechanical and Power Engineering, North University of China, Taiyuan 030051, CHN)

In order to improve the static and dynamic performance and achieve the lightweight design for deep hole drilling machine lathe bed effectively, the multi-objective topology optimization was introduced to the structural design of lathe bed. Firstly, based on the theory of evolutionary structural optimization(ESO), multi-objective evolutionary optimization algorithm based on optimization goal of maximum stiffness and maximum fundamental frequency was established by ANSYS software. Secondly, structural topology optimization design for deep hole drilling machine lathe bed was realized by the algorithm, and the optimal topology structure was gained. Finally, depending on the optimization program, the model of lathe bed was redesigned. From the optimization results, optimization purposes are implemented well by the algorithm. That is to say, the static and dynamic performance of the optimal lathe bed have been improved effectively, and its overall weight is decreased obviously, reaching the requirement of lightweight design. It can provide the more reasonable structure plan of the lathe bed for the enterprise.

multi-objective evolutionary optimization; deep hole machine; lathe bed; ANSYS; reconstructional design

TH122

A

阴书玉，男，1988年生，硕士研究生，研究方向为有限元分析及结构拓扑优化，已发表1篇论文。

(编辑李静)(2015-08-18)

160315

*国家自然科学基金(51175482)； 国家国际科技合作专项项目(2013DFA70770)；山西省回国留学人员科研资助项目