基于Simulink的绕线式异步电机串级调速系统虚拟实验分析

张厚升, 于兰兰, 孟天星, 姜吉顺

(山东理工大学 电气与电子工程学院, 山东 淄博　255049)



基于Simulink的绕线式异步电机串级调速系统虚拟实验分析

张厚升, 于兰兰, 孟天星, 姜吉顺

(山东理工大学 电气与电子工程学院, 山东 淄博255049)

将Matlab/Simulink引入课程的虚拟实验教学之中。利用Simulink建立了双闭环控制的绕线式异步电机串级调速系统仿真模型,给出了仿真参数,利用仿真结果分析了串级调速系统的启动过程、突加负载和转速给定值改变时的动态调节过程,验证了该调速系统仿真模型的正确性。在实验教学中,Simulink仿真模型辅助学生对系统动态调节过程的理解、建立系统级控制思想,也可用于研究和开发异步电机串级调速系统。

异步电机； 串级调速； 仿真模型； Simulink

运动控制系统[1-5]是高校自动化、电气工程等专业的重要专业基础课程,串级调速是其中很重要的内容。绕线式异步电机的特点是转子绕组可以外接电阻或者附加电动势[4-10],通过调节外接电阻或附加电动势来限制异步电机的启动电流或调节异步电机的转速。因为串电阻调速的方法要消耗系统功率,因此效率比较低[11-14],一般用于有级调速。采用整流技术的串级调速,可将异步电机转差功率经过变换器回馈到交流电网,不仅可以减小转差功率的损耗、减少网侧的谐波含量和提高系统效率,而且还可以实现无级调速,有更好的调速性能。

现行专业教材中,主要是针对串级调速系统的原理、类型、机械特性等进行理论分析,而对于动态调速过程很少涉及。本文在分析绕线式异步电机串级调速系统基本结构与原理的基础上,借助Simulink仿真软件,建立了系统的仿真模型,利用仿真实验得到的波形分析串级调速系统的启动过程、突加负载过程和改变电压给定值时的动态调速过程,旨在拓展现有教材内容,让学生加深对双闭环控制的串级调速系统的理解和开展深入研究。

1　绕线式异步电机串级调速系统及工作原理

双闭环控制的绕线式异步电机串级调速系统的结构如图1所示。该调速系统由主电路和控制电路两大部分组成:主电路包括绕线式异步电机、二极管不控整流器、晶闸管逆变器、变压器等；控制电路包括转速和电流的检测与反馈装置、电压给定环节、转速调节器(ASR)、电流调节器(ACR)、晶闸管脉冲触发电路等。转速反馈信号由测速发电机环节检测与转换,由电流互感器对逆变器交流侧的电流进行实时检测并进行反馈[3]。改变转速给定的电压信号,可以实现对串级调速系统转速的设定与调节。双闭环控制的绕线式异步电机串级调速系统可以通过改变逆变角β的大小来控制转子电流,进而实现调速。

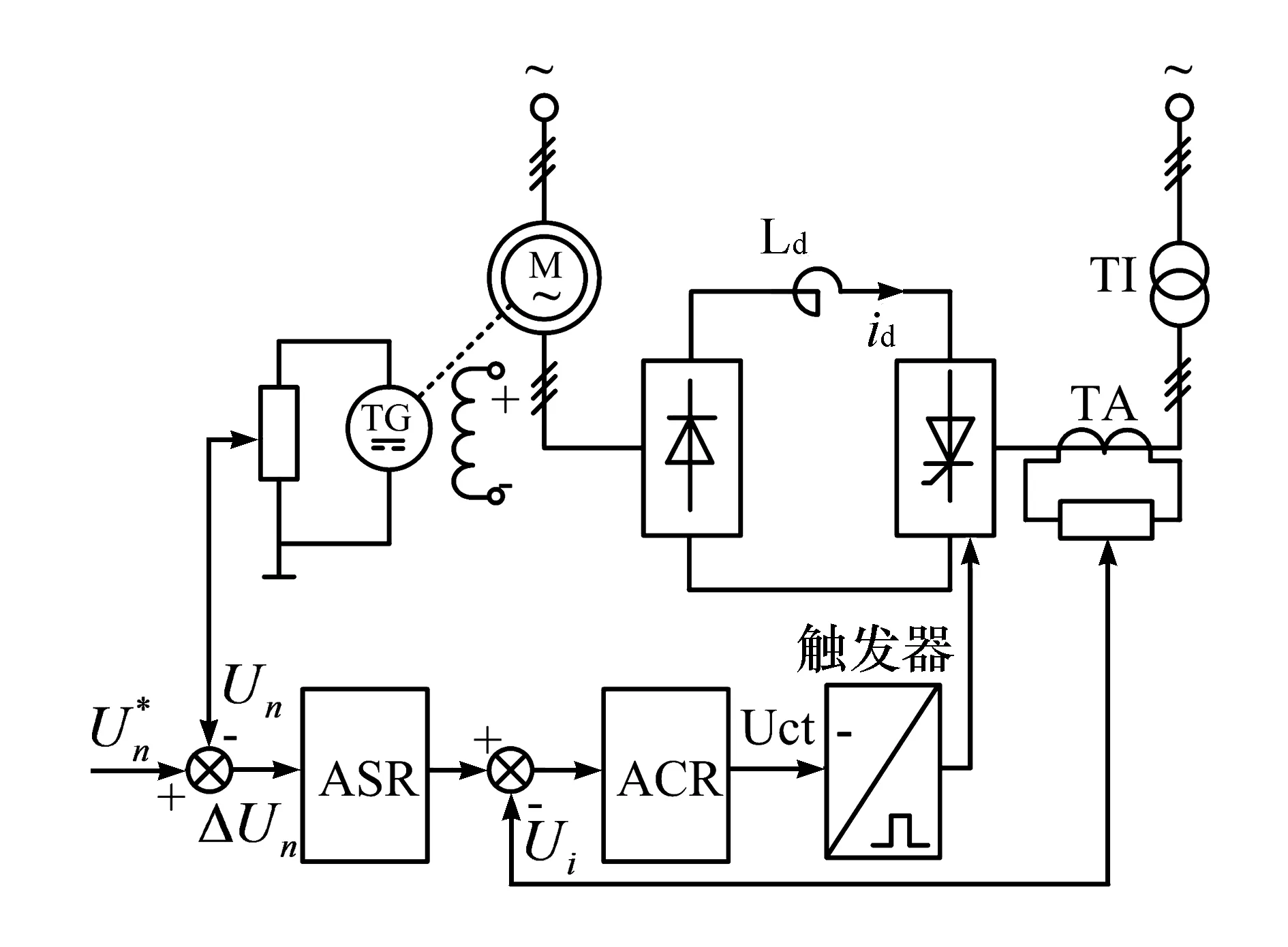
图1　双闭环控制的绕线式异步电机串级调速系统结构图

在调速系统中,平波电抗器Ld的作用是平滑电流id。在这种调速方式中,转子转差功率经过二极管不控整流器、晶闸管逆变器和变压器回馈电网,所以属于

异步电机转差功率馈送型调速系统[11],系统的效率比较高,属于节能的交流调速方式。为了有效地防止逆变颠覆,在电流调节器ACR输出电压为0 V时,需要设定最小逆变角βmin。ASR和ACR均采用PI调节器,可以实现转速、电流的无静差调节。该串级调速系统具有静态稳速与动态恒流的作用。

2　仿真模型与仿真参数

2.1Simulink仿真模型

利用Matlab/Simulink建立的双闭环控制的串级调速系统的仿真模型如图2所示。该仿真模型由主电路和控制电路两部分组成。

主电路部分的三相交流电源采用3个正弦电压源模块usa、usb和usc；异步电机采用Asynchronous Machine SI Units；整流装置采用2个多用桥模块,即二极管整流器模块Diode和晶闸管逆变器模块inverter；三相变压器模块采用Three-Phase Transformer (Two Windings)。采用电动机检测模块Machines Measurement Demux实时检测电机定子和转子的转速、转矩和三相电流。电机的负载转矩采用阶跃信号模块TL。对于变压器二次侧电压和电流、晶闸管逆变器直流侧电压ud2和电抗器L的电流id、二极管整流器模块Diode的输出电压ud1和输出电流id,采用多路检测仪Multimeter实时检测。对于仿真模型中交流电源、电机定子侧和变压器二次侧其中一相的有功功率和无功功率的检测采用3个功率测量模块Active & Reactive Power2,便于比较串级调速系统的功率流向。

图2　双闭环控制的串级调速系统Simulink仿真模型图

在控制电路部分,由ASR和ACR构成双闭环结构,两个调节器均采用PI控制器。对于外环ASR来说,自电机检测模块引出转速反馈；对于ACR来说,自平波电抗器的电流检测信号id引出电流反馈信号。转速信号由阶跃模块un*设定。ACR输出的移相控制信号uct经函数模块Fcn变换为控制角α。由于晶闸管逆变器模块inverter处于逆变状态,变换函数Fcn=(180°-βmin)-6u,其中βmin为最小逆变角,u为模块的输入信号。在此处,将ACR的输出限幅下限值设为0,鉴于变压器二次侧电压含有较多谐波成分,触发器6-pulse的同步信号取自三相电源。

2.2仿真参数

对于图2所示的双闭环控制的串级调速系统Simulink仿真模型,主要仿真参数如下:

三相电源:Peak amplitude:220*sqrt(2),Frequency为50 Hz；

异步电机:Pn=40 kVA,Vn=380 V,Fn=50 Hz,Rs=0.096 Ω,Lls=0.86 mH,Rr=0.058 Ω,Llr=0.86 mH,Lm=0.031 mH,J=0.4,F=0,P=2

电感:L=10 mH

三相变压器:Pn=40 kVA,Fn=50 Hz,V1=380 V,R1=0.002 pu,Ll1=0.08 pu,V2=350 V,R2=0.002 pu,Ll2=0.08 pu,Rm=5×105pu,Lm=5×105pu,

负载:Step time:1,Final value:300

转速给定:Step time:2,Initial value:10,Final value:7,Sample time:0

ASR:kp=17.42,ki=11.494,积分限幅为:Iup=15,Ilow=-15,PI限幅为:PIup=10, PIlow=-10

ACR:Kp=4.17,ki=41.67,积分限幅为:Iup=15,Ilow=-15,PI限幅为:PIup=10, PIlow=0

移相函数:Fcn=150-6u,u为模块输入,该函数将ACR输出的移相控制信号uct变换为控制角alpha(以角度为单位)。

电流反馈系:0.05

转速反馈系数:0.00667

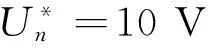
3　仿真结果与分析

图3给出了异步电机双闭环控制的串级调速系统在启动、突加负载和改变电压给定值等调速过程中的转速、转矩、电枢电流、相电流、控制电压和控制角的瞬时响应仿真波形。

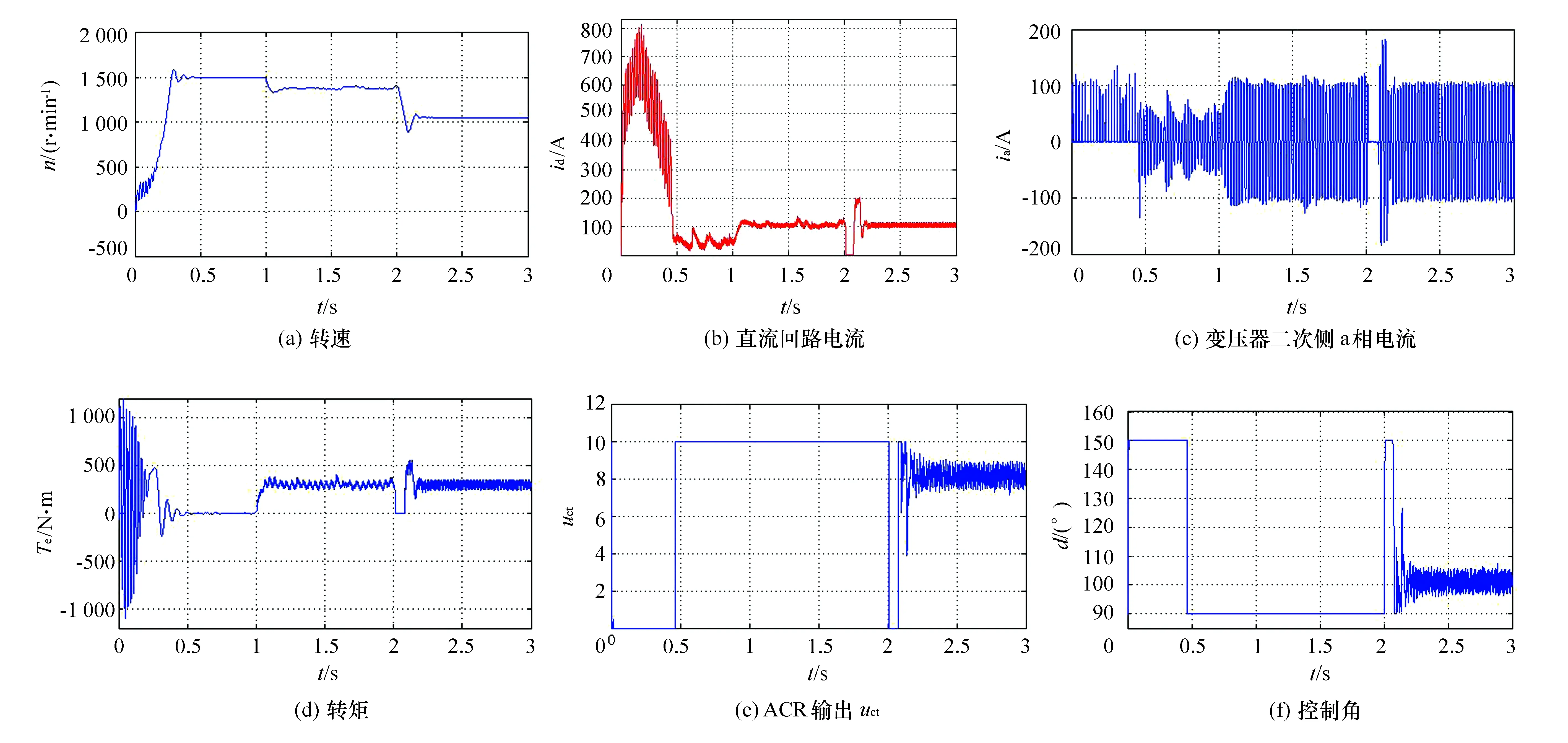
图3　异步电机双闭环串级调速系统部分仿真波形

异步电机双闭环控制的串级调速系统在直接启动时,由于系统的转差非常大,转子的电压特别高,尽管晶闸管整流器的控制角此时已经为150°,βmin=30°,但是直流回路中的电流仍非常大,最大为800 A左右,0.5 s以后,异步电机启动过程趋于结束,转速基本达到额定转速1 500 r/min,此时电流开始迅速下降为零,即理想空载状态,转矩也保持为0,控制角减小为90°左右。由于采用双闭环PI调节器,稳速后系统的控制电压uct保持恒定值10 V不变。从这一点来说,异步电机双闭环串级调速系统在启动时最好用转子串电阻启动,可以有效限制系统的启动电流,待启动过程结束后,再将串级调速装置切换进来。

在1 s时异步电机双闭环串级调速系统突加负载300 N•m,此时异步电机转速下降,直流回路的电流相应上升,转矩也由0上升为300 N•m,系统的控制电压uct仍保持恒定值10不变,经闭环调节后,异步电机进入稳定工作阶段,转速略低于1 400 r/min。

在2 s时,将转速给定值un*由10减小为7,理论上转速由1 500 r/min减为1 050 r/min,从仿真波形图3上看,随着转速给定值的减小,转速迅速随之减小,异步电机进入调速阶段,实测稳定转速为1 050r/min,与理论计算值吻合。

在突加负载、突减转速给定值的调节过程中,由于负载的大小恒定为300 N•m,因此异步电机的电流也不发生变化,随着转速给定值的改变,控制电压uct有所下降,晶闸管整流器的控制角变化为100°左右。

图4给出了异步电机、电源和变压器二次侧各一相的无功功率Q和有功功率P。在1 s突加负载时,电源输出的有功和无功功率、电机输入的有功功率和无功功率均为正值,但是变压器二次侧的有功功率却为负值,这说明异步电机转子的转差功率经串级调速系统输出,并经变压器对电网进行回馈。这也就是串级调速系统能够节能的主要原因所在,但是,从图4(c)可以看出,转子在输出有功功率的同时也产生了较大的无功功率,这会使电源输出的无功功率(图4(a))大于电动机输入的无功功率(图4(b)),会使异步电机双闭环串级调速系统的功率因数下降,这是串级调速系统的不足之处。

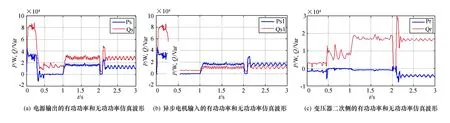
图4　异步电机双闭环串级调速系统的功率仿真曲线

从图5可以看出电动机、电源和变压器二次侧一相的电压和电流的关系,即电流滞后于电压,异步电机双闭环串级调速系统会产生感性无功功率。在图5(c)中可以看到变压器二次侧电流落后于电压超过90°,并因此产生负的有功功率。

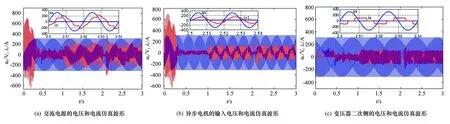
图5　串级调速系统功率、电压和电流部分仿真波形

图6给出了二极管整流器和晶闸管逆变器直流侧电压的仿真波形对比图。从图6(a)可以看出,由于晶闸管逆变器工作于逆变状态,晶闸管逆变器直流侧电压ud2的波形实际是由三相电压的负半周部分波形组成；又因为变压器绕组漏抗等原因,逆变器中的晶闸管产生重叠换相现象,使直流侧电压ud2产生了换相压降,而且在变压器二次侧三相电压波形上形成对应的波形缺口,也会使变压器二次侧三相电压含有谐波。这也会进一步降低双闭环串级调速系统的功率因数。从图6(b)可以看出,二极管整流器的直流侧输出电压ud1和晶闸管逆变器直流侧电压ud2的极性是相反的,因此在实验时需要注意这两个整流逆变模块的连接方式。

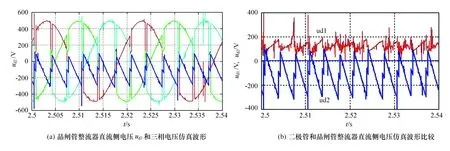
图6　双闭环串级调速系统电压仿真波形比较图

4　结论

通过对绕线式异步电机双闭环控制的串级调速系统的建模与仿真,验证了所建立的Simulink仿真模型的正确性。虚拟仿真结果表明:所建立的绕线式异步电机双闭环串级调速仿真模型的动态响应与实际调速系统的运动过程基本上是相吻合的,仿真结果能够比较准确地反映串级调速系统的实际工作状况。在教学中利用Simulink进行仿真实验,可以比较容易、准确地获取仿真波形,让学生观察到系统在不同控制参数下的输出响应,从而帮助学生加深对系统动态调节过程的理解和建立系统级控制的思想。

References)

[1] 魏伟.基于SIMULINK异步电机矢量控制仿真实验研究[J].实验技术与管理,2009,26(1):71-73,77.

[2] 甄亚,王兵树,殷利杰.斩波串级调速系统功率因数的分析[J].电机与控制应用,2009,36(2):25-29.

[3] 陈伯时.电力拖动自动控制系统:运动控制系统[M].3版.北京:机械工业出版社,2003.[4] 谢胜利.串级调速系统谐波与功率因数的仿真研究[D].保定:华北电力大学,2007.

[5] 顾学雍.联结理论与实践的CDIO:清华大学创新性工程教育的探索[J].高等工程教育研究,2009(1):11-23.

[6] 冯阳,王奔,王亚芳,等.电流型PWM变流器在串级调速中的应用[J].电测与仪表,2014(19):116-122.

[7] 卢秉娟.运动控制系统课程教学突出工程实际应用性研究[J].洛阳理工学院学报:自然科学版,2011,21(3):88-90.

[8] 洪乃刚.电力电子、电机控制系统的建模与仿真[M].北京:机械工业出版社,2012.

[9] 顾春雷,陈中.电力拖动自动控制系统与MATLAB仿真[M].北京:清华大学出版社,2011.

[10] 安跃军,孟昭军.电机系统及其计算机仿真[M].北京:机械工业出版社,2014.

[11] 洪乃刚.电力电子电机控制系统仿真技术[M].北京:机械工业出版社,2013.

[12] 沈艳霞,赵芝璞,纪志成.Matlab/Simulink在运动控制系统教学中的应用[J].贵州大学学报:自然科学版,2005,11(4):435-438.

[13] 孟瑜,刘文辉,张海涛,等.6kV/1250kW绕线式电机的新型串级调速装置[J].电力电子技术,2004,38(1):60-62,74.

[14] 张照彦,马永光,王兴武,等.斩波串级调速系统逆变侧电子保护电路的研究与设计[J].电力系统保护与控制,2015,43(15):1-6.

Virtual experiment and analysis of wound-rotor asynchronous motor cascade speed control system based on Simulink

Zhang Housheng, Yu Lanlan, Meng Tianxing, Jiang Jishun

(College of Electrical & Electronic Engineering, Shandong University of Technology, Zibo 255049, China)

The Matlab/Simulink software is presented into the course’s virtual experiment teaching. The simulation model of wound-rotor asynchronous motor cascade speed control system controlled by dual-loop is established. Simultaneously, the simulation parameters of the proposed simulation model are given respectively. The starting process, the loading process, and the speed dynamically adjusting process when the voltage given value changes, are analyzed in detail based on the simulation results. The feasibility of the cascade speed control system is verified by the simulation results. In the experiment teaching, the Simulink simulation model will help students understand the dynamic adjustment process, establish the system-level control idea. It can also be used for research and development on wound-rotor asynchronous motor cascade speed control system.

asynchronous motor; cascade speed control; simulation model; Simulink

DOI:10.16791/j.cnki.sjg.2016.06.029

2015-10-29

教育部、财政部职业院校教师素质提高计划资助项目(VTNE019)；山东省高等学校科技计划资助项目(J11LG25)；山东省自然科学基金资助项目(ZR2014EL032);山东理工大学青年教师发展支持计划资助项目(L2015011)；山东理工大学综合课程改革资助项目(114129、115061)

张厚升(1976—),男,山东临沂,博士,副教授,主要研究方向为电气自动化、电力电子与电力传动.

E-mail：zhseda@163.com

TM921

A

1002-4956(2016)6-0112-05