大直径高强钢绞线预应力混凝土梁受力性能研究

王　钧　任靖豪

(东北林业大学土木工程学院,黑龙江 哈尔滨　150040)



大直径高强钢绞线预应力混凝土梁受力性能研究

王钧任靖豪

(东北林业大学土木工程学院,黑龙江 哈尔滨150040)

介绍了大直径高强钢绞线预应力混凝土梁的研究现状，分析了正截面、斜截面和两跨连续梁的受弯性能，并总结了大直径高强钢绞线预应力混凝土梁的结构特性，有利于进一步促进大直径高强钢绞线预应力混凝土梁在工程中的应用。

钢绞线，预应力混凝土梁，正截面，斜截面，连续梁，受弯性能

0　引言

目前，建筑结构正朝着大跨度、大空间、超高层、结构构件截面尺寸不断减小的方向发展，提高建筑工程的综合效益已成为设计者所追求的目标，为能达到这一目标，提高建筑所用材料的强度等级是必不可少的。我国目前建筑用钢强度等级主要以500 MPa级以下的中低强钢筋为主，极限强度标准值可达1 860 MPa，甚至1 960 MPa的高强预应力钢筋所占比重很小。高强预应力钢筋的抗拉强度设计值为目前仍大量应用的HRB335级钢筋的4.7倍，作为主导钢筋的HRB400级钢筋的3.9倍、HRB500级钢筋的3.2倍，已研发成功的HRB600级钢筋的2.7倍。大力推广应用配置大直径高强钢绞线的预应力混凝土构件，不仅能够降低建筑钢材和混凝土的消耗量，而且还能带来巨大的经济效益，有利于建筑的节能减排。

通过预应力技术，可使布置在混凝土结构中的高强预应力筋的强度充分发挥，从而可提高结构构件的承载力，可有效控制结构构件挠度与裂缝。为了使大直径高强钢绞线预应力混凝土在工程建设中得到更广泛的应用，因此需要对大直径高强钢绞线预应力混凝土的结构特性和受力特性进行更多的试验研究和分析。

1　研究现状

美国、日本等国家对配置高强钢筋高强混凝土的预应力结构构件的试验研究与应用比较广泛，Padmarajaiah等对后张法预应力高强混凝土梁的裂缝展开了研究[1]，Nawy等进行了22根后张无粘结预应力高强钢筋混凝土梁的受弯性能研究[2]等；研究结果表明，高强材料提高了构件的开裂荷载以及承载力，并且延缓了裂缝前期的发展，而且裂缝数量也较普通预应力构件少。

国内同济大学、郑州大学等也对配置高强钢筋或高强混凝土的预应力构件开展了相应研究，杜毛毛对配置500 MPa钢筋后张有粘结预应力混凝土梁受弯性能研究[3]，通过研究配置500 MPa级钢筋作为纵向受拉非预应力筋的后张有粘结预应力混凝土梁的受弯性能，研究结果表明，试验梁具有较好的抗裂能力，在达到受弯极限状态时，500 MPa高强钢筋均能屈服，梁的破坏为纵向受拉非预应力筋先屈服，而后受压区混凝土被压碎。于秋波等人将7根配置500 MPa级钢筋作为纵向受拉非预应力筋、钢绞线作为预应力筋的混凝土梁进行了受力性能研究[4]，研究结果表明，采用HRB500级钢筋作为纵向受拉普通钢筋的预应力混凝土梁的受力性能与普通预应力混凝土梁基本相同，高强材料的强度均能充分发挥，而且试验梁临近破坏时，具有很好的延性；蒋庆、叶献国等人设计制作12个配置HRBF500级高强钢筋高强混凝土预应力梁试件，研究了高强钢筋高强混凝土预应力梁的抗裂性能[5]，研究结果表明，高强钢筋高强混凝土构件具有很好的抗裂性能。

国内外研究都表明了[6-9]，高强钢筋或高强混凝土在预应力混凝土构件中其性能得到了充分发挥。而且，相比普通预应力混凝土构件，高强钢筋或高强混凝土预应力构件强度更大，变形更小，材料利用率更高。

2　试验研究

2.1简支梁正截面受弯性能研究

为了研究大直径高强钢绞线预应力混凝土梁的正截面受弯性能，可设计若干根配有大直径高强钢绞线的预应力混凝土简支梁，并从预应力度，混凝土强度等级以及普通钢筋配筋率等参数分析其对简支梁的极限承载力、平均裂缝间距和短期最大裂缝宽度的影响。

GB 50010—2010混凝土结构设计规范(以下简称《规范》)[10]规定正截面承载力计算公式如下：

(1)

(2)

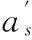
现行规范给出的平均裂缝间距计算公式如下：

(3)

(4)

(5)

其中,cs为最外层受拉钢筋外边缘至受拉区边缘的距离；deq为受拉区钢筋的等效直径；ρte为受拉区钢筋的配筋率；带肋钢筋vi=1.0，先张法预应力钢绞线vi=0.6，后张法预应力钢绞线vi=0.5；As,Ap分别为纵向受拉普通钢筋与预应力钢筋的截面面积。

不考虑长期荷载的影响，现行规范规定的最大裂缝宽度计算公式如下：

(6)

其中，短期裂缝宽度扩大系数τs=1.66；αc为计算截面上混凝土法向预应力等于0时的预加力，此处αc=0.77；ψ为裂缝间受拉区纵向钢筋应变不均匀系数，且0.2≤ψ≤1.0;σs为试验构件受拉区纵向钢筋等效应力。

按照式(1)～式(6)计算出大直径高强钢绞线预应力混凝土梁的极限荷载、平均裂缝间距及短期最大裂缝宽度，与试验实测值进行比较，如果二者吻合较好，说明现行规范规定公式适用于大直径高强钢绞线预应力混凝土简支梁的受弯承载力、平均裂缝间距及短期最大裂缝宽度计算。如果计算值与实测值之比的变异系数较大，则需要按照试验实测值对现行规范规定的计算公式进行适当修正。

2.2简支梁斜截面受剪性能研究

为研究大直径高强钢绞线预应力混凝土梁的斜截面受剪承载力，可设计若干根配有大直径高强钢绞线的预应力混凝土简支梁，并从剪跨比、预应力强度比以及配箍率等因素分析其对简支梁的受剪承载力的影响。

现行《规范》对受弯构件的斜截面受剪承载力应符合下列规定：

V≤Vcs+Vp

(7)

(8)

Vp=0.05Np0

(9)

其中，Vcs为构件斜截面上混凝土与箍筋的受剪承载力；Vp为由预加力所提高的构件受剪承载力；αcv为斜截面混凝土受剪承载力系数，对于一般受弯构件取αcv=0.7；Asv为配置在同一截面内箍筋各肢的截面面积之和；s为沿试件长度方向的箍筋间距；fyv为箍筋实测抗拉强度平均值；Np0为试件计算截面上混凝土法向预应力等于0时的预加力，当Np0>0.3fcA0时，取Np0=0.3fcA0，A0为构件的换算截面面积。

按照式(7)～式(9)计算出试验梁的受剪承载力，与试验实测值进行比较，如果吻合较好，则说明现行规范规定公式适用于大直径高强钢绞线预应力混凝土简支梁的斜截面受剪承载力计算。如果计算值与实测值之比的变异系数较大，则需要按照实测试验数据对现行规范规定公式进行适当修正。

2.3连续梁受弯性能研究

预应力混凝土超静定结构在工程实际中的应用非常广泛，在一定跨度和荷载下，超静定结构相比静定结构的优点有：挠度变形小、刚度大、控制截面的弯矩值小、构件进入塑性变形后其内力会发生重分布，结构的整体受力更为合理。因此研究大直径高强钢绞线预应力混凝土连续梁的受弯性能具有很重要的意义。

设计若干根配有大直径高强钢绞线的预应力混凝土两跨连续梁，通过预应力筋配筋率、非预应力钢筋配筋率、混凝土强度等级等参数的变化，研究大直径高强钢绞线预应力混凝土两跨连续梁的受弯承载力及弯矩重分布规律。

连续梁的弯矩重分布是结构构件在受力过程中当外荷载超过一定值时，构件的某一或若干部位截面表现出非线性行为，截面发生塑性转动，会使结构的弯矩分布不同于原有按弹性结构分析所求的弯矩分布。同样，预应力混凝土连续梁也要发生弯矩重分布，其弯矩重分布的主要影响因素是配筋率以及混凝土的强度等级。

通过对试验所得数据进行理论对比分析，研究主要因素对大直径高强钢绞线预应力混凝土连续梁承载力、破坏形态、挠度以及弯矩重分布规律的影响，并建立大直径高强钢绞线预应力混凝土连续梁的受弯承载力计算公式[11-14]。

3　结语

大直径高强钢绞线预应力混凝土构件，在受力过程中能够充分发挥高强钢筋以及高强混凝土材料的性能，高效利用材料，达到了节能减排的目的。相关研究也表明了，采用高强钢筋或高强混凝土制作的预应力构件，其开裂荷载、屈服荷载以及极限荷载均比一般预应力混凝土构件大。同时，高强预应力筋在高层建筑、大跨度建筑、大型空间结构、高耸构筑物、地下结构以及特种结构的建造中发挥了巨大的作用。大直径高强钢绞线预应力混凝土构件具有以上优点的同时也存在着很多尚待解决的问题：

1)大直径高强钢绞线与混凝土(水泥浆)的粘结强度，及其与不同强度混凝土(水泥浆)粘结应力分布规律。2)预应力混凝土结构中大直径高强钢绞线的应力松弛，着重考察混凝土收缩、徐变对大直径高强钢绞线预应力松弛的影响规律，提出考虑混凝土收缩、徐变影响的大直径高强钢绞线预应力损失的计算方法。3)张拉大直径高强预应力钢绞线，需要专业技术人员以及配套的专用张拉机具和锚具。

[1]Padmarajaiah S K·Ramaswamy A. Crack-width prediction for high-stength concrete fully and partially presrtessed beam specimens containing steel fibers[J].ACI Structural Journal,2001,98(6):852-861.

[2]Nawy E G.Flexural cracking behavior of pretensioned and post-tensioned beams[J].ACI Structural Journal,1985,82(6):890-900.

[3]杜毛毛.配500 MPa钢筋后张有粘结预应力混凝土梁受弯性能研究[D].上海:同济大学,2010:48-59.

[4]于秋波,刘立新,胡丹丹.HRB500级钢筋部分预应力混凝土梁受力性能的试验研究[J].建筑结构,2009,39(S1):527-530.

[5]蒋庆,叶献国,张益民,等.高强钢筋高强混凝土预应力梁抗裂性能试验研究[J].建筑结构,2014,35(12):51-57.

[6]徐风波.HRB500级钢筋混凝土梁正截面受力性能试验及理论研究[D].长沙:湖南大学,2007:83-87.

[7]张利梅,赵顺波,黄承奎.预应力高强混凝土梁抗裂度和裂缝宽度试验研究[J].建筑结构,2004,34(8):45-48.

[8]赵勇,王小锋,苏小翠,等.配置500 MPa钢筋的混凝土梁裂缝试验研究[J].同济大学学报(自然科学版),2011,39(1):29-34.

[9]王钧,邬丹,郑文忠.预应力H型钢混凝土简支梁正截面受力性能试验[J].哈尔滨工业大学学报,2009,41(6):22-27.

[10]GB 50010—2010，混凝土结构设计规范[S].

[11]郑文忠,郑弦,王英.预应力混凝土两跨连续梁中无粘结筋极限应力算法研究[J].建筑结构,2005,35(7):67-71.

[12]陆洲导,谢群,何海.碳纤维布加固钢筋混凝土连续梁受弯性能试验研究[J].建筑结构,2005,35(3):33-35.

[13]余志武,周凌宇,罗小勇.钢—部分预应力混凝土连续组合梁内力重分布研究[J].建筑结构学报,2002,23(6):64-69.

[14]张彦玲,李运生,樊健生.连续组合梁弯矩重分布特征及其随荷载的变化规律[J].中南大学学报(自然科学版),2011,42(2):449-455.

On stressed performance of large-diameter high-strength steel stand wire prestressed concrete beam

Wang JunRen Jinghao

(CollegeofCivilEngineering,NortheastForestryUniversity,Harbin150040,China)

The paper introduces the research status of the large-diameter high-strength steel stand wire prestressed concrete beam, analyzes the bending performances of the positive section, oblique section and two-span continuous beam, and sums up its structural features, so as to enhance its application in projects.

steel strand wire, prestressed concrete beam, positive section, oblique section, continuous beam, bending performance

1009-6825(2016)21-0040-03

2016-05-18

王钧(1967- )，女，博士，博士生导师，教授；任靖豪(1991- )，男，在读硕士

TU378.2

A