溜井放矿量与磨损量计算式的数模

詹森昌

（江西铜业股份有限公司德兴铜矿， 江西德兴市 334224）

溜井放矿量与磨损量计算式的数模

詹森昌

（江西铜业股份有限公司德兴铜矿， 江西德兴市 334224）

摘 要：在溜井放矿过程中，井筒井壁会随着井筒内矿石移动而同时产生磨损，这种磨损缓慢、渐进式连续发生的，均匀的向四周发展扩大。提出了连续式的积分方程，推导出溜井井筒的磨损量与放矿量之间关系的数学模型。用德兴铜矿的相关数据进行了计算，计算结果表明，该数学模型所提供的计算数据与实际井筒磨损情况接近，可为矿山规划、溜井设计与生产管理提供可靠的依据。

关键词：溜井放矿；放矿量；磨损量；数学模型

在溜井放矿过程中，井筒必然产生磨损。若管控不严，措施不当，会引起井筒破坏，影响生产，威胁安全，严重时井筒报废。

研究溜井放矿时的井筒磨损规律，减缓井筒磨损速度，延长服务年限，增加井筒通过矿量，是一个重要的研究课题。本文就溜井放矿时井筒磨损规律进行探讨。

1 溜井放矿时井筒磨损

人们在长期观察中发现，溜井在放矿过程中，井筒的井壁磨损呈现：贮矿段井筒磨损速度较小且均匀，井壁光滑［1］；矿石对井壁的磨损轻微，溜井周边面磨损是均匀的［2］；贮矿段溜井磨损均匀，上下磨损速度非常接近［3］；全溜井的井壁光滑、完整，磨损轻微［4］。

根据以上的观察描述，溜井放矿的井筒磨损规律是：在放矿过程中，贮矿段的溜井井筒是以其中心线为中心，向四周磨损扩大是均匀的、相等的。

2 溜井磨损的计算式

2.1 多项式的计算式

式中，Q为溜井放出矿石量，万t；R为摩擦当量，万t/m2；n为放矿后溜井直径磨损扩大多少个0.1m；D0为溜井井筒初始直径，m。

溜井放矿的井筒磨损量与放矿量之间的关系是一个相互渐进且连续的过程。上述使用多项式的推导过程，采用的是渐进式，但不是连续式。因此，与真实的磨损过程不完全一样，其计算结果是有误差的。但由于磨损间隔的“Δd”值选取了较小的0.1m，故其误差不大，且其计算结果偏小。

2.2积分式的计算式

计算式（1）是建立在溜井直径随着放矿的进行而不断扩（磨）大，但在各种不同直径时，用相应直径的1m高的矿石摩擦井壁（放矿），其井筒直径每扩（磨）大0.1m的摩擦次数是相同的［5］。即溜井井筒每磨损扩大0.1m时的放矿量为：式中，S为当时的井筒断面积，m2；H为用于每次摩擦井筒井壁的矿石高度，1m/次；N为井筒直径磨损扩大0.1m时的摩擦次数，次；γ为松散矿石体量重，t/m3。

（2）式中H·N的乘积是使井筒直径磨损扩大0.1m时所需用的相应直径的矿石高度，单位为m；它是个常数，令其为H1。

当溜井井壁的磨损间隔“Δd（Δr）”不是上述0.1m（0.05m），而是任何一个数时，再用相应井筒直径的1m高的矿石摩擦（放矿）井壁，而其磨损扩大所需的摩擦次数也是相同的［5］。其两者的区别是，任何某一数的“Δd（Δr）”所需的摩擦次数是f次，而不是间隔“Δd”为0.1m的N次。因此，任何某一个“Δd（Δr）”间隔时，井筒每次磨损扩大所需的矿石量q为：

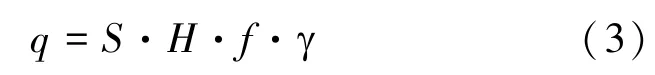
同样，（3）式中H·f乘积是使井筒直径（半径）磨损扩大“Δd（Δr）”时，所需用的相应井筒直的矿石高度，单位为m，令其为Δh。

Δh与H1不同的是：H1=H·N，N是每次井筒磨损大“Δd（Δr）”为0.1（0.05）m时所需的摩擦次数，H1为所需用的矿石高度；Δh=H·f，Δh是每次井筒直径（半径）磨损扩大任何某一数“Δd（Δr）”时，所需的相应井筒直径的矿石高度。Δh是个变数，是随着“Δd（Δr）”的大小而变化；但当“Δd（Δr）”确定为某一值时，Δh随之成为相应的一个定数，即：

溜井的累计放矿量是其直径（半径）每磨损扩大“Δd（Δr）”时所放出的矿石量q之和，即：

式中，V（v）为矿石量Q（q）时的体积，m3。

把（4）式中Δh代入（5）式，得：

当Δr→0，v→0，得：

对（7）式积分：

放矿量为：

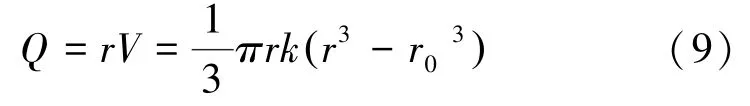
式中，H2为井筒半径为r时的圆锥体高度，m；H0为井筒半径为r0时的圆锥体高度，m。

放矿量Q为：代入（8）式中得：

从（9）式可看出，溜井放矿量与磨损量之间的关系，实质上是一个r为底，H2为高的圆锥体，砍掉其r0为底，H0为高的上部圆锥体，而剩下的下部一个圆台体的关系，如图1所示，这个圆台体是由无数个微小的放矿圆台体组成（见图2）。

图1　放矿圆台体

图2　微小的放矿圆台体

2.3几何形状的计算式

圆台体体积的另一个计算式为：

式中，h=H2-H0，为圆台体的高度，m；其它同前。其放矿量Q：

3 溜井放矿量与磨损量计算式的数学模型

3.1数学模型

从以上的论述可看出，溜井放矿量与井壁磨损量之间的计算式有3个，即（1）式、（9）式和（13）式。

经分析，推荐（9）式为二者关系式的数学模型，即：

从（14）式可看出，r值是随着放出矿石量Q的增加而增大；随摩擦因子K值的增大，r值减小，表明其井筒耐磨，可通过的矿石量增多。

现以德兴铜矿的基础数据（井筒初始直径D0=6m，放出矿石量Q=1018.4万t，井筒直径磨损后为D =7.31m）代入（14）式，其r-Q函数关系如图3所示。

图3　放矿量与磨损量的关系

从图3可看出：当Q值增加时，曲线斜率下降，井筒磨损速度减缓。当井筒井壁岩石坚硬耐磨，或通过井筒的矿石松软时，摩擦因子K值增大，曲线增速减缓，通过溜井的总矿量增加。

3.2数据比较

再次以上述德兴铜矿的基础数据，用上述3个关系式进行计算，具体数字如表1所示。

表1　数据比较表

从表1中的数据可看出，（9）式与（13）式的数据非常接近。一般来讲，二者应该是相同的；但因其参数（h、K）在计算取舍时，造成了误差。（1）式与（9）式的误差，其值在开始时较大，随着放矿量的增加逐步减小，总体来看误差不大。

4 结束语

在溜井放矿过程中，在井筒贮矿条件下，井壁磨损扩大过程，是均匀向四周扩大，并井筒上下的磨损扩大也是相近的。因此，上述3个计算式基本上都能反映这个规律，都可使用。其不同的是：

（1）式是用多项式推导的，存在计算误差，并且计算过程复杂；

（13）式是圆台体的计算式，由于h是个变数，增加计算过程中的复杂性；

（9）式中各变量间的关系清晰，是溜井放矿量与磨损量计算式的圆柱体数学模型表达式，计算方便，其结果也较准确。

参考文献：

［1]邵必林，等.酒钢黑沟铁矿高深溜井正常使用途径的探讨［J］.西安建筑科技大学学报，2002（34）：383-389.

［2]郭宝昆，等.矿石在溜井各区内的移动特点、及其分析［J］.黄金，1985（3）：20-25.

［3]李世广.矿山溜井磨损因素分析及加固措施［J］.矿业工程，2012（1）：64-65.

［4]魏子昌，等.对德兴铜矿1号溜井矿石移动规律及其磨损的考察［J］.金属矿山，1984（8）：7-10.

［5]詹森昌.露天矿山溜井磨损与放矿量的计算式［J］.铜业工程，2015（3）：39-42.

收稿日期：（2016-03-23）

作者简介：詹森昌（1936-），男，教授级高级工程师，主要从事采矿工程相关生产研究工作，Email：214533984@qq.com。