基于响应曲面法的Ar-N2等离子射流特性研究

杨振凯,王海军,刘明,王晶晨,2

(1.装甲兵工程学院装备再制造技术国防科技重点实验室,北京100072;2.河北工业大学材料科学与工程学院,天津300130)

在等离子喷涂中,粉末从等离子射流中获取热能与动能,经加热熔化后,高速撞击到工件表面上形成致密涂层[1]。显然,等离子射流是连接材料粒子和涂层之间的桥梁,好的射流品质是得到高性能涂层的前提和保证。因此,充分了解等离子射流特性,能够避免繁琐的工艺优化过程,并直接利用射流特性制备出高质量的涂层[2]。射流最重要的性质是射流的温度和速度的变化规律,然而超音速等离子喷涂射流速度最高可达3000 m/s,温度可达10000℃[3],目前还缺乏有效的手段对射流温度、速度进行准确测量。刘丹等[4]利用光谱辐射谱线强度法,研究了4种氩氮混合比下等离子射流的温度场分布。高阳等[5]采用焓探针,对小功率(5 kW)等离子体射流的焓、温度和速度进行了测量和计算。这些工作都为等离子射流特性研究和等离子喷涂中次级气的使用提供了参考。响应面优化法(Response Surface Methodology,RSM)是一种高效的试验设计和统计分析的方法[6—7],适于解决非线性数据处理的相关问题,本文采用响应曲面法对射流特性中相关实验进行设计和分析。

影响等离子射流特性因素有很多,诸如电功率(P)、氩气流量(Q)、次级气比例(C)等。电功率是电压和电流的乘积,决定外部输入的总能量;在其他参数相同的情况下,功率越高,喷嘴中的能量密度就越大,在一定范围内离子气的电离就越充分,射流的温度和速度越高,相应射流对粉末的加热加速能力也更大。电压一定时电功率主要受电流影响。另一个显著影响射流特性的工艺参数为等离子喷涂的工作气,具体包括用于引弧并提供初级热焓的主气流量,用于产生电压并提供主要热焓的次级气比例(即占主气的百分比)。电流、主气和次级气比例不同的搭配方式,可以使射流产生不同的特性,从而满足不同粉末的喷涂需求[8]。基于以上对影响射流特性影响因素的基本分析,本文选定电流、主气流量和次级气比例作为输入因子,将射流距喷嘴出口90 mm处的粒子飞行速度及表面温度作为输出响应,设计相关实验研究电流、氩气流量QAr、次级气占主气的比例C(C=QN2/QAr)对等离子射流的影响规律,以期为射流品质研究和喷涂工程实践提供新的参考。

1 实验设计

对北京桑饶公司的AT40粉末进行测温测速,粉末形貌如图1所示,粉末直径为40～50 μm,流动性较好,能够满足超音速等离子喷涂要求。材料粒子的温度、速度能在大功率、大主气梯度范围被 Spray watch捕捉,符合实验要求。喷涂过程采用氩气为主气,N2为次级气,研究Ar-N2等离子射流特性[9]。

采用先进的SprayWatch-2i CCD在线监测系统对超音速等离子射流中的粒子速度、温度及流量分布进行在线监控[3],由此作为反馈来调控和优化喷涂工艺。

采用Design-Expert进行设计,共17组实验,其中X1为喷涂电流、X2为主气流量、X3为次级气比例,具体实验因素及水平选取见表1。

表1 射流特性影响因子及取值水平Tab.1 The influencing factors of the jet characteristics and their numeric values

2 结果与讨论

2.1 响应方程的建立与显著性分析

采用Design-Expert对实验数据进行分析[10—11],分别得到粒子速度、温度和输入因子之间的关系方程式分别为:

对粒子速度的影响因素排序为QAr＞I＞C,对粒子温度的影响因素排序为I＞QAr＞C,三者的影响程度相近且都比较大。粒子速度的2FI预测模型的方差分析见表2,可以看到,模型的F值为8.28,P=0.0021≤0.05,说明因子和自变量之间所建立的回归方程的关系显著;同时,失拟度 F值为5.09,P=0.0686＞0.05,说明不显著。从表中分析还可知,在3个因子中QAr的P值＜0.0001,说明主气流量的大小与粒子速度高度显著,I和C两个因子的P值分别为0.0047和0.0011,与粒子速度影响相关,在交互影响项中I×QAr和QAr×C的P值＜0.05,交互影响关系显著。这也和粒子速度回归方程中的系数分析结果相同[12]。

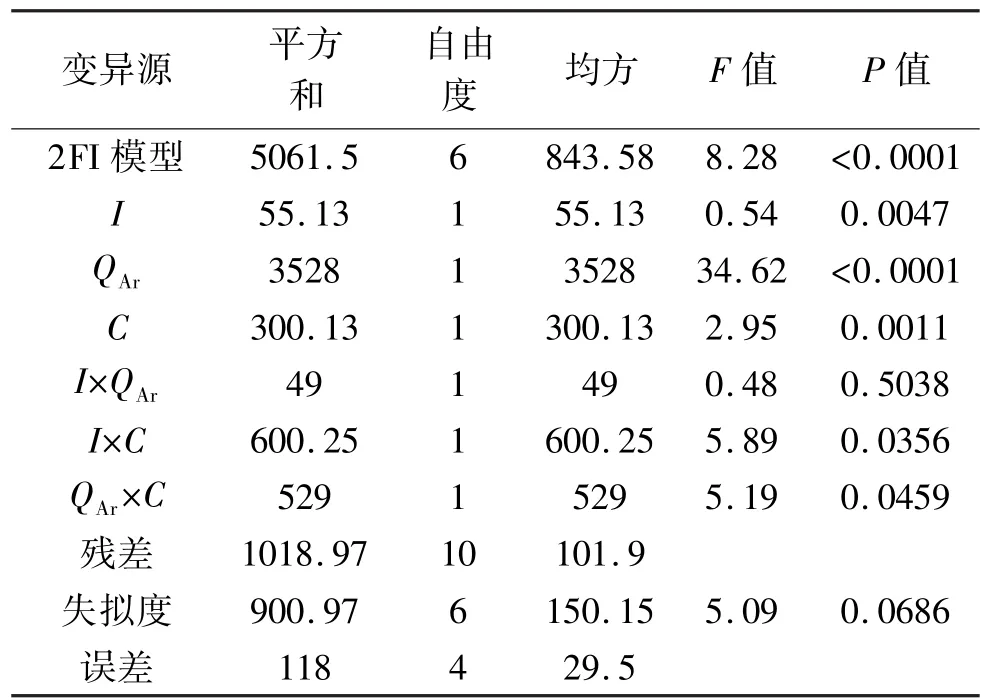
表2 粒子速度的2FI模型方差分析Tab.2 The variance analysis of particle velocity using 2FI regression model

粒子温度的Cubic预测模型的方差分析见表3(采用三次多项式进行拟合的原因是模型的非线性比较强,线性拟合及2FI拟合均不能获得较好的拟合效果),模型的F值为16.27,P值＜0.0001,说明因子和自变量之间所建立的回归方程的关系是高度显著的;在3个因子中I的P值＜0.0001,说明粒子温度的大小与电流I高度显著,QAr和C的P值分别为0.0023和0.0251,与输出响应影响显著,在交互影响项中I×QAr和 QAr×C 以及 I×I和 I×I× C 的 P 值＜0.05,交互影响关系显著。这也和回归方程的系数分析结果相同。响应的内部生化残差分别如图2所示,可以看到,无论是粒子速度还是温度,其模型残差的正态分布都在一条直线上,说明对于粒子速度和温度的模型的预测值和实际值非常接近,综合分析以上数据,说明建立的模型能很好地对粒子速度和温度进行分析预测[13]。

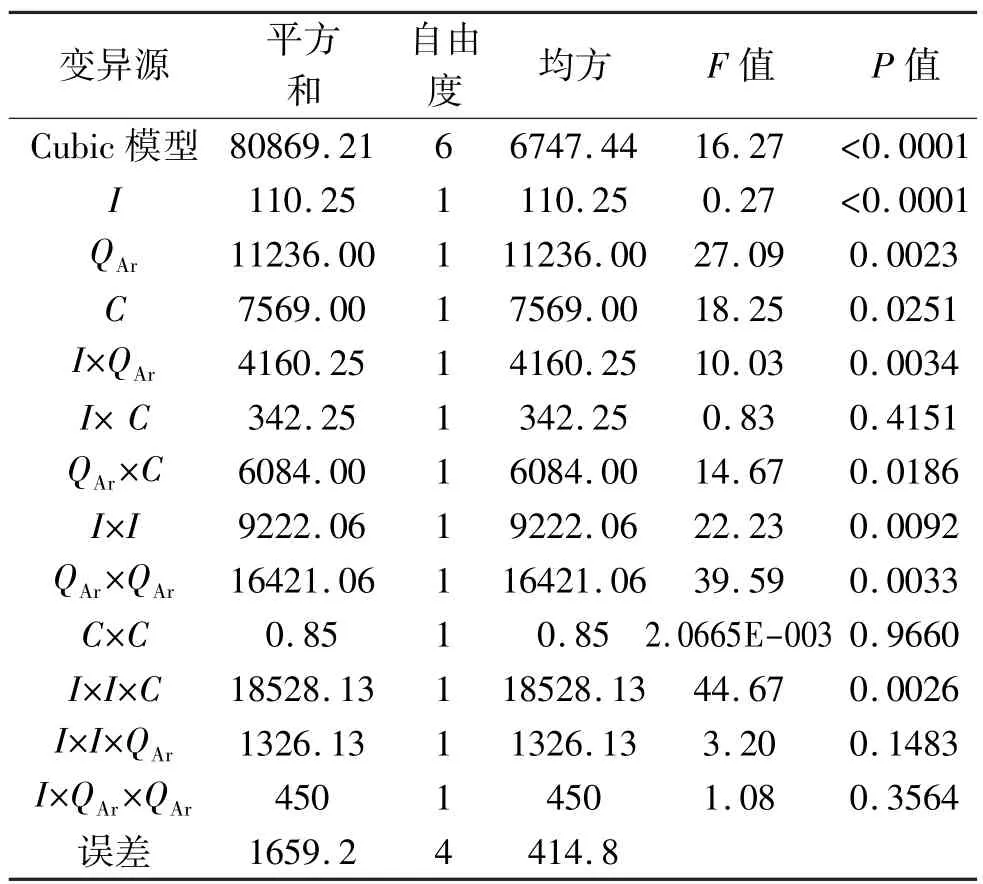
表3 粒子温度的Cubic模型方差分析Tab.3 The variance analysis of particle velocity using Cubic regression model

2.2 射流特性的响应面分析

响应曲面法中的3D曲面图和等高线图能很好地表达出两个因素对于系统响应变量的交互影响情况。

2.2.1 粒子速度的响应面分析

从图3可以看到,当主气流量一定的时候,曲面图呈现三角低一边高的特点,最大的速度在较大电流和大次级气比例下获得。从图4可以看到:当电流为450 A时,小主气和小次级气比例难以获得较高粒子速度,且主气对于速度的影响更大[14]。从图5可以看到,当次级气比例固定,得到最大粒子速度的方式是采用大电流和较大主气。在前面的分析中已经知道对于粒子速度而言,3个因素的排序是I＞QAr＞C,所以重点考察电流和主气对于粒子速度的交互影响。从图5可以看到粒子速度随主气增大而增大,但是当主气增大到130 L/min的时候,粒子速度增加速度放缓,主要原因是在不考虑对射流热焓的前提下,主气流量的增大增加了气体流速,相应对弧柱的压缩作用也增强了,因此射流的刚性增强,但是如果持续不断增大主气流量,则次级气的浓度不断减小,其电离度也会越来越小,从而降低射流的热焓,热压缩效应降低影响了射流速度。在相同的喷嘴条件和电参数条件下,一定范围内主气增大粒子速度增大,但同时也应该看到电流对主气和次级气比例的交互关系,即当电流较大时(如图4),要想获得较大的速度,主气可以在110～160 L/min范围变化,次级气比例也可以较大范围内进行匹配;而当电流较小时(如图5),要想获得较大的粒子速度,图5中最靠近左上角的部分区域,必须在系统最大主气流量下获得,通过大气体流量氩气的气动力效应来给粒子加速。因为电流直接决定了电流密度的大小,当电流密度增大时,弧柱的温度升高,离子气的热电离就更加充分,因此在电流较大,功率较高时候能将离子气充分电离,使得等离子弧能充分压缩,从而提高射流的温度速度[15],而在小电流情形下必须通过加大气流量的方式获得较好的加速。因此,要想获得比较好的加速效应,可以通过合适的主气大小匹配较大的电流和相对较小的次级气比例获得;也可以通过不断增大主气和次级气获得,但是考虑控制喷涂的成本,显然前者的匹配方式更加经济合理[16]。

2.2.2 粒子温度的响应面分析

结合图6可以看到,要想获得较高的粒子温度,可以在I和QAr均较小的时候获得,也可以在较小QAr和较大的I下获得。主气一定时,随着I增加粒子温度上升,随着C上升,粒子温度下降;因为在一定的主气流量下,次级气浓度也有一个阈值,不断加大次级气的比例会使过量的N2冷却射流,从而降低射流热焓。结合图7可以看出,在电流一定时,在QAr=80～140 L/min时,粒子温度均可以和C搭配使得粒子温度达到最大。随着QAr继续增加,粒子温度下降,因为主气的不断加入使射流速度不断加快从而导致粒子的加热时间减少,所以粒子温度开始下降。在对于粒子温度的影响中I＞QAr＞C。从图8可以看到,当次级气比例一定的时候,可以看到在I和QAr较小,而QAr和I较大的时候,粒子温度均能达到最大,约为2450℃,可能的原因是在电流小而主气较大的时候,次级气比例一定,此时次级气的总量非常大,这就为电流小、电流密度不足对于射流温度的影响提供了补偿;当I较大时,电流密度增加,等离子弧弧柱的热压缩效应很剧烈,射流热焓值很高;而当QAr较小,小比例的次级气都被充分电离,因此射流的温度也比较高,从而也能给予粒子足够的加热,粒子温度也能达到最大值。

2.3 实现射流最佳加速、加热效应的工艺参数预测

从牛顿第二定律可知,物体所受合力为其质量与加速度的乘积,即F=ma。因此粒子在等离子射流中所受的射流给予的合力与其速度的关系为:

式中:F是粒子受到的射流给予的合力,当射流速度超过粒子速度时,射流对粒子起加速作用,当射流速度小于粒子速度的时候,射流的合力为阻力,起减速效应;mp是球形粉末粒子的质量;vp是粉末粒子的速度。

式中:rp是粉末粒子的半径,ρp是粉末粒子的密度。轴向飞行的粉末粒子所受的拖动力可用非向量式表示:

式中:ρg为射流的密度,Ap为粉末粒子的截面积,CD为拖动系数,vg为射流的速度,vp为粉末粒子的速度。材料粒子在等离子射流中的速度与等离子射流的速度成正比,相同条件下,等离子射流速度越大,给予材料粒子的拖动力F越大,对粒子的加速效应越强,相应粒子的速度就越大。借助响应曲面法的参数优化和预测功能,分别将响应值粒子速度和粒子温度的优化标准设置为最大,借助拟合出的方程进行求解获得实现最优值的实验参数,得到射流最佳加速效应即粒子速度达到最大时的参数为:主气140 L/min、次级气比例15%、电流400 A。得到射流最佳加热效应即粒子温度达到最大时的参数为:主气80 L/min、电流450 A、次级气比例22.5%。

2.4 模型检验

粒子撞击基体时候的飞行速度以及表面温度直接影响粒子的扁平化和堆垛,对涂层质量具有决定性作用[17]。因此借助响应曲面法对于射流特性的研究,对响应曲面法给出的粒子在喷涂距离处(距离喷嘴出口9 cm)射流实现最佳加速效应的工艺参数进行验证。测得粒子温度为2455℃,速度为578 m/s,与预测值值相比误差分别为0.2%和0.5%,说明所得响应曲面能够较好地模拟粒子速度温度的大小。以最佳加速效应下相关喷涂工艺参数在45#钢基体上制备AT40涂层,具体参数为:主气流量140 L/min,电流400 A,次级气比例15%,喷涂电压144 V,喷涂功率60 kW,喷涂距离9 cm。涂层截面和表面形貌如图9所示,可以看到涂层均匀致密、孔隙少。

3 结论与展望

1)响应曲面法作为一种解决非线性问题的有力工具,有效地避免了单因素法的大实验量,通过得到的二维和三维响应曲面图能直观地看到变量和变量之间的交互作用。

2)利用响应曲面法建立了等离子射流中AT40粒子温度、速度和电流、主气流量及次级气比例之间的二次回归模型。经检验,模型准确,可信度高。

3)影响射流特性最主要的3个核心因素,对粒子速度的影响因素排序为QAr＞I＞C,对粒子温度的影响因素排序为I＞QAr＞C;3个因素对于粒子温度速度的影响具有交互性;在主气140 L/min、电流400 A、次级气比例为15%和主气80 L/min、电流450 A,次级气比例为22.5%的时候,射流分别达到最佳加速效应和最佳加热效应。

4)打破了传统的通过参数优化制备高质量涂层的研究思路,利用粒子温度速度作为指标反映射流特性变化,采用响应曲面法下最佳加速效应对应的离子气及电参数匹配制备,发现涂层均匀致密、孔隙较少,涂层质量高。