桂花树冠层气孔导度模型的优化及其参数分析
罗紫东,关华德,2,章新平,*,刘 娜,张赐成,王 婷
1 湖南师范大学资源与环境科学学院,长沙 410081
2 福林德斯大学环境学院,阿德莱德 5001,澳大利亚
桂花树冠层气孔导度模型的优化及其参数分析
罗紫东1,关华德1,2,章新平1,*,刘娜1,张赐成1,王婷1
1 湖南师范大学资源与环境科学学院,长沙410081
2 福林德斯大学环境学院,阿德莱德 5001,澳大利亚
冠层气孔导度(gc)是许多陆面过程模型中的重要参数,提高对冠层气孔导度的模拟精度非常重要。以环境因子阶乘的Jarvis形式的模型是气孔导度模型中的典型代表,但研究中不同的环境因子有不同的响应方程和参数。研究认为不同的响应方程有不同的模拟效果,并通过比较各环境因子的不同响应方程组合的模型的模拟效果来确定最优的gc模型。以桂花树为例,测定了树干液流、茎水势和微气象环境,用Penman-Monteith(PM)方程反推计算冠层气孔导度并检验不同方程组合的16种模型。模型的参数用DiffeRential Evolution Adaptive Metropolis(DREAM)模型优化。结果表明这种方法能够有效地找到各环境因子最优的响应方程,从而最优化gc模型。优化的gc模型很好地模拟了桂花树冠层气孔导度的变化,尤其是对干旱的响应,模拟值与PM计算值的相关系数和均方根误差分别为0.803和0.000623 m/s。同时也证明了模型中温度函数f(T)>1的现象并非个例,由于温度(T)和水汽压亏缺(D)常是高度相关的,建议在以后的gc模型研究中应把T和D看成一个影响因子,但f(T)>1的这种现象是否具有全球性还有待进一步研究证实。
冠层气孔导度;模型优化;环境因子;树干液流;桂花树
气孔行为是植物生理生态研究中的重要主题,它影响着植物的生长、水分利用和相关生态功能[1]。植被冠层是植被与大气间相互作用的重要界面,调节着生物圈和大气圈间气体、能量的交换。冠层气孔导度是植物响应环境变化的关键参数,同时也是最难估算的参数[2-3]。但在许多气候、水文、陆地生态系统等模型模拟中却是不可忽视的重要参数[4-9]。
冠层气孔导度(gc)可用气孔计测量或用便携式光合作用仪测定的单叶气孔导度推算得到,但所得结果往往变化很大[10],且也难以长期连续观测。随着测定技术的发展,通过树干液流测定整树蒸腾后再利用Penman-Monteith(PM)公式可计算长期连续的gc。PM公式综合考虑了植物生理和微气象因素,已广泛成功运用到温带和热带阔叶森林和针叶林的冠层气孔导度的计算中[3,7,11]。
在过去几十年中,关于冠层气孔导度的观测模拟研究已有很多[2-3,7,12-16]。这些模型大部分都是通过冠层导度与环境变量(太阳辐射(Rs)、温度(T)、水汽压亏缺(D)、土壤水分含量(θ)等)间的函数关系计算的[2,12]。而Jarvis[12]模型是这种方法的典型代表,表达如下:
(1)
式中,gmax是不受环境因子胁迫时的最大气孔导度,f(Rs)、f(T)、f(D)、f(θ)和f(Ca)分别是太阳辐射、大气温度、水汽压亏缺、土壤水分含量和大气二氧化碳浓度对气孔导度影响的胁迫函数,其值均在0—1范围内变化。
但Wang等[17]研究发现,在气孔导度模型中的胁迫函数f(T)>1,明显有悖于模型中胁迫函数变化在0—1之间的理论假设[12,18]。许文滔等[7]用Jarvis模型模拟了华南马占相思的冠层气孔导度,但他也忽略了f(T)的范围问题,观察其模型中温度函数也存在参数Kt<0从而使f(T)>1的现象;齐华等[19]对柑橘叶片气孔导度模型的研究中也存在这种情况。因此,在参考Jarvis模型模拟气孔导度的研究中,人们容易忽视f(T)的范围问题,而f(T)>1是确实存在的现象,但这种现象是否具有普遍性尚不可知。
许多研究根据Jarvis-Stewart(JS)方法[2,12]建立了冠层气孔导度响应环境变量的模型,并已在许多地区的不同森林类型中得到了很好运用[1,16-17]。但一方面,许多气孔导度模型都没有考虑干旱的影响,从而削弱了模拟植被应对水分亏缺的能力[20];另一方面,许多研究在气孔导度模型响应方程的选择上显得很随意,没有说明选择的原因[17]以及是否适合所在的研究区域。因为在不同气候或未来气候变化下,人们还不能确定,模型的经验公式或公式参数是否保持不变。
假设不同的环境变量方程的选择会有不同的模拟效果,选择最佳的方程组合可以提高冠层气孔导度模拟的精度。本文的主要研究目的:(1)通过比较不同的响应方程组合的模拟效果来寻找适合本地气候的桂花树的冠层气孔导度模型;(2)主要分析模型中温度函数方程f(T)及其参数kT,验证f(T)>1的现象在本文研究区域中是否也存在;(3)基于JS方法优化的gc模型能否有效模拟gc对干旱的响应。
1 材料与方法
1.1实验场地概况
实验场地位于湖南省长沙市西郊(112°53′20″E,28°09′46″N,海拔70 m),该区属亚热带季风湿润气候,春暖秋凉,夏热冬冷,雨热同期,四季分明。年均降水量1360mm,主要集中在3—6月,7—8月受副热带高压控制,晴天多,高温出现频率最大,极易发生夏季干旱。实验场地在一片桂花园(1500m2,2003年由农地改造而来),株行距约为3m×3 m,林分密度1040株/hm2,平均年龄为8a,平均树高4 m,平均胸径7.9 cm。
实验观测于2013年4月至10月进行,选择生长良好、具有代表性的桂花树2棵(树龄分别为8年和9年,树高分别为3.8 m和4.1 m,胸径分别为7.6 cm和8.1 cm),进行树干液流和茎水势的长期连续观测。同时2013年夏季发生了严重干旱(7月1至8月18日),是湖南1951年以来夏季降水最少、高温干旱最严重的一年[21],这为研究冠层气孔导度模型对干旱的模拟效果提供了很好的条件。
1.2树干液流的测定
树干液流的测定采用热比率法液流表(SFM1, ICT International Pty Ltd., Australia)每隔30min自动监测记录1次数据。每套传感器探头由3个35mm长的探针组成(一个探针用来释放稳定的热脉冲而其余两个用来测定温度的探针分别安装在它上下各5 mm处)。每棵样树在离地面1.3m处的树干南北两侧各装一套传感器,采用特定规格的钻头垂直于树干打3个深为35mm的小孔,然后分别把3个探针按特定顺序插入小孔。每套传感器和数据记录器用一块12V的太阳能板或一节12V蓄电池供电。最后在仪器外部用铝箔纸包好,以防晒防雨,保持探针周围的环境稳定。
在实验监测结束后,采用生长锥钻取木芯,以获得边材厚度、树皮厚度、边材鲜重和干重以及新鲜边材体积等信息。这些信息都将输入Sap Flow Tool(液流数据的分析和可视化,ICT International Pty Ltd.)[22]分析软件,处理计算液流速率和液流通量,具体方法可参考Burgess等[22]。桂花树的蒸腾(Ec)根据样树对应的有效冠层投影面积和液流通量计算得到。
1.3茎水势的测定
茎水势(ψst)的测定采用热电偶茎干湿度表(PSY, ICT International Pty Ltd., Australia)每隔30min自动监测记录一次数据。这是由Dixon和Tyree[23]研制而近些年被广泛应用的一种植物茎水势监测仪器。PSY茎干湿度表的黄铜腔室内有2个热电偶,一个稍微凸出腔室的热电耦与木质部表面(在所测枝条上用刀片割出一块约2cm2初露木质部的平整表面)接触,用来测量木质部表面的温度,位于腔室内部的热电偶则用来测量腔室内的温度,而茎水势就依据这些所测温度校正计算而得[23]。PSY茎干湿度表固定在枝干后,需在黄铜腔室外围涂上乳胶,再用锡箔纸包好,防雨防晒保持腔室内的环境稳定。同样每套仪器用一块12V的太阳能板或一节12V蓄电池供电。PSY茎干湿度表测定的水势范围为-0.01 至-10 MPa,精度为±0.01 MPa,分辨率为0.002 MPa。
已有研究表明,土壤植物连续体的水势在黎明前可近似达到平衡状态[17,24-25],因此,可用黎明前的茎水势(ψpd)代替土壤水势,反应土壤的水分状态。ψpd用黎明前4:00 —6:00的平均茎水势值来计算。
1.4环境因子的测定
在距实验样地约150m处的开阔地安装微型自动气象站(WeatherHawk-232, USA),每隔30min自动记录环境因子数据。测定项目包括降雨量、太阳辐射(Rs)、空气温度(T)、相对湿度(RH)和风速(U)。其中,空气温度和相对湿度用来计算水汽压亏缺(D)。
1.5冠层气孔导度的计算
PM方程同时考虑了植物生理和微气象因素,是在计算冠层蒸腾方面使用最广泛的方法[26],因此可根据PM方程反推计算冠层气孔导度(gc),其表达方程如下:
(2)
式中,gc是冠层气孔导度(m/s),ga是空气动力学阻力(m/s),λ是水蒸发潜热(J/kg),γ是湿度常数(Pa/℃),Ec是树的蒸腾量(mm/day),ρw和ρa分别是水和空气的密度(kg/m3),Δ是水汽压与气温变化斜率(Pa/℃),Rn是净辐射(J/m2/s),G是地面热通量(J/m2/s),Cp是空气热容量(J/kg/℃),D是水汽压亏缺(Pa),kt和ke是用于单位转换,当Ec为mm/h时,kt=3600 s/h,当Ec为mm/d时,kt=86400 s/d,ke=0.001,用来把Ec从mm/d 转换为 m/d。
1.6gc模型构建
以往的许多气孔导度模型中只关注2—3个环境影响因素[20],综合考虑了4个影响气孔导度的环境因素D、T、Rs和ψpd。(CO2没观测研究,所以未考虑到模型中),参考Jarvis-Stewart的方法[2,12]构建gc模型如下:
(3)
式中,gmax是植物在没有胁迫的理想条件下的气孔导度(m/s),LAI是叶面积指数,函数f(i)是影响气孔导度的环境因子胁迫函数,其值介于0—1之间,这种模型的前提是认为各环境变量是相互独立的。
然而,环境因子的胁迫函数在不同研究中有不同的表达形式,在此,对于每个胁迫函数,本文各采用两种常用的函数,然后通过不同组合构建不同的gc模型,最后通过比较这些模型的模拟效果,得到一个最优的gc模型。具体的函数方程形式见表1。

表1 4个环境因子胁迫函数的不同方程形式Table 1 Different equation forms in stress function of four environmental factors
1.7模型的选择和参数优化
由于降水对液流有影响以及部分时间段降水数据缺失,故本文剔除了降水日的数据,同时,不同样树因个体差异会造成模型参数的较大差异[7]。为了避免这些问题,保证模型及参数的稳定,把两棵桂花树蒸腾及对应环境因子的数据合并成一个数据集(第2棵样树数据追加到第1棵样树数据后面),并按该数据集的自然序列分成两组:Dt奇数组(数据集中的1,3,5,…,等所有奇数序列的数据),Dt偶数组(数据集中的2,4,6,…,等所有偶数序列的数据)。其中,Dt奇数组用来训练gc模型,选出一个最优模型组合,然后用Dt偶数组检验该模型,所有的数据都为日尺度数据。4个环境因子不同方程组合的16种模型见图1。每一个gc模型的参数采用DiffeRential Evolution Adaptive Metropolis(DREAM)模型[33]来计算。DREAM可以根据所给方程自动优化参数[17],为了获得可靠的优化参数让每一个模型在DREAM里都迭代60000次。

图1 4个环境因子不同胁迫方程组合的16种gc模型(右侧M1—M16是对应的模型编号)Fig.1 16 gcmodels combined with different stress functions of four environmental factors, Symbols on the right are the model numbers (M1—M16)

图2 桂花树的日蒸腾量(Ec)及部分环境变量概况Fig.2 Daily transpiration (Ec) of Osmanthus fragrans and part of environmental variables (Rsis solar radiation, T is average air temperature, D is vapor pressure deficit, ψpdis predawn stem water potential and Rainfall); The broken on lines is due to the missing dataRs是太阳辐射,T是日平均温度,D是水汽压亏缺,ψpd是黎明前茎水势,Rainfall是降雨量,图中曲线断开是因为仪器故障导致的数据缺失
2 结果与分析
2.1冠层气孔导度与环境影响因子的关系
本研究以实测树干液流计算桂花树整树的蒸腾量,进而利用PM方程计算冠层气孔导度(gc)。图2展示了2013年观测期间环境条件及桂花树蒸腾随时间的变化,其中7月至8月中旬发生了严重的夏季干旱,高温无雨。日均气温(T)和水汽压亏缺(D)在整个观测期间具有相似的变化趋势。黎明前的茎水势反应了土壤水分状况,在干旱前土壤水分充足,变化不大;干旱持续时土壤越来越干,干旱后才逐渐恢复水分状况(8月10日水势的突然上升是由桂花园主人浇水所致,因此也造成随后的桂花树蒸腾用水的增加)。桂花树的蒸腾(Ec)对降水响应很敏感,易受降水环境的干扰,因此本文在冠层气孔导度模拟时剔除了有降水事件的数据。蒸腾还受其他环境因子的影响,尤其是土壤水分条件,在干旱前蒸腾总体保持较高水平,在干旱期间土壤水分亏缺加剧时随之降低,干旱后随水分条件好转逐渐恢复。
冠层气孔导度与温度、水汽压亏缺、土壤水分状况等关系密切,由图3可看出,gc与D呈显著负相关,尤其当D> 1.75 kPa时,gc显著下降;gc与ψpd呈显著正相关,随ψpd的降低而减小;gc与T的关系较复杂,当日平均温度超过约30℃时,gc下降明显;而gc与Rs虽未呈现正或负相关的关系,但作为gc的能量来源也密切影响着气孔的开闭。由此也看出D和ψpd是影响桂花树gc的两个最主要影响因素。
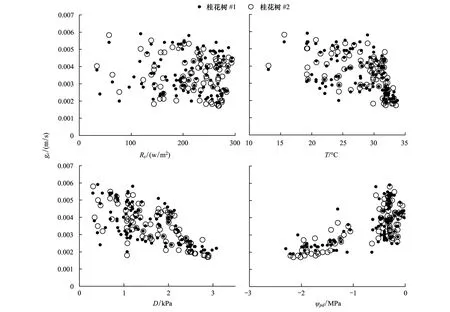
图3 冠层气孔导度(gc)与4个影响因子(Rs、T、D、ψpd)的关系Fig.3 Relationship between canopy stomatal conductance (gc) and four influencing factors (Rs, T, D, ψpd)
2.2模型优化及其验证
为比较16种模型的优劣,选择一种适合桂花树的最优模型,计算了模拟gc与PM计算的gc两者间的相关系数(r)和均方根误差(RMSE),并以此作为模型评价的标准。所有模型中只有M1,M9和M13表现较好,同时具有较高的r和较低的RMSE(图4)。相比之下M9的组合模型是最优的(图4和图5)。当Rs和D的方程一样时,T和ψpd选择f(T)-1和f(ψpd)-1的组合效果明显好于其他用f(T)-2、f(ψpd)-2的方程组合(图4)。例如,在模型1—4中,训练模型中的相关系数分别为0.801,0.807,0.786,0.790,均方根误差分别为0.00062,0.00063,0.00064,0.00067 m/s。在图5可看出,对于温度,所有和f(T)-1的组合都优于和f(T)-2的组合的模型;对于太阳辐射,两种方程组合的模型效果差异不大(图5),r和RMSE都很接近;对于水汽压亏缺,指数形式的方程模拟效果优于线性方程(图5);对于黎明前茎水势,用f(ψpd)-1的方程结果好于f(ψpd)-2的组合模型。
从图4和图5的统计分析可知,M9是本研究中的相对最优模型,分别由4个环境因子胁迫函数中的f(Rs)-2、f(D)-1、f(T)-1和f(ψpd)-1方程组成,最优模型方程如下:
(4)
图6展示了最优模型模拟的gc与PM计算gc的关系,两组数据的相近程度总体上都较好,检验模型中也取得了较高的相关系数(r=0.78)和较低的均方根误差(RMSE=0.00066 m/s)。但gc的模拟在干旱前存在明显的低估现象,这可能与降雨日前后的环境条件(如阴天,本文只剔除了有降雨事件的日数据)有关。而在干旱后存在一定程度的高估现象,干旱期间模拟效果最佳,这说明本文最佳的冠层气孔导度模型能够有效地模拟出干旱条件下的gc及其变化趋势。

图4 不同模型评价比较Fig.4 Comparison of different models evaluation
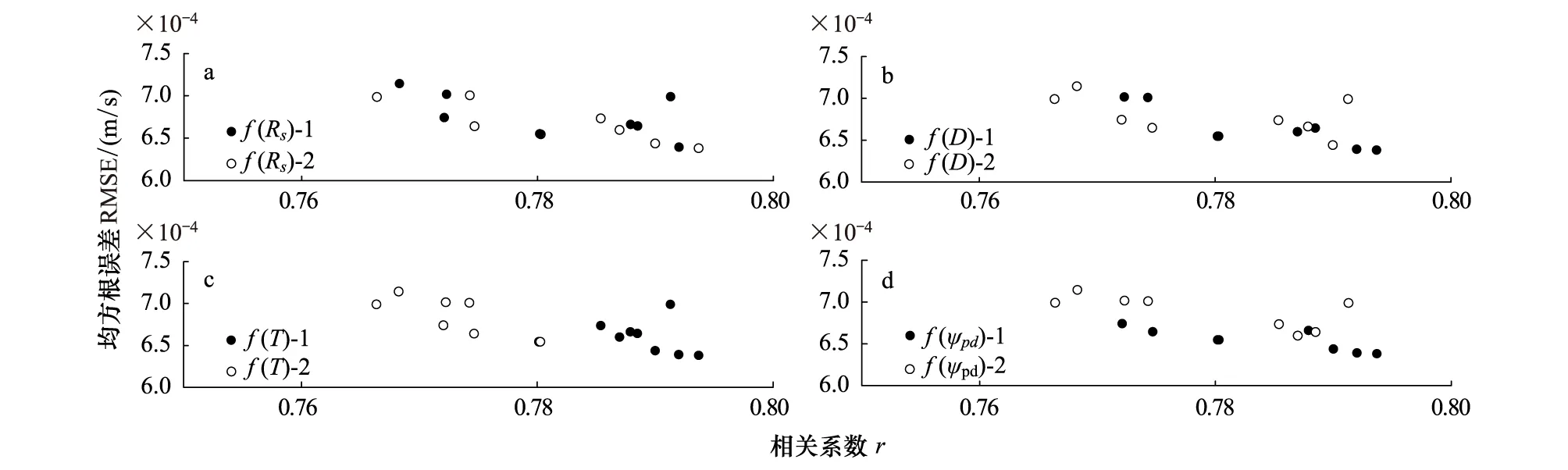
图5 每个环境因子不同响应方程的相关系数(r)和均方根误差(RMSE)Fig.5 The correlation coefficient and root-mean-square error of different response functions for each influencing factor(a)是太阳辐射因子中分别用f(Rs)-1和f(Rs)-2两种方程形式与其他环境因子所有不同方程组合的模型表现,(b)、(c)和(d)也同理,数据为检验模型的数据Dt偶数组
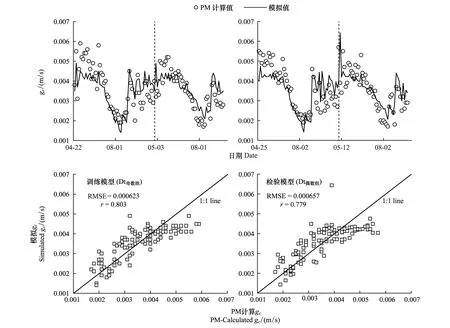
图6 PM方程计算的gc与最优模型模拟gc的比较Fig.6 Comparison of PM-calculated gcand simulated gcfrom the optimized model (M9)
2.3参数分析
Wang等[17]在南澳典型树种DroopingSheoak的冠层气孔导度模拟研究中发现,gc模型中的温度胁迫函数f(T)> 1,参数KT< 0,许文滔[7]和齐华[19]的研究中也存在f(T)> 1现象,这显然与0 ≤f(T)≤1 的原则要求[2]不符。本文主要分析模型中温度胁迫函数f(T)及其参数kT,验证这种现象在本研究中是否也存在。
16种模型中参数kT有正值也有负值,其中正值对应的都是温度函数为线性方程的模型(图7),kT变化范围为[-0.0086,0.0124],这与Wang[17]结论中kT全部为负值略有不同,与许文滔等[7]展示的kT有正值和负值情况类似,但不管是正值或负值都会造成f(T)> 1(图8),这说明gc模型中f(T)> 1的现象不只是个例。为了验证参数kT这种情况是否都存在,把Dt偶数组也放入DREAM参数优化模型中运行,结果kT也是有正值和负值(图7)。其他参数情况具体见表2。
一般函数f(T)的形状是开口向下的抛物线[12,29,34-35]。而本文模型的结果是f(T)> 1,这可能是由于Jarvis形式的gc模型前提是认为各环境影响因子相互独立,实际上各环境因子会相互影响,如D会影响植物水势[36],T和D经常是高度相关的[37],很难区分影响因素各自对气孔导度的影响。而且T和D在整个观测期间都具有相似的变化趋势(图2)且两者显著相关(图8),指数相关系数达0.83,对gc的影响都较明显(图3)。
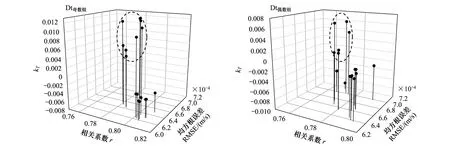
图7 不同模型中参数kT的变化情况Fig.7 Variation of parameter kTin different models虚线椭圆框内都是f(T)-2的模型组合
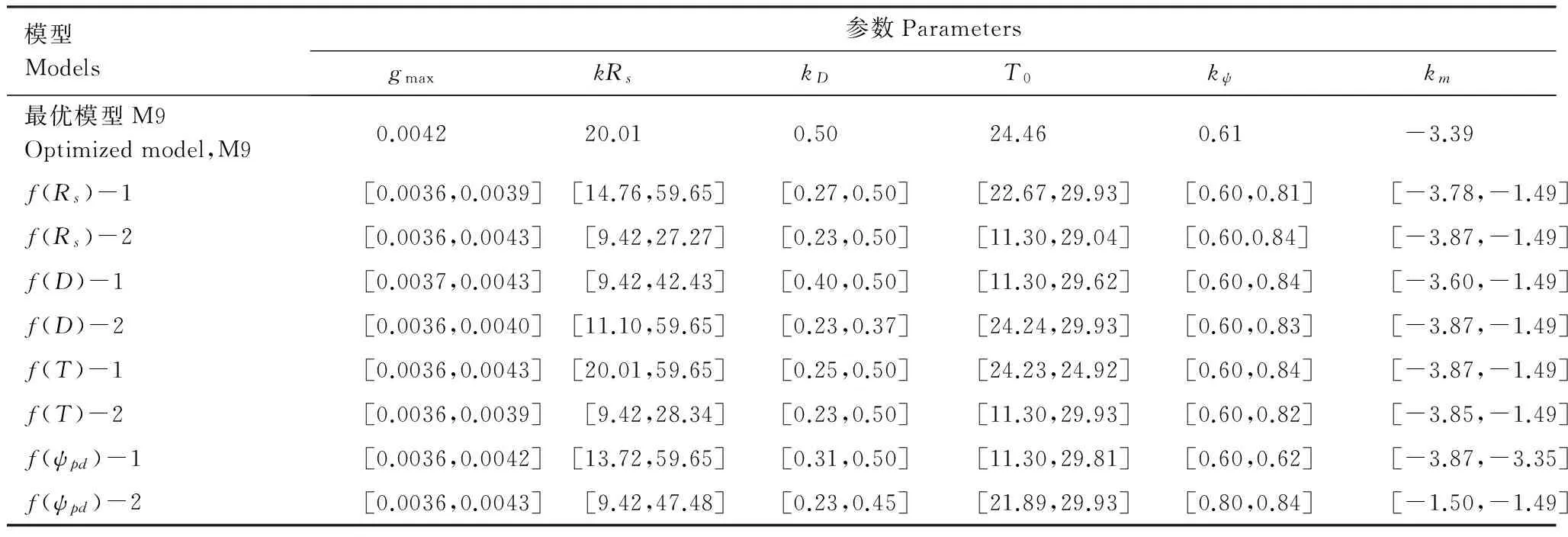
因此,在gc模型中独立考虑f(T)对冠层气孔导度的影响可能会失真,本文引进另一个影响因子f(DT)(图8(b))。当22 图8 温度与水汽压亏缺以及最优模型M9中胁迫函数f(T)、f(D)和的关系Fig.8 Relationship between temperature and vapor pressure deficit and the response functions f(T),f(D), andof the best model M9 模型Models参数ParametersgmaxkRskDT0kψkm最优模型M9Optimizedmodel,M90.004220.010.5024.460.61-3.39f(Rs)-1[0.0036,0.0039][14.76,59.65][0.27,0.50][22.67,29.93][0.60,0.81][-3.78,-1.49]f(Rs)-2[0.0036,0.0043][9.42,27.27][0.23,0.50][11.30,29.04][0.60.0.84][-3.87,-1.49]f(D)-1[0.0037,0.0043][9.42,42.43][0.40,0.50][11.30,29.62][0.60,0.84][-3.60,-1.49]f(D)-2[0.0036,0.0040][11.10,59.65][0.23,0.37][24.24,29.93][0.60,0.83][-3.87,-1.49]f(T)-1[0.0036,0.0043][20.01,59.65][0.25,0.50][24.23,24.92][0.60,0.84][-3.87,-1.49]f(T)-2[0.0036,0.0039][9.42,28.34][0.23,0.50][11.30,29.93][0.60,0.82][-3.85,-1.49]f(ψpd)-1[0.0036,0.0042][13.72,59.65][0.31,0.50][11.30,29.81][0.60,0.62][-3.87,-3.35]f(ψpd)-2[0.0036,0.0043][9.42,47.48][0.23,0.45][21.89,29.93][0.80,0.84][-1.50,-1.49] 气孔导度受环境因素的综合影响,在土壤-植被-大气统一体中发挥着重要的作用。本文通过比较常用的不同环境胁迫方程的组合来优化Jarvis形式的冠层气孔导度模型,找到了适合本区域气候环境下桂花树的冠层气孔导度。 通过比较不同环境胁迫方程的组合来优化gc模型是一种非常有效的模型优化方法。本文得到的优化模型很好地模拟出了桂花树冠层气孔导度的变化,尤其是对干旱的响应。同时也说明胁迫函数方程的选择对gc模型的构造很重要,在未来研究中,这种方法应在更多的不同区域环境、不同森林树种上应用,才能找到适合研究区域不同树种的最佳gc模型。本文研究区域中最优化的桂花树gc模型如公式(4)所示,4个环境影响因子中,水汽压亏缺和黎明前茎水势的最优方程都为指数形式的方程,温度为非线性的抛物线方程,对于太阳辐射而言两种形式的方程效果相当,这点与Wang等[17]的结论相似。这可能是因为气孔导度受太阳辐射胁迫不明显(图3),但深层原因还有待进一步探究。 模型中温度胁迫函数f(T)> 1,这是由T和D高度相关所致,所以在模型构造中应把T和D作为一个影响因子f(DT)看待,结果f(DT)< 1,符合模型要求。同时也证明Wang等[17]提到的温度胁迫函数f(T)> 1和参数KT< 0的现象不仅在地中海气候中存在,在我国亚热带季风性气候区也存在。这种现象是否具有全球性有待进一步的研究和证实。另一方面,本文重点是探索方法,由于样树数量较少,研究具体结果的代表性可能存在不确定性,未来将进行更广泛的研究。 Jarvis-Stewart气孔导度模型前提是各环境影响因子间是相互独立的,当环境因子间存在较高相关时,模型构造时就须谨慎。 [1]Misson L, Panek J A, Goldstein A H. A comparison of three approaches to modeling leaf gas exchange in annually drought-stressed ponderosa pine forests. Tree Physiology, 2004, 24(5): 529-541. [2]Stewart J B. Modelling surface conductance of pine forest.Agricultural and Forest Meteorology, 1988, 43(1): 19-35. [3]Magnani F, Leonardi S, Tognetti R, Grace J, Borghetti M. Modelling the surface conductance of a broad-leaf canopy: effects of partial decoupling from the atmosphere. Plant, Cell & Environment, 1998, 21(8): 867-879. [4]Running S W, Coughlan J C. A general model of forest ecosystem processes for regional applications I. Hydrologic balance, canopy gas exchange and primary production processes. Ecological Modelling, 1988, 42(2): 125-154. [5]Sellers P J, Meeson B W, Hall F G, Asrar G, Murphy R E, Schiffer R A, Bretherton F P, Dickinson R E, Ellingson R G, Field C B, Huemmrich K F, Justice C O, Melack J M, Roulet N T, Schimel D S, Try P D. Remote sensing of the land surface for studies of global change: Models-algorithms-experiments. Remote Sensing of Environment, 1995, 51(1): 3-26. [6]Luo Y Q, Medlyn B, Hui D F, Ellsworth D, Reynolds J, Katul G. Gross primary productivity in duke forest: modeling synthesis of CO2experiment and eddy-flux data. Ecological Applications, 2001, 11(1): 239-252. [7]许文滔, 赵平, 王权, 饶兴权, 蔡锡安, 曾小平. 基于树干液流测定值的马占相思(Acaciamangium)冠层气孔导度计算及数值模拟. 生态学报, 2007, 27(10): 4122-4131. [8]王笑影, 李丽光, 谢艳兵, 李荣平, 李广霞, 周广胜. 植被-大气相互作用中的气孔导度及其尺度转换. 生态学杂志, 2008, 27(3): 454-459. [9]王媛, 张娜, 于贵瑞. 千烟洲马尾松人工林生态系统的碳循环模拟及模型参数的敏感性分析. 应用生态学报, 2010, 21(7): 1656-1666. [10]Jarvis P G. Scaling processes and problems. Plant, Cell & Environment, 1995, 18(10): 1079-1089. [11]Ewers B E, Oren R. Analyses of assumptions and errors in the calculation of stomatal conductance from sap flux measurements. Tree Physiology, 2000, 20(9): 579-589. [12]Jarvis P G. The interpretation of the variations in leaf water potential and stomatal conductance found in canopies in the field.Philosophical Transactions of the Royal Society of London. Series B, Biological Sciences, 1976, 273(927): 593-610. [13]Wang Y P, Leuning R. A two-leaf model for canopy conductance, photosynthesis and partitioning of available energyI: model description and comparison with a multi-layered model. Agricultural and Forest Meteorology, 1998, 91(1/2): 89-111. [14]Blanken P D, Black T A. The canopy conductance of a boreal aspen forest, Prince Albert National Park, Canada. Hydrological Processes, 2004, 18(9): 1561-1578. [15]Orgaz F, Villalobos F J, Testi L, Fereres E. A model of daily mean canopy conductance for calculating transpiration of olive canopies. Functional Plant Biology, 2007, 34(3): 178-188. [16]孙林, 管伟, 王彦辉, 徐丽宏, 熊伟. 华北落叶松冠层平均气孔导度模拟及其对环境因子的响应. 生态学杂志, 2011, 30(10): 2122-2128. [17]Wang H L, Guan H D, Deng Z J, Simmons C T. Optimization of canopy conductance models from concurrent measurements of sap flow and stem water potential on Drooping Sheoak in South Australia. Water Resources Research, 2014, 50(7): 6154-6167. [18]Wang SS, Yang Y, Trishchenko A P, Barr A G, Black T A, McCaughey H. Modeling the response of canopy stomatal conductance to humidity. Journal of Hydrometeorology, 2009, 10(2): 521-532. [19]齐华, 于贵瑞, 刘允芬, 王建林. 柑橘叶片气孔导度的环境响应模型研究. 中国生态农业学报, 2004, 12(4): 43-48. [20]Damour G, Simonneau T, Cochard H, Urban L. An overview of models of stomatal conductance at the leaf level. Plant, Cell and Environment, 2010, 33(9): 1419-1438. [21]罗伯良, 李易芝. 2013年夏季湖南严重高温干旱及其大气环流异常. 干旱气象, 2014, 32(4): 593-598. [22]Burgess S S O, Adams M A, Turner N C, Beverly C R, Ong C K, Khan A A H, Bleby T M. An improved heat pulse method to measure low and reverse rates of sap flow in woody plants. Tree Physiology, 2001, 21(9): 589-598. [23]Dixon M A, Tyree M T. A new stem hygrometer, corrected for temperaturegradients and calibrated against the pressure bomb. Plant, Cell & Environment, 1984, 7(9): 693-697. [24]Vandegehuchte M W, Guyot A, Hubau M, de Groote S R E, de Baerdemaeker N J F, Hayes M, Welti N, Lovelock C E, Lockington D A, Steppe K. Long-term versus daily stem diameter variation in co-occurring mangrove species: Environmental versus ecophysiological drivers. Agricultural and Forest Meteorology, 2014, 192-193: 51-58. [25]Yang Y T, Guan H D, Hutson J L, Wang H L, Ewenz C, Shang S H, Simmons C T. Examination and parameterization of the root water uptake model from stem water potential and sap flow measurements. Hydrological Processes, 2013, 27(20): 2857-2863. [26]Lu P, Yunusa I A M, Walker R R, Müller W J. Regulation of canopy conductance and transpiration and their modelling in irrigated grapevines. Functional Plant Biology, 2003, 30(6): 689-698. [27]Chen F, Dudhia J. Coupling an advanced land surface-hydrology model with the Penn State-NCAR MM5 modeling system. Part I: Model implementation and sensitivity. Monthly Weather Review, 2001, 129(4): 569-585. [28]Whitley R, Medlyn B, Zeppel M, Macinnis-Ng C, Eamus D. Comparing the Penman-Monteith equation and a modified Jarvis-Stewart model with an artificial neural network to estimate stand-scale transpiration and canopy conductance. Journal of Hydrology, 2009, 373(1/2): 256-266. [29]Noilhan J, Planton S. A simple parameterization of land surface processes for meteorological models. Monthly Weather Review, 1989, 117(3): 536-549. [30]Dickinson R E. Modeling evapotranspiration for three-dimensional global climate models. Climate Processes and Climate Sensitivity, 1984, 29: 58-72. [31]Choudhury B J, Idso S B. An empirical model for stomatal resistance of field-grown wheat. Agricultural and Forest Meteorology, 1985, 36(1): 65-82. [32]Lhomme J P, Elguero E, Chehbouni A, Boulet G. Stomatal control of transpiration: Examination of Monteith′s formulation of canopy resistance. Water Resources Research, 1998, 34(9): 2301-2308. [33]Vrugt J A, terBraak C J F, Diks C G H, Robinson B A, Hyman J M, Higdon D. Accelerating markov chain montecarlo simulation by differential evolution with self-adaptive randomized subspace sampling. International Journal of Nonlinear Sciences and Numerical Simulation, 2009, 10(3): 273-290. [34]Chen F, Mitchell K, Schaake J, Xue Y K, Pan H L, Koren V, Duan Q Y, Ek M, Betts A. Modeling of land surface evaporation by four schemes and comparison with FIFE observations. Journal of Geophysical Research, 1996, 101(D3): 7251-7268. [35]White D A, Beadle C L, Sands P J, Worledge D, Honeysett J L. Quantifying the effect of cumulative water stress on stomatal conductance ofEucalyptusglobulusandEucalyptusnitens: a phenomenological approach. Australian Journal of Plant Physiology, 1999, 26(1): 17-27. [36]Tardieu F, Lafarege T, Simonneau T. Stomatal control by fed or endogenous xylem ABA in sunflower: interpretation of correlations between leaf water potential and stomatal conductance in anisohydric species. Plant, Cell & Environment, 1996, 19(1): 75-84. [37]Alves I, Pereira L S. Modelling surface resistance from climatic variables? Agricultural Water Management, 2000, 42(3): 371-385. Optimization of canopy stomatal conductance models forOsmanthusfragransand analysis of its parameters LUO Zidong1, GUAN Huade1,2, ZHANG Xinping1,*, LIU Na1,ZHANG Cicheng1, WANG Ting1 1CollegeofResourceandEnvironmentScience,HunanNormalUniversity,Changsha410081,China 2SchooloftheEnvironment,FlindersUniversity,Adelaide,SA5001,AUS Canopy stomatal conductance (gc) controls transpiration and photosynthesis processes. Thus, the simulation ofgcand its environmental variation forms a significant component of many land surface models. A Jarvis-type model, which calculatesgcfrom a reference value multiplied by scaling (or response) functions of influencing environmental variables, is a typical representation ofgcin land surface modeling. Influential environmental factors often include solar radiation, vapor pressure deficit, and temperature and soil water conditions. Studies have applied different response functions to each individual environmental factor, often without rigorous evaluation. Thus, there is a need to determine which combination of response functions is most appropriate for a specific vegetation cover. In this study, an optimization model ofgcwas determined forO.fragrans, an evergreen tree species in the southern China,based on field measurements. Sapflow, stem water potential, and microclimatic variables were recorded at anO.fragransplantation site in 2013, where a severe drought occurred in July and August of that same year. Sap flow data were used to calculate transpiration, from whichgcwas estimated from the inversed Penman-Monteith (PM) equation, based on micrometeorological data. Predawn stem water potential data were used to estimate root zone water potential, one of the environmental variables influencinggc. Other environmental variables were available or could be derived from the micrometeorological measurements. A total of sixteengcmodels composed of different response functions were examined. Parameters of each candidate model were optimized using the DiffeRential Evolution Adaptive Metropolis(DREAM)model. DREAM runs multiple different chains simultaneously for global exploration and automatically tunes the scale and orientation of the distribution in randomized subspaces during the search for the optimized parameters. The measurement data points were separated to form two sets of data, one for parameter optimization using DREAM, and the other for model testing. The best model was determined based on the statistics of model testing results. The results indicate that this method is useful in determining the appropriate response function for each environmental factor in order to optimize thegcmodel. ForO.fragrans, an exponential function of vapor pressure deficit and root zone water potential, and a parabolic function of air temperature are the most appropriate response functions, whereas no significant difference is observed between different functions of solar radiation. The optimized model shows a significantly improved estimation of thegcofO.fragrans, especially for the drought period. The correlation coefficient and root-mean-square error based on the model testing result were 0.803 and 0.000623 m/s, respectively. The results also suggest that the temperature stress function can be larger than one, a finding that is inconsistent with the conceptual definition of a stress function. Similar findings have been reported in previous studies. This discrepancy is likely attributed to the fact that air temperature and vapor pressure deficit are often strongly interdependent. Thus, to be conceptually consistent, the function of temperature and that of vapor pressure deficit should be combined into one single stress function. Further studies are required to examine if this result applies to other vegetation types globally. canopy stomatal conductance; model optimizing; environmental factors; sap flow;Osmanthusfragrans 10.5846/stxb201506171230 湖南省百人计划项目(2010004);湖南省重点学科建设项目(2011001);国家自然科学基金项目(41571021);湖南省研究生科研创新项目基金(CX2015B167) 2015-06-17; 2015-09-28 Corresponding author.E-mail: zxp@hunnu.edu.cn 罗紫东,关华德,章新平,刘娜,张赐成,王婷.桂花树冠层气孔导度模型的优化及其参数分析.生态学报,2016,36(13):3995-4005. Luo Z D, Guan H D, Zhang X P, Liu N,Zhang C C, Wang T.Optimization of canopy stomatal conductance models forOsmanthusfragransand analysis of its parameters.Acta Ecologica Sinica,2016,36(13):3995-4005.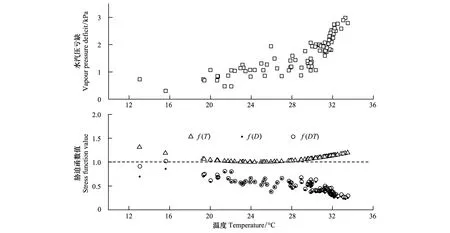
3 结论与讨论

