自动化集装箱码头成组直接中转的岸桥作业调度及其遗传算法*

周秀丹　胡志华

(上海海事大学物流研究中心　上海　201306)



自动化集装箱码头成组直接中转的岸桥作业调度及其遗传算法*

周秀丹胡志华

(上海海事大学物流研究中心上海201306)

针对自动化集装箱码头成组直接中转情况下岸桥的调度问题，以最小化中转完工时间和岸桥的等待时间为目标，建立多目标优化模型，设计多目标遗传算法对模型进行求解.考虑模型中权重等参数的影响，设计3种实验，并对实验结果进行讨论.结果表明,提出的模型具有一定的可行性和实用性，其算法在一定的运算时间内能获得稳定的满意解.

自动化集装箱码头；多目标遗传算法；成组策略；直接中转运输；岸桥作业调度

0　引　　言

针对如何提高码头作业效率和降低码头的运作成本，很多学者从不同的角度对集装箱码头的运作进行了研究.在集装箱场内堆存优化方面，Wu等[1]建立了混合整数规划模型和非混合整数规划模型来解决集成方式下集装箱堆放问题，并对2个模型的结果进行了对比.Fu等[2]对混堆模式的集装箱码头堆场空间资源配置优化问题进行了研究，分别以平衡各箱区贝位间的作业量和最小化泊位到堆场的运输距离为优化目标，建立了两阶段优化模型.Tierney等[3]以最小化集装箱堆放容量和翻箱时间为目标，用启发式算法求解不同堆放原则下集装箱堆存顺序.Carlo等[4]则对集装箱码头堆场使用的设备及堆场的分类方案、发展趋势进行了阐述.毛钧等[5]以平衡各箱区泊位的作业量和最小化集装箱到堆场的运输距离为目标，建立了两阶段模型.其次，由于各项科技的发展，集装箱码头在工艺设计方面也有了极大的突破.孙凯[6]基于船舶大型化这一趋势对集装箱码头前沿操作工艺进行了研究.林浩等[7]对自动化集装箱码头的装卸工艺方案及技术特点进行了全面的分析和对比.最后，在岸桥调度方面，Diaba等[8]分别利用拉格朗日松弛法、遗传算法对岸桥的分配和集成调度模型进行求解.Kaveshgar等[9]利用遗传算法就岸桥的调度问题进了行研究.从以上文献来看，虽然有关集装箱码头堆存方法、新型工艺、岸桥调度方面的研究较多，但研究基于成组中转方式的岸桥调度的文献很少.

成组直接中转方式的特点是岸桥以成组的作业方式对集装箱进行装卸，并且在中转过程中集装箱不进入堆场.即集装箱从一程船(针对某一中转箱而言，将该箱从起始港运至中转港的船舶)上卸下后由二程船(针对某一中转箱而言，将该箱从中转港载运至目的港的船舶)直接运往目的港.鉴于集装箱船上有多个贝位，每个贝位中可能有多组集装箱，每一组集装箱达到的目的港是相同的，便可以考虑岸桥完成同一个集装箱组的所有集装箱装卸作业才开始对下一个组进行装卸，即以成组的方式对集装箱进行作业.成组直接中转的方式不仅有利于二程船上集装箱的有序装载，而且有利于简化一程船上岸桥的调度过程.

文中以自动化集装箱中转码头为背景，针对基于成组直接中转方式的岸桥调度问题，以最小化中转完工时间和岸桥等待时间为目标，建立了多目标混合整数规划模型，设计了多目标遗传算法对模型进行求解，对不同规模的集装箱组的实验结果进行了分析.考虑成组直接中转方式，并针对这一问题从不同的角度进行分析是该文的创新之处.

1　问题描述

自动化集装箱码头中转流程为：一程船到港后，岸桥将集装箱卸载下来，然后由AGV将其运至集装箱堆场；当二程船到港后再由AGV从堆场将集装箱运至二程船岸桥下进行装船.而自动化集装箱直接中转流程主要分为3个过程：(1) 岸桥将集装箱从一程船上卸下；(2) AGV将集装箱运至二程船岸桥下；(3) 岸桥将集装箱装载到二程船上，具体过程见图1.在该流程中，将最后完成集装箱组装载任务的时间称为中转完工时间，将每个岸桥在装卸完一个集装箱组后对下一个集装箱组进行作业之间的时间间隔之和称为岸桥的等待时间.

集装箱直接中转从某种角度上可以简化中转流程，缩短中转时间，对于堆场资源紧张的码头来说意义重大.由于在集装箱直接中转作业中装船和卸船过程基本是同步进行的，这就需要更多地考虑到多条船之间的同步性，因此，集装箱直接中转码头的作业对一程船(从起运港发出的船)和二程船(目的港船舶)到港的时间有了更加严格的要求；同时，集装箱直接中转码头通常要求整个作业完工时间可以达到最小，这就容易出现岸桥在未完成对当前集装箱组的作业，而另一组集装箱已在等待其对它进行作业的情况，使得AGV在岸桥下停留，引起路面拥堵.对此，在中转过程中需要对集装箱组开始装卸时间进行(即岸桥开始对每个集装箱组开始作业的时间)合理的规划，在避免拥堵的情况下求得最小的中转完工时间.

图1　自动化集装箱码头成组直接中转的岸桥作业调度过程

2　模　　型

2.1集合与参数

N为集装箱组集合；Q为岸桥集合；QUuload为负责将集装箱组从一程船上卸下的岸桥集合；QLoad为负责将集装箱组装载到二程船上的岸桥集合；Um为通过岸桥m卸载的集装箱组集合，m∈QUnload；Ln为通过岸桥n装载的集装箱组集合为，n∈QLoad；Tm,n为集装箱组从岸桥m运往岸桥n的时间；TUnload为岸桥卸载一个集装箱的时间；TLoad为岸桥装载一个集装箱的时间；Ai为第i个集装箱组中集装箱的数量；M为足够大的正数，至少大于整个中转完工时间的最小值；λ1,λ2为权重值，范围为0～1.

2.2决策变量

xi为集装箱组i开始卸载的时间；yi为集装箱组i开始装载的时间；xij为集装箱组j卸载完工之后到下一个集装箱组i开始卸载之间的时间间隔；yij为集装箱组j装载完工之后到装载下一个集装箱组i之间的时间间隔；ui,j∈{0,1}为如果集装箱组i紧接着组j卸载，ui,j为1，否则为0；li,j∈{0,1}为如果集装箱组i紧接着组j装载，li,j为1，否则为0.t为中转任务完成总时间；tw为岸桥的等待时间；Ci,m,n∈{0,1}为如果集装箱组i由岸桥m卸载，岸桥n装载，ci,m,n为1，否则为0.

2.3目标及约束条件

集装箱直接中转要求一程船和二程船在港靠泊的时间尽可能短，集装箱组装卸完工时间从一定程度上代表船的离港时间.文中将同一贝位中的一组集装箱作为一个调度任务(一组连续的卸载操作)，在卸载调度任务的过程中，当有两个任务需同时要求同一台岸桥对其进行装载作业时，由于岸桥每次只能作业一个集装箱，其中一个重载AGV停留在岸桥附近，引起路面的拥堵.针对这些实际情况，模型的目标及约束如下.

minimizef2=λ1t+λ2tw

(1)

(2)

(3)

(4)

(6)

(7)

(8)

(9)

(10)

(11)

(12)

(13)

(14)

(15)

xi≥0,i∈N

(17)

(18)

(19)

目标函数定义为最小化中转完工时间和岸桥的等待时间，见式(1).约束条件通过式(19)定义；式(2)为相邻卸载组i与组j之间的时间约束，其中，Aj·ui,j·TUnload表示组j的卸载时间，组i与组j属于同一卸载岸桥m；式(3)表示组i的开始卸船时间与开始装船时间的关系，Ci,m,n·Tm,n表示集装箱从卸载岸桥m到装载岸桥n的运输时间；式(4)同式(2)，表示相邻装载组i与组j之间的时间约束；式(5)表示从卸载完集装箱组j到开始卸载下一个任务i之间时间间隔等于卸载完集装箱组j到开始卸载集装箱组i之间的时间间隔；式(6)表示从装载完集装箱组j到开始卸载下一个任务i之间时间间隔等于卸载完集装箱组j到开始装载集装箱组i之间的时间间隔；式(7)表示在整个中转过程中岸桥的等待时间之和；式(8～11)表示卸载组i与组j之间的相邻逻辑关系，式(8)表示组i在组j之前完成或组j在组i之前完成，式(9)表示组i必须在另一个任务之后完成(或者与相邻，表示组i为首任务)，式(10)表示组i仅且仅与另一个组相邻，式(11)表示在一个岸桥中，首任务出现且仅出现一次；式(12～15)同理可得，表示装载组i与组j之间的相邻关系；式(16)表示最大完成时间大于每一个集装箱组的最终完成时间；式(17)表示开始时间需大于0；式(18)表示时间间隔大于零；式(19)表示中转完工时间和岸桥的等待时间的权重值之和等于1，并且都大于等于0.

3　遗传算法

3.1染色体编码

在遗传算法中，将岸桥作业调度分为2个子问题：(1)每台岸桥的作业序列；(2)该序列下每一集装箱组开始装卸与完工时间.其中前一个问题可在染色体编码中考虑，而后一个题则会在适应度函数中考虑.文中采用十进制法进行编码，每条染色体代表模型的一个解，图2为一个有12个贝位，2台岸桥调度方案的染色体编码.

图2　染色体编码说明

3.2初始种群和适应度函数

鉴于算法的搜索空间比较大，采用随机生成初始种群的方法，增大初始种群的个体多样性，以尽可能增加遗传算法的全局搜索能力，避免陷入局部最优.在算法运行初期，经常会产生一些适应度超常(如很大)的个体，从而控制选择过程，致使算法收敛于局部最优解.为避免这种早收敛现象的发生，文中采用基于排序的适应度计算，首先计算出种群中每个个体的目标函数值，然后将其按升序排序，目标函数值最小的排第1位，最大的排第N(N为种群规模)位，则第i位置个体的适应度为式(20)即为适应度函数，其有效地控制了超常个体的复制概率，维持了种群多样性.

Fitness(i)=2-2(i-1)/(N-1)

(20)

3.3选择运算

选择运算一般要求适应度较高的个体将有更多的机会遗传到下一代群体中.文中采用轮盘赌选择策略.其具体操作过程是：先计算出群体中所有个体适应度的总和；其次计算出每个个体的相对适应度的大小，它即为每个个体被遗传到下一代群体中的概率；每个概率值组成一个区域，全部概率值之和为1；最后再产生一个0～1之间的随机数，依据该随机数出现在上述哪一个概率区；域内来确定各个个体被选中的次数.

3.4交叉运算

交叉运算是遗传算法中产生新个体的主要操作过程，它以某一概率相互交换某两个个体之间的部分染色体.文中采用多点交叉的方法，其具体操作过程是：(1)先对群体进行随机配对；(2)其次随机设置交叉点位置；(3)最后再相互交换配对染色体之间的部分基因，具体见图3.

图3　交叉算子

3.5变异运算

变异运算是对个体的某一个或某一些基因座上的基因值按某一较小的概率进行改变，它也是产生新个体的一种操作方法.在文中，我们采用基本位变异的方法来进行变异运算，其具体操作过程是：(1) 首先确定出各个个体的基因变异位置；(2) 然后依照某一概率将变异点的原有基因值取反，具体见图4.

图4　变异算子

4　算　　例

4.1实验数据

为了验证模型的正确性和有效性，文中采用某集装箱港口数据进行分析.该集装箱港口的总岸桥数为6个，集装箱组数为15，集装箱组中的集装箱个数、负责卸载及装载每个集装箱组的岸桥、集装箱从卸载岸桥到装载岸桥的运输时间见表1，遗传算法参数见表2.同时，岸桥卸载及装载一个集装箱到AGV上的时间分别时90～60 s.文中模型采用Java13编程求解.

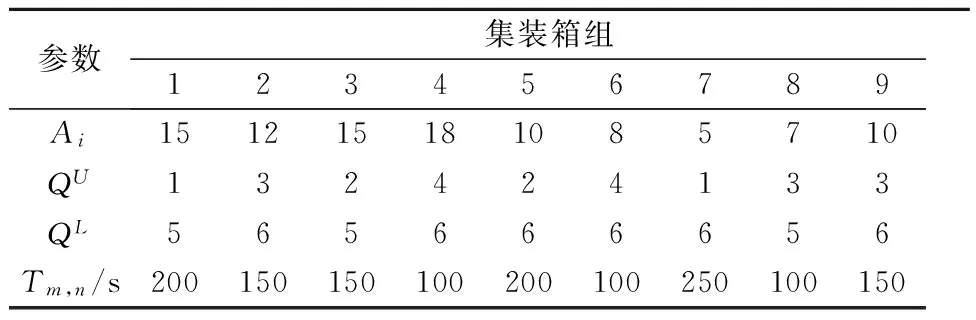
表1　模型参数值

表2　遗传算法参数表

4.2实验设计

设计如表3所列的3个实验.

表3　实验目标、实验场景设置

4.3实验结果及说明

1) 实验1的结果见图5和表4.

根据表1和表2中的数据，在权重值λ1=0.95,λ2=0.05的情况下，算法进化代数和目标值的变化见图5.当算法迭代到154代时，最优值趋于稳定，从而验证了算法具有收敛性、可以行.通过分别用CPLEX和遗传算法对模型进行求解，从表4中可以看出当集装箱的组数分为5，7，9，11，13，15时，2种求解方法得出的目标函数值没有差异，当集装箱组数为17时，通过CPLEX求解的目标函数值稍比遗传算法求解值优.而在计算时间方面，随着集装箱组数的增加，遗传算法的求解速度明显优于CPLEX求解速度.

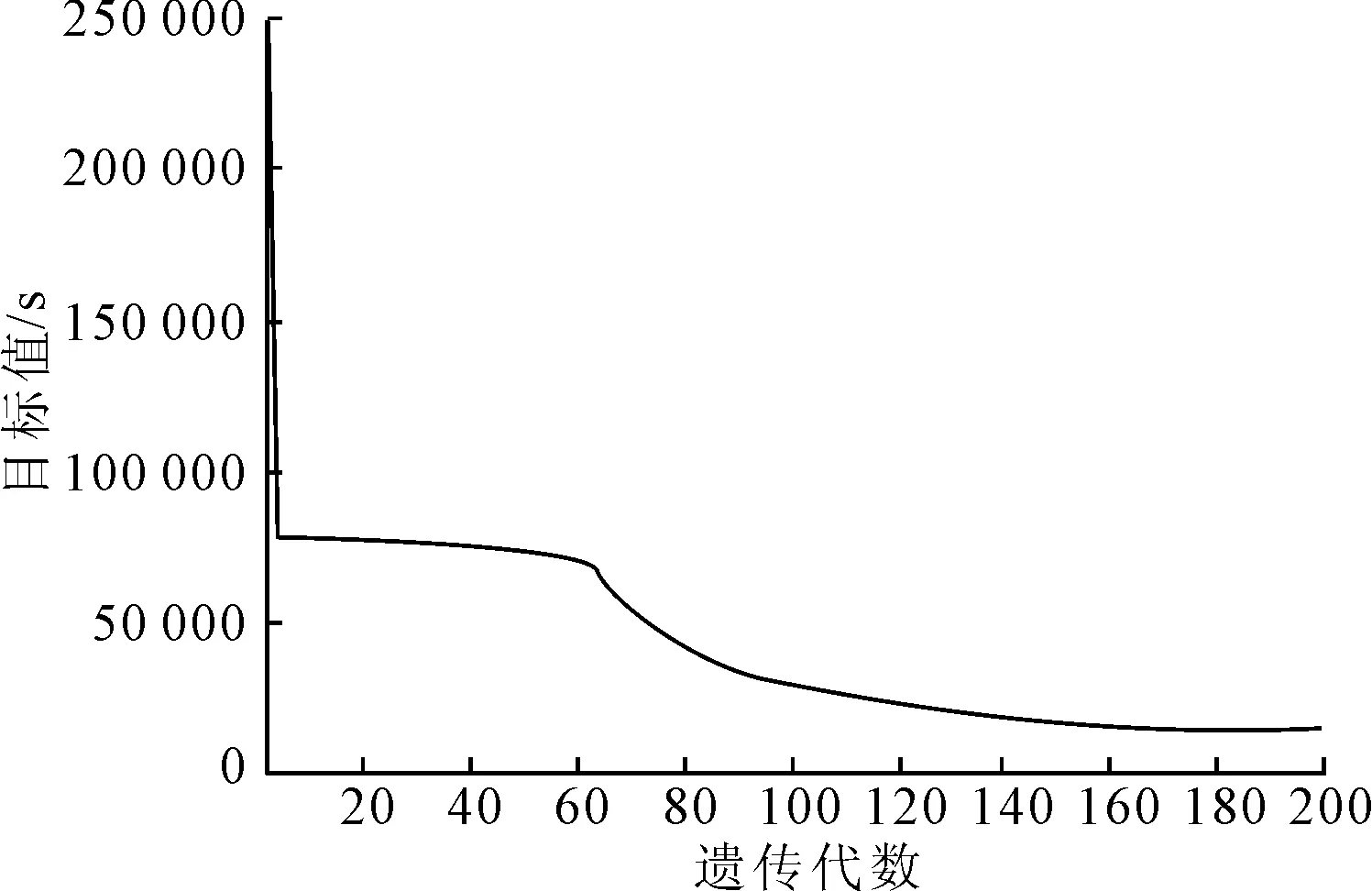
图5　目标函数值随进化代数变化过程

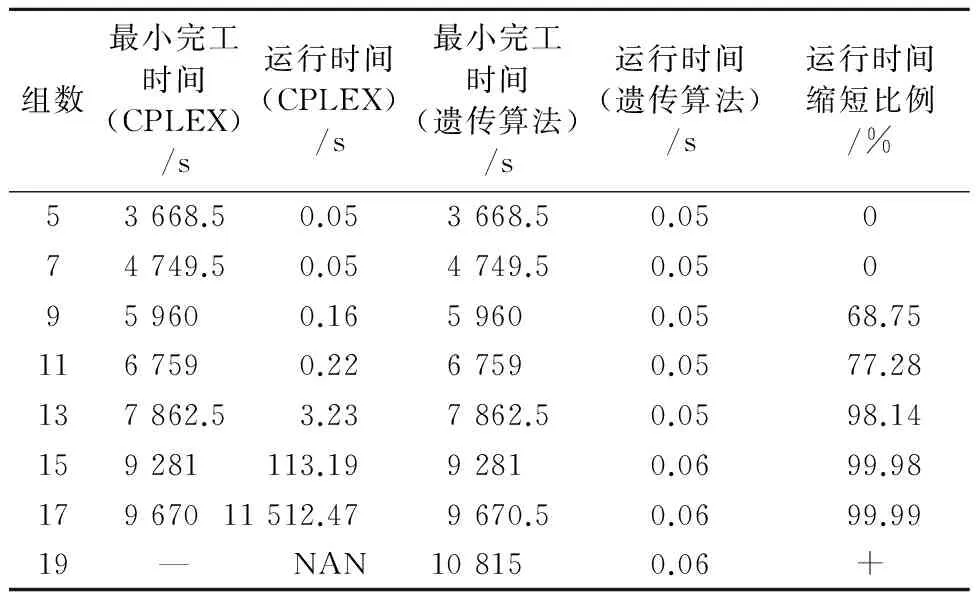
表4　CPLEX和遗传算法求解结果的对比

注：—表示运算内存溢出;+表示无穷大.

2) 实验2的结果见表5及图6～7所示.

根据图6a)，可以看出1～4号岸桥装载集装箱组的顺序依次分别为：8→1→13；5→10→12→6；2→11→15→9；14→7→3→4.5和6号岸桥装载集装箱组的顺序依次为：14→2→11→1→10→4→13→5；8→7→5→3→12→15→9.同样可以看出图6b)中1～4号岸样桥装卸集装箱组的顺序依次分别为：8→1→13；6→12→10→5；11→2→9→15；3→7→14→4.5和6号岸桥装载集装箱组的顺序依：11→6→14→2→4→-10→1→13；3→7→8→12→9→5→15.当集装箱组数为15时，两种权重情况下，求得的完工时间之间的比率为0.971、岸桥等待时间的比率为1.642，可以看出在集装箱组数量为 15时，岸桥等待时间和完工时间之间存在负的相关关系.

表5　开始装卸集装箱组的时间　s

图6　岸桥装作业序列

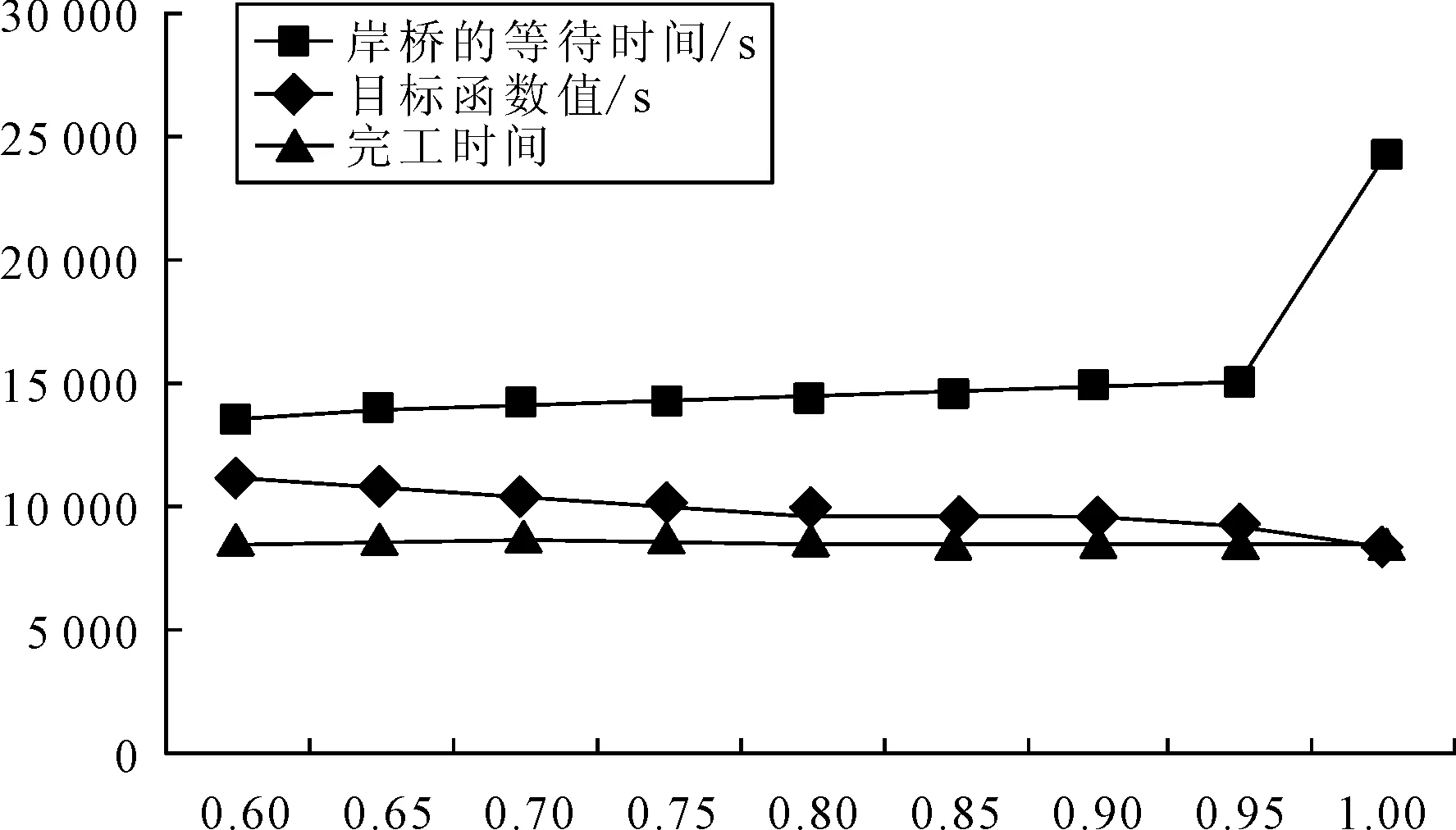
图7　完工时间权重对结果的影响

由图7可知，当只考虑中转完工时间时，中转完工时间最小，岸桥的等待时间最大；当同时考虑中转完工时间和岸桥的等待时间时，中转完工时间权重的增加，岸桥等待时间、目标函数值均呈下降的趋势，而完工时间呈上升的趋势，但上升的趋势很缓慢.

3) 实验3的结果见图8.

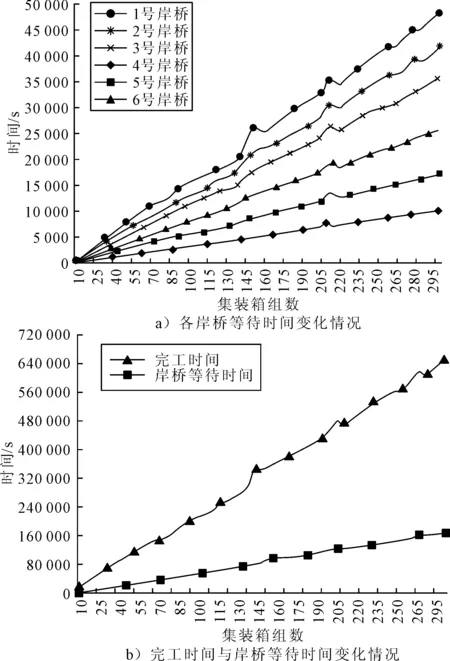
图8　集装箱组数对结果的影响

为了分析集装箱组数对中转完工时间、岸桥的等待时间之间的关系.文中设计了60组数据，在仅增加集装箱组数量的情况，对中转完工时间、岸桥等待时间的关系进行了分析，集装箱组数与完工时间、岸桥等待时间之间的关系见图8.

在装卸集装箱组的岸桥数量不变的情况下，随着集装箱组的增加，最小中转完工时间随之不短增加，且从最小完工时间的变化中可以看出，集装箱组的数量与中转完工时间存在正的相关关系.此外，岸桥的等待时间也随着集装箱组数的增加而增加，但岸桥等待时间增加的速度明显大于中转完工时间的速度.

5　结 束 语

研究自动化集装箱码头直接中转模式下的岸桥调度问题有助于提高码头的作业效率，文中针对自动化集装箱码头直接中转模式建立了岸桥调度的多目标优化模型，考虑AGV运行道路拥堵等因素，以最小化中转完工时间和岸桥等待时间为目标，确定岸桥调度优化方案.设计了多目标遗传算法，借助某码头的数据，运用Java13求解，用实际算例验证了模型的实用性和算法的有效性.经过一系列的实验分析，得到集装箱组数与完工时间、岸桥等待时间之间的关系.集装箱组数越大，完工时间和岸桥的等待时间也越大，完工时间和岸桥的等待时间基本成正的线性关系.同时，中转完工时间和岸桥的等待时间存在悖反关系.在集装箱中转业务不断发展的过程中，如何使得岸桥和AGV更好地协同调度，将是下一步研究的重点.

[1]WU Y, LUO J, ZHANG D, et al. An integrated programming model for storagemanagement and vehicle scheduling at container terminals[J]. Research in Transportation Economics,2013(1):13-27.

[2]FU Y M, DIABAT A, TSAI I T. A multi-vessel quay crane assignment and scheduling problem: formulation and heuristic solution approach[J]. Expert Systems with Applications,2014(15):6959-6965.

[3]TIERNEY K, PACINO D, JENSEN R M. On the complexity of container stowage planning problems[J]. Discrete Applied Mathematics,2014(169):225-230.

[4]CARLO H J, VIS I F A, ROODBERGEN K J. Storage yard operations in container terminals: literature overview, trends, and research directions[J]. European Journal of Operational Research,2014，235:412-430.

[5]毛钧，李娜，靳志宏.基于混堆模式的集装箱码头堆场空间资源配置优化[J].大连海事大学学报,2014(1):117-122.

[6]孙凯.关于集装箱码头前沿操作工艺应对船舶大型化的研究[J].中国远洋航务,2015(1):60-62.

[7]林浩,唐勤华.新型集装箱自动化码头装卸工艺方案探讨[J].水运工程,2011(1):158-163.

[8]DIABAT A, THEODOROU E. An integrated quay crane assignment and scheduling problem[J]. Computers & Industrial Engineering,2014(73):115-123.

[9]KAVESHGAR N, HUYNH N, RAHIMIAN S K. An efficient genetic algorithm for solving the quay crane scheduling problem[J]. Expert Systems with Applications,2012(39):13108-13117.

A Multi-objective Genetic Algorithm for Quay Crane Scheduling Problem Considering Group-based Strategy and Direct Transshipment at Automated Container Terminal

ZHOU XiudanHU Zhihua

(LogisticsResearchCenter,ShanghaiMaritimeUniversity,Shanghai201306,China)

Aiming at the quay crane scheduling problem considering group-based strategy and direct transshipment at automated container terminal, a multi-objective optimization model is established with the bi-objective to minimize the completion time of a vessel and the waiting time of the quay cranes. Then, a multi-objective genetic algorithm is designed to solve the problem. Considering the effects of weights and other parameters of the solutions, three experiments are performed and analyzed. The results shows that the proposed model can have certain feasibility and practicality and the algorithm can obtain a satisfactory solution in a certain time.

automated container terminal; multi-objective genetic algorithm; group-based strategy; direct transshipment; quay crane scheduling

2016-06-18

U693

10.3963/j.issn.2095-3844.2016.04.030

周秀丹(1991- )：女，硕士生，主要研究领域为港口物流

*国家自然科学基金面上项目(71471109)、国家自然科学基金青年项目(71101088)、教育部博士点基金项目(20113121120002)、交通部应用基础研究项目(2015329810260)、上海市教委科研创新项目(14YZ100)、上海市曙光计划项目(13SG48)资助