基于期望跟驰间距的跟驰模型研究

杨龙海　赵　顺　罗　沂

(哈尔滨工业大学交通科学与工程学院　哈尔滨　150006)



基于期望跟驰间距的跟驰模型研究

杨龙海赵顺罗沂

(哈尔滨工业大学交通科学与工程学院哈尔滨150006)

搭载高精度车载GPS设备进行车辆跟驰实验，采集不同速度和交通流状态下的车辆跟驰数据.对车辆跟驰中的速度、车头间距、速度差，以及加速度等参数之间的关系进行了统计分析，构建了基于期望车头间距的跟驰模型.通过参数标定和数值模拟，比较了安全距离模型和期望车头间距模型，结果表明，期望车头间距模型与实测数据的拟合精度更高，且在加速度变化的平顺性，以及车辆减速行为的表现上更符合实际跟驰行为.

期望跟驰间距；跟驰模型；车载GPS数据；安全距离模型

0　引　　言

车辆跟驰理论既是微观交通流理论最基本的仿真模型，也是理解宏观交通流形成的理论基石，而且具有指导交通组织管理、缓解交通拥堵的现实意义.在跟驰模型研究中，车辆被看成分散的、存在相互作用的粒子，在假设没有超车的情况下，通过研究后车跟随前车的动力学过程，进而分析单车道上交通流的演化特征.Reuscheld等[1-4]的研究标志着跟驰理论解析方法研究的开始.Chandler等[5]在通用汽车实验室首次提出了GHR跟驰模型，并使用卷轴钢丝连接的车辆获取的实地跟驰数据对模型进行参数标定和相关分析.Kometani等[6]通过车辆动力学的方法计算出车辆跟驰中的安全距离并以此构建了安全距离模型.Wiedeman[7]在总结前人研究成果的基础上提出了心理-生理模型，这一模型也成为微观仿真软件VISSIM的核心模块.Kikuchi等[8]将GHR模型的相对速度、相对距离和加速度进行了分类，提出了各个参数的隶属度函数，构建了模糊跟驰模型.这些模型在构建之初由于跟驰数据的采集方法还较为落后，大多是从车辆动力学、驾驶人行为特性等理论方面构建了模型.随着调查手段的发展许多学者对这些模型进行了参数标定和检验等[9-10]，但是基于实测数据对模型结构的修正较少.文中采用车载高精度GPS设备进行了实地跟驰数据调查，在跟驰参数数学关系分析的基础上提出了基于期望跟驰间距的跟驰模型，并与Gipps模型进行了对比和评价.

1　跟驰调查及特性分析

1.1跟驰调查

为获取实地跟驰数据，搭载高精度车载GPS设备开展跟驰实验.该方法的优点有：采集数据精度较高，高精度GPS接收机定位精度在2 cm以内，且不随距离和速度的变化而变化；尺寸较小，便于携带，能够安装在实际交通流中的任何类型的车辆上；不会给司机带来额外操作负担，对司机和其他车辆的心理影响也较小.

文中共使用4台小汽车作为试验车辆，每辆车装备有Trimble R8 高精度GPS流动站、GPS手簿、笔记本电脑和高清行车记录仪，在哈工大二校区交通学院设置GPS基站，基站的覆盖半径20 km.GPS设备以10 Hz的频率获取时间、位置等车辆轨迹相关的地理信息，这些信息通过串口和相关的软件实时传输至笔记本电脑，并以文文中档的格式进行存储.行车记录仪记录车辆行驶过程中的视频和音频，用于车辆行驶环境、跟驰车辆先后顺序，以及行驶中其他事件的记录，便于筛除无效数据.流动接收机和单基站定位，在实验的大部分时间内可以达到网络RTK的定位精度，定位信息输出格式用NMEA-0183中规定的GGA输出格式.在调查地点的选择上，为了研究不同的车辆速度，选择了在良好天气条件下哈尔滨市的支路、次干路、主干路及绕城高速等道路进行了超过3 h的跟驰行驶，采集了超过10万条跟驰数据.

1.2跟驰数据分析

通过对实验数据的筛选，得到大量基于时间序列的车辆跟驰数据，根据已有的跟驰行为研究经验，对车辆速度、车头间距、速度差，以及加速度等参数的关系进行了分析.

1.2.1车头间距分析

已有研究表明，车辆的跟驰间距与后车速度具有较强的相关性.为了探究两者之间的数学关系，以跟驰车速度为横坐标，跟驰间距为纵坐标，绘制速度-车头间距散点，见图1.这些数据显示出在一定的跟车速度水平下，车头间距总是在一定的幅度内进行调整，试图保持与跟车速度相适合的车头间距，Michaels等对此进行了研究并将之称为期望车头间距.

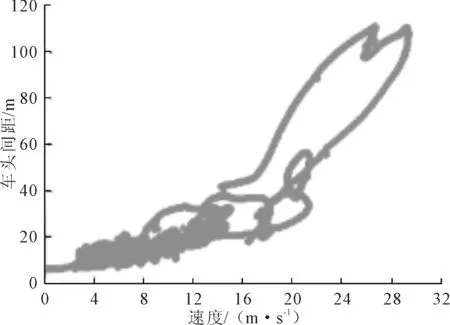
图1　实测速度-车头间距散点图

在以往的研究中，这一期望车头间距的获取往往是对所有的车头间距散点直接进行曲线拟合，得到期望车头间距曲线，然而这样处理存在2个弊端：一方面获取的实地跟驰数据在不同速度下的样本量之间可能存在较大的差异，导致拟合得到的曲线偏向于样本量较大的部分；另一方面跟驰车辆的相对速度、加速度等也会影响跟驰间距.直接拟合不能较好地反应驾驶员对不同影响因素的敏感程度.为了避免样本量不均导致的标定偏差，以及其他相关因素的影响，以速度0.1 m/s为区间宽度，对每个速度区间内的车头间距求平均值，即可得到下不同速度下跟驰中后车期望保持的车头间距，则该速度可以认为是车辆在稳定跟驰状态下期望保持的车头间距(下面简称为期望车头间距)，见图2.

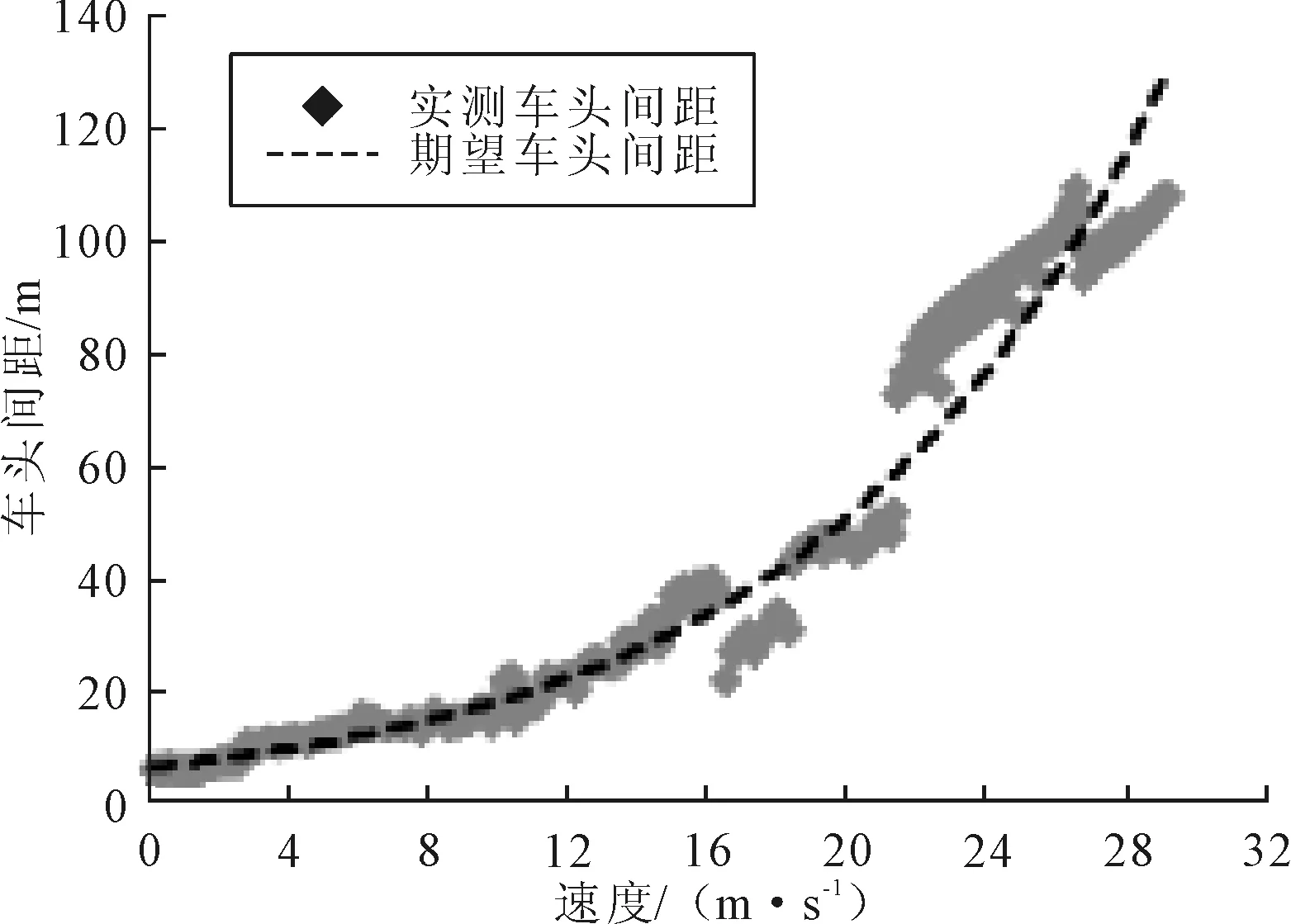
图2　速度-期望跟驰间距关系图

此时对上图中的点数据进行曲线拟合，指数曲线的拟合精度最高，达到0.975，曲线表达式为

(1)式中：xdesire为期望跟驰间距；v为后车速度.以上得到的期望跟驰间距是前后车速度相同的情况下，车辆期望保持的车头间距，然而在实际行驶中，由于前车速度波动及后车驾驶员的判断误差，实际车头间距在一定范围内波动.为了探究这一变化规律，定义实际车头间距与期望车头间距的差为期望间距差，依此为横坐标，以后车的加速度为纵坐标，绘制期望间距差-加速度关系折线图，如图3.

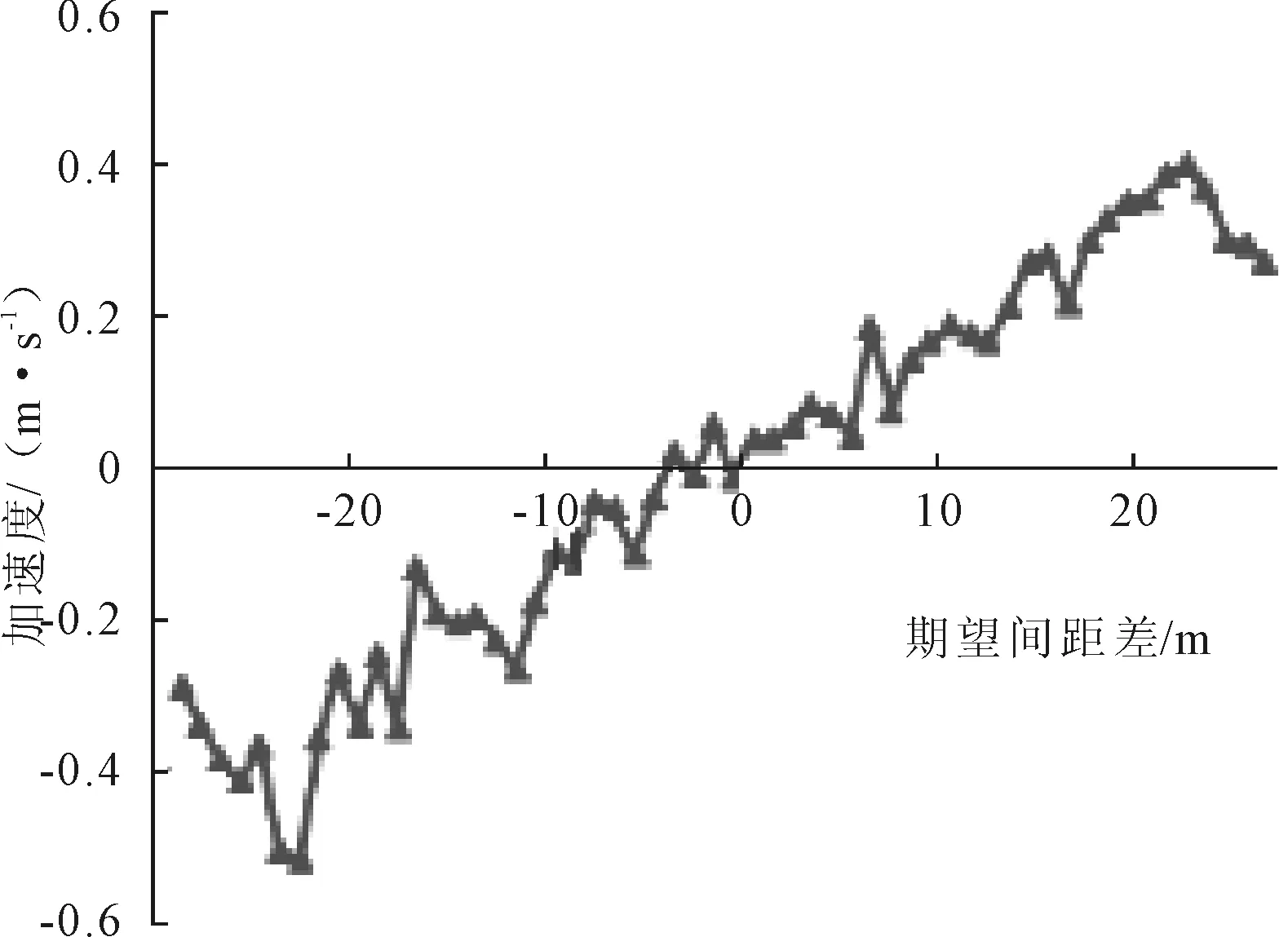
图3　期望间距差-加速度关系图

由图3可知，车辆间距和后车加速度呈现出较为明显的正相关，从跟驰状态的定性分析和驾驶员跟驰特性的研究可以进行以下推断：在稳定跟驰状态，前后车以相同速度保持期望跟驰间距行驶；当前车加速时，前车远离后车，车头间距大于期望跟驰间距，于是后车采取加速措施，速度增大，直到以与前车保持期望跟驰间距行驶；反之，前车减速时，后车接近前车，车头间距小于期望跟驰间距，后车采取减速措施，速度减小，直到与前车相同的速度保持期望跟驰间距行驶或减速停车.

1.2.2速度差分析

现有许多研究将前后车速度差作为影响后车跟驰行为的重要因素，为了探究两者之间的数量关系，类比速度-跟驰间距的数据处理方法，以速度差0.1 m/s为区间宽度，对每个区间内的车辆加速度求平均值，可得到实际不同速度差下后车期望采取的加减速度，见图4.

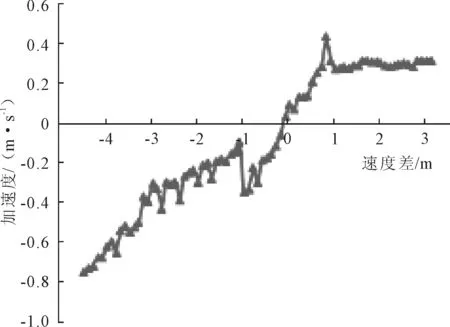
图4　速度差-后车加速度关系图

图4中速度差与后车加速度之间呈现出较为明显的正相关，同时可以发现散点的连线与横轴也就是速度差的交点处速度差为0，即当前后车速度相等时，后车将不再采取加减速行为；当速度差大于0，即前车速度大于后车时，后车将采取加速行为，加速度的大小随着速度差的增加而增加；当速度差小于0，即前车速度小于后车时，后车将采取减速行为，与加速行为类似，期望减速度绝对值随着速度差绝对值的增加而增加，但减速度的增长速度略大于加速度.

2　跟驰模型构建

2.1传统安全距离模型

最早的安全距离跟车模型是由Kometani和Sasaki提出的，其基本假设是驾驶人应在不能完全预判前车运动的情况下，保持合理的安全车头间距以避免碰撞.Gipps提出了另一种目前较为常见的安全距离模型，该模型假定车辆速度由当前理想速度、所允许的最大加/减速度和安全制动距离共同决定，在时间段[t，t+T]内，车辆速度是达到理想速度和维持安全距离的减速度中的较小者[17].Gipps模型的跟驰模块表达式如下.

2.2基于期望间距的跟驰模型

通过对跟驰数据的分析发现，期望间距差和相对速度与跟驰车的加减速之间具有很强的相关性.在Gipps模型的构建中，是车辆动力学计算得到的安全距离为基本公式，通过推导验算计算经过时间间隔T后跟驰车将要采取的行驶速度，没有严格的对加速度进行考虑.但是在实际驾驶中，车辆的加速度是跟驰状态变化的决定因素，应纳入考虑.因此，文中构建的跟驰模型以加速度为因变量，以期望间距差和前后车速度差作为影响后车加减速的直接因素，可以得到下式.

(3)式中：Δxreal为实际跟驰间距；Δxdesire为期望跟驰间距；Δv为前车速度与后车速度之差；m和n分别为车辆对跟驰间距变化和对相对速度的敏感系数，其单位分别为s-2和s-1.当前后车以相同速度并保持期望跟驰间距行驶时，(Δxreal-Δxdesire)和Δv均为0，后车将保持匀速行驶；当前车加速，期望间距差和速度差均大于0，后车将采取加速行为；当前车减速，期望间距差和速度差均小于0，后车将采取减速行为.但是我们注意到，随着车辆跟驰速度的增加，车辆跟驰间距增大，后车驾驶员对于车辆间距以及相对速度的绝对判断能力将有所下降，因此，应该引入期望车头间距以及实际前车速度这两个量，分别作为期望间距差和相对速度的分母，得到基于期望间距的跟驰模型(car-following model based on the expected headway，EH模型)的最终形式为

(4)式中：α和β为驾驶员敏感系数，单位均为m/s2；vl为前车速度；Δvmax为跟驰中前后车出现的速度差的绝对值的最大值.Δvmax的引入是为了避免当前车静止时出现的为0的情况，由本次实地数据标定的值为4 m/s.

3　模型分析

3.1模型的参数标定

在用实测数据进行跟驰模型的参数标定时，通常将其抽象为求解非线性规划最优解的问题，其目标函数即实际数据和模型仿真数据的差值最小，自变量是模型中的各个参数，自变量的约束条件是各个参数有合理的数学和物理意义的范围，形式为

(5)

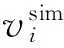
表1　模型参数取值范围及标定结果

为了比较2个模型对实际跟驰行为的拟合程度，对2种模型计算得到的值与实际值进行比较，考虑到模型在参数标定中选取速度的误差作为目标函数，这里以模型计算的期望速度与实际速度的平均误差(ME)、平均绝对误差(MAE)、平均绝对相对误差(MARE)和均方根误差(RMSE)这几个统计变量为指标进行模型的精度比较，见表2.

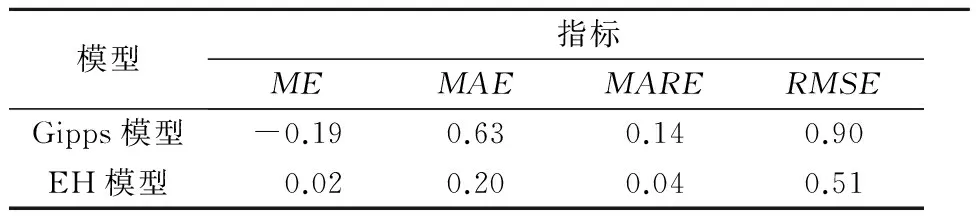
表2　模型数据误差结果

Gipps模型和EH模型的ME指标分别为-0.19和0.02，说明Gipps模型仿真得到的车速略小于实际值，这是由于Gipps模型采取安全间距作为期望间距，在跟驰中更加保守，而改进模型仿真得到的车速略大于实际值，但基本可以认为与实际相符.对于MAE，MARE和RMSE3项误差，EH模型的误差分别比Gipps模型的误差减小了63.5%，71.4%和43.3%，说明与Gipps模型相比，EH模型在对实际数据的拟合精度上具有较大的提高，能够更好地反应跟驰行为中驾驶员的驾驶行为.

3.2模型分析

在城市道路中，由于受到信号灯以及行人等影响，车辆在行驶过程中需要进行多次停车等待.一个基本的跟驰单元从车辆启动加速开始，当车速接近或达到期望车速后进入稳定跟车状态，前方出现交通拥堵时开始降低车速直至停车结束.实际的车辆行驶过程是由多个基本单元组成的，这里选取实测数据中的一个基本单元来比较不同跟驰模型的表现，所选的基本单元前后车速度和加速度随时间的变化曲线见图5～6.在模型仿真中，以实测的前导车速度为仿真中的前导车速度，分别用Gipps模型和EH模型控制跟驰车的运行，仿真得到的车辆速度、加速度和跟驰间距变化见图7～9.

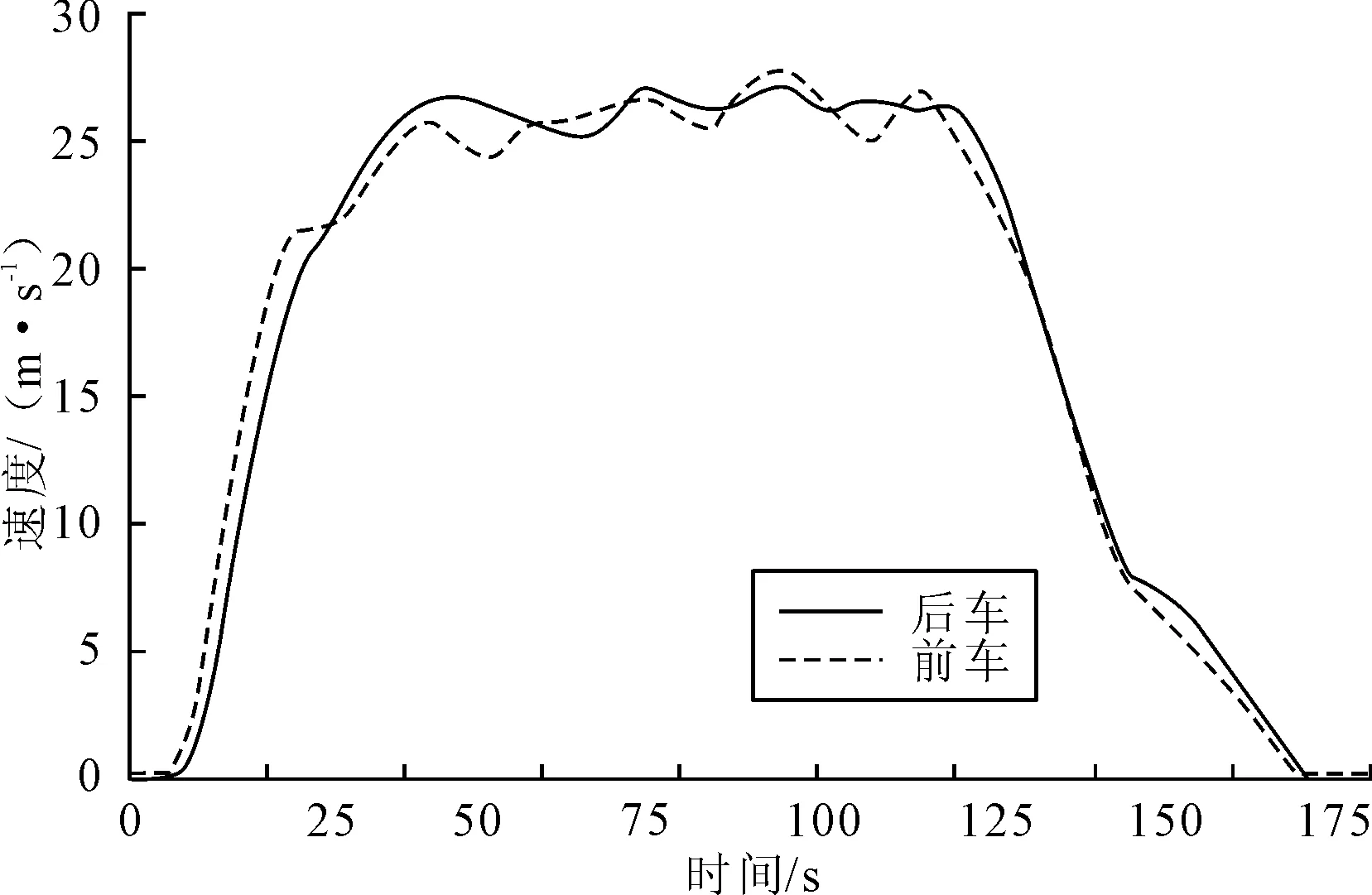
图5　实测跟驰速度时变图

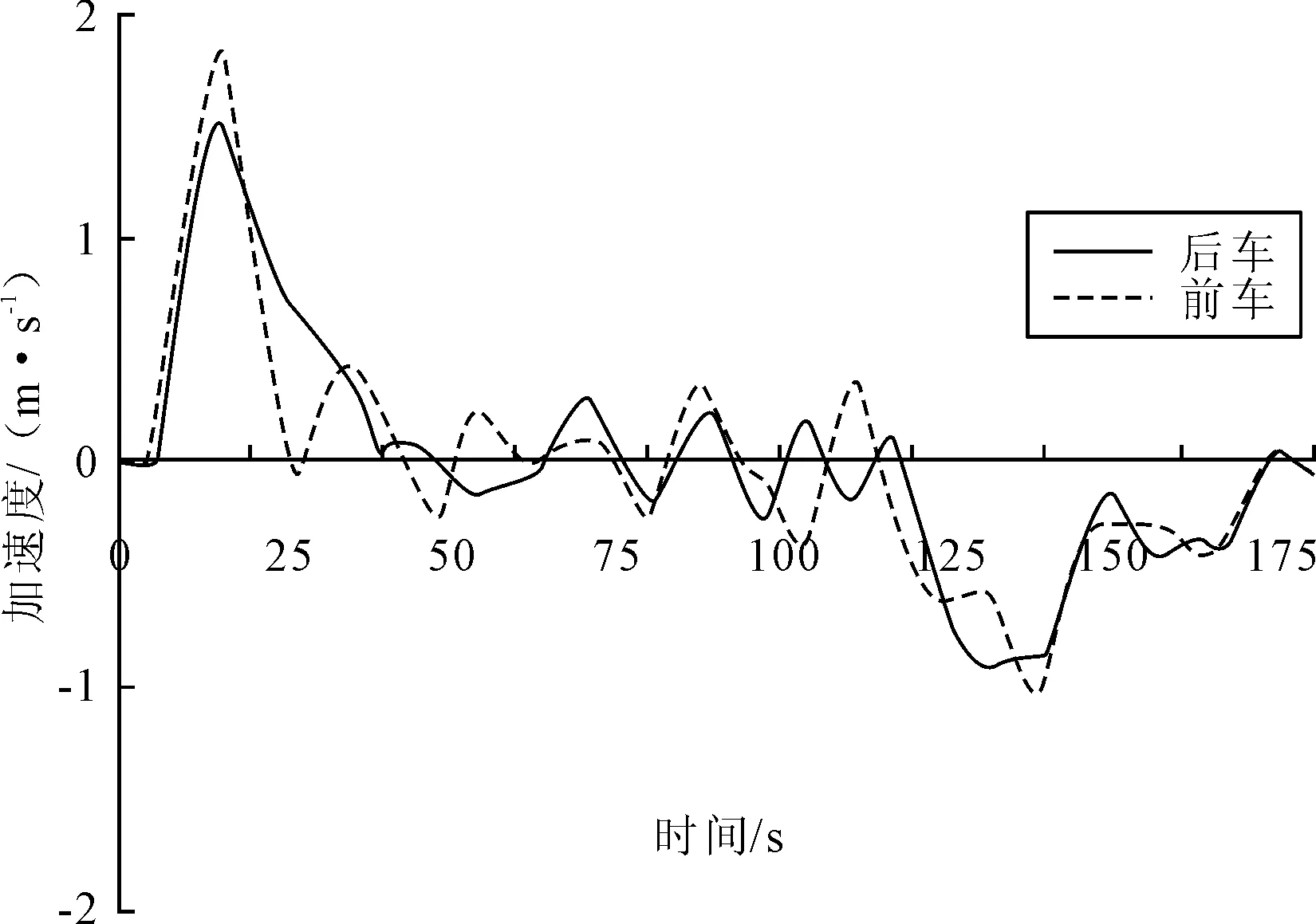
图6　实测跟驰加速度时变图

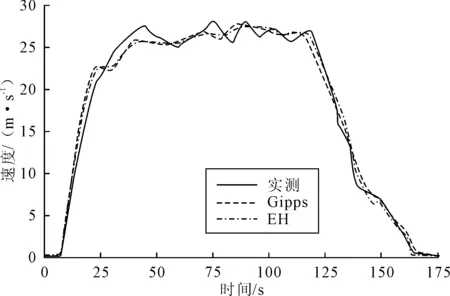
图7　实测与仿真速度时变图

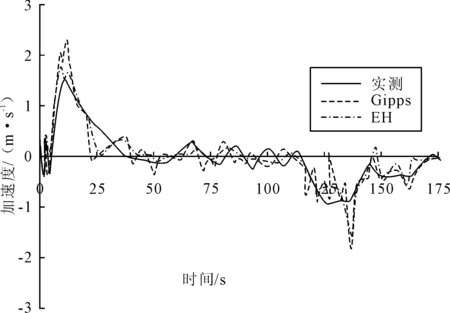
图8　实测与仿真加速度时变图

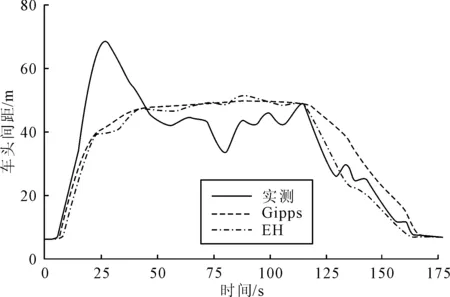
图9　实测与仿真车头间距时变图

在车辆启动时，实测数据的加速度峰值为1.5 m/s2，Gipps模型和EH模型仿真下的加速度峰值分别为2.3 m/s2和1.8 m/s2，均大于实际情况，但是仍在合理的范围内.实际加速度的持续时间较长，而Gipps模型则在第22 s时产生了轻微的减速行为，即该模型出现了过调节现象；而EH模型虽然没有完全符合实测加速度的大小，但是总体趋势较为一致.

在稳定跟驰时，两种模型均能较好的模拟后车随着前车运动状态的变化而变化、在实际驾驶行为中，由于驾驶员对间距和相对速度的判断存在误差，因此速度波动幅度较大，但是结合加速度的时变图可以看出，Gipps模型下的车辆加速度曲线存在较多锯齿，而EH模型下的车辆加速度曲线则较为平滑，更接近实际驾驶行为.

在减速停车时，两种模型的表现差异较大，主要体现在车头间距的变化上.Gipps模型下的车头间距大于实际数据且差距较大，Gipps模型下的车头间距与实测车头间距最大差值超过16 m，而EH模型仅有6.09 m.这是由于Gipps模型基于车辆动力学的安全距离对于前车速度减小较为敏感，因此在前车减速时采取较为保守的速度行为.

从整体可以看出，两种模型虽然与实际车辆运行状态略有差距，但均能较好地反应车辆跟驰中行为，与Gipps模型相比，EH模型在加速度的平顺性以及对车辆减速行为的模拟上表现更好.

4　结　　论

1) 运用高精度车载GPS设备获取的车辆运行数据具有较高精度，且获取的数据在跟驰行为分析和跟驰模型标定中的使用较为便捷.

2) 在统计规律上，跟驰车与前车的车头间距和跟驰车的速度之间有较为明显的指数曲线关系，可以通过数据拟合得到车辆的期望跟驰间距.

3) 通过实测数据拟合构建的跟驰模型相对于传统的安全距离模型在对实地数据的拟合上具有更高的精度.

4) 实测数据拟合的跟驰模型与安全距离模型均能够对跟驰行为进行再现，EH模型在加速度变化的平顺性以及车辆减速行为的仿真上比Gipps表现更好.

[1]REUSCHEL A.Vehicle movements in the column uniformly accelerated or delayed[J].Oesterrich IngrArch, 1950(4):193-215.

[2]PIPES L A.An operational analysis of traffic dynamics[J].Journal of Applied Physics,1953,2(4):274-281.

[3]BRACKSTONE M, MCDONALD M. Car-following: a historical review[J]. Transportation Research Part F: Traffic Psychology and Behaviour, 1999,2(4):181-196.

[4]王殿海,金盛.车辆跟驰行为建模的回顾与展望[J].中国公路学报，2012,25(1):115-127.

[5]CHANDLER R, HERMAN R, MONTROLL E W, et al. Traffic dynamics: studies in car following[J]. Operations Research, 1958,6(2):165-184.

[6]KOMETANI E, SASAKI T. Dynamic behaviour of traffic with a nonlinear spacing-speed relationship[J].General Motors, 1959(1):105-119.

[7]WIEDEMANN R. Simulation of road traffic in traffic in traffic flow[D]. Karlsruhe:University of Karlsrube(TH), 1974.

[8]KIKUCHI S, CHAKROBORTY P. Car-following model based on fuzzy inference system[J]. China Journal of Highway and Transport, 2001(1):55-58.

[9]曹金亮,史忠科,房雅灵.基于城市主干路交通流数据的跟驰模型标定[J].交通信息与安全,2014,32(6):82-88.

[10]SORIA I, ELEFTERIADOU L, KONDYLI A. Assessment of car-following models by driver type and under different traffic, weather conditions using data from an instrumented vehicle[J]. Simulation Modelling Practice and Theory, 2014(40):208-220.

Car-following Model Based on Expected Headway

YANG LonghaiZHAO ShunLUO Yi

(SchoolofTransportationScienceandEngineering,HarbinInstituteofTechnology,Harbin150090,China)

To research the car-following behavior, the field data of car-following are gathered by vehicles equipped with high precision GPS equipment under different speeds and traffic states. The relationships among the speed, headway, speed difference and acceleration are analyzed. Besides, a car-following model based on the expected headway (EH model) is built with the consideration of the analysis result. The EH model is compared with the Gipps model by parameter calibration and numerical simulation. The result shows that the EH model has a higher fitting precision with field data, and can better describe the behavior of deceleration and the change of the acceleration.

traffic flow; car-following model; GPS vehicle terminals; safety distance model

2016-06-12

U491.1

10.3963/j.issn.2095-3844.2016.04.003

杨龙海(1970- ):男，博士，副教授，主要研究领域为交通流理论、交通规划、交通仿真、交通环境保护