例析由递推数列求通项的几种巧妙方法
广东省惠州市第一中学 (516007 )
方志平
例析由递推数列求通项的几种巧妙方法
广东省惠州市第一中学(516007 )
方志平
由递推数列求通项公式是解决数列难题的瓶颈,也是自主招生考试及高中各类数学竞赛的热点之一,该内容具有良好的选拔功能.由于递推数列形式多变、复杂,解法灵活,技巧性高,从而导致这一内容成为学生学习的一个难点.本文总结出由递推数列求通项公式的几种巧妙方法,希望能够帮助广大高中生突破这一难点.
1.巧用待定系数法
例1a1=1,an=5an-1+(3n-7)·2n-1+4n-9(n≥2),求数列{an}的通项.
解:由a1=1,an=5an-1+(3n-7)·2n-1+4n-9(n≥2),令an+(An+B)2n+Cn+D=5{an-1+[A(n-1)+B]2n-1+C(n-1)+D},an=5an-1+(3An+3B-5A)×2n-1+4Cn+4D-5C,由待定系数法得:
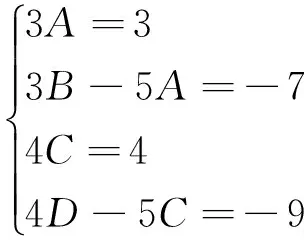
例2已知an+1=5an-6an-1+2n+1(n≥2),且a1=1,a2=-2.求数列{an}的通项.

点评:用待定系数法求解递推数列的通项公式,关键是观察递推关系式的特征,将递推关系式合理变形、组合转化为特殊数列,如上述两例都转化为等比数列.
2.利用公式变形法


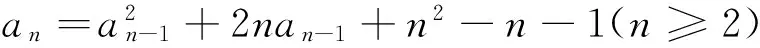
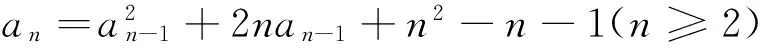
点评:这种方法类似于换元法,其实质是将递推关系式整体变形,构造一个新数列.
3.妙用引入参数法






点评:这里引入参数法解题,源于“利用特征方程法求解递推数列通项”的思想.其解法新颖、独特,可激发学生学习数学的兴趣,培养他们的创新能力!
4.使用代入消元法
例8若数列{an}及{bn}满足


点评:消元法就是利用方程的思想,将二元线性递推式中消去一个元,将二元线性递推数列化为一阶或二阶线性递推数列.本题也可仿例5“引入参数法”求解,读者可尝试.
综上几种方法是把一些较难处理的由递推数列求通项问题,巧妙转化为我们所熟悉的特殊数列问题,从而使问题迎刃而解.另外,使用上述这些巧妙方法能降低思维强度,简化推理和运算过程,避免了复杂的运算,提高了解题效率.

