构造“好”函数,巧证不等式
——对2016年全国1卷(乙卷)理科数学第21题反思
南昌三中
张金生
构造“好”函数,巧证不等式
——对2016年全国1卷(乙卷)理科数学第21题反思
南昌三中
张金生
函数、导数与不等式是中学数学中最重要的内容,近年来函数导数不等式题型常作为高考压轴题,对考生来说如何根据所要证的不等式构造恰当的函数,利用导数研究函数的单调性,借助单调性比较函数值的大小,以期达到证明不等式的目的是一个难点.本文以今年全国 1 卷 (乙卷) 理科数学第21题和几道模拟试题为例,说明如何构造一个好函数,求导研究函数的性质,利用函数的单调性和极值等性质去解决问题,希望能抛砖引玉.
一、极值点偏移的问题,根据对称化构造“好”函数
例1(2016 年全国 1 卷 (乙卷) 理科数学第21题)已知函数f(x)=(x-2)ex+a(x-1)2有两个零点.(1)求a的取值范围;(2)设x1,x2是f(x)的两个零点,证明:x1+x2<2
分析:该题第 (1) 小题是典型的零点个数问题,可用分离变量法,建立一个新函数,求导研究函数图象和性质,考查了函数与方程、分类讨论与数形结合思想;第 (2) 小题是典型的极值点偏移的问题,根据对称化构造一个函数即可.
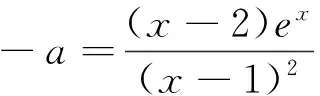
(2)由(1),不妨设x1<1 该题并不陌生,目前全国各地的模拟题中频繁出现极值点偏移的试题,比如下面例题2: 例2(南昌市2015-2016重点中学高三月考21题) 所以2016 年全国 1 卷 (乙卷) 理科数学第21题对学习能力强知识面广的考生较有利. 构造函数在解决不等式等问题中之所以显示出这么大的作用,根源在于函数思想的巨大威力,正如大数学家笛卡儿所说:一切问题都可以转化为数学问题,一切数学问题又可以转化为函数问题.而构造函数正是将问题转化为函数问题的首要一步,如何学会构造恰当的函数,应用函数的性质去解决问题请继续看以下例题. ∴以Q为坐标原点,分别以QA,QB,QP为x,y,z轴建立如图所示空间直角坐标系o-xyz. 解:(Ⅰ)切线方程y=2x-1. 例4已知函数f(x)=ln(1+x)-x,g(x)=xlnx.(1)求函数f(x)的最大值; 通过以上典例的分析,可以看出构造一个“好”函数不但是一种解题的好方法,也是掌握函数与方程思想的一条好途径.将证明或求解的不等式转化为函数的问题,然后利用求导去研究函数性质证明不等式,关键在于转化为什么样的函数.这就要求从被证(解)的不等式的形状,特点入手,发生联想.本着“纵向深入,横向联系”的原则,合理的构造函数模型.达到启发学生思维,开拓解题途径的效果.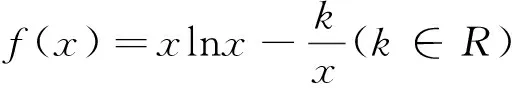
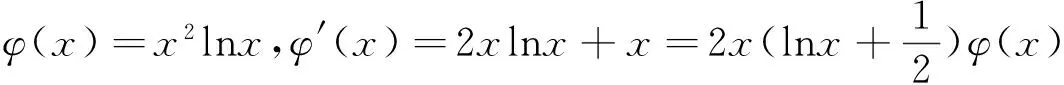
二、引入新变量,构造“好”函数




二、巧设主元,构造“好”函数

