高考解析几何大题考向定位及解题策略

甘肃省永昌县第一高级中学　(737200)

赵忠平



高考解析几何大题考向定位及解题策略

甘肃省永昌县第一高级中学(737200)

赵忠平

解析几何大题是近年来高考的重点和热点问题.归纳总结高考解析几何大题的常见类型及求解策略能够帮助学生快速识别解析几何题型模式,并有针对性地选择解题方法，准确解决解析几何问题.本文总结解析几何大题中的几种常见类型，指出其相应的解题策略，供参考.

一、弦长面积型

点评：直线与曲线相交问题弦长是解题的重要抓手，而解决与弦长和面积有关的问题，一般可以利用韦达定理来表示有关量.

二、对称型

例2在抛物线y2=4x上恒有两点关于直线y=kx+3对称，求k的取值范围.

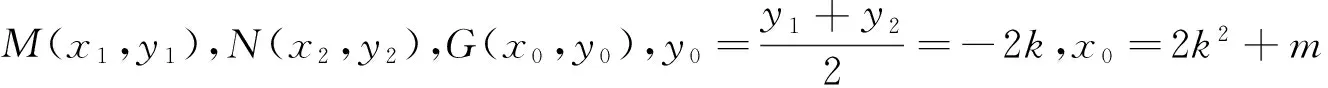
点评：对称型问题一般可以用“点差法”或“参数法”求解，要注意利用对称的条件进行巧设未知量，从而达到简化运算的目的.

三、定点、定值型

例3ADB为半圆，AB为半圆直径，O为半圆圆心，且OD⊥AB，Q为线段OD的中点，已知|AB|=4，曲线C过Q点，动点P在曲线C上运动且保持|PA|+|PB|的值不变.(1)建立适当的平面直角坐标系，求曲线C的方程；

解析：(1)略.

点评：定点定值问题一般利用曲线定义、方程特征等抓住变化过程中的不变量，利用过定点直线系方程和韦达定理通过“设而不求”的方法求解.

四、最值范围型

例4已知椭圆C的中心在原点，焦点在x轴上，以两个焦点和短轴的两个端点为顶点的四边形是一个面积为8的正方形(记为Q).

(1)求椭圆C的方程；(2)设点P是椭圆C的左准线与x轴的交点，过点P的直线l与椭圆C相交于M、N两点，当线段MN的中点G落在正方形Q内(包括边界)时，求直线l的斜率的取值范围.

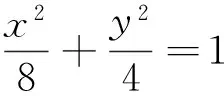
点评：最值范围问题一般是利用题目条件找出不等量关系列不等式组求解或表示出目标函数，再求目标函数的值域.

五、证明型

证明：点P在C上；(2)设点P关于O的对称点为Q，证明：A、P、B、Q四点在同一圆上.

点评：证明型解析几何问题一般以验证结论为主要方法，即利用韦达定理表示求解有关量，进而验证结论的正确性.

六、探索型

例6已知圆C:x2+y2-2x+4y-4=0，问是否存在斜率为1的直线l，使l被圆C截得弦为AB，以AB为直径的圆经过原点O，若存在写出l的方程，若不存在，说明理由.

点评：探索型问题一般假设存在，用待定系数法求解，若推出矛盾说明不存在，若求得合适解说明存在.