也谈一道美国数学月刊问题的再加强
广东广雅中学 (510160)
杨志明
也谈一道美国数学月刊问题的再加强
广东广雅中学(510160)
杨志明

文[2]给出这个不等式的加强,即
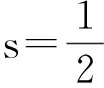
文[3]给出这个不等式的加强,即
本文对上述问题进行再加强,得到如下
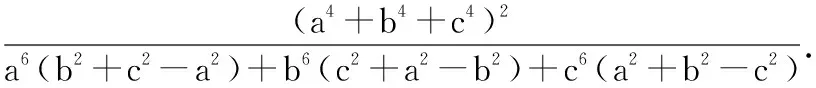
由(5)式知,要证明(4)式成立,只需证明16Δ2(a4+b4+c4)≥a6(b2+c2-a2)+b6(c2+a2-b2)+c6(a2+b2-c2).(6)
由海伦公式知,
16Δ2=2(a2b2+b2c2+c2a2)-(a4+b4+c4).(7)
由(7)式知,(6)式等价于[2(a2b2+b2c2+c2a2)-(a4+b4+c4)](a4+b4+c4)≥3[a6(b2+c2-a2)+b6(c2+a2-b2)+c6(a2+b2-c2)]⟺2(a8+b8+c8)+2a2b2c2(a2+b2+c2)≥(a6b2+a2b6+b6c2+b2c6+c6a2+c2a6)+2(a4b4+b4c4+c4a4).(8)
令a2=x,b2=y,c2=z,则(8)式等价于2(x4+y4+z4)+2xyz(x+y+z)≥x3y+xy3+y3z+yz3+z3x+zx3+2(x2y2+y2z2+z2x2).(9)
由3元4次Schur不等式知,x4+y4+z4+xyz(x+y+z)≥x3y+xy3+y3z+yz3+z3x+zx3.(10)
由(10)式知,要证明(9)式成立,只需证明x3y+xy3+y3z+yz3+z3x+zx3≥2(x2y2+y2z2+z2x2)(11)
⟺xy(x-y)2+yz(y-z)2+zx(z-x)2≥0.显然.
由三元均值不等式知,3(a4+b4+c4)≥(a2+b2+c2)2,故(4)式比(3)式强.
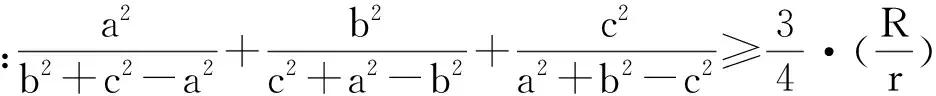
证明:由常见的三角形恒等式[3]:a+b+c=2s,ab+bc+ca=s2+4Rr+r2,w=abc=4sRr(其中s,R,r分别为ΔABC的半周长、外接圆和内切圆半径)知,u=a2+b2+c2=(a+b+c)2-2(ab+bc+ca)=(2s)2-2(s2+4Rr+r2)=2(s2-4Rr-r2),v=a2b2+b2c2+c2a2=(ab+bc+ca)2-2abc(a+b+c)=(s2+4Rr+r2)2-16s2Rr.
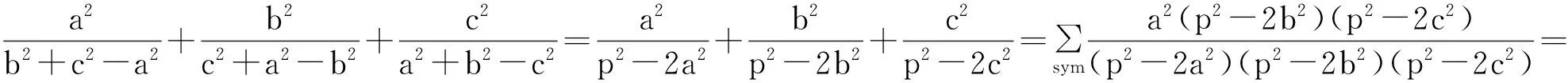
因此,原不等式等价于
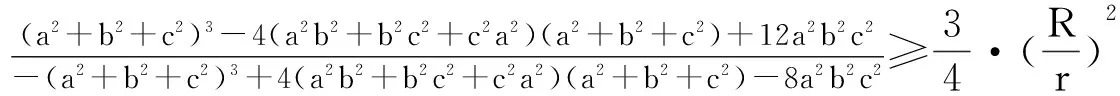
由Euler不等式:R≥2r和Gerretsen不等式知,s2≤4R2+4Rr+3r2知,上式成立.
[1]Proposed by Cezar Lupu.Problem11527.The American Mathematical Mothly[J].2010,117(8):742.
[2]崔 超, 沈南山,邹根兰.一道美国数学月刊问题的再加强[J].中学数学教学,2015,2.
[3]兰小兵.一道美国数学月刊问题的再加强[J].中学数学教学,2016,1.
[4]陈胜利 关于R,r与s的锐角三角形不等式.见:几何不等式在中国,江苏教育出版社,1996年6月:72-78.

