压缩感知在传感器节点信息采集中的应用*

赵　磊， 俞阿龙,2， 徐冬平， 孙诗裕

(1.宁夏大学 物理电气信息学院，宁夏 银川 750021;2.淮阴师范学院 物理与电子电气工程学院，江苏 淮安 223300;3.南京工业大学 自动化与电气工程学院， 江苏 南京 211866)



应用技术

压缩感知在传感器节点信息采集中的应用*

赵磊1， 俞阿龙1,2， 徐冬平3， 孙诗裕3

(1.宁夏大学 物理电气信息学院，宁夏 银川 750021;2.淮阴师范学院 物理与电子电气工程学院，江苏 淮安 223300;3.南京工业大学 自动化与电气工程学院， 江苏 南京 211866)

随着无线传感器网络的快速发展，海量数据的处理、存储与传输给传统的以高速ADC和存储通信设备带来了巨大的压力。由于传感器节点采集的感知数据具有时间相关性，本文提出基于压缩感知理论的采样压缩方法，其打破了传统奈奎斯特采样定理的限制，在前端只需远低于奈奎斯特采样频率采样信号就可以完成对原始信号的精确重构，并构造了基于压缩感知的模拟信息转换器(AIC)模型。最后通过以Matlab为平台进行实验仿真，结果表明:该模型可以用较少的观测值即可精确重构稀疏信号，并且其重构精度与观测数M、稀疏度K有关。

压缩感知； 模拟信息转换器； 稀疏信号

0　引　言

以往数字信号处理的前端使用的都是模拟数字转换器(analog-to-digital convertor,ADC),它是基于传统地香农定理来设定的，认为为了不失真地恢复模拟信号，采样频率应该不小于奈奎斯特频率(即模拟信号频谱中的最高频率)的2倍。面对海量数据的处理与存储，目前的ADC器件已不能满足实际的需求。

近年来，国内外不少学者也做了不少研究工作，主要有基于节点数据相关性的压缩算法、基于数据传输特性和封包结构的压缩方法和基于预编码的数据压缩算法。但作为传统的压缩方法有明显的缺陷：首先压缩过程要完整的原始信号，其次在计算出完整的投影后需要丢弃大部分分量，浪费计算资源[1]。因此，本文提出基于压缩感知(compressed sensing,CS)的数据压缩方法，它为需处理海量数据量的无线传感器网络带来了新的思路。

压缩感知理论表示对于N维信号，压缩感知只需要其在观测矩阵的线性投影，即可得到压缩后观测向量，由M(M≪N)个观测向量就能重构出原始信号[2,3]。由于对海量数据处理时，传统的奈奎斯特采样的硬件结构复杂、成本高、数据处理的过程中造成大量的浪费。

本文提出的基于压缩感知的模拟信息转换器(AIC)，其可将稀疏信号以远低于奈奎斯特采样频率进行信号采集，并在后端利用重构算法精确恢复数据。

1　压缩感知理论

压缩感知理论摒弃了传统压缩系统先以奈奎斯特采样速率采样再压缩的方法，而是边采样边压缩，即实现的不再是ADC，而是AIC。压缩感知理论由Donoho等人提出，压缩感知理论表示：如果信号通过某种变换(如傅立叶变换、小波变换等)后，是可稀疏表示或可压缩的，则可设计一个与变换基不相关的测量矩阵测量信号，得到的测量值通过求解优化问题，可实现信号的精确或近似重构[3]。

如图1和图2所示就是传统采样与压缩感知采样的对比。

图1　传统的采样Fig 1　Traditional sampling

图2　压缩感知理论的采样Fig 2　Sampling of compressed sensing theory

综上压缩感知理论分为三部分：信号的稀疏表示、测量矩阵的构建、信号的重构。

1.1信号的稀疏表示

信号的稀疏表示是压缩感知理论的前提条件。考虑一个长度为N的一维离散实值信号X，可以看作是RN空间中的一个N×1维的列向量X=[x1,x2,…,xN]T.如果X仅有少量的非零分量，或者说非零分量的个数k≪N,就称信号X本身是稀疏信号。

给定RN空间中的一组标准正交基：{φi|i=1,2,3,…N},其中,向量φ是RN空间中N×1维的列向量，则RN空间中的任意X都可以由{φi=1,2,3,…N}线性表示为

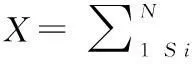
(1)

一般来说，普通的信号在时域都是非稀疏的。因此，要应用压缩感知，首先要对信号进行变换，以找到信号的稀疏域，一般信号在小波基、傅里叶基和DCT基中都是稀疏的[4]。

2.2测量矩阵的构建

测量矩阵的构建是压缩感知理论的核心。它是用一个测量矩阵(M≪N，M为行，N为列)和信号相乘，就是利用测量矩阵将稀疏过后的信号进行投影得到信号的采样值

Y=φX=φφSi=ASi

(2)

式中Y=[y1,y2,…,yN]T是采样信号，φ是测量矩阵，A是感知矩阵，X是N维原始信号，Y是M维测量信号。测量值Y是一个M×1的矩阵，这样使得原始值从N维降到了M维的测量值。观测过程是非自适应的，即测量矩阵φ不依赖于信号X。测量矩阵的设计要求信号从X转换到Y后，能精确重构出原始信号。

已证明由于信号是K稀疏的(K≪M)，若A满足有限等距性质(restrictedisometryproperty，RIP)[5], 即对于任意K稀疏信号X和常数δk∈(0,1)，矩阵A满足

(3)

目前，用于压缩感知的测量矩阵主要有高斯随机矩阵、傅立叶随机矩阵以及伯努利矩阵等[5]。

2.3信号的重构

信号的重构是压缩感知理论的重要保证，即从M维的测量值Y恢复N维的原始信号X，由于M≪N，直接求解Y=φX的逆问题是一个病态问题。但是如果信号X是稀疏的，即有K个非零系数，只要M满足

M≥CK(C≈lg(N/M)≪N

(4)

就可以求解变换稀疏信号Si，再带回式(1)进一步恢复出信号X。

信号的重构原本属于对0范数的求解问题。但0范数属于数学上一个NP-hard问题，是无法解决的，所以,不能直接用求0范数来重构信号。在这种情况下，提出了两种方法：

1)将求解最小0范数的问题转换为最小1范数，因为最小1范数具有可凸优化特点，所以,可以转化为线性规划问题求解,即转化为

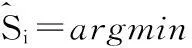
(5)

最小1范数问题又称为基追踪(basis pursuit,BP)[6]。式(5)中的最小l范数问题是一个凸优化模型，可以得到精确的解，但是计算量较大，在通信中恢复高维信号时很困难。

2)转而求最小0范数问题的次最优解，贪婪算法是解决此类问题最有效实用的方法，是目前应用非常广泛的压缩感知信号重构算法。贪婪算法是允许一定的误差ζ，求解以下的最小0范数问题

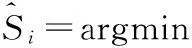
(6)

常用的贪婪算法有MP算法、OMP算法等等。

2　基于时间相关性的压缩感知

在传感器节点中，由于在邻近时刻采集的感知数据会有很大的相似性，因此,可通过消除节点邻近时刻感知数据的时间冗余来进行数据压缩[7]。针对感知数据内部结构相关性的特点，提出了基于压缩感知的模拟信息转换器和重构算法。

2.1压缩感知的AIC结构模型

对于海量数据处理的瓶颈问题，合理地利用基于压缩感知的模拟信息转换器已成为解决问题的必然趋势。AIC代替ADC的数字系统简单结构图如图3所示。

图3　AIC信息处理系统Fig 3　Information processing system of AIC

模拟信号X(t)经过AIC器件降维处理得到信息矢量Y(m),由于AIC器件采样的仅仅是少量的信息样点输出速率较低，后端可直接采用数字信号处理器(DSP)完成信号重构。

针对上述问题提出适用于连续模拟信号场合的预调制型AIC结构[8]。其硬件框图如图4所示。

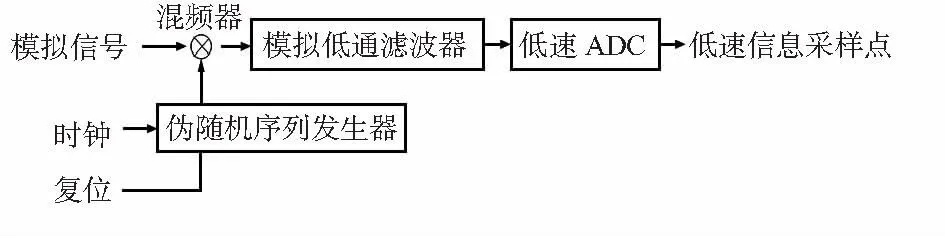
图4　预调制型AIC结构模型Fig 4　AIC structure model for preset type

预调制型AIC结构简单由伪随机序列发生器、混频器、模拟低通滤波器以及低速模数转换器组成。在一时间内，通过伪随机序列发生器产生的随机序列与AIC器件的模拟输入信号X(t)经过混频器相乘，将调制过后的信号再经低通滤波器滤波，即积分处理，最后用低速ADC以远低于奈奎斯特采样频率进行采样量化处理。

2.2正交匹配追踪重构算法

常用的贪婪算法是正交匹配追踪(orthogonalmatchingpursuit,OMP) 算法。优点是重构时间短，在现实生活中得到广泛的运用。本文采用经典常用的OMP算法进行信号重构，其算法流程如下：

输入：感知矩阵A，测量信号Y，原始信号X的稀疏度为K

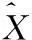
初始化：残差r0=Y，索引集Λ=φ,t=1

1)首先，找出感知矩阵的列与残差内积中最大值对应的角标λ，即

λi=argmaxj=1…N|〈rt-1,Aj〉|

(7)

2)更新索引集

Λt=Λt-1∪{λt}

(8)

记录找到的感知矩阵中的重建原子集合

At=[AT-1,Aλt]

(9)

3)由最小二乘法得到

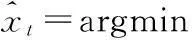
(10)

4)更新残差

(11)

5)判断是否满足t>K，若满足,则迭代停止;若不满足,则重复步骤(1)。

3　仿真实验

在Matlab/Simulink平台上构建AIC模型，并通过Matlab编程对压缩后的信号进行重构。具体流程如图5所示。

图5　压缩感知仿真流程Fig 5　Simulation process based on CS

采样文献[4]传感器采集的数据进行仿真实验。原始数据X[N],N=1,2,3,…,250，稀疏度K=8，首先在小波基上对原始数据进行稀疏分解，再将压缩后的观测值Y[M],M=1,2,3,…,50，最后将新数据Y[M]利用OMP算法进行重构，重构的新数据与原始数据对比图如图6所示。

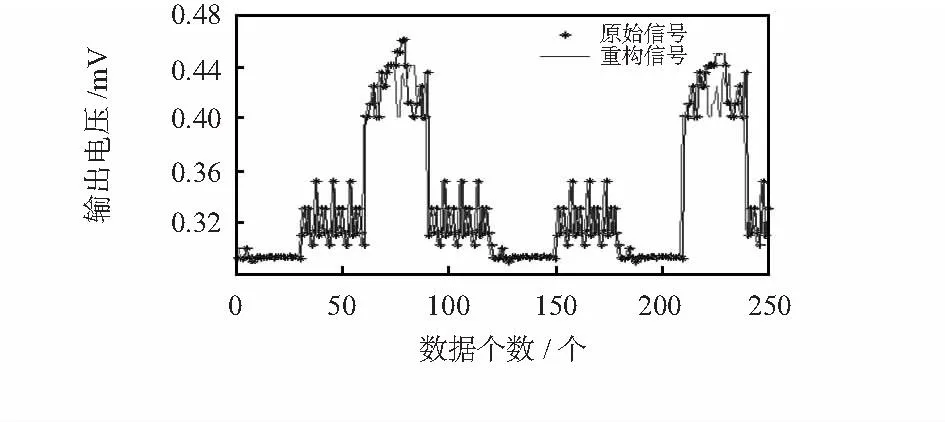
图6　原始信号与重构信号对比图Fig 6　Contrast figure of original signal and reconstructed signal

为了进一步对压缩重构性能进行完善，还需调节稀疏度K与观测值M的值,找到合适的K与M使得重构误差最小。

归一化重构误差定义为

(12)

K=8，4，2时，不同观测值M情况下的重构结果如表1所示。

若误差允许在0.1，从表1可以看出:当稀疏度K=8，观测数M≥35时，重构误差小于0.1，可较好地重构原始信号；当稀疏度K=8，观测数M≥25时，重构误差小于0.1，可较好的重构原始信号；当稀疏度K=8，观测数M≥15时，重构误差小于0.1，可较好地重构原始信号。

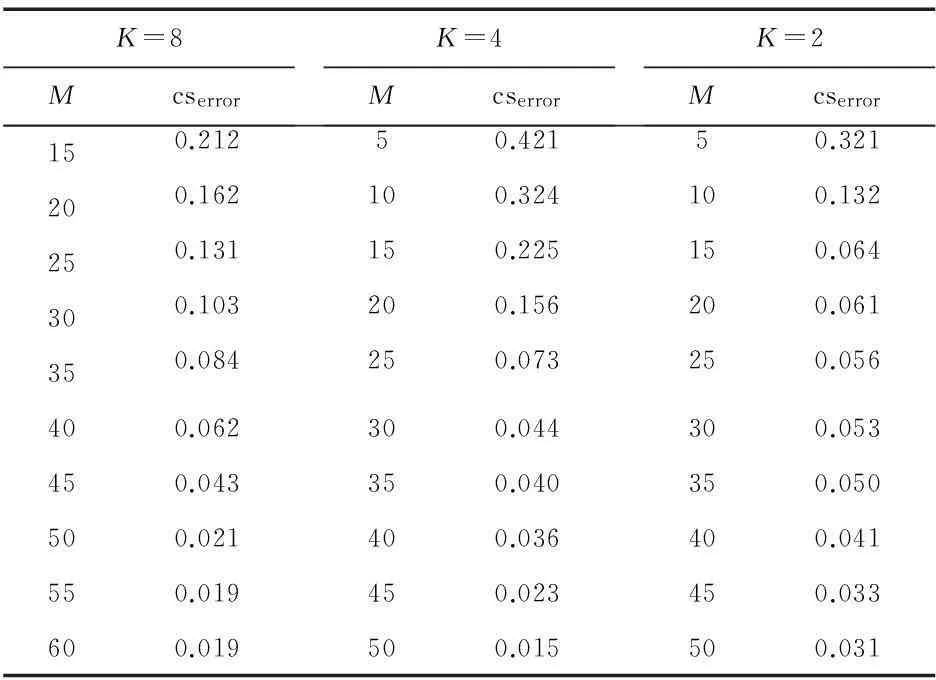
表1　当K=8,4,2的不同M下的重构误差cserror

4　结　论

针对高速的奈奎斯特采样定理，本文提出基于压缩感知的传感器节点信息采集方法。首先阐述了压缩感知理论的三大核心问题，接着对传感器节点信息采集时相邻时刻存在时间冗余，提出基于压缩感知的模拟信息转换器模型与OMP重构算法,最后通过Matlab对250个数据进行仿真，并通过调节观测值M与稀疏度K对重构误差进行分析，说明重构精度与M和K有关。

[1]Heinzelman W B,Chandrakasan A P,Balakrisnan H．An application-spicific protocol architecture for wireless micro sensor networks[J]．IEEE Transactions on Wireless Communications,2002,12(1):660-670.

[2]Donoho D.Compressed sensing[J].IEEE Trans on Information Theory,2006,52(4):1289-1306.

[3]叶志申,张绍钧,黄仁泰.压缩感知理论及其重构算法[J].东莞理工学院学报,2010,17(3):56-58.

[4]龚静.无线传感器网络中基于压缩感知技术的数据压缩方法研究[D].成都:西南交通大学,2011:23-24.

[5]卢雁.压缩感知理论综述[J].计算机与数字学报,2012,3(8):34-35.

[6]Chen S,Dohono D,Saunders M.Atomic decomposition by basis pursuit[J].SIAM Review,2001,43(1):129-159.

[7]Lindsey S,Pegasis Craghavendre.Power-efficient gathering in sensor information sysetens[J]．IEEE Trans on Parallel and distributed Systems,2002,13(9):924-932.

[8]陈宇科,汪立新,潘高峰.压缩采样中的模拟信息转换技术研究[D].杭州:杭州电子科技大学,2011:56-57.

俞阿龙，通讯作者，E—mail：yal@hytc.edu.cn。

Application of compressed sensing in sensor node information collection*

ZHAO Lei1, YU A-long1,2, XU Dong-ping3, SUN Shi-yu3

(1.School of Physics Electrical Information,Ningxia University,Yinchuan 750021,China;2.School of Physics and Electronic Electrical Engineering,Huaiyin Normal University,Huai’an 223300,China;3.School of Automation and Electrical Engineering,Nanjing University of Technology,Nanjing 211816,China)

With the rapid development of wireless sensor networks(WSNs),processing,storing and transmitting huge amounts of data for traditional ADC at high speed and storage communication equipment has brought great pressure.Due to the time of sensory data from the sensor node has a correlation,put forward sampling and compression method based on compressed sensing theory,it breaks the limitation of traditional Nyquist sampling theorem,in the front just is far lower than the Nyquist sampling frequency sampling signal can complete the accurate reconstruction of the original signal,and construct model analog-to-information convertor(AIC),based on compression perception using platform of Matlab simulation experiment is carried out,the results show that the model can accurately reconstruct sparse signal using less observations,and the reconstruction precision is related to the observed numberMand the sparse degreeK.

compressed sensing(CS); analog-to-information convertor(AIC); sparse signal

2015—10—26

国家自然科学基金资助项目(61350008)；江苏省高校产业化推进项目(JHB2012—55)

TP 274

A

1000—9787(2016)08—0141—03

赵磊(1992-)，男，江苏淮安人，硕士研究生，主要研究方向为无线传感器与智能系统。

DOI:10.13873/J.1000—9787(2016)08—0141—03