近邻点联合测距修正粒子群优化定位算法*

王　哲， 李　平

(长沙理工大学 计算机与通信工程学院，湖南 长沙 410114)



近邻点联合测距修正粒子群优化定位算法*

王哲， 李平

(长沙理工大学 计算机与通信工程学院，湖南 长沙 410114)

针对在信标节点随机分布的环境中传统测距差分修正定位算法对参考节点选取过于单一，导致测距修正系数误差较大的问题，提出了一种近邻点联合测距修正粒子群优化的定位算法。它利用一种近邻点联合测距修正算法得到未知节点到各信标节点的修正距离，然后通过一种改进的粒子群优化 (PSO) 算法对定位结果进行优化，得到未知节点的估计位置。仿真结果表明：改进定位算法与传统算法相比，有效地提高了定位精度和稳定性。

无线传感器网络； 近邻点; 接收信号强度指示； 差分修正； 粒子群优化

0　引　言

无线传感器网络(wireless sensor networks,WSNs)是一种应用广泛的没有基础设施的自组织无线网络[1]，其成本低、功耗小，具有优良的性能。节点位置信息成为研究WSNs技术和应用的核心领域之一。基于接收信号强度指示(RSSI)的测距技术是通过在传播过程中不断衰减的信号强度来估算距离[2]，在WSNs定位技术中大量被采用。但对无线传感器来说反射、多径传播、天线增益等问题都会对RSSI产生传播损耗，如何提高基于RSSI的定位精度是个难题[3]。

文献[4]从不同角度研究了基于RSSI的无线传感器网络测距模型，引入一种立体式分层思想，提出了一种基于RSSI误差修正的待测节点定位算法，具有良好的稳定性。文献[5]在对测距误差的差分修正中，仅仅选取一个参考节点，这对未知节点定位决定权过大，并且这个点的选取也不合理。文献[6]提出了加入罚函数的粒子群优化(PSO)定位算法，该罚函数的约束条件对所有信标节点都使用统一的测距误差作为测距修正系数，这并不合理。

针对上述算法尚未解决的问题，本文提出一种定位误差较小的基于近邻点联合测距修正PSO的定位算法。

1　传统的测距差分修正定位算法

对无线传感器来说，RSSI易受环境影响产生显著的传播损耗，仅仅考虑两节点通信的RSSI来测距，可能带来较大的误差。针对该缺陷测距差分修正算法可在一定程度上减小这种误差。

传统测距差分修正算法[7]通常令距离未知节点最近的信标节点为差分参考节点，其余的每个信标节点以该参考节点为基准，通过真实距离和测量距离计算得到各自的距离差分修正系数，利用它来修正各信标节点到未知节点的测量距离从而得到修正距离。然后利用加权质心定位算法得到最终的未知节点的估计位置。

2　算法的改进与实现

传统测距差分修正算法中各修正系数的计算完全依赖距离未知节点最近的一个信标节点，若它距未知节点很近则定位效果较好，但实际环境中该条件往往很难满足，且对整个WSNs来说仅选取单个参考节点不足以反映每个信标节点的测距误差情况。本文提出一种近邻点联合测距修正PSO的定位算法，该算法得到的未知节点到每个信标节点的修正距离误差较小，然后利用一种改进的PSO算法对定位结果进行优化，有效地提高了定位精度。

2.1近邻点联合测距修正算法

本文将基于RSSI的测距序列中距离未知节点最近的k个信标节点称为近邻k点(Nrtk)，假设信标节点A1为Nrt1，信标节点A1和A2为Nrt2。

定义1 信标节点Ai与Aj间的测距误差因子为ρij，反映两个节点间的测量距离与真实距离间的差异,ρij为

(1)

定义2 Nrt1情况下,信标节点Aj到未知节点的测距修正系数为

(2)

式中w1为Nrt1情况下的修正权重。以Nrt1为重点参考节点，其余信标节点为一般参考节点，用φj来修正未知节点到第j个信标节点的距离。

定义3 Nrt2情况下,信标节点Aj到未知节点的测距修正系数为

(3)

式中w2为Nrt2情况下的修正权重。

从仿真结果(第3章)看，对Nrt3及更多的近邻点，其测距修正系数计算量大、通信能耗增大，且不能带来定位精度的提高，因篇幅有限本文重点考虑Nrt1和Nrt2两种情况。

定义4 未知节点到信标节点Aj的测距修正方程

(4)

通过式(4)可得到未知节点到每个信标节点的修正距离dj。

在节点定位阶段本文采用改进的PSO算法来优化定位结果。PSO算法不仅对测量误差的敏感度非常低，并且能够快速地找到最优解，从而提高定位精度[8]。

2.2基于改进的PSO法优化定位结果

PSO的模型是“速度+位置”，在一个解空间里有大量的粒子，粒子被看成搜索空间中的一个点，粒子在飞行过程中，其速度和位置依靠个体最优值pbest和全局最优值gbest不断进行更新，进而帮助粒子不断靠近最优解处[9]。若在二维搜索空间中，X=[X1,X2,…,Xm]表示由m个粒子组成的种群，第i个粒子的坐标为Xi=(xi1,xi2)，速度为Vi=(vi1,vi2)，则速度与位置更新公式如下

Vi(t+1)=wVi(t)+c1r1[pbesti-Xi(t)]+

c2r2[gbest-Xi(t)]

(5)

Xi(t+1)=Xi(t)+Vi(t+1)

(6)

式中c1,c2为加速因子，r1,r2为(0,1)区间呈均匀分布的随机数，w为惯性权重，Vi(t),Vi(t+1)分别为粒子的当前速度和更新后速度，Xi(t),Xi(t+1)分别为粒子当前位置和更新后位置。

优秀进化算法应具备早期较好的全局探索能力和后期好的局部开发能力，PSO算法中惯性权重w是平衡粒子的全局及局部搜索能力的关键。为避免粒子在全局最优解附近出现振荡现象，做如下改进：随着迭代次数的增加，惯性权重w由最大wmax线性减小到最小wmin，这样就能够保证优化初期w能在较长时间段内维持较大值，提高全局搜索能力，而优化后期提高局部搜索能力。w表示为

(7)

式中t为当前迭代次数，T为最大迭代次数。

搜索的后期空间中的粒子常会处于相对稳定的状态，减缓了搜索速度，严重影响了粒子收敛最优解的速度，从而陷入局部最优[10]。当迭代过程中检测到早熟迹象时对种群引入一种非一致性变异调整，过程如下：

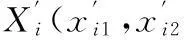
(8)

(9)

式中Δ(t,y)的表达式为

Δ(t,y)=y×(1-r(1-t/T)λ)

(10)

式中r为[0,1]的随机数，λ是非一致性的程度，取值范围一般为[2，5]。

该变异调整机制能帮助粒子尽快跳出局部最优区域，进而有效地减少无效迭代次数，提高了算法的搜索和开发能力。

改进PSO算法步骤如下：

1)搜索域内随机初始化k个粒子。

2)根据式(11)计算各粒子的个体目标函数值，各粒子的个体最优位置放于自己的pbest中，群体最优位置放于gbest中。个体目标函数为

(11)

式中(xi,yi)为第i个信标节点坐标，(x,y)为个体粒子坐标，f的极小值为要求的定位坐标。

3)更新调整惯性权重、粒子的速度和位置，若检测到有粒子陷入早熟，采用变异调整机制。

4)比较每个粒子个体最优位置、全局最优位置，如果当前位置优于个体最优位置，则其替换为该粒子的个体最优位置；如果当前位置优于全局最优位置，则其替换为粒子群全局最优位置。

5) 当粒子的个体目标函数值足够小或已达到最大迭代次数时，停止更新，最优解的位置为未知节点的估计位置;否则,返回步骤(2)继续更新。

3　算法仿真和分析

本文采用Matlab实验平台进行算法仿真实验。

3.1仿真环境与参数设定

仿真的网络拓扑结构如下：网络中的所有节点都是随机生成的，在同一个的网络环境中进行100次仿真实验，对实验结果取平均值。采用对数-常态分布无线传播模型模型计算RSSI[11]，网络参数如表1所示。

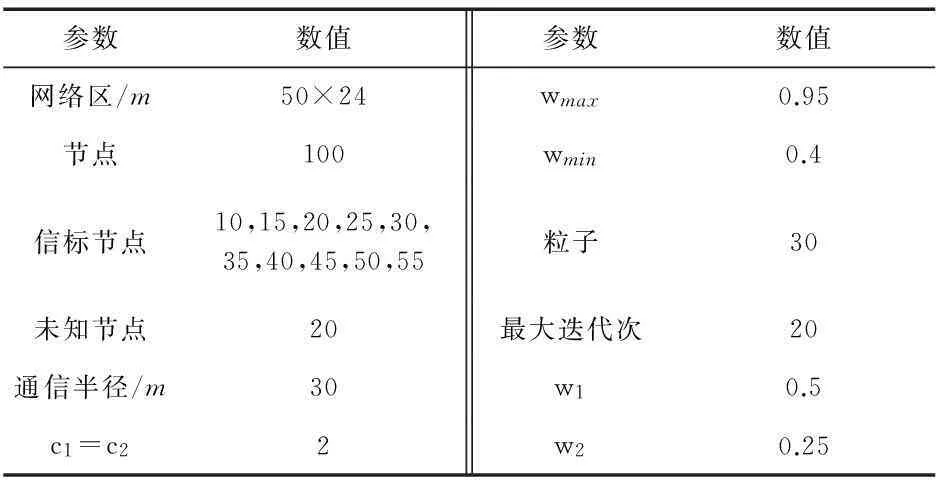
表1　仿真参数

3.2近邻点联合测距修正算法的误差分析

由图1和图2可知,在节点通信半径小或信标节点个数少的情况下，Nrt1测距修正的平均测距误差较低;反之,Nrt2测距修正的平均测距误差较低。为达到取长补短的效果，对测距修正系数做进一步的平衡改进。

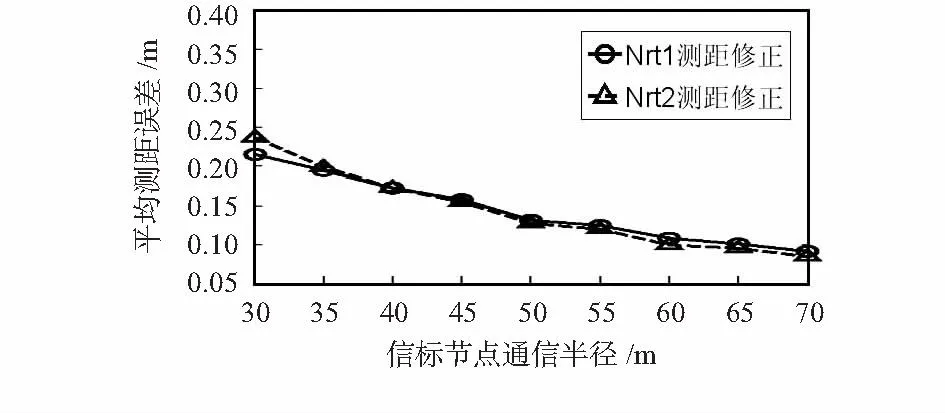
图1　平均测距误差与节点通信半径Fig 1　Average ranging error and communication radius of node

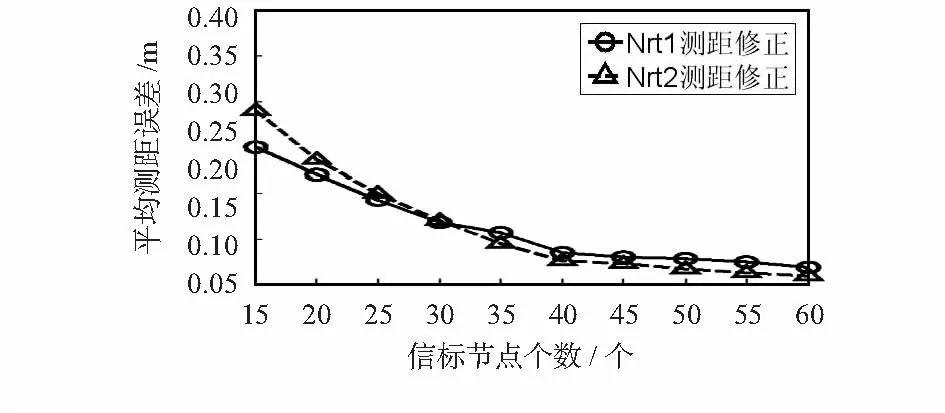
图2　平均测距误差与信标节点个数Fig 2　Average ranging error and beacon node number

通过联合Nrt1和Nrt2两种测距修正系数求和取平均值来进行改进，则测距修正系数统一为

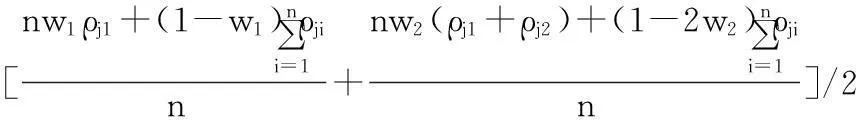
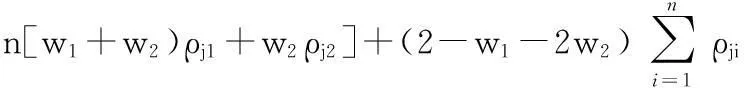
j>1

(12)

3.3实验结果分析

本文与测距差分修正算法WCLADC[12]和同类型的测距结合PSO的定位算法IPSO-IRSSI[8]进行比较。

由图3可以看出:在相同信标节点数下本文算法的定位误差明显小于WCLADC和IPSO-IRSSI算法，在相同定位精度下本文算法需要的信标节点数最少，可见本文算法更加充分的利用信标节点信息。

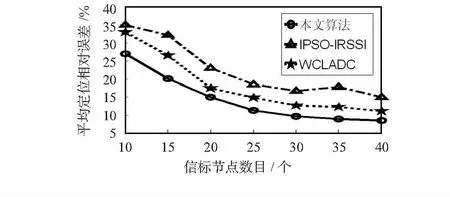
图3　本文算法与其它算法比较Fig 3　Comparison of algorithm of this paper with other algorithms

针对基于RSSI的测距会受环境影响的问题，由图4可以看出：随着平均测距误差的增大，平均定位误差也相应的增大，但本文算法对测距距离进行了比WCLADC更合理的修正，有效地降低了测距误差的影响，在相同的平均测距误差时本文算法的平均定位误差比其它算法降低了不少，尤其当测距误差较大时，本文算法的抗误差性更强。本文有效地解决了传统WCLADC算法测距修正的的局限性，实现了更加精准的修正。

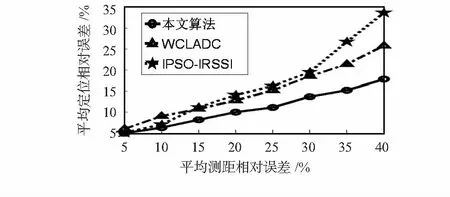
图4　测距误差对定位误差的影响Fig 4　Effect of ranging error on positioning error

图5描述了本文PSO与传统PSO算法的收敛特性。由该图可以明显看出：传统PSO需要迭代18次才能够收敛，相比较下，本文PSO收敛速度更快，迭代10次就可以达到收敛的效果，节约了能耗。

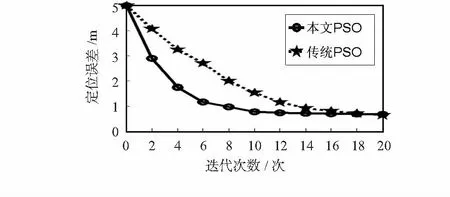
图5　本文PSO收敛特性Fig 5　Convergent characteristic of PSO of this paper

4　结束语

本文从理论原理和实验基础对传统差分修正算法进行了全面的分析，提出了一种近邻点联合测距修正PSO的定位算法来提高定位精度。通过上述仿真结果分析：本文定位算法没有额外的硬件要求和大幅的计算量，在定位精度等指标上比传统算法提高20 %，说明是符合设计要求的，对于节点随机分布的WSNs来说，该算法是一种更好的定位方案。

[1]DengZhongliang，YuYanpei，YuanXie.Situationanddevelopmenttendencyofindoorpositioning[J].ChinaCommunications，2013(3):42-55.

[2]BahlP,PadmanabhanVN.RADAR,aninbuildingonRF-baseduserlocationandtrackingsystem[C]∥IEEEComputerandCommunicationsSocietiesConference,2000:775-784.

[3]胡巧玲，提高基于WLAN的室内定位系统的适用性分析[J].华中科技大学学报,2013,41(2):197-200.

[4]关博,东超.立体式RSSI无线传感器网络定位算法[J].北华大学学报:自然科学版,2013,14(1):112-116.

[5]刘政.基于接收信号强度指示的误差自校正定位算法[J].传感技术学报,2014,27(7):970-975.

[6]蔡绍滨，高振国.带有罚函数的无线传感器网络粒子群定位算法[J].计算机研究与发展,2012,49(6):1228-1234.

[7]程伟，史浩山.基于差分修正的传感器网络传加权质心定位算法[J].系统仿真学报,2012,24(2):389-393.

[8]冯秀芳，吕淑芳.基于RSSI和分步粒子群算法的无线传感器网络定位算法[J].控制与决策,2014,29(11):1-7.

[9]KennedyJ,EberhartR.Particleswarmoptimization[C]∥IEEEInternationalConferenceonNeuralNetworks,Perth,1995:1942-1948.

[10] 王亚子，杨建辉.改进粒子群算法的无线传感器网络节点定位[J].计算机工程与应用,2014,50(18):99-102.

[11] 岳菲菲，关维国，邹德君，等.基于RSSI差分修正的WSNs定位算法[J]．辽宁工业大学学报:自然科学版,2012,3 (6):364-367．

[12] 花超,吉小军，蔡萍.基于RSSI差分修正的加权质心定位算法[J].传感器与微系统,2012,31(5):139-141.

PSO localization algorithm based on joint ranging modification of neighbor node*

WANG Zhe， LI Ping

(School of Computer and Telecommunications,Changsha University of Science and Technology,Changsha 410114,China)

Aimed at the problem that in the beacon nodes randomly distributed environment,reference node selection by traditional difference correction localization algorithm is too single,which cause that ranging modification coefficient has big error,propose a PSO localization algorithm based on joint ranging modification of neighbor node.The algorithm uses a joint ranging modification algorithm of neighbor node to get the modified distance from the unknown node to each beacon node,and then use an improved PSO algorithm to optimize the positioning result,obtain estimated position of unknown node.Simulation results show that the proposed algorithm has obvious improvement of positioning precision and achieve good stability,compared with traditional positioning algorithm.

wireless sensor networks(WSNs); neighbor node; RSSI; difference correction; particle swarm optimization(PSO)

2015—10—20

湖南省教育厅资助重点项目(14A004)

TP 212

A

1000—9787(2016)08—0130—04

王哲(1989-)，男，湖北黄冈人，硕士研究生，研究方向为无线传感器网络。

DOI:10.13873/J.1000—9787(2016)08—0130—04