改进的MIMO系统球译码检测算法*

仵　丹， 邵　朝

(西安邮电大学 通信与信息工程学院，陕西 西安 710121)



改进的MIMO系统球译码检测算法*

仵丹， 邵朝

(西安邮电大学 通信与信息工程学院，陕西 西安 710121)

针对球译码检测算法的搜索半径影响着其算法复杂度的问题，提出一种改进算法。改进算法对球译码检测算法的搜索半径乘上一个常量压缩因子，且在每层搜索中削减噪声因子的影响。通过缩减搜索球半径、缩小搜索范围实现算法复杂度的降低。仿真结果显示：在信噪比低于10 dB时，改进算法比传统球译码检测算法计算复杂度平均降低18 %左右，同时误码性能损失较小。

多输入多输出系统； 最大似然检测算法； 球译码检测算法； 改进算法

0　引　言

随着宽带多媒体无线通信数据业务的迅速发展和移动通信用户数量的急剧增加，用户对信息传输可靠性与数据传输速率的需求变得更高。多输入多输出(multiple-input multiple-output，MIMO)技术利用多个天线进行空时复用，能够在不增加系统带宽和发射功率开销的情况下，满足高速、可靠的通信及提高系统的频谱利用率[1]。因此，无线MIMO技术已经成为当代乃至未来无线移动通信发展中关键的技术之一[2]。随着MIMO技术的发展，对通信系统接收机的信号检测性能也提出了更高的要求，而系统接收机设计的目标在于使信号接收的差错概率尽可能的减小。目前，MIMO系统中经典的检测算法[3～5]主要有基于迫零(zero forcing，ZF)准则与最小均方误差(minimum mean square error，MMSE)准则的检测算法，QR分解算法，串行干扰消除(serial interference cancellation，SIC)算法，最大似然(maximum likelihood，ML)和球形译码(sphere decoding，SD)译码等算法。ML算法在发射向量先验等概率时，它等价于最大后验概率估计，因此,在这些检测算法中检测性能是最优的，但其算法复杂度与调制星座点数以及发送天线数目呈指数关系[6]。基于搜索格点的SD算法，可以在较低的计算复杂度下获得接近于ML算法的检测性能[7]。SD算法计算复杂度与其搜索半径有直接的关系，在最坏情况下仍然具有与ML检测算法相近的呈指数级增长的译码复杂度。

本文将介绍一种首先引入μ因子来约束SD算法在低信噪比时的搜索半径，然后结合噪声因子定义一种新的搜索半径，来实现对整个信噪比区间的搜索半径抑制的新方案。通过对ML算法，SD算法和改进算法进行性能和复杂度的分析仿真比较，来证实新算法可有效降低在低信噪比时的时间复杂度计算。

1　MIMO系统模型

在无线通信系统中，一个Nt根发射天线和Nr根接收天线的MIMO系统可表示为

y′=H′x′+n′

(1)

2　ML检测算法

ML检测的目标是在给定发射信号矢量x′和信道矩阵H′的条件下，从所有可能的发送信号集合中找出一个信号，使其满足

(2)

式中‖y′-H′x′‖2为ML检测的度量值，CNt为星座图中所有可能的星座点集合。

ML检测算法在误比特率最小的意义下是最优接收，理论上也可以证明它能获得最小的差错概率，但在检测时需要对星座空间中的所有发送信号点搜索一遍。因此，当发射天线数与调制阶数较高时，其计算量较大，在实际的多用户通信环境中难以应用，通常将它作为一个衡量其他译码算法性能的界限。

3　SD检测算法及其改进

3.1传统SD算法

SD检测算法，就是将ML检测的搜索空间限制在以接收矢量y′为球心，以c′为半径的球体内，来减少搜索信号点数，从而降低计算复杂度。SD通过调整球半径直到其内部存在一个ML解向量，当球体内部不存在解向量时增大半径，当球体内存在多个解向量时缩小球半径[8,9]。

复MIMO系统经过实部与虚部的分离可以转换成一个等价的实MIMO系统

y=Hx+n

(3)

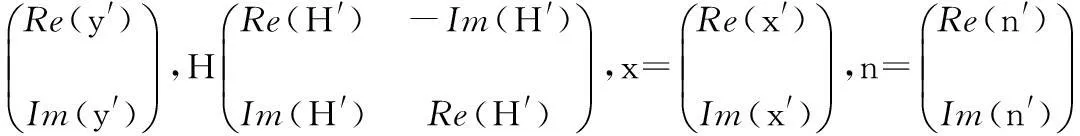
在实MIMO系统中，以接收矢量y为球心，以c为半径的球形译码算法可以表示为

‖y-Hx‖2≤c2

(4)

首先，对信道矩阵H进行QR分解，可以得到

(5)

式中(Q1Q2)为2Nr×2Nr的正交矩阵，Q1，Q2分别为2Nr×2Nt与2Nr×(2Nt-2Nt)的正交矩阵，R是2Nr×2Nt的上三角矩阵。依据正交矩阵不改变向量的范数的性质得

‖y-Hx‖2=‖QTy-QTHx‖2

(6)

(7)

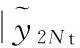
(8)

因此，可以获得

(9)

从而，可得到x2Nt的取值范围

(10)

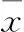
(11)

(12)

根据式(8)可以得到x2Nt-1的取值范围

(13)

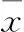
3.2改进SD算法

SD算法复杂度取决于访问信号点的数量和每个信号点的计算量，因此,可通过减少访问信号点数量或减少每个信号点的计算量来降低SD的复杂度。文中通过加快搜索半径的缩减，减少搜索范围中信号点数来降低SD算法复杂度。因此，在球形译码算法的研究中，球半径的选择是一个关键问题。

传统SD算法的搜索半径可以直接应用经验公式[10]

(14)

式中α使用经验值3，n为接收信号的维数，σ2为高斯白噪声方差，Γ()为伽马函数，ε为搜索不到信号点时的概率(一般取值为0.01)。

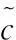
文中提出了一种改进的加快搜索半径缩减的算法。首先引入一个压缩因子μ乘以信噪比的式子来实现球半径的快速减小，其表达式为

(15)

式中参数c代表前一层的搜索半径，μ因子取值参考文献[12]。该算法称为基于μ因子的SD检测算法μ—SD，由表达式可以看出，信噪比不断降低时，球半径值趋于0，信噪比不断增大时，球半径趋于c2，因此,该算法对低信噪比时的搜索半径约束效果较好，而对高信噪比时的搜索半径约束效果较弱。

其次，根据式(3)，式(6)两式可得

(16)

(17)

由式(7)，式(8)两式可得

(18)

(19)

式中M是M2—QAM调制，由上式知，当i>1时，每一层搜索半径都受抑制，当i=1时，不适合抑制搜索半径。

4　仿真结果与分析

下面的仿真数据使用Matlab仿真环境，分别在2×2与4×4的MIMO系统统模型中采用16QAM和QPSK调制方式，仿真信道均为平坦衰落信道，信道中各元素独立同分布，服从均值为0，方差为1的复高斯随机变量。噪声采用加性高斯白噪声(AWGN)，且在接收端已知信道信息的情况下，对各种算法在不同信噪比时的误码率与算法时间复杂度进行了仿真比较。

图1、图3分别在不同调制方式与发送天线数下，对ML，传统SD，μ—SD及改进μ—SD算法的误码率性能进行比较，从图中可以看出ML，传统SD的误码率曲线几乎重合，说明SD算法能够实现接近ML的最佳检测效果。而μ—SD和改进μ—SD算法相对于传统SD算法牺牲了较小的误码率，但其检测性能依然十分接近传统SD的检测效果。

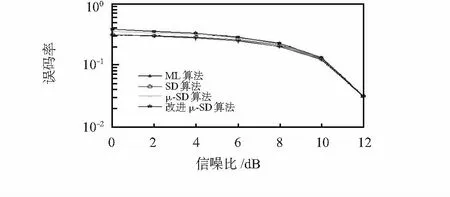
图1　2×2 16—QAM算法误码率比较Fig 1　Comparison of EBR of 2×2 16—QAM

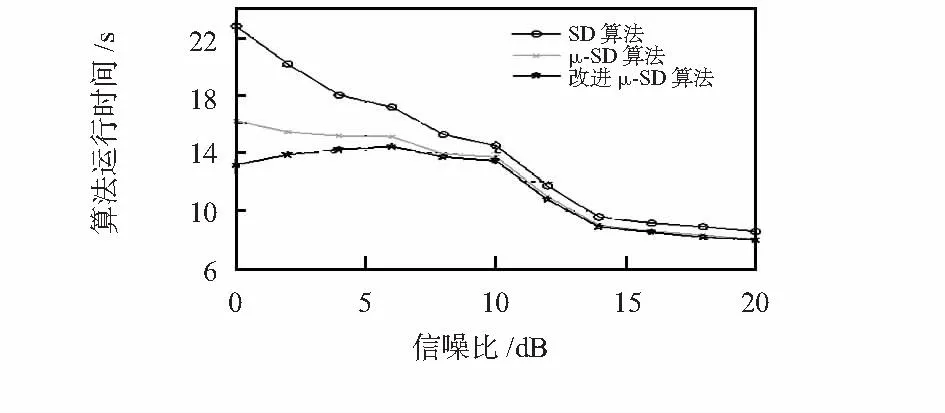
图2　2×2 16—QAM算法仿真时间比较Fig 2　Comparison of simulation time of 2×2 16—QAM

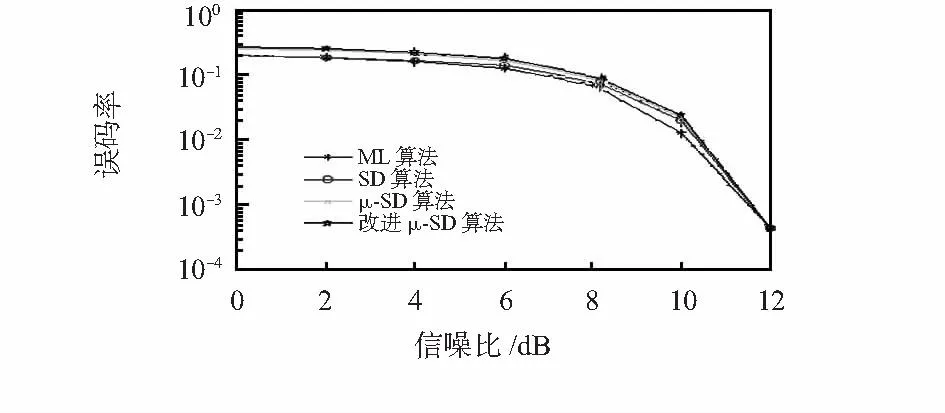
图3　4×4 QPSK算法误码率比较Fig 3　Comparison of EBR of 4×4 QPSK algorithm

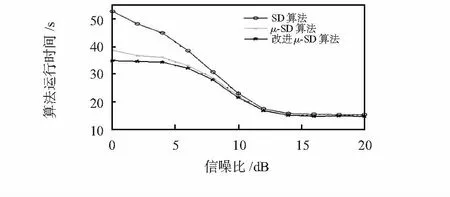
图4　4×4 QPSK算法仿真时间比较Fig 4　Comparison of EBR of 4×4 QPSK algorithm

图2和图4分别在不同调制方式与发送天线数下，对传统SD，μ—SD和改进μ—SD算法的计算时间复杂度进行比较，从图中可以看出，在低信噪比区域，球形译码具有较高的复杂度。μ—SD和改进μ—SD算法的计算时间复杂度在信噪比低于10 dB时，复杂度相比传统SD得到了一定的改善，改进μ—SD的算法计算时间平均降低了18 %左右。而在信噪比高于10 dB时，μ—SD和改进μ—SD算法的计算时间复杂度相对来说改善幅度较小。

综上，改进μ—SD算法的误码率性能在保持与传统SD算法性能相似的基础上，其计算时间复杂度在低信噪比时得到了有效改善，而在高信噪比时复杂度改善幅度较小。

5　结束语

针对球形译码复杂度较高的问题，文中引入了压缩因子与噪声因子相结合来抑制搜索半经，降低复杂度的改进算法。通过ML算法、SD算法、μ—SD算法和改进μ—SD算法的性能与复杂度比较，实验结果表明:改进算法在保持与传统算法相似的误码率性能下，可有效地降低球形译码算法在低信噪比时的计算复杂度。

[1]Nguyen V H,Berder O,Scalart P.On the efficiency of sphere decoding for linearly precoded MIMO systems[C]∥Wireless Communications and Networking Conference(WCNC),Shanghai:IEEE,2013:4021-4025.

[2]Ammu I,Deepa R.Performance analysis of decoding algorithms in multiple antenna systems[C]∥2011 the 3rd International Conference on Electronics Computer Technology(ICECT),Kanyakumari:IEEE,2011:258-262.

[3]岳珍梅,蔺俊杰,杜少波.一种改进的球形译码算法性能分析[J].兰州理工大学学报,2013,39(6):94-96.

[4]郑亮,卢建军,战金龙.V-BLAST检测算法性能研究[J].西安邮电学院学报,2011,16(4):1-4.

[5]刘毓,王国珍.垂直分层空时码检测算法性能分析[J].西安邮电学院学报,2012,17(1):18-21.

[6]王军选.多天线通信中的球译码技术[J].西安邮电学院学报,2006(11):43-46.

[7]Shariat-Yazdi R,Kwasniewski T.Low complexity sphere decoding algorithms[C]∥2008 IEEE International Symposium on Wireless Communication Systems,ReykjavIk,Iceland:IEEE,2008:438-442.

[8]Soltani M D,Alimadadi M,Amindavar H.A hybrid method to reduce the complexity of k-best sphere decoding algorithm[C]∥2014 the 22nd Iranian Conference on Electrical Engineering(ICEE),Tehran:IEEE,2014:1765-1770.

[9]Li Shiping,Wang Long,Chen Fangchao.Ordered sphere decoding detection algorithm for MIMO systems[C]∥Chinese Control and Decision Conference,2012:3322-3325.

[10] Viterbo E,Boutros J.A universal lattice code decoder for fading channels[J].IEEE Transactions on Information Theory,1999,45(5):1639-1642.

[11] Razavizadeh S M,VakiliI V T,Azmi P.A new faster sphere decoder for MIMO systems[C]∥Proceedings of the 3rd IEEE International Symposium on Signal Processing and Information Technology,Iran:IEEE,2003:86-89.

[12] 李世平,王隆.结合最小均方误差的改进球形译码检测算法[J].计算机应用,2012,32(2):385-387.

[13] 周曼,林云.一种基于统计裁剪的球形译码算法[J].广东通信技术,2013(5):72-76.

[14] Sonoda Y,Zhao H A.Improved sphere decoding algorithm with low complexity for MIMO systems[C]∥2014 IEEE/CIC International Conference on Communications in China(ICCC),Shanghai:IEEE,2014:11-15.

Improved sphere decoding detecting algorithm for MIMO*

WU Dan， SHAO Chao

(School of Communication and Information Engineering,Xi’an University of Posts and Telecommunications,Xi’an 710121,China)

Search radius of sphere decoding detection algorithm affects complexity of algorithm,an improved algorithm is proposed.The improved algorithm multiplies a constant compression factor on the search radius of the sphere decoding detection algorithm,and influence of noise factor is reduced in each layer.The complexity of the algorithm is reduced by cutting search radius of sphere and narrowing search range. Simulations results show that the new algorithm can effectively reduce calculation complexity by 18 % compared with the traditional sphere decoding detecting algorithm when signal to noise ratio(SNR)is less than 10 dB and cause the performance loss of bit error rate is small.

multiple-input multiple-output(MIMO)system; maximum likelihood(ML)detecting algorithm; sphere decoding(SD)detection algorithm; modified algorithm

2015—10—30

2014年国家“863”计划资助项目(2014AA01A705)；研究生创新基金资助项目(ZL2013—40)

TN 929.5

A

1000—9787(2016)08—0123—04

仵丹(1989-)，女，陕西宝鸡人，硕士，研究方向为通信信号处理及应用。

DOI:10.13873/J.1000—9787(2016)08—0123—04