利用递推增广矩阵辨识加速度计的参数

田　博， 韩峻峰， 郭毅锋， 杨　超， 李晶晶

(1.广西科技大学 电气与信息工程学院，广西 柳州 545006；2.钦州学院 机械与船舶工程学院，广西 钦州 535000)



利用递推增广矩阵辨识加速度计的参数

田博1， 韩峻峰2， 郭毅锋1， 杨超1， 李晶晶1

(1.广西科技大学 电气与信息工程学院，广西 柳州 545006；2.钦州学院 机械与船舶工程学院，广西 钦州 535000)

介绍了加速度计的基本工作原理和结构模型，将加速度计的微分方程转换成差分方程，在传统最小二乘法辨识的基础上，采用递推增广矩阵的辨识方法对加速度计的参数模型进行辨识。通过Matlab对其仿真，得到被辨识参数的估计值与曲线图，说明采用递推增广矩阵辨识方法辨识系统参数具有辨识速度快、辨识精度高、辨识结果准确等特点。

加速度计; 递推增广矩阵; 辨识; 仿真

0　引　言

加速度计作为一种敏感器件，在生活中被广泛运用于导航系统、游戏控制、制动检测、振动工程、地质勘测等领域，因此，它的参数辨识就显得尤为重要，传统的方法是采用最小二乘法[1～4]进行加速度计参数的辨识，这种最小二乘法一次就能完成算法的运算，适合于理论分析，但在实际的运用过程中，不仅占用内存大，通常用于离线辨识。

鉴于上述局限性，本文在最小二乘法基础上进行了改进，采用了递推增广矩阵法[5]进行加速度计参数的辨识，当辨识系统运行时，每取得一次新的观测数据后，就在前一次估计结果基础上，利用新引入的观测数据对前次估计结果根据递推算法进行修正，从而递推得出新的参数估计值。这样，随着新的观测数据逐次引入，依次进行参数估计，直到参数估计值达到满意的精度为止。这种递推增广矩阵法不仅快速、准确，占用内存小，扩充了维数，还能实时在线检测[6，7]。

1　加速度计的基本工作原理和结构模型

加速度计的基本工作原理为：所测量物理量在运动的过程中，根据经典的牛顿定律，会产生加速度，将运动加速度转化为惯性敏感元件相对于底座的运动的位移。

加速度计的结构模型：加速度计由弹簧[8]、基底和惯性敏感元件组成。弹簧的一端固定着基底，弹簧的另外一端连接着惯性敏感元件，形成一个振动系统。

加速度计的运动微分方程为

(1)

式中m为惯性敏感元件的质量；c为阻尼系数；k为弹簧的刚度系数；x为惯性敏感元件的位移。

2　递推增广矩阵的辨识方法

根据微分方程和差分方程的对应转化关系，加速度计模型转化成差分方程模型[9，10]如下

z(k)+a1z(k-1)+a2z(k-2)=b1u(k-1)+e(k)

(2)

式中z(k)为系统或者元件的输出量；u(k)为输入量；e(k)为测量误差。

在传统最小二乘法的基础上，采用递推增广矩阵的辨识方法来对该系统进行辨识，引入噪声模型v(k)，即有

e(k)=c(z-1)v(k)

(3)

加速度计采用递推增广矩阵辨识方法的一般框图如图1所示。

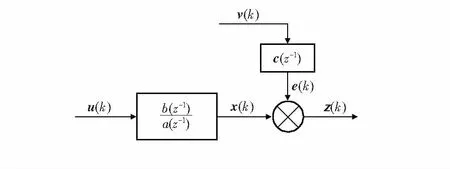
图1　采用递推增广矩阵辨识方法的框图Fig 1　Block diagram of identification method using recursive augmented matrix

对辨识系统进行参数赋值，有效位数取小数点后2位，得到精度较高的辨识。赋值之后便于Matlab仿真时真值与估计值有直观的对比。

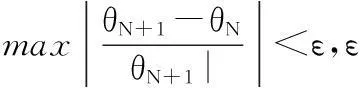
按照递推最小二乘法的形式可以得到递推增广矩阵

z(k)=hT(k)θ +v(k)

(4)

θ=[a1a2b1c1c2]

(5)

h(k)=[-z(k-1),-2(k-2),u(k-1),v(k),

v(k-1)]T

(6)

进而有递推增广矩阵

K(k)=P(k-1)h(k)[1+hT(k)P(k-1)h(k)]-1

(7)

P(k)=P(k-1)-k(k)hT(k)P(k-1)

(8)

(9)

3　仿真程序编程思路和仿真结果

3.1仿真程序编程思路

针对本系统参数辨识的需要，合理的选择4位移位寄存器产生的M序列来作为输入信号，且其长度为N=300，干扰信号是均值为0.64的不相关随机白噪声。

1)产生M序列输入信号和白噪声干扰信号;

2)绘出输入信号u(k)的图形和干扰信号白噪声v(k)的图形;

3)产生输出采样信号z(k);

4)被辨识参数θ(k)的估计值与残差的方差：

被辨识参数θ和p赋初值，设定初值如下

θ(0)=[0.0010.0010.0010.0010.001]T

(10)

(11)

根据递推增广矩阵法的递推公式求出k(k),p(k),θ(k),其中

K(k)=P(k-1)x(k)[1+hT(k)P(k-1)h(k)]-1

P(k)=P(k-1)-k(k)xT(k)P(k-1)

计算出辨识参数θ=[a1a1b1c1c1]的相对变化量及残差的大小。

5)判断是否满足收敛的条件；

6)显示被辨识参数；

7)绘制出待估参数的变化过程和残差；

8)结束。

3.2仿真结果

1)各个被辨识参数如图2所示。

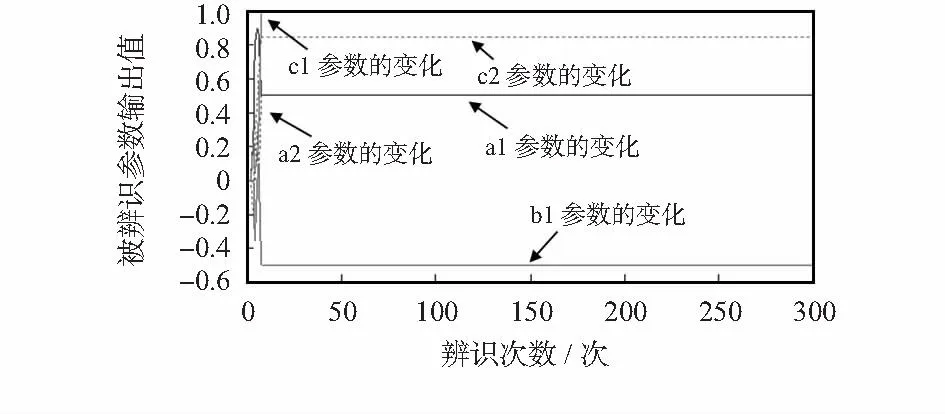
图2　各个被辨识参数Fig 2　Each parameter to be identified

2)各个被辨识参数收敛情况如图3所示。

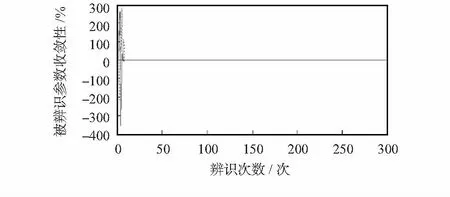
图3　各个被辨识参数收敛情况Fig 3　Convergence of each parameter to be identified

3)各个被辨识参数残差的方差与迭代次数的曲线图如图4所示。

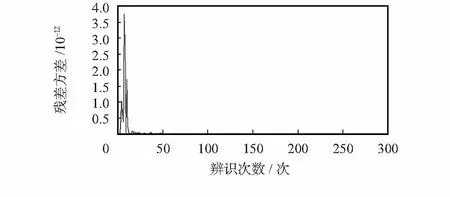
图4　残差的方差与迭代次数的曲线图Fig 4　Curve of residual variance and number of iterations

3.3试验结果列表和真值

递推增广矩阵法的被辨识参数试验结果与真值,Matlab仿真结果中截取的部分辨识参数的估计值如表1。

表1　Matlab仿真结果中截取的部分辨识参数的估计值

从表1可以看出:辨识次数仅到第7次时，被辨识参数就达到真值的结果，辨识速度快，在线辨识效果好；直到第300次时，被辨识参数仍然保持在真值的结果，辨识稳定性好，辨识结果准确。

根据辨识参数的真值和表1辨识参数的估计值，得到递推增广矩阵法被辨识参数试验结果与真值如表2。

表2　被辨识参数θ试验结果与真值

3.4结果分析

根据图2各个被辨识参数的图形可知：图形的横坐标表示的是辨识过程的次数N，纵坐标表示的是各个被辨识参数的结果。其中实线代表的是参数a1的变化过程，红色虚线代表的是参数a2的变化过程，蓝色实线代表的是b1的变化过程，绿色实线代表的是c1的变化过程，绿色虚线代表的是c2的变化过程。在这些参数曲线的初始辨识阶段，曲线的变化范围较大，但达到一定的辨识次数以后，系统辨识参数就各自趋近于一条直线，达到真值的结果，基本上达到了稳定的状态，满足了辨识的要求。图3表示的是各个被辨识参数收敛情况，当辨识参数的初始阶段时，各个参数的相对变化情况变化值较大，而当到了一定辨识次数，各个参数的相对变化为0，说明系统已经趋于稳定。根据图4残差的方差与迭代次数的曲线图可以看出，残差的方差随着辨识次数的增加先是曲线变化然后一直趋于一条直线达到稳定状态。

4　结束语

针对加速度计的数学模型，采用递推增广矩阵的辨识方法,不仅可以对模型的参数进行估计，还可以对噪声模型的白噪声干扰信号同时进行参数估计，只要合理调整辨识次数和辨识精度的取值，被辨识参数就能得到相对稳定的估计值。这种递推增广矩阵法具有辨识速度快，辨识精度高，辨识结果准确等特点。递推增广矩阵法还可以推广应用到辨识其他模型，与辅助模型相结合，可以辨识其他一些系统。

[1]肖昌润，刘洋，刘瑞杰.舰船模型试验用加速度计标定方法研究[J].传感器与微系统，2014,33(10):21-24.

[2]徐凤霞，夏刚，苏宝库，等.总体最小二乘辨识陀螺加速度计误差模型研究[J].传感器与微系统，2007,26(9)：20-22.

[3]陈剑,孙金海,李金海.惯性系统中加速度计标定方法研究[J].微电子学与计算机,2012,29(8):130-133.

[4]徐伟,李强,陈雪冬,等.基于小波降噪与最小二乘估计的石英挠性加速度计模型辨识[J].传感技术学报,2013,26(11):1493-1497.

[5]刘德军.基于系统辨识的控制系统设计[J].中山大学研究生学刊,2013,34(4):165-172.

[6]陆振先.基于递推最小二乘法的温箱系统辨识[J].工业控制计算机，2014,27(8):68-69.

[7]赵海森，杜中兰，刘晓芳，等.基于递推最小二乘法与模型参考自适应法的鼠笼式异步电机转子电阻在线辨识方法[J].中国电机工程学报，2014,34(30):5386-5394.

[8]李敏,刘俊，吕华溢，等.一种新型四维加速度传感器研究[J].传感器与微系统，2014,33(3):48-51.

[9]易伟健，刘翔.动力系统模型阶次确定[J].振动与冲击，2008，27(11):12-16.

[10] 盛晓婷.模型阶次辨识[J].振动与冲击，2009，28(11):32-33.

Identification of parameters of accelerometer based on recursive augmented matrix

TIAN Bo1， HAN Jun-feng2, GUO Yi-feng1, YANG Chao1, LI Jing-jing1

(1.School of Electrical and Information Engineering,Guangxi University of Science and Technology，Liuzhou 545006,China;2.College of Mechanical and Marine Engineering，Qinzhou College，Qinzhou 535000,China)

Basic working principle and structure model of accelerometer is introduced,and then differential equations of accelerometer is converted to difference equation,on the basis of traditional least squares method identification,using identification method of recursive augmented matrix,parameters model of accelerometer are identified.Identification simulation is carried out by Matlab,parameter estimation value and curve graph is obtained,it shows that using recursive augmented matrix identification methods to identify system parameter identification has advantages of fast speed,high identification,accurate identification results,and so on.

accelerometer ;recursive augmented matrix; identification; simulation

2015—11—06

TH 824

A

1000—9787(2016)08—0051—03

田博(1988-),男,湖北应城人,硕士研究生,研究方向为汽车电子控制技术。

DOI:10.13873/J.1000—9787(2016)08—0051—03