三轴一体石英挠性加速度计标定数学建模与误差分析*

赵桂玲， 郭文婧， 李　松

(辽宁工程技术大学 测绘与地理科学学院，辽宁 阜新 123000)



三轴一体石英挠性加速度计标定数学建模与误差分析*

赵桂玲， 郭文婧， 李松

(辽宁工程技术大学 测绘与地理科学学院，辽宁 阜新 123000)

为了提高加速度计标定精度，针对三轴一体石英挠性加速度计确定性误差特性和工程安装特点，基于笛卡尔空间坐标系之间的转换，推导加速度计坐标系与载体坐标系之间的转换矩阵，建立三种石英挠性加速度计线性标定数学模型。仿真和导航实验结果表明：三轴一体石英挠性加速度计标定数学模型误差引起捷联惯性导航系统速度误差、位置误差和姿态误差，且姿态误差和位置误差包含常值分量；所有误差均包含舒勒周期振荡和傅科周期振荡，傅科周期振荡调节舒勒周期振荡。

石英挠性加速度计； 标定； 数学建模； 导航

0　引　言

石英挠性加速度计以其结构简单、精度和灵敏度高、稳定性好、性/价比高等优点在航空、航天、航海、石油、测绘等领域得到快速发展和广泛应用[1～4]。将加速度计安装到惯性测量单元(inertial measurement unit，IMU)基座上时，由于基座支架加工的垂直度误差以及加速度计实际输入轴与理想输入轴之间存在的失准角误差，使得加速度计实际输入轴组成的坐标系是一个非直角坐标系，然而加速度提供给惯导系统进行解算的数据应该是在统一直角坐标系下表示的比力矢量[5]。为了实现从非直角坐标系到直角坐标系的测量转换，必须在单个加速度计元件级测试之后再进行三轴一体加速度计的组合级标定与补偿。三轴一体加速度计标定模型分为线性模型、二次非线性模型、考虑失准角的模型、考虑杆臂的模型和考虑动态误差的模型等。从补偿精度和标定实验难度出发，三轴一体石英挠性加速度计应用最多和最方便的是线性模型。石英挠性加速度计标定采用的线性数学模型主要集中在为3个安装误差角、6个安装误差角和9个安装误差角等几种形式[6～10]。

无论石英挠性加速度计标定误差模型采用何种形式，研究热点主要集中于采用何种标定方法对石英挠性加速度计进行精确标定，鲜有对标定模型本身精确性和适用性的分析与研究。针对石英挠性加速度计线性标定误差模型建立不够精确、模型过于简化不能满足精度要求、模型参数过多给标定带来一定困难等关键工程应用问题，以三轴一体石英挠性加速度计安装误差角为切入点，提出一种基于空间笛卡尔坐标系转换的石英挠性加速度计线性标定误差建模方法，并给出模型中各个参数的物理含义和模型的适用条件。

1　加速度计标定线性建模

单个石英挠性加速度计静态输入输出标定数学模型为

Nm=Kmfm+Am0,m=x,y,z

(1)

式中Nm为加速度计的脉冲输出，fm为加速度计比力，Km为加速度计标度因数，Am0为加速度计零偏。将三轴一体石英挠性加速度计模型合在一起写成矢量的形式

(2)

式中

Na=[NxNyNz]T

Ka=diag[KxKyKz]T

fa=[fxfyfz]T

(3)

式中fa为比力矢量在加速度计坐标系(oa-xayaza,a系)下的投影，而惯性导航解算需要的是比力矢量在载体坐标系(ob-xbybzb，b系)下的投影fb，fb与fa之间存在如下关系

(4)

(5)

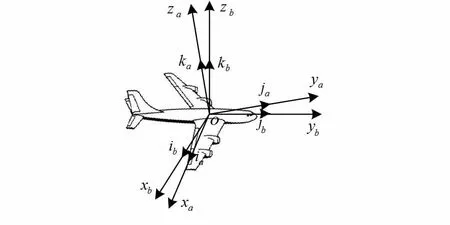
图1　坐标系安装示意图Fig 1　Diagram of coordinate system installation

ia,ja,ka表示a系轴向的单位矢量，ib,jb,kb表示b系轴向的单位矢量，b系到a系的基变换公式为

(6)

b系到a系的坐标变换矩阵

(7)

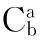
简化一：加速度计输入轴与载体坐标系b系对应轴成小角度安装

cosθmanb≈1,m=n=i,j,k

cosθmanb≈π/2-θmanb,m≠n;m,n=i,j,k

(8)

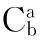
(9)

简化二：加速度计输入轴与载体坐标系b系对应轴成小角度安装，且三个轴正交安装

cosθmanb≈1,m=n=i,j,k

(5) 各指标主、客观权重最优组合。根据式(12)～(17)可以求出上述主观权重Wz，Wc和客观权重Wb，Ws的重要程度系数α=0.518，β=0.482，根据主、客观权重的重要性系数，最终可得各指标主、客观权重的组合向量W={0.332，0.102，0.124，0.085，0.105，0.062，0.190}。

cosθmanb=-cosθnamb,m≠n;m,n=i,j,k

(10)

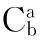
(11)

3　六位置分立式标定

为了验证加速度计标定模型的正确性和标定模型误差对导航结果的影响，设计六位置标定路径对三轴一体加速度计进行标定，设计的加速度计标定路径如图2所示。

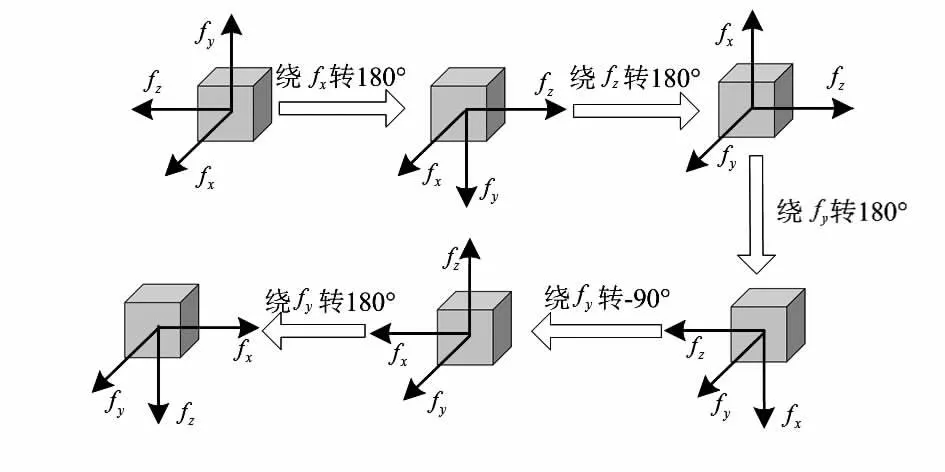
图2　六位置标定路径Fig 2　Path of six positions calibration

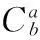
(12)

将式(12)代入式(5)，可得三轴一体加速度计静态输入输出标定数学模型为

(13)

六个位置的加速度计脉冲输出如表1。

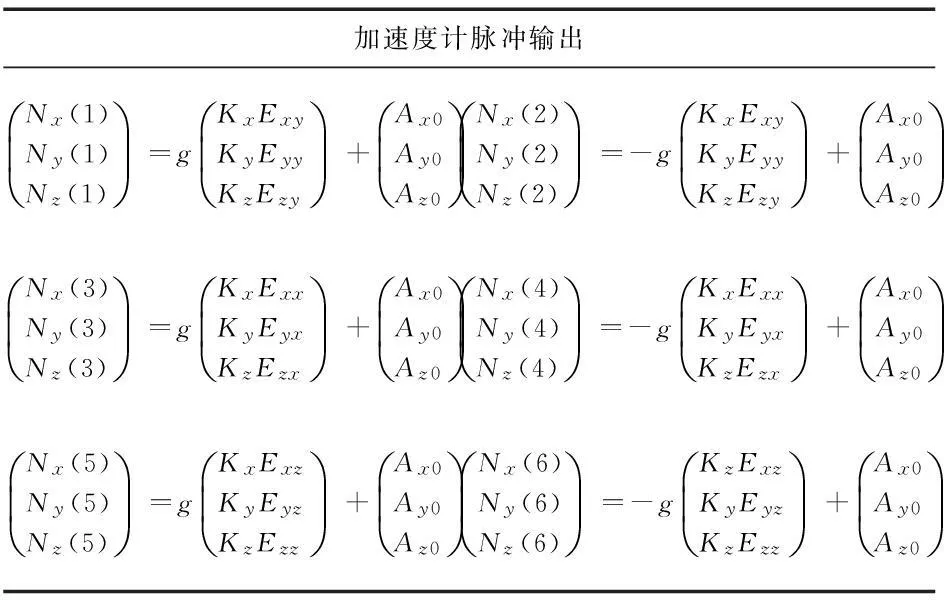
表1　加速度计脉冲输出

根据六个位置的加速度计脉冲输出，可以计算出加速度计的输入输出模型参数

(14)

(15)

(16)

(17)

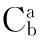
(18)

(19)

采用简化模型的加速度计脉冲输出在六个位置如表2。

表2　简化模型下的加速度计脉冲输出

根据表2的加速度计脉冲输出，可以计算速度计标定简化模型的零位和标度因数

(20)

(21)

采用简化模型一的三轴一体加速度计数学模型中的安装误差为

(22)

采用简化模型二的三轴一体加速度计数学模型中的安装误差为

(23)

将式(14)～式(17)、式(20)～式(23)计算出的加速度计标定参数分别代入式 (13)、 式(18)和式(19)，则可以根据任意加速度的脉冲输出计算加速计的输入比力fb。

4　模型误差对导航的影响

4.1计算机仿真

采用六位置分立式标定方法对三轴一体石英挠性加速度计进行仿真和实验，这里只分析简化模型误差对导航的影响。其中标度因数、安装误差和零位分别在700±10，±0.1°和20±5随机产生。简化的加速度计标定数学模型对导航的影响如图3～图8所示。

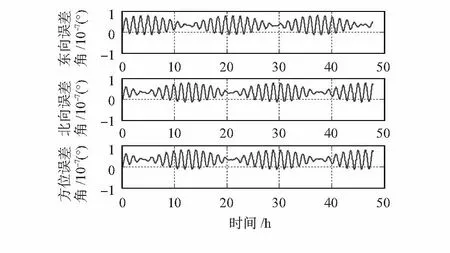
图3　简化模型一对姿态的影响Fig 3　Influence of simplified model 1 on attitude

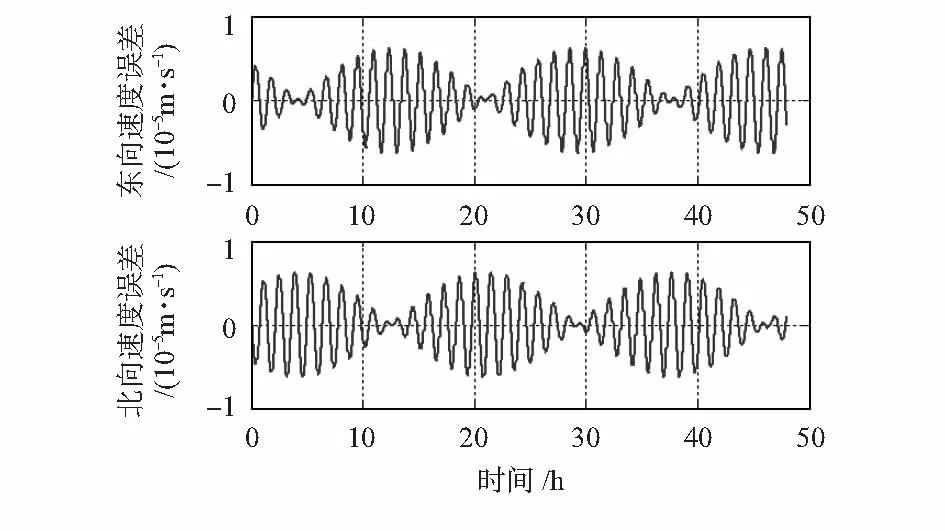
图4　简化模型一对速度的影响Fig 4　Influence of simplified model 1 on velocity

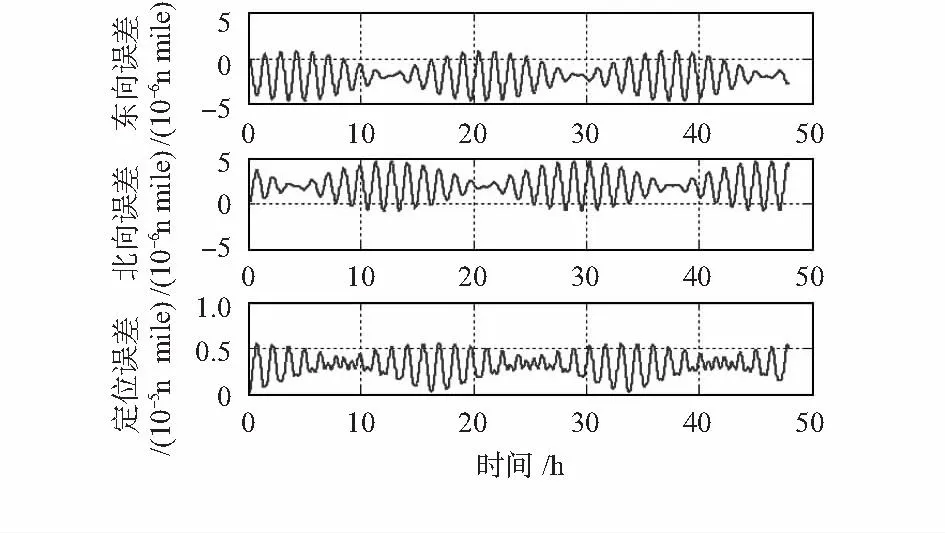
图5　简化模型一对位置的影响Fig 5　Influence of simplified model 1on position

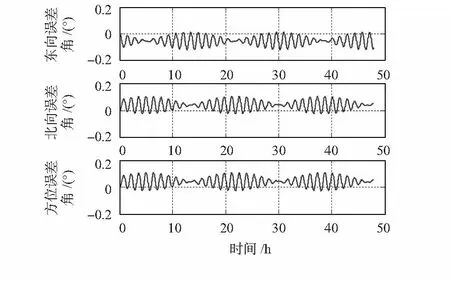
图6　简化模型二对姿态的影响Fig 6　Influence of simplified model 2 on attitude

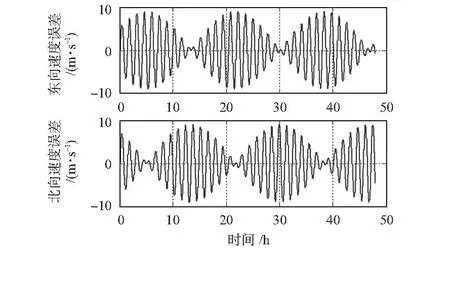
图7　简化模型二对速度的影响Fig 7　Influence of simplified model 2 on velocity

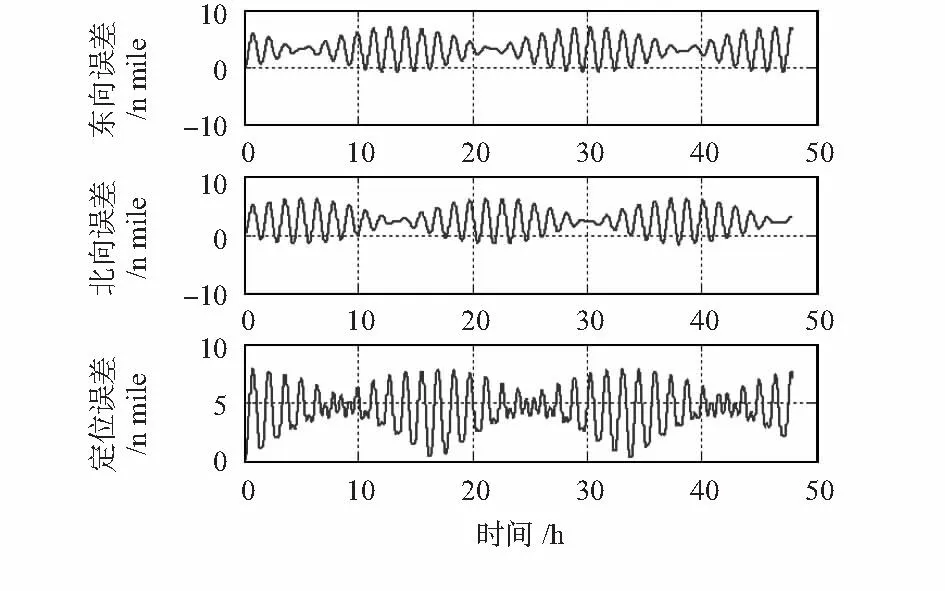
图8　简化模型二对位置的影响Fig 8　Influence of simplified model 2 on position

从仿真图可以看出：在此仿真条件下，简化的三轴一体石英挠性加速度计标定数学模型误差引起惯导系统速度误差、位置误差和姿态误差。在7个导航参数误差中，傅科周期振荡调制舒勒周期振荡，且加速度计标定简化数学模型误差引起姿态误差和位置误差的常值分量。

4.2标定与导航实验

将石英挠性加速度计和光纤陀螺组成的捷联惯性导航系统置于三轴惯性测试转台(角位置精度为3″)并预热30 min，按照式(13)、式(18)、式(19)三种标定数学模型分别进行加速度计标定，并将标定结果代入系统进行静态导航实验，前13.5 h进行对准估漂，导航结果如图9所示。采用9个安装误差角、6个安装误差角和3个安装误差角形式的三轴一体加速度计标定误差模型60 h静态定位误差分别为4.76,5.03,15.88 n mile。采用9个安装误差角形式的导航结果与简化为6个安装误差角形式的导航结果精度相当，其定位误差远远小于简化为3个安装误差角形式的定位误差。这是因为6个安装误差角形式的简化模型误差引起的导航误差相对于初始对准、加速度计漂移、转台误差等引起的导航误差，可忽略不计。

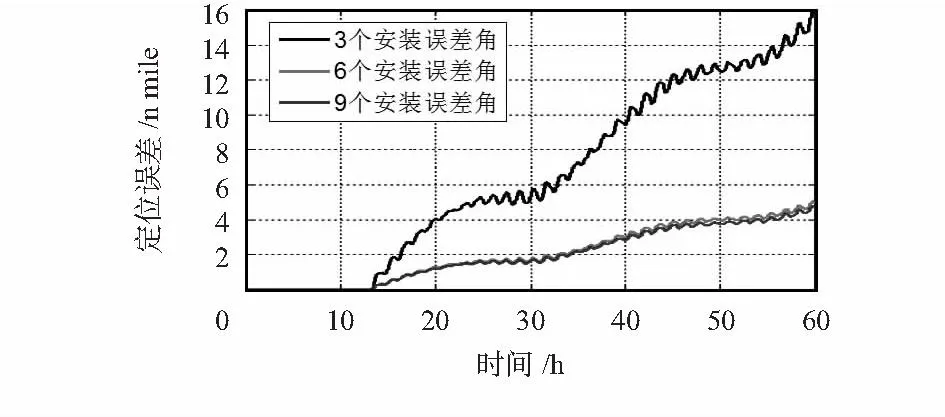
图9　捷联惯性导航系统定位误差Fig 9　Positioning errors of strapdown inertial navigation system

5　结　论

利用空间笛卡尔坐标系变换，推导三种加速度计标定数学模型，并设计六位置标定路径分别对三种模型进行仿真和实验验证，得到以下结论：1)简化的加速度计标定数学模型误差引起系统速度误差、位置误差和姿态误差，且姿态误差和位置误差均包含常值分量。2)导航实验中的定位误差远远大于仿真结果，这是因为在标定和导航实验中，不可避免地会存在陀螺误差、转台定位误差、初始对准误差等对导航结果的影响。综合补偿效果和标定实验的难度，对于导航级的捷联惯性导航系统，6个安装误差角形式的三轴一体加速度计标数学模型是一个较为理想的选择。

[1]张晞,张声艳,顾欣怡,等.数字闭环石英挠性加速度计表头离散化研究[J].传感器与微系统,2012,31(12):62-65.

[2]朱海燕，叶凌云，彭皓岚，等.石英绕性加速度计数字闭环控制研究[J].传感器与微系统,2015,34(8):61-63.

[3]王勇,唐光庆,周静梅,等.石英挠性加速度计磁路仿真分析与优化设计[J].压电与声光,2010,32(4):551-557.

[4]刘艳霞,方建军,杨清梅.基于椭球假设的三轴加速度计误差标定与补偿[J].传感器与微系统,2014,33(6):52-64.

[5]严恭敏,李四海,秦永元,等.惯性仪器测试与数据分析[M].北京:国防工业出版社,2012:196-222.

[6]程骏超,房建成,吴伟仁,等.一种激光陀螺惯性测量单元混合标定方法[J].中国惯性技术学报,2014,22(4):445-452.

[7]Song Ningfang,Cai Qingzhong,Yang Gongliu,et al.Analysis and calibration of the mounting errors between inertial measurement unit and turntable in dual-axis rotational inertial navigation system[J]. Measurement Science and Technology,2013,10:1-10.

[8]张华强,赵剡,陈雨.捷联惯性导航系统整体标定新方法[J].北京航空航天大学学报,2012,38(4):459-463.

[9]Kim Moon-Sik,Yu Si-Bok,Lee Kwang-Soo. Development of a high-precision calibration method for inertial measurement unit[J]. Inernational Journal of Precision Engneering and Manufacturing,2014,15(3):567-575.

[10] 程耀强,徐德民,万彦辉,等.斜装激光陀螺石英加速度计标定算法研究[J].压电与声光,2013,35(3):362-367.

赵桂玲(1983-)，河北沧州人，博士，讲师，研究方向为惯性导航系统标定与初始对准技术。

Mathematical modeling for calibration of three-axis integration quartz flexible accelerometer and error analysis*

ZHAO Gui-ling, GUO Wen-jing, LI Song

( School of Geomatics,Liaoning Technical University,Fuxin 123000,China)

In order to improve precision of accelerometer calibration,aiming at certainty error characteristics and engineering installation features of three-axis integration quartz flexible accelerometer,derived and researched, the transformation matrix between accelerometer coordinate system and carrier coordinate system based on transformation of Cartesian coordinate system is deduced. Three quartz flexible accelerometers calibration mathe-matical models is established.Simulations and navigation experimental result shows that on static conditions error of calibration mathematical model cause velocity error,position error and attitude error; and attitude error and position error contain constant component;all errors contain Schuler Periodic shocks and Foucault Periodic shocks. Foucault Periodic shocks modulate Schuler Periodic shocks.

quartz flexible accelerometer; calibration; mathematical modeling; navigation

2015—10—26

国家自然科学基金资助项目(41404035)；导航位置服务国家测绘地理信息局重点实验室开放基金资助项目(2013NL002)

U 666.1

A

1000—9787(2016)08—0015—05

DOI:10.13873/J.1000—9787(2016)08—0015—05