城市突发事件下的应急物资配送路径寻优

王付宇，叶春明，王涛（.安徽工业大学管理科学与工程学院，安徽马鞍山4303；.上海理工大学管理学院，上海00093）

城市突发事件下的应急物资配送路径寻优

王付宇1，2，叶春明2，王涛1
（1.安徽工业大学管理科学与工程学院，安徽马鞍山243032；2.上海理工大学管理学院，上海200093）

针对城市突发事件环境下的应急物资配送车辆行驶路径寻优问题，分析城市道路拥堵状况对于救援车辆行驶速度的影响。以车辆到达待救点的时间和行驶成本最少为目标，构建双层规划路径寻优模型。为提高全局搜索和局部寻优能力，采用一种改进的两阶段式萤火虫算法。算例结果表明所提出的模型和算法可有效解决城市突发事件下的应急物资配送问题。

应急救援；路径寻优；双层理论；萤火虫算法

近年来，除了地震、洪涝等大规模自然灾害频发，城市内部公共突发性事件也层出不穷，其带来的生命威胁与财产损失不可忽视。此类城市范围内突发性事件的救援工作对于救援响应时间和救援时间周期的紧迫性更加严格。然而城市区域内复杂的路网和时变的路况对于救援车辆行驶速度有着明显的影响。因此，为了确保城市发生各种突发事件后城市应急救援中心能够及时响应、选择最佳救援路线、实施高效救援，面向城市交通复杂路况下的应急物资配送路径寻优已成为目前亟待解决的问题［1-2］。

目前，国内外学者就应急救援物资配送路径问题作了大量研究。Dantzig等［3］于1959年提出车辆路径问题，并指出该问题本质上属于运筹学与组合优化领域。Balcik等［4］针对灾害后不确定信息下的救援和物资配送进行研究，以总成本最小为目标，建立了从供应点到资源需求点的多物品网络流模型。Ceyhun［5］研究基于救援中心属于覆盖模型环境下的车辆路径寻优问题，为使得每台救援车辆能够高效地服务更多的待救点，建立了一种多目标车辆路径寻优模型。Pretolani［6］分析某城市路段行驶时间的结果分布规律，总结出该城市路段行驶时间呈正态分布，该结果对应急救援车辆行驶速度的判定有着很大启发作用。马祖军等［7-8］对洪灾地震等自然灾害和城市公共突发事件下的应急救援中心的选址及车辆路径寻优问题进行研究，提出应急物资配送中心定位与配送车辆路径安排的联合决策问题，对此建立了模糊多目标定位及路径寻优模型。乔茹等［9］基于改进蚁群算法研究移动机器人全局路径规划问题。姜金贵等［10］针对城市内涝突发情况下，引用连通系数和畅通系数来计算车行速度，从而反映出道路积水阻碍交通等影响因素，建立相应的救援路径寻优模型，以提高救援效率降低灾害损失。在求解方法上，Purezza等［11］运用禁忌搜索算法求解车辆优化调度的问题；Torki等［12］提出用自组织的神经网络算法来求解车辆路线优化问题；宋晓宇等［13］用遗传算法求解了灰色规划模型，通过测试种群数目、交叉率和变异率3种控制参数值以提高算法性能。

上述有关应急救援车辆路径寻优研究中，仅仅采用1-0决策判断方法处理道路是否能够通行，而忽略了城市本身道路交通拥堵特征。其中采用的多目标路径寻优模型在建立目标函数时，大多是采用权重分配的方法处理时间最短和成本最低多目标之间的关系，而该方法所得出的结果容易忽略应急救援过程中的及时性，即使时间的权重比较大，也会出现结果偏向于所耗时间和成本较小的可能。在求解方法上基本采取智能启发式算法，对于群体智能算法的应用相对不够成熟。基于此，本文针对城市车辆行驶速度特征进行分析，提出道路拥挤条件下的双层路径寻优模型，并构建混沌萤火虫算法进行求解。

1　路径寻优模型

1.1问题描述

传统物流配送车辆路径寻优问题，是在物流配送中心以及物资需求点坐标位置、道路交通状况、需求点物资需求量等因素已知的基础上进行的。而应急救援车辆路径规划的过程中，救援需求点位置的随机性、道路修复状况、时变下的道路拥堵信息等不确定因素使得该情景下的车辆路径寻优问题变得异常复杂。对应急救援路径选择问题的描述如下：选择车辆行驶时间最短以及车辆运输成本最少作为目标。系统中只有一个救援配送中心，且地理坐标位置及所拥有的救援车型、数量、单车容量已知，救援中心派出车辆对多个待救点进行服务，完成物资配送后返回救援中心。

车辆行驶过程中应满足以下几个假设条件：

1）道路节点之间有可行通路；

2）每个待救点只能接受一辆车一次救援；

3）每辆车在一次救援巡回过程中的载重不能超过其最大容量；

4）车辆行驶速度小于等于其最大限制行驶速度。

以城市交通路网作为建立应急救援车辆最优路径模型基础，节点（待救点）与节点之间的路线设定为一条弧段。应急救援车辆路径问题可以用图论形式表示出来：记G（I,L）为赋权图，I为顶点集，L为边集，定义决策变量如下：

其中：i，j表示待救点序号，i，j=0，1，…，m；k代表派使的第k台救援车辆，k=1，2，…，K；其中i，j=0，表示救援中心。式（1），（2）为决策变量，判断救援车辆是否通过i和j节点，以及节点i是否被第k辆救援车所提供服务。

1.2数学模型

双层路径寻优模型不同于以往的多目标路径寻优模型［14］。多目标模型一般是以车辆行驶路径最短、成本最低、时间最短等作为目标，并且诸多目标之间以设定权值综合考虑。而双层路径寻优模型更加强调突发事件发生后对应急物资配送的及时性，该模型以应急救援物资配送车辆行驶总时间最短为主要优化目标，在充分体现及时性的基础上再以车辆行驶所耗总成本最低为辅助目标，从而使救援中心位置能够及时服务于待救点伤员并且尽量降低救援车辆所耗成本。双层路径寻优数学模型表达如下：

目标函数：

其中：

约束条件：

其中：（x0，y0）表示救援中心位置；（xi，yi）表示待救点位置；di表示各待救点对该物资的需求量；D表示每辆救援车的最大容量；ck表示第k辆车，每行驶单位距离所消耗的成本；lij表示i与j之间距离；vij表示车辆行驶于i与j之间的速度；τij表示车辆行驶于i与j之间所耗时间；vˉ表示车辆的平均速度；vmax表示车辆的最大速度；qij表示i与j之间道路的畅通度；pij表示i与j之间道路的最大通行量。式（5）引入最大速度和平均速度，当路径畅通度与路容量以及平均速度的乘积小于最大速度时，则实际速度为三者之积；反之，速度则控制在最大速度，不允许超速；式（3），（4）分别为应急物资配送车辆行驶时间和所耗成本优化函数；式（7），（8）表示每个待救点均得到车辆救助，并且每个待救点只出现在一台救援车辆的路径上；式（9）保证每台救援车辆历经的所有待救点的总需求量小于该车最大容量；式（10）～（12）保证每一台车辆能够形成可行回路。

2　算法设计

2.1混沌萤火虫算法思路

在标准萤火虫算法的基础上引入惯性权重，使算法的全局搜索和局部寻优能力得到一定改善。但是，实验发现，一旦达到局部极值点附近，算法收敛速率慢，且在极值点附近振荡；对于一些多峰多极值点问题，算法仍存在陷入局部最优问题。混沌运动具有遍历性、随机性等特点，为此，本文在萤火虫算法的基础上引入混沌思想，从而提高萤火虫种群的多样性和寻优的遍历性，增加算法摆脱陷入局部极值点的能力。改进后的混沌萤火虫算法是利用载波的方式，将混沌变量映射到萤火虫优化算法的搜索空间，再利用混沌变量进行搜索寻优［16］。搜索的过程分为2个阶段。

1）粗略搜索

为提高算法收敛速度，在迭代运算初期，利用基于惯性权重的萤火虫算法进行大范围全局搜索，寻找整个搜索空间中的满意极值点。

2）细致搜索

选取粗略搜索法所得适应度高的10%至20%萤火虫，结合混沌映射再进行局部搜索，在粗略搜索的极值点附近寻找出全局下最优解。

2.2混沌萤火虫算法求解步骤

改进混沌萤火虫算法流程如下。

1）系统初始化，生成萤火虫初始种群的规模、位置信息（Xa（t）），设置光强吸收系数（γ）、最大吸引度（β0）和步长因子（α）等参数。

2）计算群体中每个萤火虫的荧光亮度，

其中I0表示萤火虫的最大荧光亮度，即自身r=0处。

3）对所有萤火虫个体进行邻域搜索，此时的搜索半径最大，并且计算出邻域中所有候选萤火虫个体的吸引度，

4）根据式（15），（16）更新萤火虫位置，最亮的萤火虫个体随机移动，

其中：t表示迭代次数；tmax表示最大迭代次数；ω（t）表示惯性权重；ωmax,ωmin表示最大、最小权重。

5）在有限的迭代次数内，通过以上步骤可以得出一组萤火虫亮度数据，从中选取萤火虫种群中适应度高的20%个体，进行混沌局部搜索。

6）将萤火虫位置信息Xbt按下式映射为0到1之间的混沌参量C（Xbt），

其中Xmax s和Xmin s分别为搜索空间中s维的上界和下界（假设萤火虫的位置空间为s维，当s=1时，Xmaxs=Xmax，Xmins=Xmin）。

7）当迭代次数t=t+1时，根据式（17）计算得到下步迭代的混沌参量，并将混沌参量）按式（18）映射转化为Xt+1b，

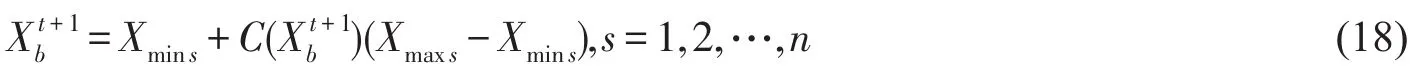
8）候选萤火虫个体适应度值大于当前萤火虫的适应度值，则替换当前萤火虫个体，实现萤火虫对较优个体位置的移动。

9）按下式收缩搜索区域

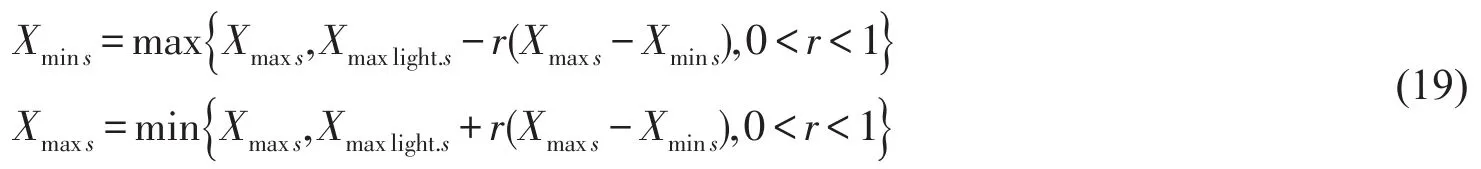
其中Xmaxlight.s表示当前最亮萤火虫个体的第s维变量的值。

10）若混沌搜索已到预先设定的精度或迭代次数，则将新解作为算法的最终结果，否则令t=t+1并返回步骤6）。

3　算例

3.1算例背景

某城市道路车辆行驶速度一般在20 km/h左右，但是在高峰期时段内，由于车流量过大导致车速受到严重影响。由该城市道路交通部门的车辆行驶监控资料分析路网拥堵状况，道路畅通系数取值于0.5～1.0，道路交通容量取值范围2～4，根据抽检的车辆速度计算得该城市内车辆行驶的最大速度为9.6 km/h、平均速度为3.6 km/h。另外，该城市大多数道路为东西和南北方向，为了方便理解在求解过程中直接取绝对值距离。

取应急救援中心周围长宽均为10 km区域为研究范围，设待救点的坐标为（xi，yi），根据该城市历史突发事件相关数据，救援中心（5，5）和待救点具体数据如表1所示。此外假设，应急物资配送车辆最大的容量为10 t，车辆行驶1 km所耗成本为5元。

以该城市路网拥堵环境下的应急物资配送问题为研究对象，优化目标是在应急物资配送车辆总行驶时间（T）可以接受的范围内（［Tmin，Tmin（1%+2%）］）使得车辆行驶成本最低。

表1　需求点坐标及需求量Tab.1 Demand Point CoordinateAnd Demand

3.2算例求解

1）参数设定

在Matlab环境下建立相关数据库，其中包括救援中心及待救点坐标（xi，yi）、各待救点的物资需求量（di）、车辆数目（K）、车辆k行驶单位距离消耗成本（ck）、单车最大容量（D）、车辆平均速度）、最大速度（vmax）、待救点间距离（lij）。另外，随机产生21×21组道路畅通系数和通行容量（pij，qij）。该案例涉及的救援中心及待救点地理分布如图1所示。萤火虫算法求解参数设定为萤火虫数m=10，光强吸收系数γ= 1.0，最大吸引度 β0=1.0，步长因子α=0.2，迭代次数tmax=200，ωmax=1，ωmin=0.4。

图1　需求点分布Fig.1 Demand Point Distribution

2）初始路径方案

根据最近邻域法得出第一个车辆行驶路径方案，共派出3辆应急物资配送车辆，第1辆共载重为9.3 t，行驶22 km，路径为0-2-3-4-5-20-7-6-0；第2辆共载重为9.0 t，行驶24.4 km，路径为0-16-9-19-14-8-10-1-0；第3辆共载重为9.5 t，行驶38 km，路径为0-15-12-13-11-17-18-0（简记①：0-2-3-4-5-20-7-6-0；0-16-9-19-14-8-10-1-0；0-15-12-13-11-17-18-0），如图2所示。

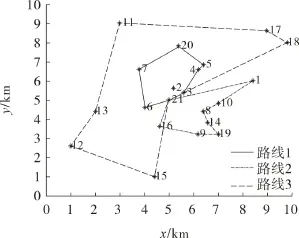
图2　初始车辆行驶路径方案Fig.2 Initial Vehicle Routing Scheme

对第一个车辆行驶路径方案进行邻域搜索，再产生9个初始方案，方法如下：

（a）同一车辆，将某2个待救点位置进行互换，共3种方案。

每辆车历经的第2，4点交换；每辆车历经的第3，5点交换；每辆车历经的第4，7点交换。

（b）两个车辆路线，各选取一个待救点位置进行互换，共3种方案。

第1，2辆车所历经的第3点交换；第1，3辆车所历经的4点交换；第2，3辆车所历经的6点交换。

（c）两个车辆路线，取前者当中某个待救点，将其插入到后者车辆路径当中，共3种方案。

将第1辆车经过的第2待救点，转移到第2辆车经过的第2待救点；将第1辆车经过的第2待救点，转移到第3辆车经过的第2待救点；将第2辆车经过的第5待救点，转移到第3辆车经过的第5待救点。

3）全局寻优

将以上10个应急物资配送车辆路径方案及对应的目标函数值（由式（5），（6）计算得出）看作萤火虫初始种群，根据惯性权重萤火虫算法进行求解得最优的10个路径方案及时间值。以①车辆行驶路径方案为例，再次进行邻域搜索，比较当前萤火虫亮度值和候选萤火虫亮度值，再根据位置更新公式实现萤火虫位置的优化，经过200次迭代，最终得出①方案对应的最优结果，记作①"，同样方法，得到另外9个最优方案。全局搜索环境下车辆耗时的寻优结果如图3所示。

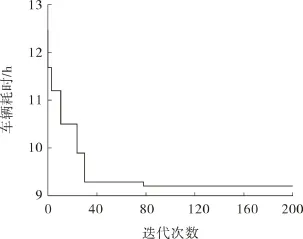
图3　全局搜索寻优结果Fig.3 Global Search Optimization Results

4）混沌序列

从上述10个最优方案当中选取目标值最小的前2个方案。路径方案A（0-2-14-6-5-4-17-18-1-0；0-3-10-19-13-7-11-0；0-8-9-16-15-12-20-0），车辆总行驶时间为9.312 h，车辆总行驶距离为76.4 km，车辆总行驶所耗成本382元；路径方案B（0-2-14-6-4-5-17-18-1-0；0-3-10-19-13-7-11-0；0-8-9-16-15-12-20-0），车辆总行驶时间为9.191 h，车辆总行驶距离为75.6 km，车辆总行驶所耗成本378元。

将以上两个结果对应的萤火虫位置信息，按照式（17）映射到0到1之间的混沌参量，其中解为1维空间（j=1），xmin代表路径方案A（0-2-14-6-5-4-17-18-1-0；0-3-10-19-13-7-11-0；0-8-9-16-15-12-20-0）作为搜索空间下限，xmax代表路径方案B（0-2-14-6-4-5-17-18-1-0；0-3-10-19-13-7-11-0；0-89-16-15-12-20-0）作为搜索空间上限。

5）局部寻优

在局部寻优过程中先不考虑救援中心，把路径方案看作20进制的一个数字（且每个位置上的数字不重复），由此可根据式（17）来实现方案A和方案B的［0，1］映射。需要注意的是，在搜索的过程中，会产生不可行解，对于不可行解点进行“+1”处理，直至找到该数值的最近可行解，然后通过式（18）进行循环比较择优，在限制的迭代次数内得到最优局部解点。局部搜索环境下车辆耗时的寻优结果如图4所示。

图4　局部搜索寻优结果Fig.4 Local Search Optimization Curve

3.3结果

通过先后对解集进行全局搜索及局部寻优，最后得到以车辆行驶时间最短为目标的前三组最优解，如表2所示。

表2　路径寻优方案Tab.2 Route Optimization Scheme

从上表可以看出车辆行驶路径方案耗时最少为9.067 h，则救援时间可接受范围是［9.067，9.248］（由［Tmin,Tmin（1%+2%）］计算得出）。以上3个方案的车辆行驶时间值均在可接受范围以内，则选取其中所耗成本最低的方案作为最优方案，即方案2：共派出3辆救援车进行应急物资配送，总路线长度为72.8 km，共耗时9.153 h，车辆行驶所耗成本为364元。3辆救援车的具体路径分别为：0-14-6-2-4-5-17-18-1-0；0-3-10-19-13-11-7-0；0-8-9-16-15-12-20-0，如图5所示。

为进一步证明提出的两阶段式混沌萤火虫算法在求解过程与求解结果中的优越性，文中禁忌搜索算法对相同的案例进行求解，2种算法求解结果对比见表3。由表3可看出，本文给出的混沌萤火虫算法寻优能力强、车辆行驶耗时更短，费用更少。

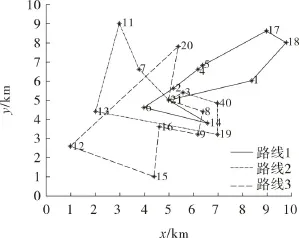
图5　车辆行驶路径最优方案Fig.5 Vehicle Travel Path Optimal Plan

表3　两种算法结果对比Tab.3 Comparison Of TwoAlgorithms

4　结　语

本文主要分析了城市上下班高峰期环境下道路车流量和道路通行容量对应急物资配送车辆行驶速度的影响。在模型求解过程中，通过介入惯性权重和混沌算法有效地平衡了萤火虫算法的全局搜索能力和局部寻优能力。算例结果表明，在求解突发事件情境下应急救援车辆路径优化问题时，新模型及算法相对于就算法的求解结果更优，以耗时和费用为目标函数时，总耗时更少，总费用更少，所提出的路径优化模型及算法对于应急救援工作的顺利开展有一定的指导性意义。

不足之处在于选择车辆路径时假设所有节点之间均可以通行，并且直接取绝对值距离作为节点间距离，而城市实际路网错综复杂、各节点间的道路方向多种多样，因此模拟出城市实际路网作为路径寻优的依据、计算出精准的节点间距离是应急救援车辆路径寻优的下一步研究重点。

［1］陈则辉，刘诚，吕品，等.不确定环境下应急物资配送问题研究［J］.铁道科学与工程学报，2014（5）：82-89.

［2］李创.国内外应急物流研究综述［J］.华东经济管理，2013，27（6）：160-165.

［3］DANTIZIG G，RAMSER J.The truck dispatching pmblem［J］.Management Science，1959，6：80-91.

［4］BALCIKB，BEAMONBM，SMILOWITZK.Lastmiledis-tributioninhumanitarianrelief［J］.JournalofIntelligentTransportation System，2008，12（2）：51-63.

［5］ARAZ C，SELIM H，OZKARAHAN I.A fuzzy multi-objective covering-based vehicle location model for emergency services［J］. Computers&Operations Research，2007，34（3）：705-726.

［6］PRETOLANI D.A directed hypergraph model for random time-dependent shortest path［J］.European Journal of Operational Research，2000，123（8）：315-342.

［7］马祖军，代颖，李双琳.带限制期的震后应急物资配送模糊多目标开放式定位-路径问题［J］.系统管理学报，2014，23（5）：658-667.

［8］代颖，马祖军.应急物流系统中的随机定位-路径问题［J］.系统管理学报，2012，21（2）：212-217.

［9］乔茹，章小兵，赵光兴.基于改进蚁群算法的移动机器人全局路径规划［J］.安徽工业大学学报（自然科学版），2009，26（1）：77-80.

［10］姜金贵，张鹏飞.基于改进蚁群算法的城市内涝救援路径优化［J］.计算机应用，2014，34（7）：2103-2106.

［11］PUREZA V M，FRANCA P M.Vehicle routing problems via tabu search metaheuritic［R］.Centre De Recherche Sur Les Transports Publication，1991.

［12］TORKIA，SOMHON S，ENKAWAT.Acompetitive neural network algorithm for solving vehicle routing problem［J］.Computers &Industrial Engineering，1997，33（3）：473-476.

［13］宋晓宇，刘锋，常春光.面向应急物资调度的一种灰色规划模型［J］.计算机应用研究，2010，27（4）：1259-1262.

［14］管小俊，王喜富，王翠华，等.基于竞争的物流中心选址双层规划模型及算法研究［J］.武汉理工大学学报（交通科学与工程版），2009，33（5）：956-959.

［15］陈荣，李超群.基于ABC法和自适应混合遗传算法的仓储区域布局优化策略［J］.安徽工业大学学报（自然科学版），2011，28（2）：183-187.

［16］刘长平，叶春明.具有混沌搜索策略的萤火虫优化算法［J］.系统管理学报，2013，22（4）：538-543.

［17］汤金春，王培珍.基于遗传算法的钢锭配切优化［J］.安徽工业大学学报（自然科学版），2012，29（1）：67-69.

［18］郜振华，梅莉，祝远鉴.复合策略惯性权重的粒子群优化算法［J］.计算机应用，2012，32（8）：2216-2218.

责任编辑：丁吉海

Route Optimization of Emergency Material Distribution under Urban Emergency Situations

WANG Fuyu1，2，YE Chunming2，WANG Tao1
（1.School of management science and Engineering，Anhui University of Technology，Ma'anshan 243032，China；2.School of management，University of Shanghai for Science and Technology，Shanghai 200093，China）

Aiming at the take of the vehicle routing optimization of emergency material distribution in the urban emergency environment，the influence of urban road congestion on the speed of the vehicle was analyzed.Take the least time and cost of the vehicle as object，a routing optimization model of bi-level programming is built.To improve the global search and local search capability，an improved two stage firefly algorithm was employed to solve the problem.The numerical example shows that the proposed model and algorithm can effectively solve the problem of emergency material distribution in urban emergency.

emergency rescue；route optimization；two-level theory；firefly algorithm

TP391

Adoi：10.3969/j.issn.1671-7872.2016.02.016

1671-7872（2016）02-0177-08

2015-11-13

国家自然科学基金项目（71271138）；教育部人文社会科学青年基金项目（14YJC630119）；住建部软科学研究项目（2015-R2-057）；安徽省高校人文社科研究重大项目（SK2014ZD016）

王付宇（1977-），男，河南泌阳人，副教授，主要研究方向为智能优化、工业工程。