关于拟-σ-空间及拟-Gδ-对角线的注记

吴代龙（马鞍山师范高等专科学校，安徽马鞍山243041）

关于拟-σ-空间及拟-Gδ-对角线的注记

吴代龙
（马鞍山师范高等专科学校，安徽马鞍山243041）

通过对拟-σ-空间及拟-Gδ-对角线性质的研究，得到广义序拓扑空间可度量化的条件及具有拟-Gδ-对角线的线性序空间的结果，改善了文献［2］中关于拟-σ-空间及拟-Gδ-对角线的部分结果，主要结论为：X为 σ-空间当且仅当X为拟-σ-空间；具有拟-Gδ-对角线的线性序空间为Θ-空间。

g-函数；拟-σ-空间；拟-Gδ-对角线

作为对度量空间的推广，σ-空间是一类重要的广义度量空间，文献［1］给出了关于σ-空间的刻画及其与其它空间类的关系等重要结果。Mohamad在文献［2］中引入拟-σ-空间的概念来推广σ-空间，证明了第一可数的广义序空间X可度量化当且仅当X为拟-σ-空间。Gδ-对角线这一概念在拓扑空间的度量化问题中起着重要的作用，如：具有Gδ-对角线的可数紧空间为紧度量空间［1］。作为对Gδ-对角线概念的推广，Hodel在文献［3］中引入拟-Gδ-对角线的概念，之后的研究表明拟-Gδ-对角线这一概念在讨论拓扑空间类之间的关系时同样起着重要的作用，如：具有拟-Gδ-对角线的正则θ加细，β空间为半层空间［3］。Mohamad在文献［2］中讨论了具有拟-Gδ-对角线的线性序空间的性质，证明了具有拟-Gδ-对角线的线性序空间为θ-空间及具有拟对角线的线性序空间为空间。近年来，具有拟-Gδ-对角线的空间的性质及其与其它空间的关系得到了广泛的关注。如Jiang［4］研究具有σ-离散闭稠密子集的广义序空间的性质，证明在具有σ-离散闭稠密子集的广义序空间X中，拟-Gδ-对角线，拟对角线，Gδ-对角线，G*δ-对角线等性质均等价于X为CSS空间；Lin［5］研究拓扑群中拟-Gδ-对角线的性质，证明若非局部紧拓扑群G关于bG的剩余具有拟-Gδ-对角线，则G与bG均为可分度量空间。本文在此基础上探讨拟-σ-空间及拟-Gδ-对角线的问题。

1　定　义

定义1［6］设G为空间X的子集族，若对每一x∈X，存在x的开邻域U使得U至多与G的一个（有限多个）元相交，则称G为离散（局部有限）集族；若对每一x∈X，G中至多有有限多个元含x，则称G为点有限集族。

定义4［9］若映射g：N×X→T满足：对每一x∈X及n∈N，x∈g（n+1,x）⊂g（n,x），则称g为X上的g-函数。

文献［9-10］中给出下列条件：

（γ）若对每一n∈N，yn∈g（n,x）且xn∈g（n,yn），则x为的聚点；

（Θ）若对每一n∈N，｛x,xn｝⊂g（n,yn）且yn有聚点，则x为的聚点；

（θ）若对每一n∈N，｛x,xn｝⊂g（n,yn）且yn∈g（n,x），则x为的聚点。

若存在空间X上的g-函数g满足条件（γ），则称X为γ-空间，相应的g-函数称为γ-函数，其余定义类似。

2　拟-σ-空间

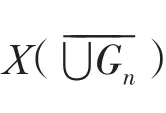
局部有限情形可类似证明。

由引理1立即可得下述定理。

定理1 X为σ-空间当且仅当X为拟-σ-空间。

由于正则σ-空间为半层空间，而半层的广义序空间可度量化，故由定理1可得下述推论。

推论1广义序空间X可度量化当且仅当X为拟-σ-空间。

推论1改进了文献［2］中的下述两个结果。

定理2［2］设X为第一可数的广义序空间，则X可度量化当且仅当X为拟-σ-空间。

定理3［2］广义序空间X可度量化当且仅当X为具有拟-Gδ-对角线的拟-σ-空间。

3　拟-Gδ-对角线

Mohamad在文献［2］中证明了具有拟-Gδ-对角线的线性序空间为θ-空间，本文得出下述更强的结果。

定理4对线性序空间X，下列等价：

1）X具有拟-Gδ-对角线；

2）X为拟可展空间；

3）X具有σ-点有限基。

设x∈X，U为x的开邻域。往证存在k,l∈N使得x∈st（x,Akl）⊂U，仅对x不是X的端点的情形给出证明，对x是X的端点的情形可类似证明。设x不是X的端点，则存在开区间使得由于为X的拟-Gδ-对角线，存在k,l∈N使得x∈st（x,Gk）⊂X｛a｝且x∈st（x,Gl）⊂X｛b｝，则st（x,Akl）为X的含点x的凸集但不含点a和点b，故，这表明｛Amn：m,n∈N｝为X的拟展开列。

（2）⇔（3）见文献［8］。（2）⇒（1）显然。且蕴含关系：

X具有σ-点有限基⇒X为γ-空间⇒X为Θ-空间⇒X为θ-空间

由定理4及上述关系可得：

推论2具有拟-Gδ-对角线的线性序空间为Θ-空间。

推论2改善了文献［2］中的下述结果：

定理5［2］具有拟-Gδ-对角线的线性序空间为θ-空间

定理6［2］具有拟对角线的线性序空间为Θ-空间。

4　结　论

通过证明拟-σ-空间等价于σ-空间，得出拟-σ广义序拓扑空间可度量化这一结论，从而改善了文献［2］中的两个结果：1）第一可数的拟-σ广义序拓扑空间可度量化；2）具有拟-Gδ-对角线的拟-σ广义序拓扑空间可度量化。

此外，证明了具有拟-Gδ-对角线的线性序空间为Θ-空间，由于Θ-空间为θ-空间，拟对角线为拟-Gδ-对角线，故这一结论改善了文献［2］中的另外两个结果：1）具有拟-Gδ-对角线的线性序空间为θ-空间；2）具有拟对角线的线性序空间为Θ-空间。

［1］林寿.广义度量空间与映射［M］.2版.北京：科学出版社，2007.

［2］MOHAMADAM.Some results on quasi-σandθ-spaces［J］.Houston Journal of Mathematics，2001，27（1）：59-65.

［3］HODEL R E.Metrizability of topological spaces［J］.Pacific Journal of Mathematics，1974，55（2）：441-459.

［4］JIANG G H.Some results on CSS and quarter-stratifiable GO-spaces［J］.Topology Proceedings，2013，42：221-236.

［5］LIN F C.Local properties on the remainders of the topological groups［J］.Kodai Mathematical Journal，2011，34：505-518.

［6］ENGELKING R.General Topology［M］.Warszawa：Polish Scientific Publishers，1977.

［7］MOHAMAD A M.Conditions which imply metrizability in some generalized metric spaces［J］.Topology Proceedings，1999，24：215-232.

［8］BENNETT H R.A note on point-countability in linearly ordered spaces［J］.Proceedings of the American Mathematical Society，1971，28（2）：598-606.

［9］HODEL R E.Spaces defined by sequence of open covers which guarantee that certain sequences have cluster points［J］.Duke Mathematical Journal，1972，39（2）：253-263.

［10］FLETCHER P，LINDGREN W F.OnwΔ-spaces，wσ-spaces andΣ#-spaces［J］.Pacific Journal of Mathematics，1977，71（2）：419-428.

［11］HEATH R W，HODEL R E.Characterizations ofσ-spaces［J］.Fund Math，1973，77（3）：271-275.

［12］MARTIN H W.Metrizability of M-spaces［J］.Canadian Journal of Mathematics，1973，25（4）：840-841.

［13］MARTIN II H W.Metrization and Submetrization of Topological Spaces［D］.Pittsburgh：University of Pittsburgh，1973.

［14］CREEDE G D.Concerning semi-stratifiable spaces［J］.Pacific Journal of Mathematics，1970，32（1）：47-54.

责任编辑：丁吉海

Remarks on Quasi-σ-Spaces and Quasi-Gδ-Diagonals

WU Dailong
（Ma'anshan Teacher'College，Ma'anshan 243041，China）

By studying the properties of quasi-σ-spaces and quasi-Gδ-diagonals，some conditions on the metrizability of generalized ordered topological spaces and some results around linearly ordered topological spaces，which have quasi-Gδ-diagonals are obtained.These results modify some related results concerning quasiσ-spaces and quasi-Gδ-diagonals in the literature.The main results are：X is aσ-space if and only if it is a quasi-σspace；Alinearly ordered topological space with a quasi-Gδ-diagonal is aΘ-space.

g-functions；quasi-σ-spaces；quasi-Gδ-diagonals

O189.1

Adoi：10.3969/j.issn/1671-7872.2016.02.017

1671-7872（2016）02-0185-04

2015-12-01

校级自然科学基金项目（2016xjkyxm18）

吴代龙（1980-），男，安徽怀宁人，硕士，助教，主要研究方向为一般拓扑学。