一种基于量子密钥与混沌映射的图像加密新方法

张　克，高会新（.东北大学计算机科学与工程学院，沈阳089；.济钢集团国际工程技术有限公司，济南500）

一种基于量子密钥与混沌映射的图像加密新方法

张克1，高会新2
（1.东北大学计算机科学与工程学院，沈阳110819；2.济钢集团国际工程技术有限公司，济南250101）

依据量子密钥分配协议具有可证明的安全性及混沌序列的伪随机性，提出一种基于量子密钥与混沌映射相结合的图像加密新方法。根据BB84协议获得初始量子密钥，采用数据协商方式对初始密钥进行纠错，再将所得量子密钥与Logistic混沌序列相融合，生成最终的密钥流，以此对图像像素值通过异或运算进行置换实现图像加密。仿真结果与分析表明：本文方法在保证密钥传输安全性的同时，可以更为有效地掩盖图像的统计信息、抵御明文攻击；密钥流对于初始参数具有高敏感性。

量子密钥；BB84协议；密钥分配；混沌映射；图像加密

传统的加密方法中密文的安全性主要依赖于密钥的隐密性和算法的复杂程度。由Major等提出的“一次一密乱码本”（one time pad）的加密系统虽信息论中证明其具有绝对的安全性［1］，但实际应用中，由于合法的通信双方在获取共享密钥过程中进行的通信安全性难以得到保证，使得这一体系难以广泛应用。Shor［2］设计的大数质因子分解的量子算法使求解大数质因子从NP难解问题成为可解的P问题，预示着一旦量子计算机得以实现，现有的公钥体系将不再安全。因此，寻找更加安全的密钥分配算法再次成为研究热点。量子态的特性从物理机理上给出了一种解决密钥分配问题的新思路。基于量子理论的BB84协议是迄今被证明为无条件安全的协议之一［3］，具有可证明的安全性并在密钥分配过程中可实现对外界干扰的检测机制。Wakes等［4］设计了一种将量子密钥分配融于经典Vernam算法的密码系统，并对256色的位图进行加密；王培珍等［5］采用扩展的六态方案对图像进行加密，获得了良好的效果。但这些方法难以掩盖图像的统计特性。

混沌系统是一种具有复杂伪随机性的非线性系统，具有不可预测、非周期、伪随机及对初始值敏感等特点，符合混淆原则，可直接用于一次一密的加密算法，因此成为构造密码系统的理想选择［6-7］。近年来，已有研究将混沌系统用于图像加密，并取得了一定的效果［8-10］，但该类方法易受到相空间重构方法的攻击［11］。鉴于此，本文将BB84协议与混沌映射相结合，提出一种改进的图像加密算法。由于混沌序列的伪随机性，算法在满足密钥安全性的基础上可更好地隐藏原图像的统计信息。

1　密钥的生成

1.1基于BB84协议的量子密钥

BB84协议是1984年由Bennett和Brassard提出的第一个量子密钥分配协议［12］。协议采用单光子的偏振态进行编码。偏振态由二维希尔伯特空间的两组正交基（线性基和旋转基）表示，线性基以“+”表示，对应于线偏振态；旋转基以“×”表示，对应于圆偏振态。每个基中有相互正交的两个态，线性基：旋转基：偏振态满足：

设Alice为发送方，Bob为接收方。协议描述如下。

1）Alice随机选择一组测量基“+”或“×”制备单光子偏振态，Alice传输的单光子偏振态将会随机地表现为|↑＞,|→＞或|↗＞,|↖＞。

2）Alice通过量子传输信道将其制备的量子偏振态发送给Bob，量子比特间等时间间隔。

3）Bob选定一组随机测量基序列检测其接收到的光子偏振态。

4）Bob通过经典信道通知Alice其选用的测量基序列。

5）Alice告知Bob采用的测量基中正确的部分，双方保存相同测量基对应的检测结果。

6）根据相同测量基所得测量结果的出错率判定是否存在攻击。选定阈值ε，当出错率≤ε时，继续执行下面的操作，否则终止。

7）通信双方按照如下方式对量子态进行二进制（比特位）编码：|→＞=＞0,|↑＞=＞1,|↗＞=＞0,|↖＞=＞1，得初始密钥。

8）采用数据协商方式对初始密钥纠错。通信双方公开选取初始密钥中1个随机比特位子集，比较该子集中比特的校验位。若双方所选子集的校验位相同，放弃该比特。对k个独立的子集重复进行校验位的比较，确保通信双方共享密钥相同的概率为1-2k。

实际传输过程中，因光子丢失或探测器灵敏度等问题会导致Bob接收到的光子数比Alice发送的要少。假设Alice向Bob传送了10个比特的信息，量子密钥产生的过程如图1。图中：①Alice使用的测量基序列；②Alice发送的量子比特串；③Bob使用的测量基序列；④Bob的测量结果；⑤通信双方保存的相同的测量结果；⑥所得初始量子比特流；⑦双方密商；⑧最终密钥流；空格表示未检测到偏振态。

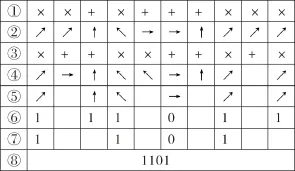
图1　BB84协议量子密钥产生过程Fig.1 Process of quantum key with BB84 protocol

1.2Logistic混沌映射

混沌运动具有以下特征：既非周期又不收敛，运动轨迹上的点遍历整个区域；运动轨迹在有限区域内不断伸缩、折叠，使系统输出类似随机噪声；系统运动对初始值和控制参数极为敏感。这些特征决定了混沌映射用于图像加密技术优越性。文中混沌序列采用Logistic映射产生，如式（2）。

其中：3.569 946≤μ≤4；f0∈（0,1），为序列的初始值。

1.3最终密钥流

将1.1中由量子协议生成的密钥与1.2中Logistic映射产生的混沌序列进行异或运算，生成最终用于图像加密的密钥流。

2　图像加密算法

直接运用量子密钥对图像加密难以掩盖原图像统计信息。为有效掩盖明文的统计特性，在加密算法上采用量子密钥与混沌系统相结合的方法。对于M×N的灰度图像，加密算法描述如下：

1）Alice产生随机二进制序列和随机测量基序列，测量基由变量A表示，变量的取值为t或t1；产生对应的偏振态序列B，t或 t1分别表示测量基对应的4个偏振状态，取值为p，p′和p1，pt′。其中t对应偏振态p，p′，t1对应对应偏振态p1，pt′；

2）Alice向Bob发送偏振态序列B；

3）Bob随机产生测量基序列，测量收到的序列；

4）通信双方比较测量基，保留由相同测量基检测所得结果，计算测量结果的出错率ε，当大于设定的阈值时，返回步骤1）；

5）对保留的量子态进行编码，编码规则如表1；

6）对结果用奇偶校验法进行再协商，获得最终量子密钥串Q；

7）由式（2）获得混沌序列 fk（k=M×N），取 fk′= 1 000）mod 256；

8）当Q的长度小于M×N时，循环使用序列Q，并从中取Q′，使Q′的长度等于M×N。将 fk'与Q′异或运算，得最终密钥C；

9）将图像数据与密钥序列C作异或运算，得加密后图像。

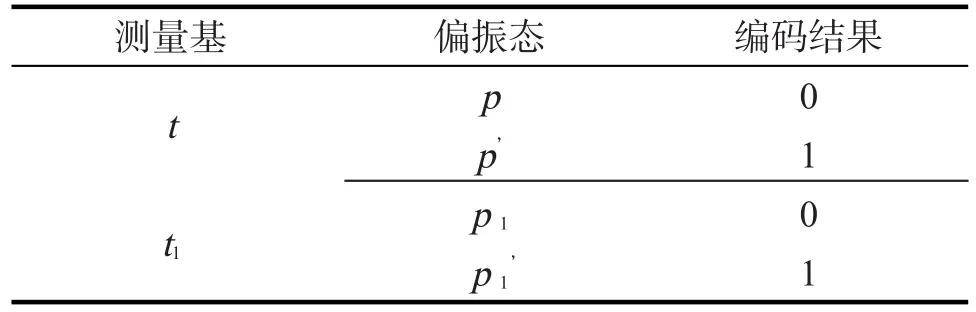
表1　编码规则Tab.1 Encoding rules

3　算法的仿真结果及分析

3.1算法仿真结果

算法在经典计算机上采用VC2005编程实现。发送的随机二进制序列的位数为100 000；图像大小为256×256；Logistic混沌系统的初始值取 f0=0.2，μ=3.9；ε=0.05。图2为对Lena图像加密的仿真结果，其中：图2（a）为原始图像；图2（b）为采用单一量子密钥（BB84）加密结果；图2（c）是本文方法加密结果。从结果不难看出，采用本文量子密钥与混沌系统相结合的方法产生的密文图像，其像素值在空间域的分布更加均匀。

图2　图像加密前后对比Fig.2 Comparison between original image and encrypted ones

3.2统计分析

统计攻击是一种常见的攻击方式，文中通过对加密前后图像直方图的对比和相邻像素的相关性来分析算法的安全性。

1）直方图分析。直方图能反映图像的像素值分布规律。图3是对应于图2的直方图。比较图3（a），（b）与（c）可看出，加密前后的直方图发生了明显的变化：加密后的直方图分布较为均匀；较之图3（b），图3（c）的分布更为均匀，表明本文方法能更好地掩盖原图像的像素值分布规律，从而可以更为有效地抵抗统计攻击。

图3　加密前后图像直方图Fig.3 Histograms of original image and encrypted ones

2）相邻像素相关性分析。图像中相邻像素间具有强相关性。为了抵抗统计攻击，需降低相邻像素间的相关性。采用文献［13］的方法计算加密前后水平和垂直方向像素间相关性，结果如图4。

图4　图像加密前后像素相关性Fig.4 Correlation between pixels of original and encrypted images

由图4（a），（d）可看出，原图像水平与垂直相邻像素的相关性，集中分布于对角线左右，表明其相邻像素间相关性大。由图4（b），（c），（e），（f）可看出，采用2种方法加密后图像的水平与垂直相邻像素的相关性呈随机分布状态，表明其相邻像素间相关性小。为进一步讨论加密前后相邻像素间相关性，采用相关系数Cr分析［14］。

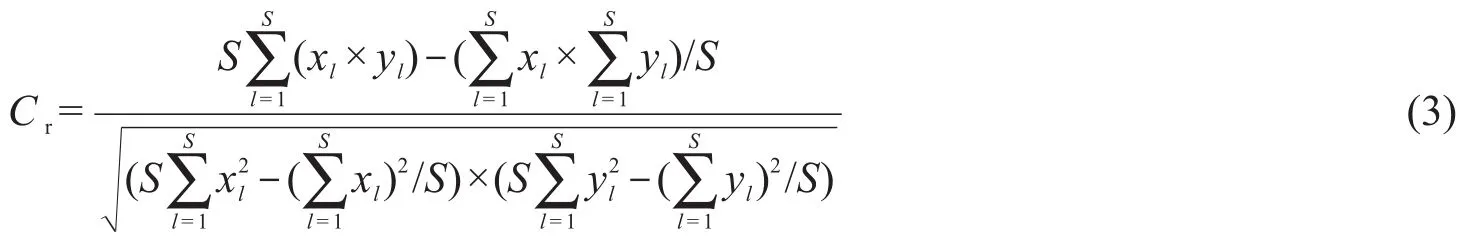
式中：x和y是相邻的像素值；S是像素总数。相关系数计算结果见表2。由表2可以看出：加密前相关系数接近于1，表明图像中像素间具有强相关性；加密后相关系数减小，表明这种相关性被破坏；采用本文方法加密后所得图像相关系数比单一量子密钥加密图像相关系数更小（约一个数量级），表明本文方法可以更为有效地掩盖图像的统计特性、抵御明文攻击。

表2　像素相关性计算结果Tab.2 Correlation coefficients for two adjacent pixels

3.3密钥敏感性分析

为了测试密钥对于参数初始值的敏感性，引入密文变化率（Number of pixels change rate，NPCR）［14］。取两组不同初始值 f0和 μ，将Logistic初始参数作微小偏移，用生成密钥分别对图1（a）加密，得加密后图像C1，C2，其（i,j）处像素灰度值分别用C1（i,j）和C2（i,j）表示。如果C1（i,j）=C2（i,j），则 D（i,j）=0，否则D（i,j）=1。密文变化率rNPCR定义如下

不难看出，rNPCR值越大，不同密钥加密所得密文图像变化越大。取 f0=0.2，μ=3.9，并分别取Δf0=0.000 000 01或Δμ=0.000 000 01，结果如表3。

表3　初始参量对密文变化率的影响Tab.3 Effect of initial parameters on rNPCR

由表3可以看出，虽然生成密钥的初始参数差别微小，但是由此加密之后所得密文图像的rNPCR相差很大（＞99%），表明本文方法所生成密钥对初始参数的敏感性很强。

4　结　论

借助量子密钥分配具有可证明的安全性及混沌序列具有良好的伪随机性，提出了一种基于量子密钥与混沌映射相结合的图像加密新方法。仿真结果与分析表明：本文加密算法有效降低了密文图像相邻像素间的相关性，且使密文分布更为均匀，增强了对明文图像统计特性及明文攻击的抵御能力；混沌映射对于初始参数极其敏感，从而使密钥的安全性进一步提高。

［1］SHANNON C E.Communication theory of secure system［J］.Bell System Technical Journal，1949，28（4）：656-715.

［2］SHOR P W.Polynomial-time algorithms for prime factorization and discrete logarithms on a quantum computer［J］.SIAM Journal on Computing，1997，26（5）：1484-1509.

［3］LO H K，CHAU H F.Unconditional security of quantum key distribution over arbitrarily long distances［J］.Science，2001，283：2050-2057.

［4］WAKES E I K，SANTORI C.Quantum cryptography with a photon turnstile［J］.Nature，2002，420：762-76.

［5］王培珍，王友兰，程木田.一种基于六态量子密钥的图像加密算法［J］.安徽工业大学学报（自然科学版），2014，31（3）：303-308.

［6］贾红艳，陈增强，袁著祉.一个大范围超混沌系统的生成和电路实现［J］.物理学报，2009，58（7）：4469-4476.

［7］PAREEK N K，PATIDAR V，SUD K K.Discrete chaotic cryptograph using external key［J］.Physics Letters A，2003，309（1/2）：75-82.

［8］WANG P Z，GAO H X，CHENG M T，et al.A new image encryption algorithm based on hyperchaotic mapping［C］//Proceedings of the IEEE International Conference on Computer，Application&System Modeling.Taiyuan，2010：428-432.

［9］许冰，孙永维，李洋，等.基于高维混沌系统的图像加密改进算法［J］.吉林大学学报（信息科学版），2012，30（1）：3-17.

［10］徐刚，张亚东，张新祥，等.基于交替迭代混沌系统的图像加密算法［J］.北京科技大学学报，2012，34（4）：464-470.

［11］文昌辞，王沁，苗晓宁，等.数字图像加密综述［J］.计算机科学学报，2012，39（12）：6-10.

［12］BENNETT C H，BRASSARD G.Quantum cryptography：public-key distribution and coin tossing［C］//Proceedings of the IEEE International Conference on Computers，Systems，and Signal Processing.Bangalore，India，1984：175-179.

［13］PAREEK N K，VINOD P，SUD K K.A symmetric image encryption scheme based on 3D chaotic cat maps［J］.Chaos Solutions and Fractals，2004，21：749-761.

［14］CHEN G R，MAO Y B，CHARLES K C.Image encryption using chaotic logistic map［J］.Image and Vision Computing，2006，24：926-934.

责任编辑：何莉

ANew Image EncryptionAlgorithm Based on Quantum Key and Chaotic Mapping

ZHANG Ke1，GAO Huixin2
（1.School of Computer Science&Engineering，Northeastern University，Shenyang 110819；2.Jigang International Engineering&Technology Co.Ltd.，Jinan 250101，China）

According to the certifiable security of quantum key distribution protocol and pseudo random characteristics of the chaotic sequence，a new image encryption method that combined quantum key and chaotic mapping was proposed.Firstly，initial quantum key was obtained with BB84 protocol，then quantum key was formed after error checking for the initial key with data consulting approach，and the last key stream was achieved by combining the quantum key and chaotic sequence from Logistic mapping.Lastly，pixel values were replaced with XOR operation of pixel values and the last key stream，and image was encrypted.Simulation results and analysis show that，the new cryptographic algorithm can more effectively resist statistics-based and plain text attack，while ensuring the security of key transformation；the key stream results from the new method is highly sensitive to initial parameters.

quantum key；BB84 protocol；key distribution；chaotic mapping；image encryption

TP309.2

Adoi：10.3969/j.issn.1671-7872.2016.02.014

1671-7872（2016）02-0167-05

2015-09-20

张克（1993-），男，安徽怀宁人，硕士生，主要研究方向为信息处理。