中职计算机专业算法学习七要素

刘光　裴鹏飞

（宣城市信息工程学校　宣城　242000）

中职计算机专业算法学习七要素

刘光裴鹏飞

（宣城市信息工程学校宣城242000）

中职计算机应用专业学生，学习编程语言的难点是算法基础差。因此如何提高中职计算机应用专业的学生在校期间的算法学习，就是重中之重了。本文浅谈了中职学生学习算法的方法、思路以及注意事项。

算法步骤编程

程序是用来在计算机上实现现实世界中的业务和娱乐活动的。为了达到这个目的，程序员们需要结合计算机的特性，用程序来表示现实世界中对问题的处理步骤，即处理流程。在绝大多数情况下，为了达到某个目的需要进行若干步处理。例如为了达到“计算出两个数相加的结果”这个目的，就需要依次完成以下三个步骤，即“输入数值”“执行加法运算”“展示结果”。像这样的处理步骤，就被称为算法。

在算法中，有表示程序整体大流程的算法，也有表示程序局部小流程的算法。

一、算法是程序设计的“熟语”

学习编程语言与学习外语很像。为了将自己的想法完整地传达给对方，仅仅死记硬背单词和语法是不够的，只有学会了对话中常用的熟语，才能流利地对话。学习C语言、Java和BASIC等编程语言也是如此。仅仅囫囵吞枣地把关键词和语法记下来，是无法流利地和计算机对话的，可是一旦了解了算法就能将自己的想法完整地传达给计算机了。因为算法就相当于是程序设计中的熟语。

“令人生畏且难以掌握”“和自己无缘”，这是中职计算机专业学生对算法留下的印象。诚然，有那种无法轻松理解、难以掌握的算法，但是并不是说只有把那种由智慧超群的学者才能想出的算法全部牢记心中才能编写程序，简单的算法也是有的。而且学生自己也不妨去思考一些原创的算法。只要理清在现实世界解决问题的步骤，再结合计算机的特性，就一定能想出算法。思考算法也可以是一件非常有趣的事。下面，笔者将介绍中职计算机专业学生学习、思考算法时的要点。

二、要点1：算法中解决问题的步骤是明确且有限的

百度中关于“算法”的定义是这样描述的：算法（Algorithm）是指解题方案的准确而完整的描述，是一系列解决问题的清晰指令，算法代表着用系统的方法描述解决问题的策略机制。也就是说，能够对一定规范的输入，在有限时间内获得所要求的输出。如果一个算法有缺陷，或不适合于某个问题，执行这个算法将不会解决这个问题。不同的算法可能用不同的时间、空间或效率来完成同样的任务。一个算法的优劣可以用空间复杂度与时间复杂度来衡量。这个定义虽然看起来晦涩，但是正确地解释了什么是算法。

如果用通俗易懂的语言来说，算法就是“把解决问题的步骤无一遗漏地用文字或图表示出来”。要是把这里的“用文字或图表示”替换为“用编程语言表达”，算法就变成了程序。而且请学生注意这样一个条件，那就是“步骤必须是明确的并且步骤数必须是有限的”。

接下来先举一个具体的例子，请同学们想一想解决“求出12和42的最大公约数”这个问题的算法。最大公约数是指两个整数的公共约数（能整除被除数的数）中最大的数。最大公约数的求解方法应该在小学的数学课上学过了。把两个数写在一排，不断地寻找能够同时整除这两个整数的除数。最后把这些除数相乘就得到了最大公约数（如图1所示）。

用这个方法求出了6是最大公约数，结果正确。但是这些步骤能够称为算法吗？答案是不能，因为步骤不够明确。

步骤1的“用2整除12和42”和步骤2的“用3整除6 和21”，是怎么知道要这样做的呢？寻找能够整除的数字的方法，在这两步中并没有体现。步骤3的“没有能同时整除2和7的除数”，又是怎么知道的呢？而且，到此为止无需后续步骤（即步骤数是有限的）的原因也是不明确的。

其实这些都是凭借人类的“直觉”判断的。在解决问题的步骤中，有了与直觉相关的因素，就不是算法了。既然不是算法，也就不能用程序表示了。

三、要点2：计算机不靠直觉而是机械地解决问题

计算不能自发地思考。因此计算机所执行的由程序表示的算法必须是由机械的步骤所构成。所谓“机械的步骤”，就是不用动任何脑筋，只要按照这个步骤做就一定能完成的意思。众多的学者和前辈程序员们已经发明创造出了很多机械地解决问题的步骤，这些步骤并不依赖人类的直觉。由此所构成的算法被称为“典型算法”。

辗转相除法（又称欧几里得算法）就是一个机械地求解最大公约数问题的算法。在辗转相除法中分为使用除法运算和使用减法运算两种方法。使用减法运算简单易懂，步骤如图2所示。用两个数中较大的数减去较小的数（步骤），反复进行上述步骤，直到两个数的值相等（步骤的终止）。如果最终这两个数相同，那么这个数就是最大公约数。请学生注意以下三点：1.步骤是明确的、完全不依赖直觉的；2.步骤是机械的、不需要动脑筋就能完成的；3.使步骤终止的原因是明确的。

使用辗转相减法求解12和42的最大公约数的程序代码如代码清单-1所示。本文展示的程序都是用VB编程语言编写的（如图3所示）。学生即使读不懂这段程序代码的内容也没有关系，这里需要学生注意的是该算法所描述的步骤是可以直接转换成程序的。

代码清单-1：求解12和42最大公约数的程序

四、要点3：了解并应用典型算法

笔者建议希望从事编程工作的学生手中要有一本能作为算法典籍的书。虽然算法应该由学生自己思考，但是如果遇到了不知道从哪里下手才好的问题，也可以利用这类典籍查查已经发明出来的算法。

作为程序员的修养，表1中列出了笔者认为最低限度应该了解的典型算法。这些算法包括刚刚介绍过的求解最大公约数的“辗转相除法”，判定素数的“埃拉托斯特尼筛法”（将在后面介绍），检索数据的三种算法以及排列数据的两种算法。记住了这些典型算法固然好，但是请学生注意绝不要丢掉自己思考算法的习惯。

表1　主要的典型算法

让学生再试着思考一个具体问题。这次请思考一下解决“求解12和42的最小公倍数”这个问题的算法。所谓最小公倍数就是指两个整数的公共倍数（是一个数几倍的数）中最小的那个数。最小公倍数的求解方法学生在小学的数学课上也应该学过了，但是很可惜求解步骤也是依赖人类的直觉的。请再思考一个适用于计算机的机械的算法。学生说不定会想“反正会有典型算法的吧，比如‘某某氏的某某法’”，然后就纠结于是否还要自己思考。

但是即使查了算法典籍之类的书，也还是找不到求解最小公倍数的算法。为什么呢？因为我们可以通过以下方法求解最小公倍数——用两个整数的乘积除以这两个整数的最大公约数。因此12和42的最小公倍数就是12×42÷ 6=84了。如此简单的算法不能算作典型算法。这个例子说明先自己思考算法，再去应用典型算法这一点很重要。

五、要点4：利用计算机的处理速度

接下来再请学生思考求解“判定91是否是素数”这一问题的算法。在用于判定素数的典型算法中，有一个被称为“埃拉托斯特尼筛法”的算法。在学习这个算法之前，先请学生思考如果是在考试中碰到了这道题，要如何解答呢？

也许有的学生会这样想：用91分别除以比它小的所有正整数，如果没有找到能够整除的数，那么91就是素数。但是，如此繁琐的步骤可行吗？实际上这就是正确答案。埃拉托斯特尼筛法是一种用于把某个范围内的所有素数都筛选出来的算法，比如筛选100以内的所有素数，其基本思路就是用待判定的数除以比它小的所有正整数。例如要判定91是否是素数，只要分别除以2～90之间的每个数就可以了（因为1肯定能够整除任何数，所以从2开始检测）。这个步骤用程序表示的话，就变成了如代码清单-2所示的代码。Mod是用于求除法运算中余数的运算符。如果余数为0则表示可以整除，因此也就知道待判定的数不是素数了。程序执行结果如图4所示。

代码清单-2：判定是否是素数的程序

无论是多么冗长繁琐的步骤，只要明确并且机械就能构成优秀的算法。诸位把算法用程序表示出来让计算机去执行，而计算机会用令人吃惊的速度为我们执行。为了判定91是否是素数，用91除以2～90这89个数的操作一瞬间就可以完成。在思考算法时不防时刻记着，解决问题时是可以利用计算机的处理速度的。

作为利用计算机的处理速度解决问题的另一个例子，请试着求解以下联立方程组。题目是鸡兔同笼问题：鸡和兔子共计10只，把它们的脚加起来共计32只，问鸡和兔子分别有多少只？设有x只鸡，y只兔子，那么就可以列出如下的联立方程组。

六、要点5：：使用编程技巧握升程序执行速度

解决一个问题的算法未必只有一种。在考量用于解决同一个问题的多种算法的优劣时，可以认为转化为程序后，执行时间较短的算法更为优秀。虽然计算机的处理速度快得惊人，但是当处理的数据数值巨大或是数量繁多时还是要花费大量的时间。例如，判定91是否是素数的过程一下子就有结果了，可是要去判定999999937的话'笔者的电脑就要花费大约20分钟之久（言外之意999999937是素数）。

有时稍微往算法中加入一些技巧，就能大幅度地缩短处理时间。在判定素数上，原先的过程是用待判定的数除以比它小的所有正整数，只要在此之上加入一些技巧，改成用待判定的数除以比它的1/2小的所有数，处理时间就会缩短。之所以改成这样是因为没有必要去除以比它的1/2还大的数。通过这一点改进，除法运算的处理时间就能够缩短1/2。

在算法技巧中有个著名的技巧叫作“哨兵”。这个技巧多用在线性搜索（从若干个数据中查找目标数据）等算法中。线性搜索的基本过程是将若干个数据从头到尾，依次逐个比对，直到找到目标数据。

因为鸡和兔子的只数应该都在0～10这个范围内，所以就试着把0～10中的每个数依次代入x和y，只要能够找到使这两个方程同时成立的数值也就求出了答案。利用计算机的处理速度，答案一瞬间就出来了（如代码清单-3和图5所示）。

代码清单-3：求解鸡兔同笼问题的程序

下面还是通过例题来思考吧。假设有100个箱子，里面分别装有一个写有任意数字的纸条，箱子上面标有1～100的序号。现在要从这100个箱子当中查找是否有箱子装有写着要查找数字的纸条。

首先看看不使用哨兵的方法。从第一个箱子开始依次检查每个箱子中的纸条。每检查完一个纸条，还要再检查箱子的编号（用变量N表示），并进一步确认编号是否已超过最后一个编号了。这个过程用流程图表示后如图6所示。

图6所示的过程，虽然看起来似乎没什么问题，但是实际上含有不必要的处理——每回都要检查箱子的编号有没有到100。

为了消除这种不必要的处理，于是添加了一个101号箱子，其中预先放入的纸条上写有正要查找的数字。这种数据就被称为“哨兵”。

通过放入哨兵，就一定能找到要找的数据了。找到要找的数据后，如果该箱子的编号还没有到101就意味着找到了实际的数据；如果该箱子的编号是101，则意味着找到的是哨兵，而没有找到实际的数据。使用了哨兵的流程图如图7所示。需要多次反复检查的就只剩下“第N个箱子中包含要找的数字吗？”这一点了，程序的执行时间也因此大幅度地缩减了。

当笔者第一次得知哨兵的作用时，对其巧妙性感到惊叹，兴奋异常。有些学生会感到“不太明白巧妙在哪里”，那么就讲一个故事来解释哨兵的概念吧。假设某个漆黑的夜晚，学生们在海岸的悬崖边上玩一个游戏（请勿亲身尝试）。诸位站在距悬崖边缘100米的地方，地上每隔1米就任意放1件物品。请找出这些物品中有没有苹果。

学生每前进1米就要捡起地上的物品，检查是否拿到了苹果，同时还要检查有没有到达悬崖的边缘（不检查的话就有可能掉到海里）。也就是说要对这两种检查反复若干次。

使用了哨兵以后，就要先把起点挪到距悬崖边缘101米的地方，再在悬崖的边缘放置一个苹果。这个苹果就是哨兵。通过放置哨兵，学生就一定能找到苹果了。每前进1米时只需检查捡到的物品是不是苹果就可以了。发现是苹果以后，只需站在原地再检查一步开外的情况。如果还没有到达悬崖边缘，就意味着找到了真正要找的苹果。已经达到了悬崖边缘，则说明现在手中的苹果是哨兵，而没有找到真正要找的苹果。

七、要点6：找出数字间的规律

所有的信息都可以用数字表示——这是计算机的特性之一。因此为了构造算法，经常会利用到存在于数字间的规律。例如，请思考一下判定石头剪刀布游戏胜负的算法。如果把石头、剪刀、布分别用数字0、1、2表示，把玩家A做出的手势用变量A表示，玩家B做出的手势用变量B表示，那么变量A和B中所存储的值就是这三个数中的某一个。请以此判断玩家A和B的输赢。

如果算法没有使用任何技巧，也许就会通过枚举表 2中所列出的 3x3=9种组合来判断输赢吧。把这个表格转换成程序后就得到了代码清单-4中的代码。可以看出这是一种冗长而又枯燥的判断方法（代码清单-4和代码清单-5列出的都只是程序的一部分，因此不能直接运行）。

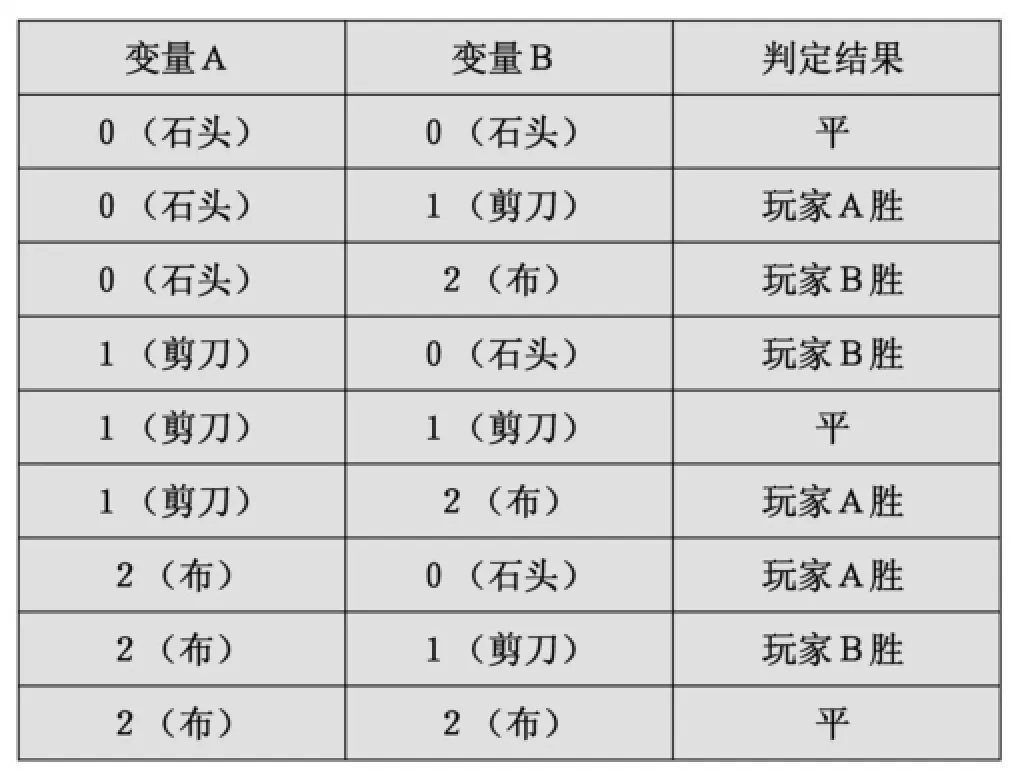
表2　判定石头剪刀布输赢的表

代码清单-4：判断石头剪刀布输赢的程序（方法一）

接下来就试着在此之上稍微加入些技巧吧。请仔细观察表2并找出数字间的一种规律，这个规律可以简单地判定出是玩家A获胜，玩家B获胜，还是平局这三种结果。可能需要习惯一下思维上的转变，但最终应该都可以发现如下的规律：

1、如果变量A和B相等就是“平局”；

2、如果用B+1除以3得到的余数与变量A相等就是“玩家B获胜”；

3、其余的情况都是“玩家A获胜”。

用程序来表示这个规律就得到了如代码清单-5所示的代码。与没有使用任何技巧的代码清单-4中的代码相比，可以发现处理过程简单并且代码短小精焊。当然程序的执行速度也会随之提升。

代码清单-5：判断石头剪刀布输赢的程序（方法二）

构造算法时需要找出数字间的规律不仅适用于数学游戏，编写用于计算工资的应用程序时，计算工资的规则也可以说是一种数字上的规律。如果能够发现“工资=底薪+加班补贴+交通补贴-预扣税款”这样的规律，那么解决问题的步骤就是明确的，步骤数也是有限的，因此构造出的算法也就是优秀的了。

八、要点7：先在纸上考虑算法

最后介绍最为重要的一点，那就是思考算法的时候，要先在纸上用文字或图表描述出解决问题的步骤，而不要立刻开始编写代码。

画流程图就可以方便地把算法用图表示出来，因此请学生大量地、灵活地运用它。如果不想画流程图，也可以用语言把算法描述出来，写成文书。总之先写到纸上这一点很重要。

在纸上画完或写完流程以后，再把具体的数据代入以踉踪流程的处理，确认是否能得到预期的结果。在验算的时候，建议使用简单的数据，这样即使是用心算也能得出正确的结果。例如，要确认辗转相除法的流程，就可以使用数值较小的数做验算，这样就算是用小学所学的求解步骤也能求出最大公约数。如果使用的是数值较大的数，比如123456789和987654321（最大公约数是9），那么就难跟踪流程的处理了。

［1］Donald E.Knuth.计算机程序设计艺术卷1基本算法［M］.人民邮电出版社.2016.1.

［2］王晓华.算法的乐趣［M］.人民邮电出版社.2015.3.

［3］徐士良.数据与算法［M］.清华大学出版社.2014.12.

［4］吴伟昶（韩）.算法设计技巧与分析［M］.电子工业出版社.2010.10.

［5］Frank Nielsen.程序设计与算法［M］.清华大学出版社. 2012.1.

刘 光，男，1968年11月出生，1992年6月本科毕业於安徽师范大学；现任教於宣城市信息工程学校，微机教研组组长，中学一级计算机教师；多次辅导学生参加宣城市技能大赛获一、二等奖，2015年辅导学生参加安徽省技能大赛获计算机检测三等奖。

裴鹏飞，男，1976年2月出生，1998年6月本科毕业於安徽科技学院；现任教於宣城市信息工程学校，教务处主任，中学高级计算机教师；2005年获得宣城市第三届“骨干教师”荣誉称号；2007年获得宣城市第四届“教坛新星”荣誉称号；2011年获得宣城市第四届“学科带头人”荣誉称号；2012年获得安徽省“教坛之星”荣誉称号；2013年获得安徽省“专业带头人”荣誉称号；2016年成立安徽省“裴鹏飞名师工作坊”。）

Seven Elements of Learning to the Algorithm of Computer Specialty in Secondary Vocational Schools

Liu GuangPei Pengfei
（Xuancheng School of Information EngineeringXuancheng242000）

Vocational students majoring in computer applications,the difficulty in learning a programming language is based is poor.Therefore,how to improve vocational students majoring in computer during school learning algorithm,is a top priority.This article talking about vocational students in learning algorithm of methods,ideas and instructions.

AlgorithmStepProgramming

G633.67

A

160615-7311