精密数控车床主轴热误差建模

郭辰光，韩　雪，李　源，谢华龙

(1.辽宁工程技术大学 机械工程学院，辽宁 阜新 123000；2.东北大学 先进制造与自动化技术研究所，辽宁 沈阳 110819)



精密数控车床主轴热误差建模

郭辰光1，2*，韩雪1，李源1，谢华龙2

(1.辽宁工程技术大学 机械工程学院，辽宁 阜新 123000；2.东北大学 先进制造与自动化技术研究所，辽宁 沈阳 110819)

开展了精密数控车床主轴系统热误差补偿的实验与建模方法的研究。建立了精密数控车床主轴系统轴向与径向偏转热误差补偿模型以增强其误差补偿能力，并提高机床加工精度。构建了主轴系统热误差测试平台，应用五点法测试主轴系统热误差，使用热电偶与红外热像仪测量主轴系统温升关键点温度变化数据，应用灰色综合关联分析法实现温度敏感测点辨识。构建了基于粒子滤波重采样粒子群算法的热误差预测模型，对模型预测效果进行评价。结果表明：基于粒子滤波重采样粒子群热误差补偿模型得到的轴向热误差预测残差为-1.29μm～1.55μm，建模精度为95.04%；y向热偏转误差预测残差为-4.68×10-6°～9.66×10-6°，建模精度为91.26%；z向热偏转误差预测残差为-5.83×10-6°～8.59×10-6°，建模精度为93.24%。实验结果证明该热误差补偿模型具有较高的预测精度，具有较强的工程应用价值。

精密数控车床；主轴系统；热误差建模；热误差补偿；粒子滤波重采样粒子群算法

1　引　言

热误差是影响精密机床加工精度的最主要误差源，占精密机床总误差的70%以上[1]。主轴系统是精密机床的核心部件，其结构复杂、散热条件较差，另外由于热源分布不均、零部件材料热膨胀系数不同，导致精密机床主轴系统的温度场复杂多变，主轴系统热误差严重制约着我国精密与超精密加工机床行业的发展。目前，降低主轴系统热误差的方法可归纳为硬件消除法与软件补偿法两种[2-3]。硬件消除法是[4]通过热特性分析，对机床主轴系统结构进行热平衡设计，以辅助冷却系统散热，并采用热膨胀系数较低的材料制备传动部件，以降低主轴系统热误差，但该方法将大大增加机床设计与制造成本。软件补偿法[5]要求建立机床主轴系统温升与热误差之间的映射关系模型，由主轴系统温升数据预测热误差，并通过CNC数控系统对误差进行实时补偿。该方法不需对机床主轴系统结构进行变更设计，具有成本低廉、实施简便、精度稳定性好等特点，因此成为机床热误差补偿研究的重点。

对于软件补偿法而言，精度高、鲁棒性好的补偿模型是实现数控机床热误差补偿的关键。王乾俸[6]等应用回归分析和最小二乘法建立了稳定状态下主轴轴向变形量和时间常数的估计方程，给出了基于指数形式的主轴热误差补偿模型。然而，该模型仅考虑了主轴在不同转速下的轴向变形，未对偏转误差加以量化说明，对工程应用的指导意义有限。杨建国[7]、陈诚[8]等开展了一系列人工神经网络构建机床热误差补偿模型的研究，通过改变神经网络系数、隐含层激励函数、网络拓扑结构、网络模型初值等方式完成了机床热误差补偿模型的构建，使得热误差补偿模型精度较高且预测结果更加准确。林献坤[9]等应用激光干涉仪测量进给轴的热变形，使用热像仪测量关键点的温度变化，建立基于潜变量回归的热误差识别模型，该模型可将热误差减小75%。针对主轴系统温升测试过程中测点呈离散分布的特点，所采集温升数据无法覆盖主轴系统温度场的全部信息，数据具有小样本、贫信息的缺点，张伟[10]等将灰色系统理论与模糊聚类方法应用于机床主轴热误差模型构建。马驰[11]等基于遗传算法与神经网络模型构建了主轴系统轴向热伸长与径向热倾角误差模型，并对该误差补偿模型进行了预测分析。杨军[12]等通过建立主轴轴向热伸长及径向热倾角的最小二乘支持向量机以及多元线性回归的综合热误差模型，发现最小二乘支持向量机模型具备全局寻优的特点，预测精度可达90%。苗恩铭[13]等采用支持向量回归机与多元回归建模方法构建了机床主轴热误差模型并进行了对比分析，发现支持向量回归机模型用于热误差补偿具有较高精度且鲁棒性较好。

然而，上述方法都有其局限性，利用回归分析方法构建热误差模型时，往往会构建出超越方程，求解过程复杂，运算收敛性较差。神经网络构建热误差建模时，具有以任意精度逼近函数的能力，但是只有选择了合适的网络结构，才能使精度达到最优，且算法中权值与阀值的初始化具有较大随机性，建模过程中甚至出现过拟合现象，建模效率较低。最小二乘法是一种基于梯度信息的方法，其前提是适应值函数及性能指标可微和搜索空间平滑，在热误差建模应用中，由于获得的数据多呈现非连续性特征，无法满足算法的前提条件。支持向量机具有严谨的理论和数学基础，对样本数量的依赖性弱，且克服了局部收敛问题，但支持向量机的预测性能对参数的选择非常敏感，实际应用中大多凭经验确定参数或采用试算法，易导致由于参数选择不准确使热误差补偿预测精度较低。

粒子滤波重采样粒子群算法(Re-samplingStepParticleSwamOptimization，RSPSO)在标准粒子群算法搜索中后期引入粒子滤波重采样步骤，根据离当前全局最优粒子的距离给粒子赋以权重，复制权重高的粒子，减少权重低的粒子，缩小PSO算法的搜索范围，大大增强了局部的搜索能力，并提升了算法的搜索效率。为避免粒子的同一性，在重采样步骤后，立即执行粒子变异，可增加种群多样性。本文应用五点法[14]测试某型精密数控车床主轴系统轴向热误差E、主轴径向沿Y向热偏转误差θY与主轴径向沿Z向热偏转误差θZ，采用灰色关联分析法完成温升敏感测点的布置，并应用粒子滤波重采样粒子群算法构建精密车床主轴系统热误差补偿模型。同时，将该热误差模型与多元线性回归分析、标准粒子群算法建立的热误差模型进行比较验证，以检验所建立精密机床主轴系统热误差模型的性能。

2　实验原理与方法

2.1实验系统

本文实验用精密数控机床主轴系统结构如图1所示，该机床加工精度为IT5级，重复定位精度为0.2μm，主轴最高转速为6 000r/min。该机床加工过程中切削用量小，切削力相对较小，由切削运动所产生的热量耗散较少，因此不考虑切削运动部件及切屑的热传导影响。

图1　主轴箱及电动机二维结构图

Fig.1Twodimensionalstructuredrawingofheadstockandmotor

基于ISO230-3数控机床的热误差测量标准，搭建精密机床主轴系统热误差测试试验平台，如图2(a)所示，试验系统利用12组磁吸式PT100温度传感器完成主轴电机、轴承、主轴箱箱体等热源点的温度采集，安装温度传感器时，要尽量靠近热源点，安装测点数量尽量多且一定不能少于主轴热源数量，具体如图2(b)所示：T1放置在主轴前轴承上侧壁；T2放置在主轴前轴承右侧壁；T3放置在主轴前轴承下侧壁；T4放置在主轴后轴承上侧壁；T5放置在主轴后轴承右侧壁；T6放置在主轴后轴承下侧壁；T7放置在主轴箱箱体上端中部；T8放置在主轴箱箱体下端基座联接部；T9放置在主轴箱箱体前端中部；T10放置在主轴箱箱体后端中部；T11放置在电机冷却液进油口；T12放置在电机冷却液出油口，温度变送模块为SBWR-ZK1型，采用VarioCAM®hr红外热像仪监测主轴箱整体温度变化。在主轴径向与轴向安装5个德国米铱公司生产的ILD2200-2型高精度激光位移传感器，用来完成精密机床主轴热误差的测试，激光位移传感器的参数如表1所示。通过信号控制器，NI数据采集系统与Labview数据采集软件采集温度传感器与位移传感器的数据。

(a)试验数据采集平台

(b)温度测点分布

线性量程/mm量程起点/mm量程终点/mm工作温度/℃绝对误差/μm分辨率/μm测量频率/kHz2～5024260～501动态:0.03静态:0.007510

2.2热误差测试原理

(1)

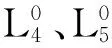
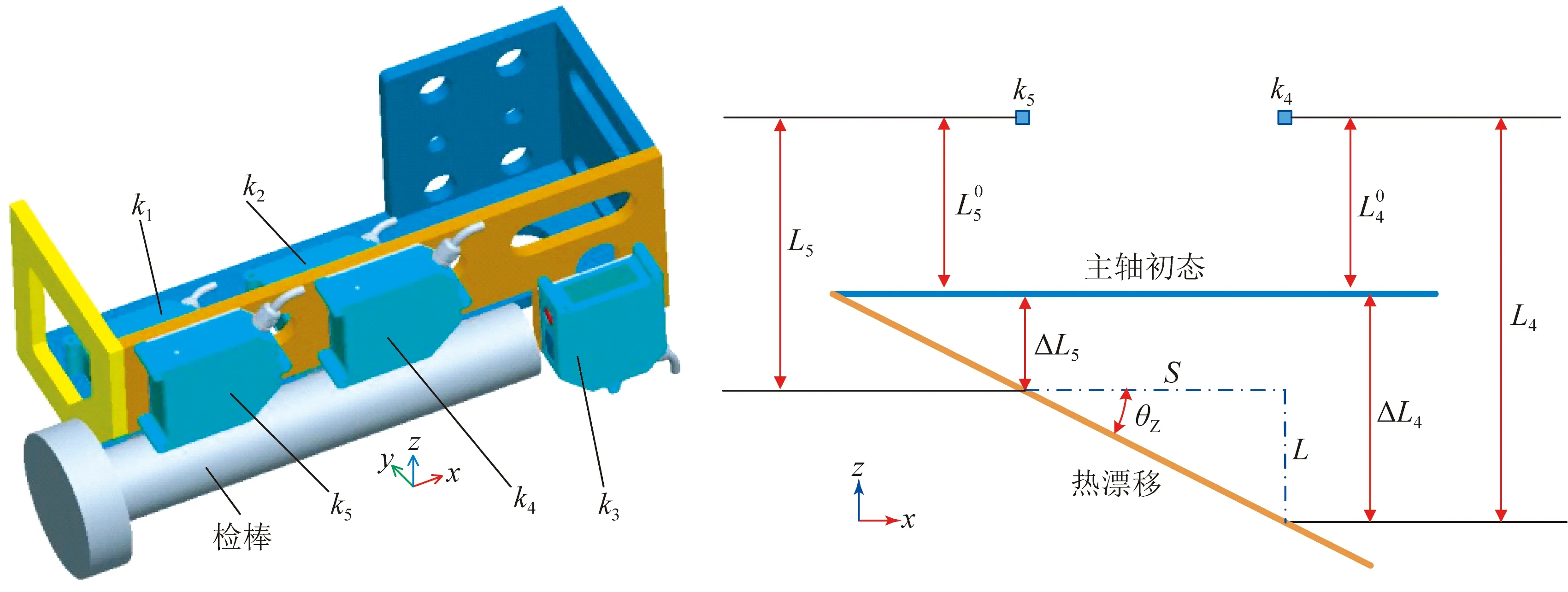
图3　热误差测试原理示意图

2.3实验方法

为了保证测试数据的可靠性，实验过程中共对样机主轴系统开展了3次重复性热误差数据测试试验，且精密数控机床每次实验前12h内都不允许开机。测试室内保持恒温24 ℃，机床表面反射温度为23 ℃，表面热反射率为0.92。测试用检棒由工具钢根据JB/T9981-99标准精密磨削制备，其尺寸参数为Ф45mm×300mm。机床主轴系统安装检棒并在空载状态下以3 000r/min恒速连续运行15min热机，而后持续采集数据4h，且温度传感器测试系统的采样时长为3min，热误差采样时长为1min。同时，采用VarioCAM®hr红外热像仪同步测试数控机床主轴系统温度场及温升变化规律。

3　热误差测试结果分析

分析3组实验测得的热误差数据发现，各激光位移传感器的测试数据宏观上均呈现出先快速变化后趋于平稳恒定的极为相似的分布状态。采用4.1节介绍灰色绝对关联分析方法对各激光位移传感器测试的3组数据序列进行相似度计算，发现数据序列间灰色绝对关联度较大，数据序列相似程度很高。可见在相同实验环境与条件下，机床热误差实验数据测试可靠性较高。以第1组实验测试热误差数据为建模、预测数据开展精密数控车床主轴热误差模型的建立。

图4(a)为主轴系统的热误差分布图，由图可见，随着机床运转时间的递增，主轴沿x轴向的窜动较大，发生了热膨胀现象，主轴轴向热误差在前25min内增速较快，而后缓慢递增并在100min后进入热平衡状态，轴向热误差最大值为13.24μm。k1、k2、k4与k5号激光位移传感器所测得的结果均为正值，表明在YZ平面内，主轴沿负Y与负Z方向发生了热漂移。经k1与k2传感器测试，主轴热误差沿负Y方向也出现了前25min内快速递增，随后进入热平衡状态的现象，且较稳定的最大热漂移量为7.11μm，主轴在XY平面内沿负Y方向偏摆，产生热偏转角θY，即热偏转误差θY。k4与k5传感器测试结果显示，主轴沿负Z方向的热误差在主轴运转50min后进入热平衡状态，且在k4测点出现了热误差先递增、后递减并最终达到热平衡的现象，其最大热漂移量为9.11μm，平衡态最大热误差为8.86μm，主轴在XZ平面内沿负Z方向偏摆，产生热偏转误差θZ。精密车床的加工精度为3～10μm，测试结果显示误差值已超出设计允许精度范围，故必须对机床主轴系统采取热误差补偿措施。

热偏转误差的测试原理如图3(b)所示，且检棒总长为300mm，k1、k2及k4、k5传感器间距S均为120mm。如图4(b)为热偏转误差θY与θZ随主轴运转时间的变化曲线。由图可见，偏转误差θZ整体大于θY，θY与θZ都呈初始递增、后递减并再上升直至热平衡的分布趋势，θY在140min时，偏转误差达到最大，为26.9×10-6°，θZ在70min时，偏转误差达到最大，为37.56×10-6°，并在160min后实现稳定。

由热像仪测试知，机床试验时的环境温度接近24 ℃，主轴系统温度场分布与各测点温升变化规律如图4(c)所示。该精密主轴系统空载运行温升在24～30 ℃内波动，温升区间的变化范围较小。随着空载转动时间递增，主轴上各测点的温度升高，且各测点温升曲线的变化趋势大体相同。与电动机输出轴相连的主轴后端部轴承由于受载较大、电机热量传递且处于封闭箱体内及后端轴承冷却环境较差等原因，导致该轴承温升(T4、T5、T6)速率较快，当主轴系统运行150min后进入热平衡状态时，该轴承最大温升维持在29.3 ℃。主轴前端轴承在进入热平衡状态后，其温度(T1、T2、T3)维持在26.8 ℃。最低测点温度(T11)出现在电机冷却液进油口处，该测点温升在26.5 ℃达到热平衡状态。同时，主轴箱箱体下端基座联接部测点(T8)温升也较为缓慢，在100min左右即进入了热平衡状态。这主要由于主轴箱内部结构、箱体下端部壁厚、联接部热传递导致该测点热量耗散量较大，这与热像仪所观测到的主轴系统热场分布状态相吻合。

(a)主轴热漂移误差

(b)主轴热偏转误差

(c)测点温升变化

4　温度敏感测点辨识策略

温度测点辨识策略是指通过选择最佳测温位置及数目，实现机床主轴系统热误差模型与温度场特性的描述，从而避免温度变量过多引起的所建立热误差模型鲁棒性较差问题。灰色系统理论是一种面向少数据、贫信息的不确定问题数学方法，其计算结果可以充分体现研究系统变量间的关系与规律。为了寻找引起热误差的敏感热源点，本文应用灰色关联分析模型实现温度敏感测点的辨识。

4.1灰色关联分析理论

灰色关联分析理论[15]根据序列曲线几何形状的相似程度来判断序列间联系的紧密程度，即曲线越接近，相应序列之间的关联度越大，反之越小。用灰色关联度来定义数据序列间的关联程度，目前灰色关联度计算方法主要包括灰色绝对关联度计算、灰色相对关联度的计算和灰色综合关联度的计算。通常灰色绝对关联度只体现数据序列间的相似程度，即折线序列的相似程度，而不考虑其他因素；灰色相对关联度则表征了各数据序列相对于起始点的变化速率之间的关系；而灰色综合关联度既体现了折线序列间的相似程度，又反映了序列数据相对于起始点的变化速率的接近程度，是较为全面地表征序列之间联系是否紧密的数量指标[16]。

(1)温度测试数据无量纲处理

在进行温度测试数据量化分析之前，需通过灰算子运算，实现不同量纲或不同数量级数据的归一化处理，无量纲化处理算子主要包括：

1)初值化算子

Ti(k)di=Ti(k)/Ti(1).

(2)

2)均值化算子

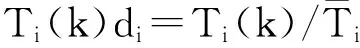
(3)

3)区间化算子

(4)

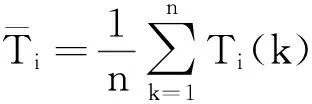
(2)温度变量灰色关联度计算方法

1)灰色绝对关联度

温度传感器测试温度变量经初值化算子无量纲处理后，两组温度变量间的灰色绝对关联度可表示为：

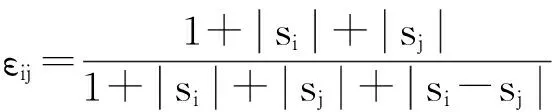
(5)

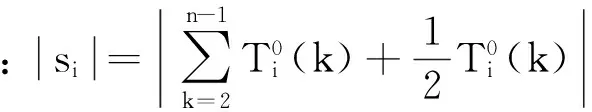
2)灰色相对关联度

温度传感器测试温度变量经均值化算子无量纲处理后，两组温度变量间的灰色相对关联度可表示为：

(6)

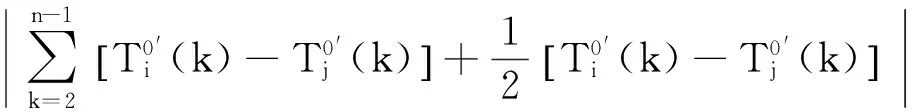
3)灰色综合关联度

温度传感器测试温度变量经区间化算子无量纲处理后，两组温度变量间的灰色综合关联度可表示为：

ρij=ψεij+(1-ψ)γij，

(7)

4.2温度测点灰色综合关联聚类

由于灰色综合关联度计算方法是灰色绝对关联度与灰色相对关联度的综合应用，可更加有效地实现温度变量间的关联特性，因此建立各传感器温升变量数据之间的关联矩阵如表2 所示。选用0.95作为温度变量聚类的相关系数，则温度测点聚类可划分为5组，即T1、T2、T3、T9为第Ⅰ组，T4、T5、T6、T10为第Ⅱ组，T7、T8为第Ⅲ组，T11为Ⅳ组，T12为第Ⅴ组。

表2　温升测点序列综合关联度矩阵

经激光位移传感器测试，机床主轴的最大热漂移误差E出现于沿坐标X方向的主轴轴向上，因此可在各温度变量灰色综合关联度聚类划分的基础上，计算各温度变量与轴向热漂移误差E之间的绝对关联度。计算结果如表3所示。在各聚类组中选择关联度最大测点作为该组温度敏感测点，最终确定的机床主轴系统的轴向热漂移误差E温度敏感点为T1、T4、T7、T11与T12。同理，确定热偏转误差θY温升敏感点为T2、T5、T8、T11与T12，热偏转误差θZ温升敏感点为T1、T6、T8、T11与T12。

表3轴向热漂移误差E温度测点聚类分组

Tab.3ClusteringgroupingoftestedpointsofaxialthermaldrifterrorE

聚类组别Ⅰ组Ⅱ组Ⅲ组Ⅳ组Ⅴ组绝对关联度最大值0.90240.92720.54870.68360.5348温度敏感测点T1T4T7T11T12

表4热偏转误差θY温度测点聚类分组

Tab.4Clustering grouping of tested points of thermal deflection errorθY

聚类组别Ⅰ组Ⅱ组Ⅲ组Ⅳ组Ⅴ组绝对关联度最大值0.92330.90700.60010.64720.6623温度敏感测点T2T5T8T11T12

表5　热偏转误差θZ温度测点聚类分组

5　热误差建模

5.1粒子群建模

(8)

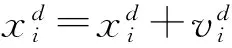
(9)

5.2粒子滤波重采样方法

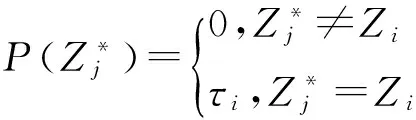
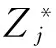
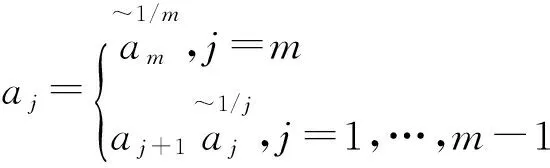
(10)

5.3粒子滤波重采样粒子群算法

在PSO算法进化中后期，收敛速度变慢，在搜索中后期引入粒子滤波重采样步骤，其逻辑是强调算法搜索中后期的局部搜索能力，因此根据粒子与当前全局最优粒子的距离给其赋以权重，粒子滤波重采样步骤可以用来复制权重高的粒子，减少权重低的粒子，从而缩小了PSO算法的搜索范围，大大增强了局部搜索能力，并相应地提升了算法的搜寻效率。为了避免粒子的同一性，在重采样步骤后，立即对已有的粒子执行变异方法，以增加种群的多样性。将改进的PSO算法称为粒子滤波重采样粒子群算法，算法具体步骤如下。

步骤1：初始化粒子群。

(a) 设定恒定参数。粒子群规模为N，惯性权重为ω，加速系数为c1，c2，粒子速度边界为[vmin，vmax]，选择重采样频率δ，即每δ步进行一次重采样。

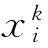
步骤2：若k≥k1(k1为预定迭代步数)，即算法进入搜索中后期，执行步骤3；否则执行步骤6。

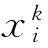
i=1，2，…，N.

(11)

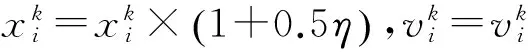
步骤7：如果算法满足终止条件，那么停止，并且输出全局最优位置gBestk+1；否则k=k+1，返回步骤2。

5.4精密车床主轴热误差建模

多元线性回归常用于多变量间实验结果的数学模型的建立，其最关键的问题是对多个参数的估计。多元线性回归方法是最常用的机床主轴系统热误差补偿建模方法，然而该方法在进行参数估计过程中，往往需根据实验测试数据，联立构建超越方程，求解过程异常复杂，常规的迭代算法不易求解，且运算收敛性较差，甚至不收敛。本文应用粒子滤波重采样粒子群算法进行精密数控机床主轴系统的热误差回归模型参数估计研究。

以传感器测试机床主轴系统的轴向热漂移误差E作为因变量，温度敏感点T1、T4、T7、T11、T12的测试温升数据ΔT1、ΔT4、ΔT7、ΔT11、ΔT12作为回归变量，建立热误差E的回归模型，如式(12)所示：

E=β0+β1ΔT1+…+βDΔTD+ε，

(12)

其中：E为因变量，即热漂移误差测试数据；ΔTi为回归变量，即温度敏感点的温升测试数据，且k为各温度敏感点对应的温度传感器序号，且1≤k≤D=12；βk为回归参数，且要求轴向热漂移E与回归参数β具有线性关系；ε为随机误差项，即不可观测的随机变量，且εk相互独立，ε～N(0，σ2)。

将式(12)中的一组回归参数βk作为一个粒子，种群中的每一个粒子代表参数估计问题中的一个解，则第k个粒子可表示为：

βk=(βk，0，βk，1，βk，2，…βk，D).

(13)

定义适应度函数P(ζ)如式(14)所示，其中k=1，2，…，80。

(14)

则适应度函数P(ζ)最小粒子即为最优回归参数。在粒子滤波重采样粒子群算法求解过程中，种群大小N=30；迭代次数为1 000；惯性权重wmax=0.9，wmin=0.4；学习因子c1=c2=2。经RSPSO算法求得的主轴轴向热漂移E回归模型的参数估计值为：

(15)

同理，建立热偏转误差θY与热偏转误差θZ的热误差模型，其回归模型的参数估计值分别为：

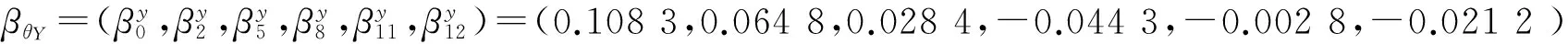
(16)

(17)

则综合热误差模型为：

E=2.731 5ΔT1-0.053 9ΔT4+1.424 6ΔT7-2.280 1ΔT11+0.637 1ΔT12+1.603 7，

θY=0.064 8ΔT2+0.028 4ΔT5-0.044 3ΔT8-0.002 8ΔT11-0.021 2ΔT12+0.108 3，

(18)

θZ=-0.084 4ΔT1+0.210 2ΔT6-0.019 2ΔT8-0.000 2ΔT11-0.016 1ΔT12+0.118 5.

5.5热误差模型评估与预测

分别采用RSPSO算法、标准PSO算法、回归分析法进行热误差模型参数估计运算，使用复测定系数指标R2来评估热误差模型的拟合优度，其计算公式为：

(19)

为了验证RSPSO热误差补偿模型预测精度，采用均方根误差值、预测精度作为评价指标，如式(20)、式(21)所示，其误差补偿模型精度如表6所示。RSPSO热误差补偿模型的仿真输出结果与实验测试数据的对比及残差值分布状态如图5所示。经15 min热机后，激光位移传感器采集的原始实验测试数据与热误差数学模型的预测数值拟合较好，残差较小，机床主轴系统空载连续运行4 h后，各向热误差建模精度均在90%以上，故通过RSPSO热误差补偿模型对机床主轴系统进行热补偿可在很大程度上提高机床的加工精度。

(20)

(21)

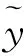
(a)轴向误差E热误差模型预测

(b)热偏转误差θY热误差模型预测

(c)热偏转误差θZ热误差模型预测

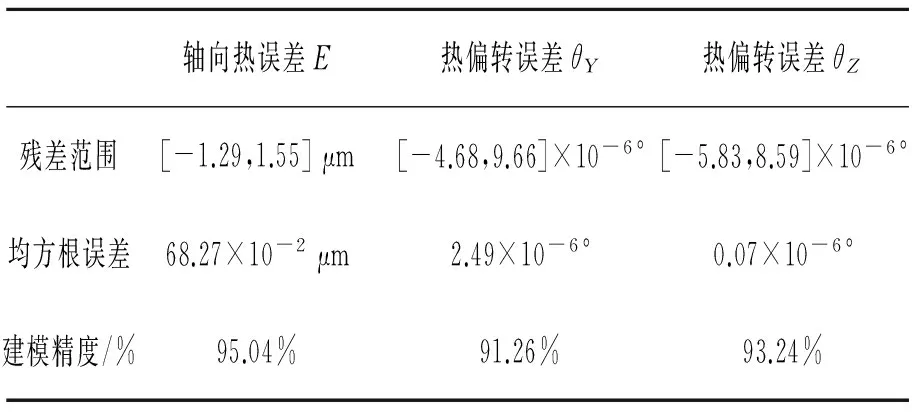
轴向热误差E热偏转误差θY热偏转误差θZ残差范围[-1.29,1.55]μm[-4.68,9.66]×10-6°[-5.83,8.59]×10-6°均方根误差68.27×10-2μm2.49×10-6°0.07×10-6°建模精度/%95.04%91.26%93.24%

6　结　论

本文利用五点法实现了精密数控车床主轴系统轴向热误差与径向热偏转误差测量。主轴系统运行100 min后进入热平衡状态，主轴轴向最大热误差为13.24 μm，负Y方向最大热漂移7.11 μm，负Z方向最大热漂移8.86 μm。考虑到少数据、贫信息的灰色关联分析计算方法可有效地进行温度敏感测点的辨识，将关键测点温度变量由12个减少为各误差补偿模型的5个。从而减小了温度测点的冗余，提升了热误差补偿模型的鲁棒性。鉴于粒子滤波重采样粒子群算法局部搜索能力强收敛速度快的特点，应用RSPSO算法进行精密数控车床主轴系统热误差回归模型参数估计求解。所建立RSPSO热误差补偿模型预测值与实验测试值的拟合精度达90%以上，且残差较小。

空载运行下的精密机床主轴系统热误差测量与补偿是精密机床应客户需求进行机床精度检测与校核的必备环节，这对于提高机床整机精度意义重大。然而，精密机床主轴系统热误差在实际工况中极为复杂，且主轴热误差补偿模型对实验样本又具有较强的依赖性，随着环境温度(冷却液质量、散热与隔热系统)、机床工作状态(空载、负载、重载)、加工工艺(进给量、切削速度、背吃刀量)等实际工况与测试条件的变化，所建立的热误差补偿模型也随之改变，可否针对精密数控车床主轴系统建立具有一定运行环境适应性与泛化能力的热误差补偿模型将是后续研究的重点。

[1]RAMESH R， MANNAN M A， POO A N. Error compensation in machine tools-a review part Ⅱ：thermal error[J].InternationalJournalofMachineToolsandManufacture， 2000， 40(9)：1257-1284.

[2]JOSEF M， JERZY J， ECKART U，etal.. Thermal issues in machine tools[J].CIRPAnnalsManufacturingTechnology， 2012， 61(2)：771-791.

[3]王海同，李铁民，王立平，等.机床热误差建模研究综述[J].机械工程学报，2015， 51(9)：119-128.

WANG H T， LI T M， WANG L P，etal.. Review on thermal error modeling of machine tools[J].JournalofMechanicalEngineering， 2015， 51(9)：119-128.(in Chinese)

[4]张成新，高峰，李艳，等.基于分段拟合的机床大尺寸工作台热误差补偿模型[J].机械工程学报，2015， 51(3)：146-152.

ZHANG CH X， GAO F， LI Y，etal.. Model of thermal error compensation of large size worktable for machine tools based on piecewise fitting [J].JournalofMechanicalEngineering， 2015， 51(3)：146-152.(in Chinese)

[5]要小鹏，殷国富，李光明. 基于OE-CM算法的机床主轴热误差建模与补偿分析[J].中国机械工程，2015， 26(20)：2757-2762.

YAO X P， YIN G F， LI G M. Thermal error modeling and compensation analysis based on OE-CM algorithm for machine tool spindles [J].ChinaMechanicalEngineering， 2015， 26(20)：2757-2762.(in Chinese)

[6]王乾俸，张松，陈舟，等. 基于指数函数的机床主轴热误差补偿模型[J].计算机集成制造系统， 2015， 21(6)：1553-1558.

WANG Q F， ZHANG S， CHEN ZH，etal.. Thermal error compensation model of machine spindle based on exponential function[J].ComputerIntegratedManufacturingSystems， 2015， 21(6)：1553-1558.(in Chinese)

[7]朱小龙，杨建国，代贵松. 基于AVQ聚类和OIF-Elman神经网络的机床热误差建模[J].上海交通大学学报，2014， 48(1)：16-21.ZHU X L， YANG J G， DAI G S. AVQ clustering algorithm and OIF-Elman neural network for machine tool thermal error [J].JournalofShanghaiJiaoTongUniversity， 2014，48(1)：16-21.(in Chinese)

[8]陈诚，杨传民，张晨阳，等.考虑运行条件的Elman网络丝杠驱动系统热误差建模[J].光学 精密工程， 2014，22(3)： 704-711.

CHEN CH， YANG CH M， ZHANF CH Y，etal.. Modeling on thermal errors of ball screw driving system on Elman network considering operating conditions [J].Opt.PrecisionEng.， 2014，22(3)： 704-711.(in Chinese)

[9]林献坤，王益涵，朱琳.应用潜变量回归在线补偿双直接进给轴热误差[J].光学 精密工程， 2015，23(2)：430-437.

LIN X K， WANG Y H， ZHU L. Online compensation of thermal error for dual direct feed drive system with latent variable model [J].Opt.PrecisionEng.， 2015，23(2)： 430-437.(in Chinese)

[10]张伟，叶文华.基于灰色关联和模糊聚类的机床温度测点优化[J].中国机械工程，2014，25(4)： 456-460.

ZHANG W， YE W H. Optimization of temperature measuring points for machine tools based on grey correlation and fuzzy clustering analysis [J].ChinaMechanicalEngineering， 2014， 25(4)：456-460.(in Chinese)

[11]马驰，杨军，梅雪松，等.基于遗传算法及BP网络的主轴热误差建模[J].计算机集成制造系统，2015，21(10)：2627-2636.

MA CH， YANG J， MEI X S，etal.. High-speed spindle thermal error modeling based on genetic algorithm and BP neural network [J].ComputerIntegratedManufacturingSystems， 2015， 21(10)：2627-2636.(in Chinese)

[12]杨军，梅雪松，赵亮，等.基于模糊聚类测点优化与向量机的坐标镗床热误差建模[J].上海交通大学学报，2014， 48(8)：20-28.

YANG J， MEI X S， ZHAO L，etal.. Thermal error modeling of a coordinate boring machine based on fuzzy clustering and SVM [J].JournalofShanghaiJiaoTongUniversity， 2014， 48(8)：20-28.(in Chinese)

[13]苗恩铭，龚亚运，成天驹，等.支持向量回归机在数控加工中心热误差建模中的应用[J].光学 精密工程，2013，21(4)：980-986.

MIAO E M， GONG Y Y， CHENG T J，etal.. Application of support vector regression machine to thermal error modelling of machine tools [J].Opt.PrecisionEng.， 2013，21(4)：980-986.(in Chinese)

[14]仇健，刘春时，刘启伟，等.龙门数控机床主轴热误差及其改善措施[J].机械工程学报， 2012， 48(21)：149-157.QIU J， LIU CH SH， LIU Q W，etal.. Thermal errors of planer type NC machine tools and its improvement measures [J].JournalofMechanicalEngineering， 2012， 48(21)： 149-157.(in Chinese)

[15]刘思峰，党耀国，方志耕，等. 灰色系统理论及其应用[M]. 第5版， 北京： 科学出版社， 2010.

LIU S F， DANG Y G， FANG ZH G，etal..GraySystemTheoryandItsApplication[M]. 5thed. Beijing： Science Press， 2010.(in Chinese)

[16]董菲菲，罗贤运，吕保和.天然气管道内腐蚀影响因素的灰色综合关联度分析[J].安全与环境学报，2014，14(5)：15-18.

DONG F F，LUO X Y，LV B H.Analysis of impact factors of natural gas pipeline internal corrosion based on the grey comprehensive correlation [J].JournalofSafetyandEnvironment，2014，14(5)：15-18.(in Chinese)

[17]CLERE M， KENNEDY J. The particle swarm-explosion， stability and convergence in multidimesional complex space [J].IEEETransactionsonEvolutionaryComputation， 2002， 6(1)：58-73.

[18]WAI R， LEE J， CHUANG K. Real-time PID control strategy for maglev transportation system via particle swarm optimization [J].IEEETransactionsonIndustrialElectronics， 2010， 58(2)：629-646.

[19]SHARMA K D， CHATTERJEE A， RAKSHIT A. A hybrid approach for design of stable adaptive fuzzy controllers employing lyapunov theory and particle swarm optimization[J].IEEETransactionsonFuzzySystems， 2009， 17(2)： 329-342.

[20]KARANKI S B， MISHRA M K， KUMAR B K. Particle swarm optimization based feedback controller for unified power quality conditioner [J].IEEETransactionsonPowerDelivery， 2010， 25(4)：2814-2824.

郭辰光(1982-)，男，辽宁朝阳人，博士，讲师，2005年于沈阳建筑大学获得学士学位，2008年、2011于东北大学分别获得硕士、博士学位，主要从事高档数控机床及自动化技术方面的研究。E-mail： gchg_neu@163.com

韩雪(1990-)，女，辽宁本溪人，硕士，2012年、2016于辽宁工程技术大学分别获得学士、硕士学位，主要从事智能控制与优化算法研究。E-mail： hanxue.boda@163.com

(本栏目编辑：马健)

(版权所有未经许可不得转载)

Thermal error modeling for spindle system of precision CNC lathe

GUO Chen-guang1，2*， HAN Xue1， LI Yuan1， XIE Hua-long2

(1. College of Mechanical Engineering， Liaoning Technology University， Fuxin 123000， China；2. Institute of Advanced Manufacturing and Automation Technology，Northeastern University， Shenyang 110819， China)

*Corresponding author， E-mail：gchg_neu@163.com

TheexperimentsandmodelingofthermalerrorcompensationforthespindlesystemofaComputerNumericalControl(CNC)lathewereresearched.AthermalerrorcompensationmodelfortheSpindlesystemofCNClatheataxialandradialdirectionswasestablishedtoenhanceitserrorcompensationabilityandtoimprovethemachiningprecision.Atestplatformforthethermalerrorofthespindlesystemwasbuilt.Thefivepointmethodwasusedtotestthethermalerrorofthespindlesystem,andathermocoupleandainfraredthermalimagerweretakentomeasurethetemperaturechangesofthespindlesystem.Thenthegraycomprehensivecorrelationanalysismethodwasusedtoidentifythetemperature-sensitivemeasurementpointsandtoconstructthermalerrorpredictionmodelbasedonre-samplingstepparticleswamoptimizationtoevaluatethemodeleffect.Thepredictionresultsonthethermalerrorcompensationmodelbasedonre-samplingstepparticleswamoptimizationshowthattheaxialresidualthermalerroris-1.29μm—1.55μm,andthemodelingaccuracyis95.04%.Thethermalresidualerroralongydirectionis-4.68×10-6°—9.66×10-6°,andthemodelingaccuracyis91.26%.Thethermalresidualerroralongzdirectionis-5.83×10-6°—8.59×10-6°,andthemodelingaccuracyis93.24%.Theresearchshowsthatthethermalerrorcompensationmodelhashighprecisionandastrongengineeringapplicationvalue.

precisionComputerNumericalControl(CNC)lathe;spindlesystem;thermalerrormodeling;thermalerrorcompensation;Re-samplingStepParticleSwamOptimization(RSPSO)

2016-01-26；

2016-03-31.

国家“十二五”科技支撑计划资助项目(No.2012BAF12B08)；国家自然科学基金资助项目(No.51475087)；辽宁省科技计划项目(No.20131043)；辽宁省煤矿液压技术与装备工程研究中心开放课题基金资助项目(No.CMHT-201208)

1004-924X(2016)07-1731-12

TG502.15；TG659

Adoi:10.3788/OPE.20162407.1731