非金属管道损伤的非线性超声导波延时检测定位方法
洪晓斌,冯进亨,林沛嵩,刘桂雄
(华南理工大学 机械与汽车工程学院,广东 广州 510640)
非金属管道损伤的非线性超声导波延时检测定位方法
洪晓斌,冯进亨,林沛嵩,刘桂雄*
(华南理工大学 机械与汽车工程学院,广东 广州 510640)
由于超声导波难以准确检测非金属管道的早期损伤,本文提出了一种非线性超声导波延时方法对非金属管道结构损伤进行测试和定位。基于非线性超声调制机理分析了非金属管道损伤状态,使用同侧非线性超声的混频信号激励方式并根据超声导波传播速度的差异产生激励信号延时,然后在管道损伤处实现混频信号的非线性调制。采用HHT(Hilbert-HuangTransformation)提取混频延时信号的瞬时特征量,并通过分析非线性分量延时分组进行损伤区域检测,实现了对非金属管道裂纹损伤的定位。PVC(Ployninylchloride)非金属管道实验显示,无损伤状态下延时信号分组的标准化基准值为0.518 8;单裂纹状态下延时信号分组标准值为0.593 7,损伤定位相对误差为3.277%;双裂纹损伤状态下的标准化瞬时平均幅值为0.580 1与0.607 3,损伤定位值绝对误差小于4mm。相对于利用小波包络分解的非线性延时定位检测法,实验得到的单裂纹损伤准确度提高了36.4%。结果表明该方法能够对非金属管道裂纹损伤准确定位,并能够检测早期多裂纹损伤。
非金属管道;损伤定位;超声导波延时检测法;非线性调制
1 引 言
非金属管材具有强度高、密度小、腐蚀性强、绝缘性优、使用寿命长等优点,在石化行业、建筑业、市政工程、农业等领域需求不断加大,促使非金属管道得到快速发展[1]。近年来,非金属管道结构损伤检测研究发展迅速,主要集中在非金属管材的直型管道、管道接头等结构。加拿大达尔豪斯大学N.Cheraghi与M.J.Riley采用压电陶瓷对于非金属管道的接头连接处损伤进行研究[2];法国里昂中央理工学院O.Bareille与M.Kharrat设计扭转模态导波探头研究了非金属管道导波响应特性与损伤特性[3];意大利罗马大学P.Annamaria通过高斯脉冲导波激励对非金属圆棒上凹槽损伤进行了仿真与实验研究[4];法国巴黎高科矿业学院L.Laiarinandrasana通过研究非金属管道上损伤的蠕变效应预测了管道剩余寿命[5]。由于超声导波具有长距离检测、隐蔽区域检测、灵敏度高、实施方便等优点,在非金属管道结构损伤检测中得到了广泛关注,但其在非金属管材上存在衰减快、传播速度低等特点,使得当前所研究非金属管道损伤类型主要针对损伤占管道轴向与径向区域较大,而针对非金属管道上的早期损伤检测方法研究较少,因此亟需对非金属管道早期微小损伤有效超声导波检测技术进行探究。
在材料非线性理论中,应力波在非线性材料上传播会产生高次谐波,多个应力波传播则会互相影响产生调制作用。由于损伤具有材料非线性特性,混频超声导波的非线性效应对微小缺陷具有较好的敏感度,更有利于早期管道健康监测。非线性超声调制检测原理近年来得到快速发展,美国西北大学M.H.Liu根据超声共振调制方法得到压缩变形构件的非线性系数[6];韩国科学技术院H.Sohn针对非线性超声分量小且难以提取,提取通过减去对不同激励超声信号的单独接收信号来获得非线性分量[7];美国俄亥俄州立大学G.D.Connolly通过多次非线性超声信号在金属裂纹缺陷上多次采集,使用数值识别技术达到非线性信号有效提取与增强信噪比[8];哈尔滨工业大学刘斌等使用振动声调制技术对复杂结构焊缝缺陷实现检测[9]。目前非线性超声导波技术在金属结构损伤中研究较多,包括增强非线性信号信噪比、结构损伤非线性系数获取等,但仍未见面向非金属管道的超声非线性调制检测技术研究。本文采用同侧非线性超声混频激励法,对非金属管道裂纹损伤进行检测,结合加载到混频信号中的延时时间,对非金属管道损失进行损伤定位研究。
2 非金属管道损伤非线性超声延时检测定位方法提出
非线性超声导波调制技术,利用低频信号对高频信号实现调制,若在线性介质中传播,并不产生非线性调制现象;而由于材料内部损伤(如裂纹等)具有非线性特性,有利于损伤的检测。根据波动理论所阐述的弹性波非线性运动方程,一个双通道混频信号超声激励后经过损伤后所获取信号为:
u(x,t)=u(0)+βu(1)=
A01cos(ω1τ)+A02cos(ω2τ)+

(1)
式中:信号1与信号2幅值为A01与A02,信号1与信号2角频率为ω1和ω2,β为非线性系数,k1和k2为信号1与信号2的波数。从不同频率分布的角度分析,式(1)中包含原来ω1与ω2的频率,同时有2ω1与2ω2,以及和频ω1+ω2和差频ω1-ω2。通过弹簧模型可知,裂纹的开合产生的位移,与材料的宏观属性,以及裂纹上的力学特性和裂纹形态相关,同时也可以看到非线性超声调制现象。因此,非线性幅值调制现象是在混频信号的作用下,超声导波通过具有非线性特性损伤的非金属管道后能够产生多个不同频率的非线性谐波信号,根据此特性,可建立有利于对非金属管道损伤进行检测的方法。
由于导波在非金属管材上衰减快,传统的超声“回波”检测法难以实现,对于穿透式的混频信号检测方法,损伤信息携带在通过损伤的导波中,优点尤为明显。同时由于导波在非金属传播速度较金属管道低,传播距离短,只在时域上的损伤定位法效果并不理想,利用HHT提取时频特征信息结合非线性调制原理能够在实现检测范围较短的损伤定位。因此提出一种非金属管道损伤非线性超声延时定位检测方法(如图1所示)。采用一种非线性混频激励同侧检测方式,求取管道的导波频散曲线,选取高频与低频信号频率,控制混频信号的激励时间;速度较大者通过增加延时,从而使两通道信号能够在管道上同时到达任意位置,混频信号在损伤处相遇时能够产生的非线性调制分量;各个延时信号进行分组,可以利用HHT,通过EMD(EmpiricalModeDecomposition)提取各组延时的混频信号的非线性分量,利用Hilbert变换得到信号瞬时特征量,瞬时幅值作为损伤评价来选择较大非线性分量对应的组,结合混频信号传播速度,计算出损伤位置。

图1 定位方法框架
3 非金属管道损伤非线性超声延时检测定位新方法实现过程
3.1非线性同侧混频激励检测
非线性超声混频信号同侧激励法如图2所示,为了实现信号在结构损伤处能够产生声调制现象,采用双通道混频激励信号(换能器A激励信号EA(t)、B激励信号EB(t)),单通道接收信号(换能器R接收信号R(t)),同时激励信号可采取正弦周期信号。激励换能器A、B固定在非金属管道一侧,接收换能器R固定同一直线上另一侧,激励换能器A与B之间距离为lAB,接收换能器与激励换能器A的距离为lR。假设裂纹损伤在离激励换能器A的距离为L,结合高频激励信号与低频激励信号不同的传播速度(高频信号速度vA大于低频信号速度vB),可以求出高频信号与低频信号各自到达接收换能器R各自对应的时间为:
tA=lR/vA,
(2)

(3)
混频信号在非金属管道上传播如图3所示,虚线所表示的低频信号传播速度低于实线所表示的高频信号传播速度,通过在高频信号中加载延时时间,混频信号能够实现对管道的扫查,假设混频信号在损伤处相遇(见图3虚线圆)能够产生较强的非线性效应。

图2 混频信号同侧激励示意图

图3 同侧激励混频延时信号传播
同时,为得到更好的非线性调制现象,采用多周期的激励信号,其中高频信号频率fA,低频信号频率fB,即信号周期为TA=1/fA和TB=1/fB。可知导波到达传感器时间需大于信号多个周期时间,假设高频信号周期数为nA,有:
tA>nATA(nA=1,2,3,…).
(4)
同样,设低频信号周期数为nB,得:
tB>nBTB(nB=1,2,3,…).
(5)
可以得到最大延时时间tM应满足:
tM≥tB-tA.
(6)
设加载到高频信号上延时固定步长为ts,总延时次数为Nd(表示总共要激励Nd次混频信号):
Nd=tM/ts.
(7)
可知,每一个高频信号具有按固定延时步长ts的整数倍的td:
td=n*ts(n=1,2,3,…,Nd).
(8)
3.2基于Hilbert-Huang变换的瞬时特征量提取
当损伤存在时,双通道混频信号激励后可获取多分量信号。为了计算瞬时特征量,采用对于多分量信号时域处理方法EMD,可把多分量信号分解成若干单分量IMF(IntrinsicModeFunction)以及剩余函数rn[10],分离得到单分量信号可实现信号特征提取。满足损伤检测的IMF形式:
c(t)=a(t)cosφ(t),
(9)

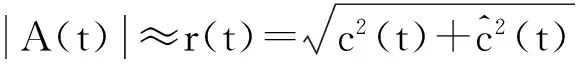
(10)

(11)
3.3基于非线性分量的结构损伤判别
从非线性超声调制特性与损伤关系可知非金属管道损伤程度与非线性损伤分量呈单调增加关系[12]。但由于损伤自身对导波具有衰减作用,尤其在非金属材料更为明显,随着损伤增大到一定程度后,采集信号R(t)幅值随之下降,以致在R(t) 中的非线性损伤分量被大幅减少,影响其单调增加趋势。因此可利用数据标准化补偿对R(t)减小的部分来实现非线性损伤分量有效提取。
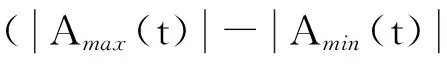
(12)
由于激励信号采用多周期正弦信号可以产生强的非线性效应,另一方面为了提高检测精度则需要单周期正弦信号,因此针对实际所产生的非线性调制效果分为单周期与多周期信号激励损伤评估方法。

(13)


(14)
3.4损伤区域定位
为实现区域损伤定位,需根据最大延时时间tM对所有延时时间进行分组,得延时分组D1,D2,…,Dn,利用上述损伤判别方法从D1,D2,…,Dn损伤所在的组作为DTi(i=1,2,…,n)。如图4,分别对各个DTi进行分组Dk2,…,Dkn(k=2,3,…)表示第k次分组,同样平均分成n个延时组,选出此时损伤所存在的组作为DSi。通过减小加载在高频激励信号的延时步长ts,重复上述步骤直到固定延时ts到达设定精度得到DFi。
根据激励与接收换能器布置求出vA,vB,可知2个信号在非金属管道上某一位置相遇所需的延时时间,设L0为非金属管道上的某一位置,T0为对应L0的延时时间,可得L0与T0的关系:

(15)

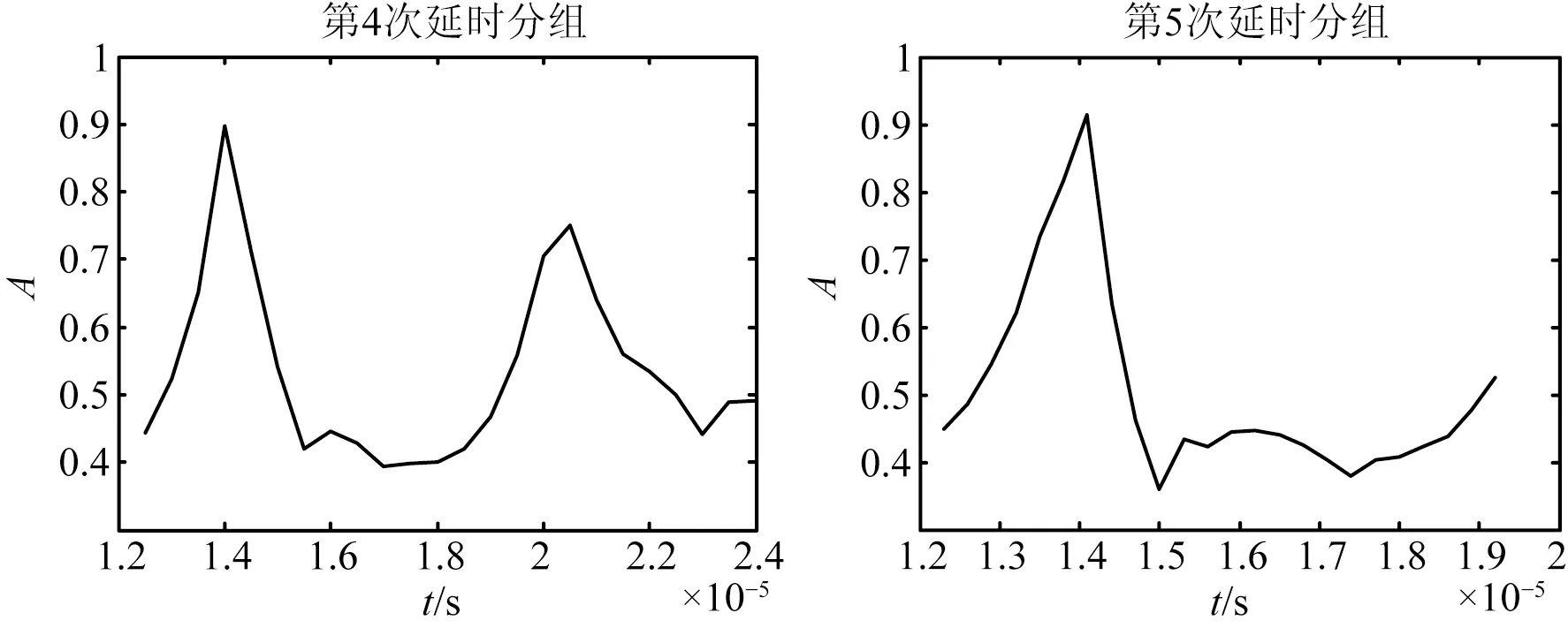
Tmax=A-1(max{A(t1),…,A(tn)})(i=1,2,…,n),
(16)
式中:A-1为A(t)的反函数,max表示取A(ti)最大值。从而得出非金属管道损伤为:

(17)

图4 损伤局部定位流程示意图
4 非金属管道损伤检测实验
4.1实验平台
实验所采用PVC非金属管道材料特性与尺寸参数如表1所示,压电换能器特性如表2所示。

表1 PVC管道参数

表2 压电换能器参数
压电换能器通过环氧树脂胶固定在PVC管道上(如图5所示)。激励换能器A与B之间距离lAB为10mm,接收换能器与激励换能器A距离为lR为70mm。实验设备平台如图6所示,压电换能器激励源A以及压电换能器激励源B与波形发生器相连,同时,压电激励源A与信号放大器A相连,压电激励源B与信号放大器B相连。压电接收换能器R与一个数据采集系统相连接。

图5 换能器在PVC管道上布置示意图

图6 非线性超声损伤检测实验平台示意图
4.2非金属管道无损伤状态实验
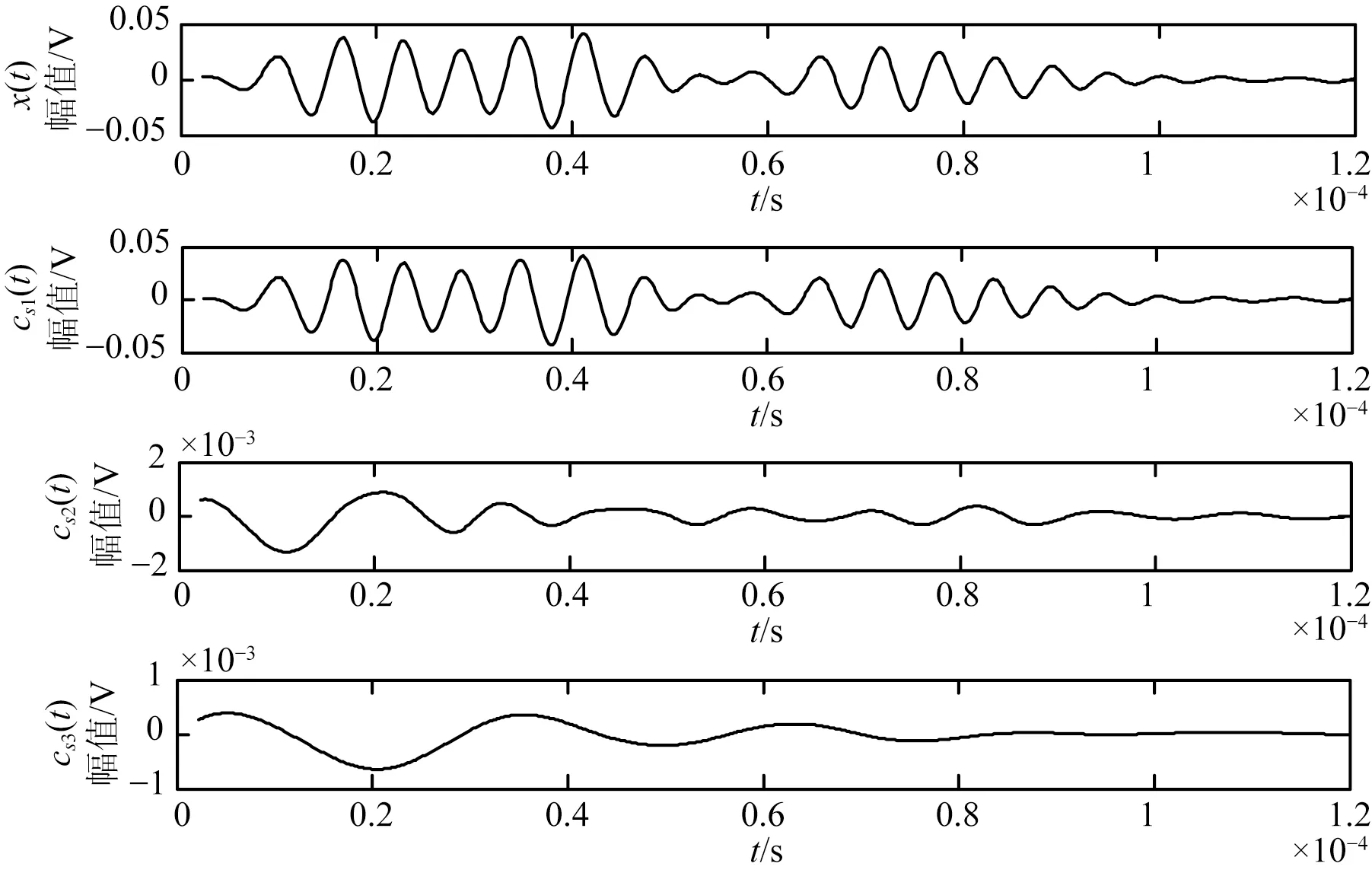
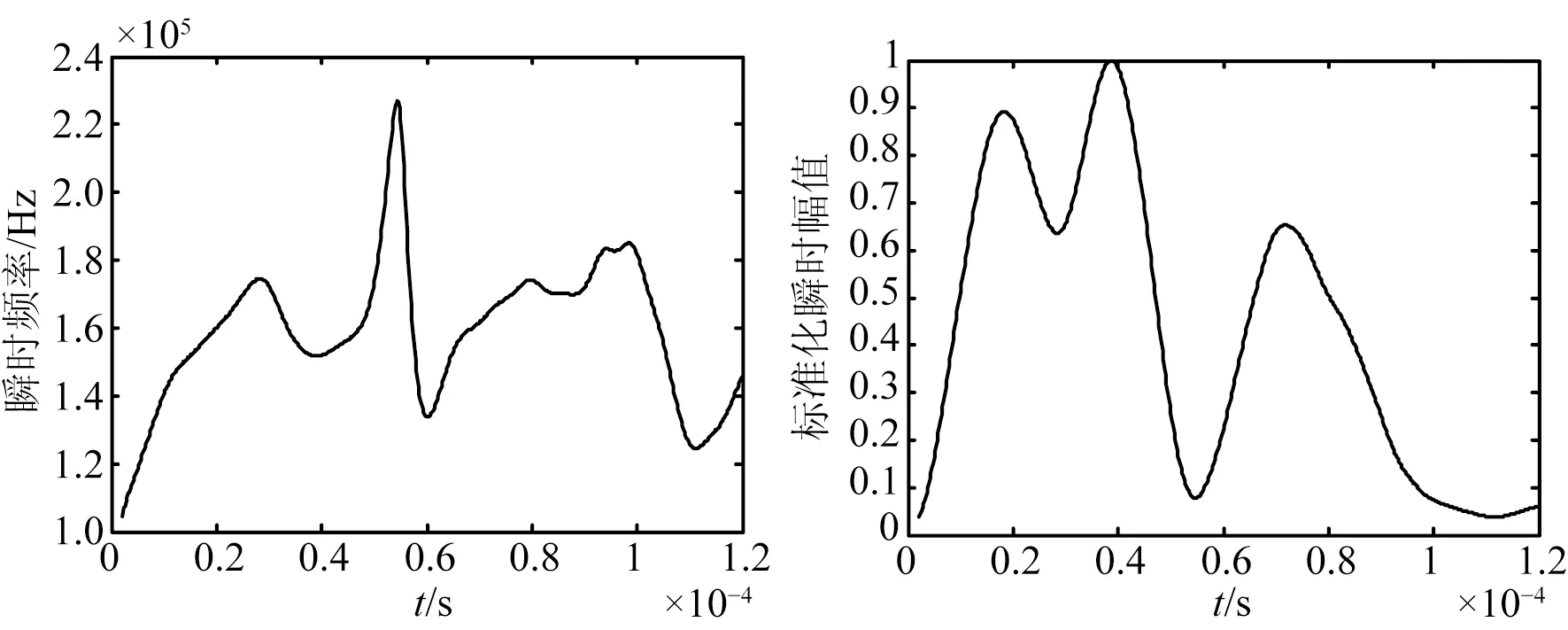
首先对PVC管道进行一发一收频率响应实验,换能器A激励扫频信号频率从100Hz到300kHz,输出峰-峰值为2V,信号进行50倍放大。采集信号通过Fourier变换得到频谱如图7所示。为了增强非线性超声调制现象与符合混频信号传播速度差异,低频信号频率选取为50kHz,高频信号频率选取120kHz,传播速度测量是通过第一个到达传感器的导波信号求得,通过实验得两者传播速度为vA=1 925m/s和vB=1 213m/s,此速度用于计算损伤定位可以避免模态转换产生的影响。根据式(2)~(3)可求出tA=5.19×10-5s,同时求得tB=7.41×10-5s,TA=6.66×10-6s,TB=2×10-5s。由此计算出高频和低频信号最大可以取的周期数,nA 图7 PVC管道频率响应频谱示意图 图8 延时信号EMD分解示意图 D1与D2每一个混频延时信号都需要提取其瞬时特征量,为了可以更好地阐述其信号处理过程,选取延时时间在总延时范围中间部分的信号,这里选择D1中的第9个混频延时信号作为例子解释瞬时特征量提取过程。为了EMD信号分解不会出现较多的模态混叠,采集信号通过频率从80kHz到240kHz带通滤波器,D1中的第9个混频延时信号分解得到的IMF如图8所示,选取包含主要信号及非线性分量的cs1作为c(t)。 通过Hilbert-Huang变换,结合式(10)~(12)求出其瞬时频率与标准化瞬时幅值。对D1中的第9个混频延时信号进行分析,在图9的瞬时幅值图中找出对应非线性分量的170kHz的第一旁瓣的频率,得到t0=2.84×10-5s,从而得到其对应的标准瞬时幅值为0.636 1。 图9 瞬时频率与标准化瞬时幅值示意图 4.3单裂纹损伤检测实验 从图5可知,裂纹到换能器A的实际距离L为70mm。PVC管道单损伤实验保持总延时次数Nd=24,延时信号同样分成两组D1、D2,高频信号120kHz正弦信号,低频信号50kHz正弦信号,最小延时步长ts=3×10-7s。 第1次混频信号分组与无损伤状态下的实验一致,得到组D1的标准化瞬时幅值之和为0.491 9,组D2为0.593 7,满足式(14),可知存在损伤位于组的延时范围内,组D2记为组DS1。 表3 单裂纹检测延时分组参数 图10 单裂纹第2次分组不同延时瞬时幅值分布 Fig.10Instantaneousstandardizedamplitudeof2nddelaysignalgroup 图11 单裂纹第3次分组不同延时瞬时幅值分布 4.4双裂纹损伤检测实验 如图12,第一处裂纹到换能器A的实际距离L2为70mm,设最终测出裂纹定位长度为l2;第二处裂纹到换能器A的距离为L1为27mm,定位估计值设为l1。每次分组分为组D1、D2,总延时信号个数Nd=24,最小延时步长为ts=3×10-7s。采用同样的实验方法,分组实验所用激励信号周期、延时时间、延时步长如表4所示。 图12 双裂纹在PVC管道上位置示意图 延时分组高频信号周期数低频信号周期数延时时间延时步长142[0,2.4×10-5s]1×10-6s221[0,1.2×10-5s]5×10-7s311[0,7.2×10-6s]3×10-7s421[1.2×10-5s,2.4×10-5s]5×10-7s511[1.2×10-5s,1.92×10-5s]3×10-7s 分析第1次延时信号分组D1的标准化瞬时幅值之和为0.580 1,组D2为0.607 3。所以组D1和D2都满足式(14)的条件,即检测到有两个损伤在PVC管道上,所以有D1为DT1,D2为DT2。 图13 双裂纹第2,3次分组不同延时瞬时幅值分布 Fig.13Instantaneousstandardizedamplitudeof2nd, 3rddelaysignalgroup 图14 双裂纹第4,5次分组不同延时瞬时幅值分布 Fig.14Instantaneousstandardizedamplitudeof4th, 5thdelaysignalgroup 4.5方法实验比较 对于常见的基于小波包络分析的非线性超声调制方法使用小波包络[13-14]得到其对应的小波能量值,通过比较各个延时状态下的小波能量值获取较大值时刻来求取裂纹定位估计值。 对图12所示的PVC管道双裂纹损伤,基于小波包分析法得到面向双裂纹PVC管道的高频分量小波能量值如图16所示。取出小波能量值的最大值与次大值,求出其对应的Tmax1=2.4×10-6s,Tmax2=1.44×10-5s,代入公式(17)求出l1=34.907mm,l2=74.262mm。 图16 80个延时信号双裂纹小波能量值 从定位精确度上比较,在同等延时步长的情况下,无论是单裂纹损伤还是双裂纹损伤,基于HHT的管道损伤定位法比小波包络法的结果更精确,单裂纹情况准确度可提高36.4%。从图15可以看到,对于选取哪个延时时刻作为Tmax难度较大,对于双裂纹情况,在整个延时范围内选取最大的小波能量值的难度更大。其相互区别非常小的主要原因是单脉冲激励,带通滤波器与小波包络分析并不能得到最好的分析效果,以及信号时域叠加对信号幅值的影响;对于PVC管道损伤非线性超声伤检测延时新方法,由于采用了多脉冲串激励,对应不同激励方式用不同方法选取延时范围以及使用瞬时特征量作为判别依据,能够较好地解决延时时刻难以确定的问题。 本文提出了一种非线性超声导波延时检测新方法来研究非金属管道早期损伤定位问题。该方法采用同侧混频激励的穿透式检测方法,结合在激励信号加载延时时间使超声导波覆盖整个管道结构。使用HHT变换有效地对混频延时信号进行时频分析,提取混频信号中非线性损伤分量的瞬时特征量,对延时加以分组,从而对延时范围内的有效区域内单裂纹与多裂纹损伤实现检测。尤其在PVC非金属管道结构损伤检测中,相对于小波包络法的检测方法,更容易获取损伤所在延时范围,准确度提高36.4%。同时该方法可进一步拓展到过墙非金属管道、内衬防腐蚀管道界面的损伤检测等,对非金属管道复杂结构健康监测深入研究提供指导作用。 [1]李成吾, 左继成. 国内外PVC技术现状及发展方向[J]. 当代化工,2015(4):711-714.LICHW,ZUOJCH.Technologystatus-quoanddevelopmentdirectionofPVCpipes[J]. Contemporary Chemical Industry, 2015(4): 711-714.(inChinese) [2]CHERAGHIN,RILEYMJ,TAHERIF.Anovelapproachfordetectionofdamageinadhesivelybondedjointsinplasticpipesbasedonvibrationmethodusingpiezoelectricsensors[C]. 2005 IEEE International Conference on Systems, Man and Cybernetics, 2005, 4: 3472-3478. [3]BAREILLEO,KHARRATM,ZHOUW, et al..DistributedpiezoelectricguidedT-Wavegenerator,designandanalysis[C]. 2010 First Workshop on Hardware and Software Implementation and Control of Distributed MEMS, 2010:38-42. [4]PAUA,VESTRONIF.Damagecharacterizationinbarsusingguidedwaves[C]. Proceedings of the XIX AIMETA Congress, Ancona, 2009: 65-75. [5]LAIARINANDRASANAL,GAUDICHETE,OBERTIS, et al..Effectsofagingonthecreepbehaviourandresiduallifetimeassessmentofpolyvinylchloride(PVC)pipes[J]. International Journal of Pressure Vessels & Piping, 2011, 88(2-3):99-108. [6]LIUM,TANGG,JACOBSLJ, et al..Measuringacousticnonlinearitybycollinearmixingwaves[J]. Review of Progress in Quantitative Nondestructive Evaluation, 2011, 1335(1): 322-329. [7]SOHNH,LIMHJ,DESIMIOMP, et al..Nonlinearultrasonicwavemodulationforonlinefatiguecrackdetection[J]. Journal of Sound and Vibration, 2014, 333(5):1473-1484. [8]CONNOLLYGD,ROKLINSI.Quantitativeenhancementoffatiguecrackmonitoringbyimagingsurfaceacousticwavereflectioninaspace-cycledomain[C]. AIP Conference Proceedings, 2011:1499-1506. [9]刘斌, 刚铁, 万楚豪,等. 复杂结构焊缝的非线性超声检测方法[J].焊接学报, 2015, 36(3):39-43. LIUB,GANGT,WANGCH, et al..Nonlinearultrasonicmethodfordetectingweldofcomplicatedstructure[J]. Transactions of the China Welding Institution, 2015, 36(3):39-43.(inChinese) [10]罗玉昆, 罗诗途, 罗飞路,等. 激光超声信号去噪的经验模态分解实现及改进[J]. 光学 精密工程,2013, 21(2):479-487. LUOYK,LUOSHT,LUOFL, et al..Realizationandimprovementoflaserultrasonicsignaldenoisingbasedonempiricalmodedecomposition[J]. Opt. Precision Eng., 2013, 21(2):479-487.(inChinese) [11]RAZIP,TAHERIF.A.Vibration-basedstrategyforhealthmonitoringofoffshorepipelinesgirth-welds[J]. Sensors, 2014, 14(9):17174-17191. [12]HONGXB,WANGH,WANGT, et al..Dynamiccooperativeidentificationbasedonsynergeticsforpipestructuralhealthmonitoringwithpiezoceramictransducers[J]. Smart Materials & Structures, 2013, 22(4): 3-15. [13]芦吉云, 王帮峰, 梁大开. 基于小波包特征提取及支持向量回归机的光纤布拉格光栅冲击定位系统[J]. 光学 精密工程, 2012, 20(4):712-718. LUJY,WANGBF,LIANGDK.IdentificationofimpactlocationbusingFBGbasedonwaveletpacketfeatureextractionandSVR[J]. Opt. Precision Eng.,2012, 20(4):712-718.(inChinese) [14]MOSTAFAPOURA,DAVOODIS.Atheoreticalandexperimentalstudyonacousticsignalscausedbyleakageinburiedgas-filledpipe[J]. Applied Acoustics, 2015, 87:1-8. 洪晓斌(1979-),男,广东揭阳人,教授,博士生导师,2002年于武汉理工大学获得学士学位,2007年于华南理工大学获得博士学位,主要从事无损检测技术与装备、网络化测控技术及仪器等方面的研究。E-mail:mexbhong@scut.edu.cn 刘桂雄(1968-),男,广东揭阳人,教授,博士生导师,1990年于重庆大学获得学士学位,1995年于重庆大学获得博士学位,主要从事新型智能传感技术、网络化测控技术、制造过程质量检测、建模及控制等方面的研究。E-mail:megxliu@scut.edu.cn (版权所有未经许可不得转载) Damage detection of nonmetallic pipe by using nonlinear ultrasonic guided wave with signal delay HONG Xiao-bin, FENG Jin-heng, LIN Pei-song, LIU Gui-xiong* (School of Mechanical & Automotive Engineering,South China University of Technology, Guangzhou 510641, China) *Corresponding author, E-mail:megxliuscut.edu.cn Asthedamagesonnonmetallicpipes,especiallyearlydamages,aredifficulttobedetectedbyultrasonicguidedwave,thispaperproposesanonlinearultrasonicguidedwavewithsignaldelaytodetectandlocalizethedefectsonnonmetallicpipes.Basedonthenonlinearultrasonicwavetheory,thedamagestatesofnonmetallicpipeswereanalyzedandanincentivemethodwithmixedsignalsfromthesameendofthesignaldelaywasdevelopedtogeneratesignaldelayaccordingtodifferentspeedsofthemixingsignalsandtoimplementnonlinearmodulation.TheinstantaneouscharacteristicsofdelaysignalwereextractedbyHHT(Hilbert-HuangTransformation),anddamagelocationwasachievedbyanalyzingdifferentnonlinearmodulationgroupswithsignaldelay.PVC(Polyvinylchloride)pipeswereusedforexperiments.Inintactcondition,thestandardizedreferencevaluesofsignaldelaygroupsis0.518 8.Indamageofonecrack,standardizedvalueofsignaldelaygroupsis0.593 7andtherelativeerroris3.277%.Moreover,indamageoftwocracks,thestandardizedvalueofsignaldelaygroupsare0.593 7and0.607 3,andtheabsoluteerrorislessthan4mm.Comparedtothewaveletenvelopelocationapproach,therelativeerrorwithonecrackrisesto36.4%.Theseresultsturnoutthattheapproachproposedinthispaperiseffectiveandaccurateforthedamagedetectionandlocationofnonmetallicpipes,andisavailableforthemulti-damagedpipes. nonmetallicpipe;damagelocation;ultrasonicguidewavedetectionwithdelaysignal;nonlinearmodulation 2016-03-20; 2016-04-15. 国家自然科学基金资助项目(No.51305141);广东省自然科学基金资助项目(No.2014A030313248);广州市科技计划项目(No.201607010171) 1004-924X(2016)07-1685-09 TB553 Adoi:10.3788/OPE.20162407.1685


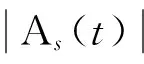









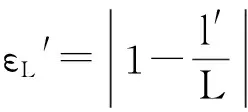

5 结 论



