基于Mindlin公式的群桩基础柔度矩阵

程 永 巍

(张家口市华瑞房地产开发有限责任公司,河北 张家口 075000)



基于Mindlin公式的群桩基础柔度矩阵

程 永 巍

(张家口市华瑞房地产开发有限责任公司,河北 张家口 075000)

首先简要介绍了桩基沉降的分析方法和我国规范相关规定，重点讲解了基于弹性理论Mindlin解的Geddes公式计算法.利用Mindlin公式对单桩情况进行了沉降计算，得到了一些结论，在单桩的基础上利用Mindlin解对3×3群桩基础过行了柔度矩阵的求解.利用有限元软件ANSYS模拟了长径比对沉降的影响，引出有关Mindlin解应用于沉降计算时存在的一些不足点.

单桩;群桩;沉降;ANSYS;Mindlin解;分层总和法;柔度矩阵

0　引　言

随着我国建设规模的扩大，桩基础领域发展迅速，桩基础在减少建筑物沉降，提高地基承载力方面具有独特的优点和不可替代的作用.尽管桩基础与天然地基上的浅基础比较，沉降量可大为减少，但随着高层、超高层建筑物的增多，使得基底荷载越来越大，对基桩承载力和变形提出了更高的要求，在很多情况下，桩基础也需要进行沉降计算.

本文首先简要介绍了桩基沉降的分析方法和我国规范相关规定，重点讲解了基于弹性理论Mindlin解的Geddes公式计算法.利用Mindlin公式对单桩情况进行了沉降计算，得到了一些结论.在单桩的基础上利用Mindlin解对3×3群桩基础过行了柔度矩阵的求解.利用有限元软件ANSYS模拟了长径比对沉降的影响.最后总结了有关Mindlin解应用于沉降计算时存在的一些问题.

1　沉降分析方法

1.1单桩的沉降分析方法

目前单桩沉降计算方法主要有下述几种：荷载传递分析法;弹性理论法；剪切变形传递法；有限单元分析法；边界元法；混合法；经验法及其他简化方法.

其中，荷载传递分析法的关键在于求解传递函数，研究人员提出了多种形式的传递函数；剪切变形传递法假定当荷载水平p/pu较小时，桩在轴向荷载作用下沉降较小，桩土之间不产生相对位移，亦即桩沉降时周围土体亦随之产生剪切变形，剪应力从桩侧表面沿径向四周扩散到周围土体中，摩擦桩一般在工作荷载作用时,桩端承担的荷载比例较小，沉降主要是由桩侧传递的荷载所引起；弹性理论法是对桩土系统用弹性理论方法来研究单桩在竖向荷载作用下桩土之间的作用力与位移之间的关系，进而得到桩对土、土对桩、桩对桩以及土对土的共同作用模式.

群桩沉降计算方法主要有：等代墩基法；基于弹性理论Mindlin解的Geddes公式计算法；相互作用因子叠加法；沉降比法；有限单元法；边界元法；混合法等.

1.2群桩的沉降分析方法

1.2.1实体深基础(等代墩基)法

实体深基础法是现在工程界应用最广泛的一种计算群桩沉降的方法.该计算模式是将在桩端以上的一定范围的承台、桩及桩周土当成实体深基础,在此等代墩基范围内,不计从地面到桩端平面间的压缩变形,然后按照扩展基础的沉降计算方法来计算群桩的沉降.适用于桩距不超过6d的群桩基础.1.2.2弹性理论法

弹性理论法群桩沉降分析的基本假定与单桩相同,其主要依据是Mindlin解的位移与应力解,以此为基础形成位移法和应力法,此外还发展了一种简化弹性理论位移法.

1.2.3我国规范相关规定

在计算建筑物的沉降时,国内一般运用Mindlin公式或者Boussinesq解来计算附加应力.《建筑地基基础设计规范》(GB50007-2002)和上海市标准《地基基础设计规范》(DGJ08-11-1999)中也是采用Mindlin解来确定桩基础荷载作用下地基土中的附加应力,最后采用分层总和法计算最终的沉降量.

2　基于Mindlin公式的群桩沉降计算

明德林解是当荷载作用于半无限弹性体内部时求弹性体内部应力场的解答.如图1，半无限弹性体表面坐标原点O下c深度点上作用有竖向力Q时，在弹性体内任意点M(x,y,z)处，引起的竖向应力，按明德林解，可表示为：

(1)

式中,Ip称为应力影响系数.

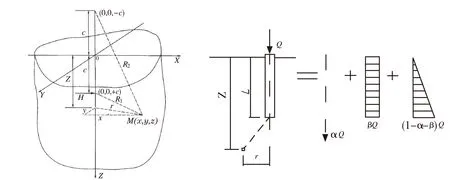
图1地基附加应力计算示意图图2明德林-盖得斯单桩荷载的分解

盖得斯根据桩的传递荷载特点，将作用于单桩顶上的总荷载Q分解为桩端阻力Qp和桩侧阻力Qs，而桩侧阻力Qs又可分为均匀分布的总摩阻力Qs1和随深度线性增加的总摩阻力Qs2所组成，如图2所示.

Qp=αQ,Qs1=βQ,Qs2=(1-α-β)Q

(2)

其中,α为端阻力占总荷载的比例，β为均布摩阻力占总荷载的比例.系数α，β应根据当地工程的实测资料统计确定.对于一般摩擦桩可假设桩侧阻力全部是沿桩身线性增长，即β=0.

盖得斯又根据明德林解，推导出,和在地基土中产生的附加应力计算公式.应用这些公式就能计算各类桩在地基中产生的附加应力，进而计算出桩基的沉降.这种方法称为明德林-盖得斯法，简称明德林法.

这样每根摩擦桩在地基中某点的竖向附加应力为该桩的桩端荷载及桩侧荷载产生的竖向附加应力和之和.对于有m根桩的情况，再将每根桩在该点所产生的附加应力逐根叠加，按下式计算：

(3)

式中,Pi为第i层土中点处产生的附加应力.

σzp、k为第k根桩的桩端荷载在第i层中点处产生的附加应力：

(4)

如果假设β=0，则第k根桩的桩侧荷载在该点产生的竖向附加应力：

(5)

IP为桩底集中力的应力影响系数，经积分得出：

(6)

Is2为桩侧分布荷载沿桩身线性增长时的应力影响系数，经积分得出：

(7)

其中,A2=n2+(m-1)2;B2=n2+(m-1)2;F2=n2+m2;n=r/l;m=z/l

然后，仍然按单向压缩的分层总和法计算沉降.

(8)

式中,s为桩基最终沉降量,mm；n计算分层数；Esi第i层土在自重应力至自重应力加上附加应力作用段的压缩模量,MPa;pi桩端平面下第i分层土的竖向附加应力平均值;ΨP桩基沉降计算经验系数.

3　压缩层厚度确定方法

现行规范中确定压缩层厚度的方法主要由基础宽度比法、应力比法及变形比法3种.

3.1基础宽度比法

《建筑地基基础设计规范》中给出当无相邻荷载影响、基础宽度b在1-30 m范围内时，基础中点地基变形计算深度Zn的简化计算公式:

(9)

式中,δSi′为在计算深度范围内,第i层土的计算变形值;δSni′为计算层深度范围内总的变形值;δSn′为在由计算深度向上取厚度为δz的土层计算变形值，δz根据基础宽度确定.

基础宽度法十分简单，易于确定，并且总结了相关经验数据，应该算是一种经验的估计，使用很方便，在本次计算中将采用基础宽度法.应力比法沿用至今具有相当的经验，确定计算深度相对简单，但它没有考虑到土层的构造与性质，过于强调荷载对压缩层深度的影响，同时由于桩长的增加导致桩端位置处的土体自重应力值很大，即桩端平面处附加应力的计算值要小于自重应力值的20%，有时甚至要小于自重应力值的10%，这种情况下算不出桩端下的压缩沉降，这显然是不合理的;而变形比法直接考虑了桩端以下土体随深度增加，压缩变形量的变化对桩基最终沉降量的影响，但由于没有考虑荷载对压缩层厚的影响，计算厚度需要对沉降量的计算才能确定，同时该方法另一缺陷是压缩层厚度的确定与桩端位置平面处的附加应力无关，即如果地层条件确定，无论上部荷载多大压缩层厚度是不变的，这显然不合理.

4　基于Mindlin公式的群桩基础的柔度矩阵求解

4.1单桩试算

4.1.1基本工况

如图3所示，取单层土，土层厚度h=20 m，桩径d=500 mm，桩长l=15 m，土的压缩模量Es=0.4 Mpa,土的泊松比u=0.3，桩基沉降计算经验系数Ψp=0.5端阻力占总荷载的比例α=0.15，桩侧阻力占总荷载的比例β=0，桩顶的竖向载荷Q=1 N，计算点深度Z=25 m.

4.1.2附加应力的计算

M点的竖向附加应力为该桩的桩端荷载Qp及桩侧荷载Qs产生的竖向附加应力σzp和σzs之和.

P=σzp+σzs

(10)

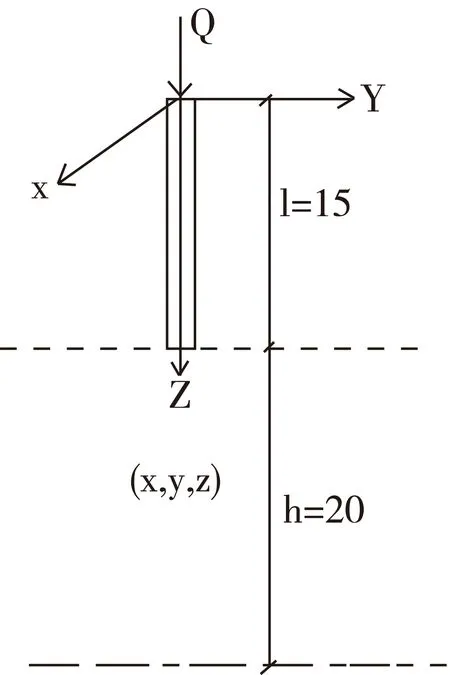
图3　单桩沉降计算示意图

(1)桩端荷载在M点处产生的附加应力可得：

其中，

F2=n2+m2=1.6672,A2=n2+(m-1)2=0.444,

B2=n2+(m+1)2=7.111

代入已知条件得：

Ip=0.49(C程序结果：Ip=0.492735)

(2)桩侧荷载在M点处产生的附加应力：

同理代入已知条件得：

Is2=0.298(C程序结果：Ip=0.297816)

P=σzp+σzs=13.212×10-4N/m2

4.1.3压缩沉降

附加应力p得到后后，按单向压缩的分层总和法计算沉降，此算例中只考虑了一层土.

4.1.4考虑分层厚度的变化

为探讨分层厚度对沉降量的影响，在20 m的土层厚度范围内考虑分层，分层厚度分别采用10 m，4 m，2 m，即考虑分为2层、4层、和10层这三种情况，见表1.利用Mindlin公式按照上述沉降计算的步骤可求各沉降量.

表1　不同分层厚度沉降计算

4.1.5小结

(1)Geddes应力公式是将桩端压应力简化为作用于桩端的集中力，将桩侧剪应力简化为沿桩身轴线分布的集中力，据此求得桩端平面以下任一点的竖向应力系数.在计算过程中没有体现桩径d的影响，但实际情况中显然桩径对沉降是有影响的.

(2)由于桩轴线处(x=0,y=0)会引起n=0，在计算桩侧分布荷载沿桩身线性增长时的应力影响系数Is2时，n出现在分母上，利用公式计算会出现奇异点，为避免这一现象，本算例中取x=0.25，y=0处的应力作为轴线上的应力.

(3)手算桩底集中力的应力影响系数和桩侧分布荷载沿桩身线性增长时的应力影响系数的过程简单但繁琐，所以在手算的基础上利用C语言编写了计算应力影响系数的程序.将C程序计算结果对比手算结果对比，结果一致，说明程序编写的正确性.因此，在之后的算例中，为避免重复简单而又繁琐的计算劳动量，都采用C程序来计算应力影响系数.

(4)用Mindlin公式计算桩基沉降时，规范都推荐使用分层总和法,但对土层计算分层厚度的划分,规范并没有给出明确的规定.本次计算中取了三个不同的分层厚度得到了三个沉降量.

4.23×3群桩柔度矩阵求解算例

4.2.1基本工况

如图4所示，3×3群桩桩的间距Sa=2 m，其他条件同单桩情况.

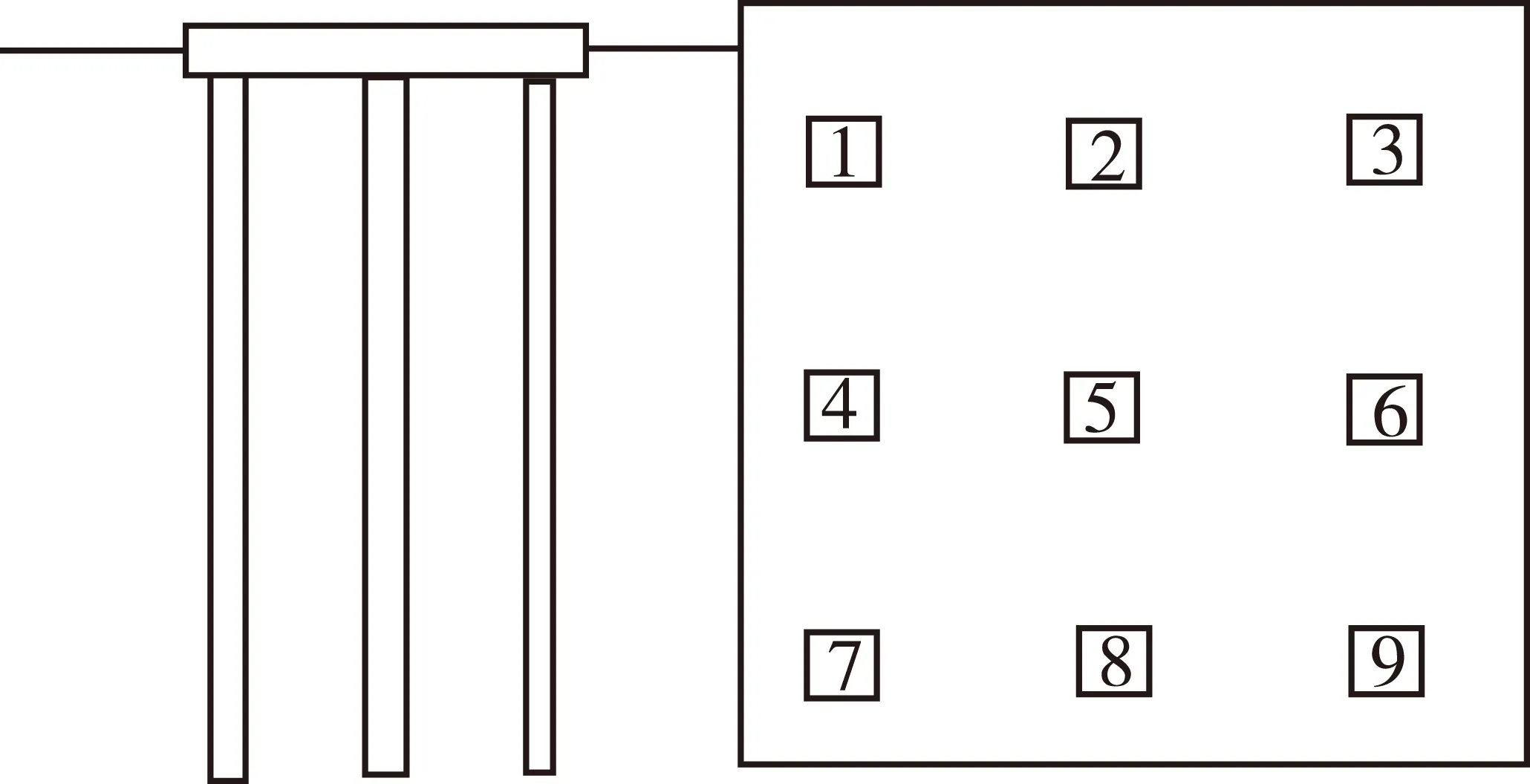
图4　群桩沉降计算示意图

4.2.2柔度矩阵的求解

柔度矩阵中表示作用于j点的单位力在i点引起的位移.

对于3×3群桩基础，其柔度矩阵为9×9，如下：

桩之间的相互作用体现在其相对位置的不同，对于3×3群桩基础相对坐标存在六种情况.

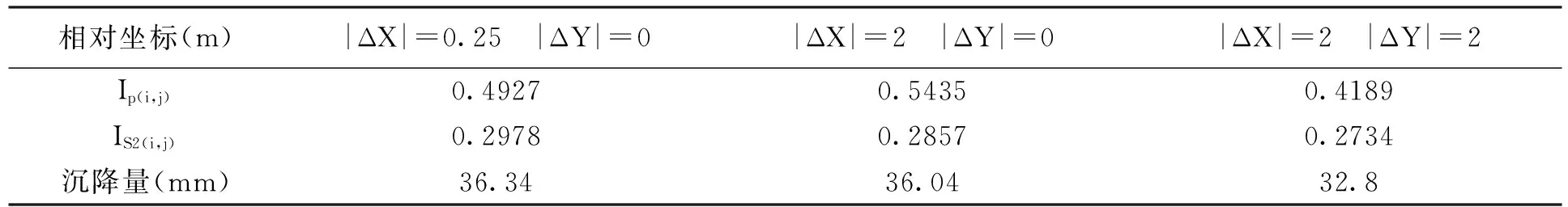
表2　群桩沉降计算

续表：

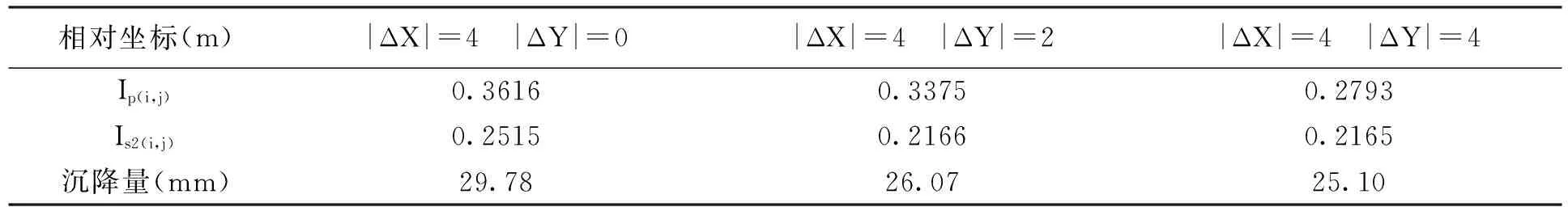
相对坐标(m)|ΔX|=4 |ΔY|=0|ΔX|=4 |ΔY|=2|ΔX|=4 |ΔY|=4Ip(i,j)0.36160.33750.2793Is2(i,j)0.25150.21660.2165沉降量(mm)29.7826.0725.10

得柔度矩阵为：

4.2.3群桩的沉降计算

群桩的沉降计算时，可充分利用其对称性.

(1)1号桩，3号桩，7号桩，9号桩

(2)2号桩，4号桩，6号桩，8号桩

∑P=11.68×10-3

(3)5号桩

∑P=12.47×10-3

5　单桩的有限元模拟

单桩是群桩分析的基础，可利用ANSYS对单桩中的附加应力分布进行研究.在手算的基础上，通过有限元模拟不同L/d时桩轴心处桩端下地基土中的沉降.

5.1模型参数

在均匀单一土层中，参数的选取与前一节中单桩试算中基本一致.

桩为线弹性材料：桩长l=15 m，桩的弹性模量E=25 Mpa,桩的泊松比为0.2，密度为2500 Kg/m3，桩的长径比L/d是变化的；土体为D-P模型材料：土的压缩模量Es=0.4 Mpa,土的泊松比u=0.3，密度为2000 Kg/m3，粘聚力c=19,摩擦角为32度，膨胀角为30度.

理论上，地基在半空间上是无限延伸的，用有限元来模拟具有一定的局限性.但是，实际上地基中的应力影响范围总是有限的，而且只要边界取得较大，单元划分得较为合理，用有限元近似分析的精度是可以接受的.桩身左右取10倍桩径(5 m)及桩端以下土体分别取20倍桩径(10 m).

5.2单元的选取

桩身和土体都采用六面体8节点单元solid45实体单元，每个节点具有X、Y、Z三个方向的自由度.具有塑性、膨胀、流变、应力强化、大变形和大应变的能力.

接触问题一般分为两类：刚体-柔体的接触、半柔体-柔体的接触.ANSYS支持3种接触方式：点-点、点-面、面-面.本次模拟采用的是刚体-柔体、面-面的接触.刚性面被当作目标面，分别用Target169和Target170来模拟2-D和3-D的目标面，柔性体的表面被当作接触面，用Contact171、Contact172、Contact173和Contact174来模拟.

5.3边界条件

位移边界条件：对土体左右两侧边界分别约束其水平位移,对土体底部边界同时施加水平和竖向约束.

接触条件：由于桩相对于土来说，弹性模量大得多，所以桩上的面为刚性目标面选用Target170，目标面对应的土体表面为接触面选用Contact173.

力边界条件：桩顶作用1N集中力.

5.4单桩沉降分析

桩的直径取500 mm时，长径比L/d=30.图5给出了单桩有限元分析时的网格划分示意图；图6给出了桩与桩周土及桩底与土接触时设置的接触面；图7给出了Z方向位移云图.

图5单桩及桩土有限元模型图6桩与土的接触面设置

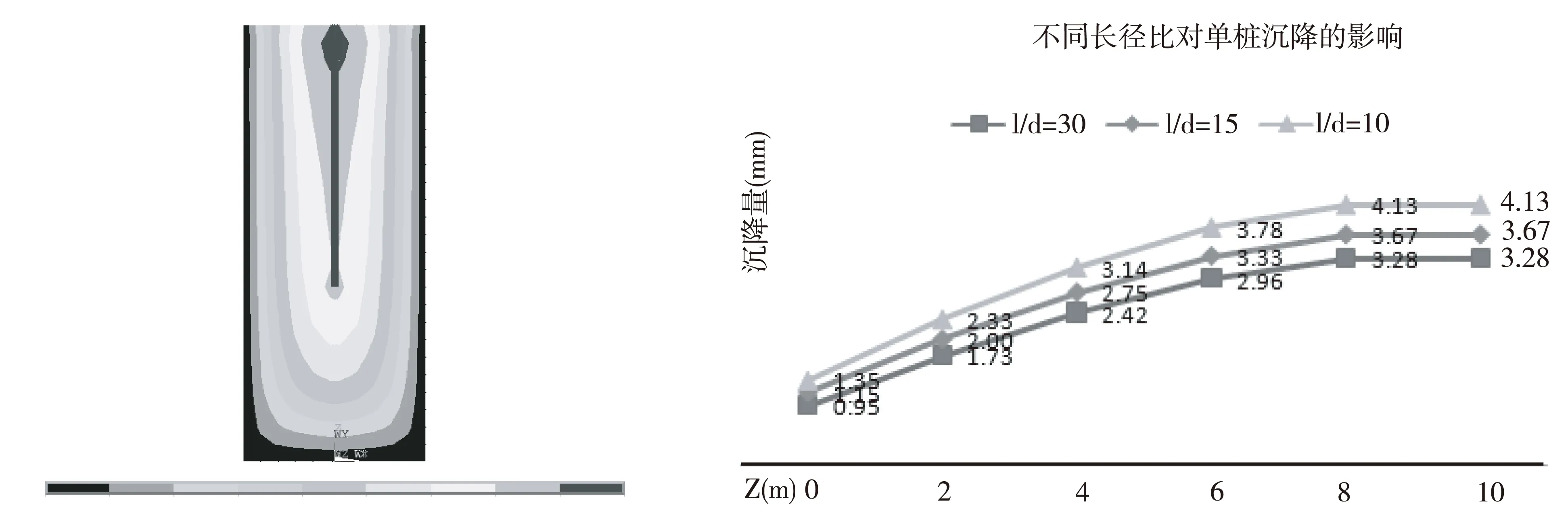
图7Z方向位移云图图8不同L/d时单桩的沉降

变化长径比L/d，使其取比值为30，15，10三种情况，取桩端下2 m、4 m、6 m、8 m、10 m处的位移作比较，如图8的所示.

可以看出，沿着深度方向沉降衰减很快，随着L/d的减小桩端下同一深度处的沉降量随之增大.因此，桩的长径比L/d是影响群桩基础受力特性的又一重要因素，但mindlin解中无法体现d的影响.

6　结　论

本文通过基于Mindlin解的单桩沉降计算和群桩沉降计算，可以得到有关Mindlin解应用于沉降计算时存在的一些问题.

(1)Geddes应力公式是将桩端压应力简化为作用于桩端的集中力，将桩侧剪应力简化为沿桩身轴线分布的集中力，据此求得桩端平面以下任一点的竖向应力.计算结果会在桩端附近产生较大的应力集中现象,导致桩端计算厚度范围内应力大大超过土的强度,使计算失真,沉降偏大.

(2)由于桩轴线处(n=0)，竖向应力按Mindlin公式计算应力影响系数时会出现奇异点.

(3)Geddes应力叠加分层总和法对于大桩群手算很繁琐，可采用数值方法计算.本文采用C语言编制了计算应力影响系数的程序.

(4)用Mindlin公式计算桩基沉降时，规范都推荐使用分层总和法，但对土层计算分层厚度的划分，规范并没有给出明确的规定.从理论上来说，土层厚度划得越细，结果应该越精确，但计算机时就将增大，如果划得粗,沉降值就会变小，这样，不同的计算分层厚度会对最终沉降产生影响.本次计算中取了三个不同的分层厚度得到了三个沉降量.

(5)Mindlin计算过程中没有体现桩径d的影响，也未考虑桩身的弹性压缩.利用有限元软件模拟单桩沉降时，对于不同长径比L/d，桩端以下沉降不同.这说明桩的长径比L/d是影响群桩基础受力特性的又一重要因素，但mindlin解中无法体现d的影响.

(6)Mindiin方法计算桩基应力的合理性被越来越多的学者所接受并采用，该法有一个突出特点，就是不同桩距、不规则布桩、端阻比、侧阻分布模式、桩长度不一等因素均可在计算中如实反映，而Boussinesq应力计算方法则无法考虑这些因素.

[1]秋仁东.竖向荷载下桩身压缩和桩基沉降变形研究[博士学位论文].中国建筑科学研究院,2011

[2]徐志英.以明特林(Mindlin)公式为根据的地基中垂直应力的计算公式[J].土木工程学报,1957,4(4):485～497

[3]吴家龙.弹性力学[M].上海:同济大学出版社,1996

[4]周景星,李广信,虞石民,王洪瑾.基础工程[M].北京:清华大学出版社,2007

[5]建筑桩基技术规范(JGJ94-2008).北京:中国建筑工业出版社,2008

[6]建筑地基基础设计规范(GB50007-2011).北京:中国建筑工业出版社，2012

[7]地基基础设计规范(DGJ08-11-1999).上海:上海市工程建设标准化办公室,1999

[8]桩基工程手册.北京.中国建筑工业出版社,1995

[9]ANSYS土木工程应用实例.中国水利水电出版社,2010

Flexibility Matrix of Group Piles Foundation based on Mindlin Solution

CHENG Yong-wei

(Zhangjiakou Huarui Real Estate Development Co.,Ltd，Zhangjiakou 075000,China)

Firstly,this paper briefly introduces the analyzing methods for pile settlement and some relevant provisions in our standard,and mainly explains Geddes formula based on Mindlin solution of elastic theory as well.Using Mindlin formula, we carried out the settlement calculated for single pile and got some conclusions.On the basis of single pile,the flexibility matrix for a 3×3 group piles foundation is solved.Then,finite element software ANSYS is used to simulate the effect of aspect ratio on the deposition.Finally,combining all the results,we summarized some shortcomings of the Mindlin solution used in settlement calculations.

single pile;group piles foundation;settlement;ANSYS;Mindlin solution;layerwise summation method;flexibility matrix

2015-11-20

程永巍(1987-)，男，助理工程师，主要从事项目前期手续办理工作.

TU 4

A