三维复杂群桩水流力特性数值模拟研究

闫杰超，徐 华

（1.中铁大桥勘测设计院集团有限公司，湖北 武汉 430050；2.南京水利科学研究院，江苏南京 210029）

引 言

群桩作为主要的桥梁或码头基础形式之一，具有减小对水流的影响及河床冲刷的特点[1]。但不同的群桩布置形式常引起水流的复杂分配，造成其水流力的计算困难，极大的影响桥梁或码头设计工作者对其基础的设计工作。

群桩的水流力或水流力系数的研究是一个传统的科学问题。唐士芳[2]通过模型试验研究了方形、圆形、棱形、工字形、长板型墩柱阻力系数与水深桩径比的关系；J.C.Heideman[3]探讨了单圆柱、5×5矩形柱和正方形圆柱柱群、单矩形棱柱以及单正方形棱柱的水流阻力系数；邓绍云[4]通过物理试验研究了双桩在横排与列排条件下的遮掩影响与横向干扰影响；翁松干等[5]研究高桩码头群桩的纵向遮掩及横向干扰影响；Zdravkovich[6]通过研究串联双圆桩流场认为桩体之间的相互影响主要通过其产生的漩涡脱落变化造成的；并且邓绍云[7]研究群桩的流态影响认为垂直于水流方向排列桩柱密度，对桩群绕流的影响甚于顺水流方向桩柱的排列的密度；Hoerner[8]研究了双柱前后布置时不同桩距的水流力系数变化规律，并且也认为前后桩水流力的不同变化是其产生的漩涡脱落变化造成的；邓绍云[9]通过双圆柱横向及列向不同桩距下的水流力系数进行研究得到了相应的群桩水流力计算公式；吕启兵[10]认为邓绍云提出的桩群总阻力计算的方法与公式存在一定的局限性。从上述研究可以看出，目前关于群桩水流力或相互影响研究多以一排多桩、一列多桩或双柱设定下在不同间距下的研究，而并未以实际群桩形式进行系统的研究。同时，相关研究并未结合工程实际对于外包络线不是矩型的群桩进行研究，如菱型、圆型及哑铃型等实际工程中已使用的桥墩基础结构。

基于上述研究现状，通过建立三维水动力模型研究了群桩在不同桩距下的横向、纵向及总力分布规律。并对不同群桩型式的横向、纵向及总力分布规律进行了研究，以回答目前群桩总水流力计算中出现的问题及为实际工程提供一定的技术指导。

1 模型建立及验证

1.1 模型建立

数学模型采用ANSYS Fluent建立，水槽长度5.2～8.0 m，宽度2.4～3.0 m，群桩置于水槽前半部分。所研究的群桩为m列×n排，桩的类型为圆桩。其中，横向桩距SH均等于纵向桩距SZ，并定义群桩外包络线为群桩形状。如图1所示。模型湍流封闭方程采用比较成熟的RNGk-ε。

图1 群桩模型示意

1.2 网格无关性验证

首先对所建立三维水动力模型进行网格无关性验证。其中，群桩为4列×6排，桩间距SH=SZ=3D，桩径D=2.0 cm。模拟条件为V=0.185 m/s，h=0.225 m。模型群桩为4列×6排，桩间距SH=SZ=3D，桩径D=2.0 cm。模拟条件为V=0.185 m/s，h=0.225 m。由表1可知，对所建立数学模型分别采用2.0 cm、1.5 cm及1.0 cm的全局网格尺寸，其群桩中各桩局部网格均采用6层边界层网格，且第一层网格厚度满足为桩径D的1/20，其网格数分别约为53万、81万及268万个。从模拟结果来看，随着网格尺寸的减小，其水流总力的误差也逐渐减小。当网格尺寸为1.0 cm时，模拟结果与实际测量结果相差约13%。为减少模拟时间及代价，研究认为1.0 cm的网格尺寸基本满足研究的需要。

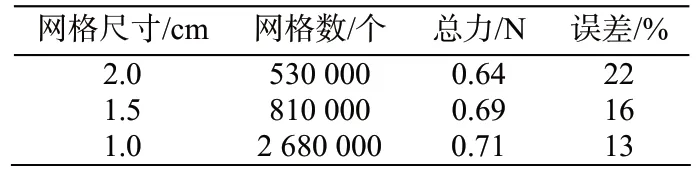
表1 网格无关系验证

1.3 群桩阻力验证

为验证所建立数值模型的正确性，本文采用文献[11]中物理模型试验值进行对比验证。模拟对比结果如表2，采用1.0 cm的全局网格尺寸模拟出的群桩总水流力误差在10%左右，模拟值和试验值基本近似，说明本数学模型科学可靠，可用于开展相关群桩水流力特性研究工作。

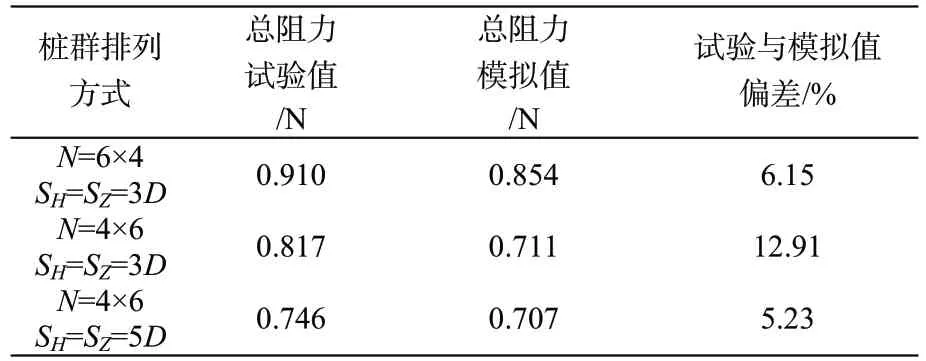
表2 桩群总阻力试验值与模拟值验证

2 矩型群桩模拟结果与分析

2.1 不同桩距的群桩纵向水流力分布特性

以研究矩型群桩在不同桩距下的纵向水流力分布规律，本文以4列×6排及桩间距SH=SZ的群桩为例，在5D、6D、7D、8D、9D及10D桩距下分析群桩中纵向水流力的分布规律。其中，单桩桩径D=2.0 cm，单桩水流力为0.68 N。模拟条件为V=0.185 m/s，h=0.225 m。

如图2，矩型群桩水流力纵向分布呈前排桩向后排依次减小的规律，且首排桩水流力稍微大于单桩水流力值，这与先前研究规律基本一致。从第三排桩之后，其水流力大致相同或减小较小；当随着桩距增大，首排桩水流力及最尾排桩水流力变化较小或基本不变，中间排桩变化稍大。其说明随着桩距的变化，后排桩群对首排桩的影响较小，且前排桩群对最尾排桩的遮掩效应具有一定的延后性。

图2 不同桩距矩型群桩的纵向水流力分布规律

2.2 不同桩距的群桩横向水流力分布特性

以研究矩型群桩在不同桩距下的横向水流力分布规律，本文仍以4列×6排及桩间距SH=SZ的群桩为例，在5D、10D及15D为例分析不同桩距的群桩横向水流力分布特性。其中，单桩桩径D=2.0 cm，单桩水流力为0.68 N。模拟条件为V=0.185 m/s，h=0.225 m。

如图3所示，矩型群桩水流力横向分布基本呈两边大，中间小的对称分布规律，这与先前研究规律基本一致。首排桩的横向水流力对称性分布并不明显，后排桩的分布较为明显。随着桩距的增大，其后排桩这种“两头大，中间小”的分布规律趋于均匀化，但最尾排桩仍有一定的延后性。说明随着桩距的增加，群桩引起的两侧水流加速减小，其两侧桩的水流力与中间桩水流力相对均一化。

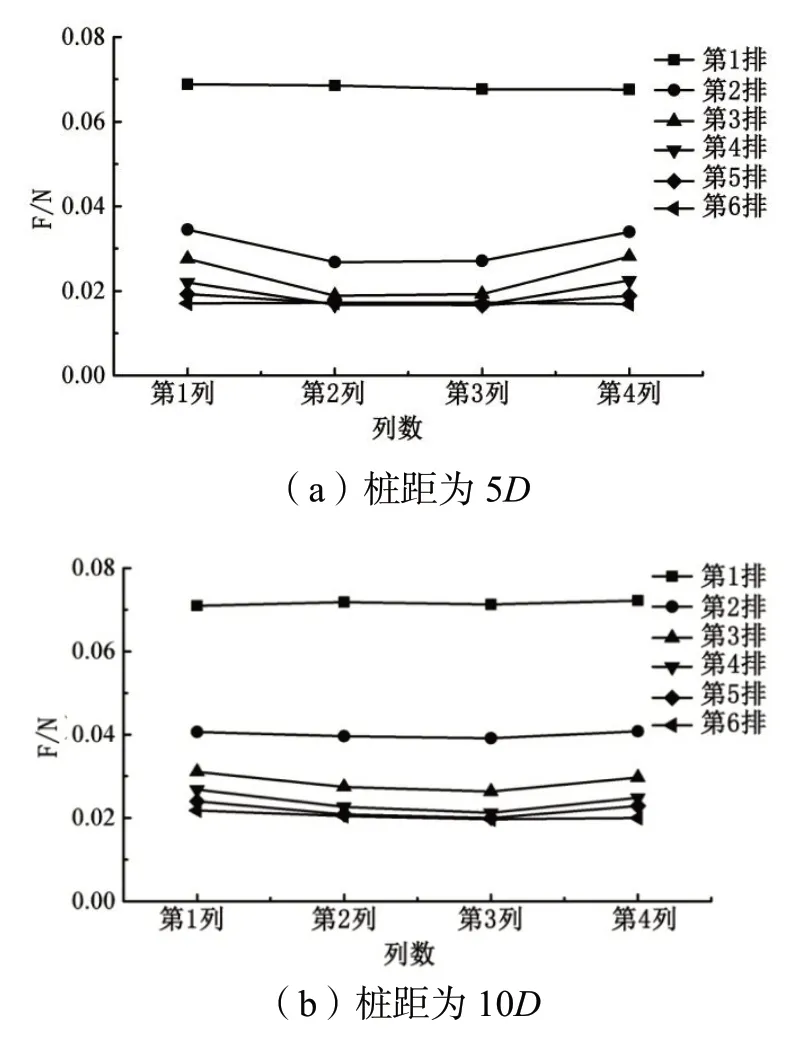
图3 不同桩距时横向水流力分布规律

2.3 不同桩间距对群桩总阻力的影响

进而本文研究了矩型群桩总水流力随着桩距变化的响应规律，其群桩类型及水流条件与上述一致。由图4可知，随着桩距的增加，矩型群桩水流总力呈先增加后减小，再增大的变化规律。从实测数据点也可得出在桩距5D时的水流总力小于桩距3D时。同时，采用邓绍云[9]提出群桩水流总力计算公式计算发现，其理论公式计算而得的矩型群桩水流总力也呈先增大后减小，再在增大的变化规律。但理论公式计算认为当桩距为2D时，该群桩水流总力为0，且随着桩距的增大，其理论值与模拟值差值逐渐增大。本文研究认为其研究成果是基于双柱在串或并联条件下得出的纵向遮掩或横向干扰影响系数，继而拟合得到的计算公式，其与实际群桩在桩距变化下的规律并不一致。同时，本文研究认为群桩在第三排桩以后可近似认为相等，且横向桩的水流力呈“两头大，中间小”的规律，建议矩型群桩水流力计算公式应采用纵向至少三排桩，横向至少三排桩的排列布置来研究，而非双桩。

图4 矩型群桩水流总力随桩距变化关系

3 异型群桩模拟结果分析

3.1 不同桩间距对群桩总阻力的影响

桥梁或码头工程中，其群桩并非都是矩型的，也存在菱型群桩、圆形群桩及哑铃型群桩。如苏通大桥及南京四桥采用了哑铃型群桩型式，铜陵大桥采用了圆型群桩型式等。

对于异型群桩水流力，研究在实际工程中常采用的2D、3D、4D及5D桩距下的水流总力变化规律。其中，桩径D=2.0 cm，模拟条件为V=0.185 m/s，h=0.225 m。如图5，随着桩距的增加，菱型群桩水流总力呈增加的趋势，而圆型及哑铃型群桩水流总力呈先增大后减小的趋势。从受水流总力影响出发，建议实际工程中采用2D桩距进行异型群桩的基础设计。

图5 异型群桩水流总力随桩距变化关系

3.2 不同桩距的群桩纵向水流力分布规律

对于异型群桩的纵向水流力分布。如图6所示，菱型群桩纵向水流力呈先减小后增大，再减小的变化规律。增大位置在后排群桩宽度减小处，可能水流在该处加速，导致两侧桩水流力增大。同时，随着桩距的增大，纵向各桩水流力也相应呈增大趋势；圆型群桩纵向水流力呈减小的趋势，从第三排桩后，纵向各桩水流力基本相等。同时，随着桩距的增加，第三排后的各桩水流力变化较小；哑铃型群桩纵向水流力也呈先减小后增大，再减小的分布规律。增大位置是在哑铃增宽处，此排两侧桩水流力受上游桩遮掩较小，受水流力较大。同时，随着桩距的增加，纵向各桩水流力也相应增加。

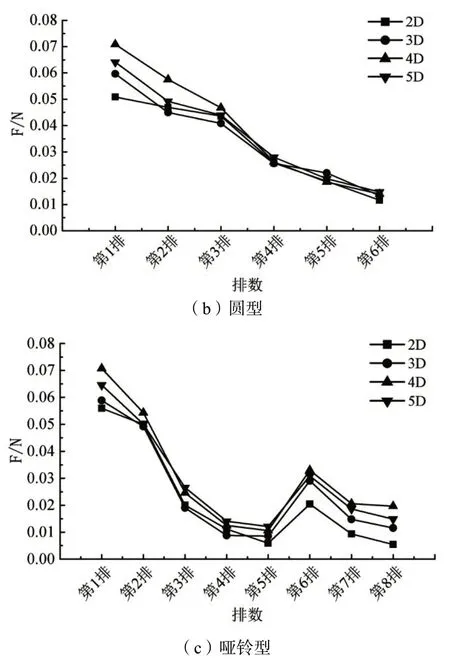
图6 不同桩距异型群桩的纵向水流力变化规律

3.3 不同桩距的群桩横向干扰系数影响

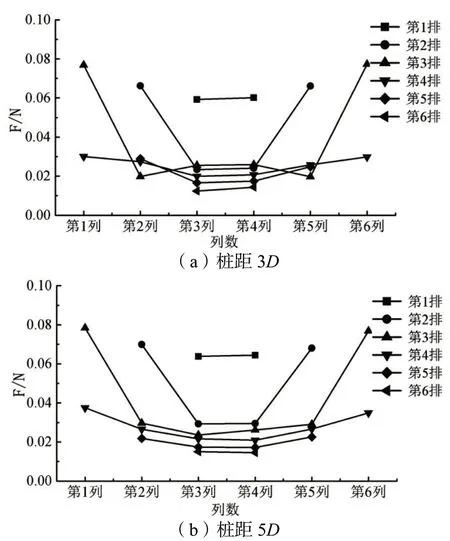
图7 不同桩距圆型群桩的横向水流力分布特性

图8 不同桩距哑铃型群桩的横向水流力分布特性

以圆型群桩与哑铃型群桩为例，分析其在3D和5D间距下的横向水流力分布规律。如图7与图8所示，圆型群桩的横向水流力也呈“两边大，中间小”的分布规律，且随着桩距的增大，其横向水流力分布有均匀化的趋势。同理，哑铃型群桩的横向水流力也呈“两边大，中间小”的分布规律，且随着桩距的增大，其横向水流力分布有均匀化的趋势。说明桩距的增大减小了群桩与水流的相互影响。

4 结 语

本文通过建立三维水动力数学模型研究了不同型式群桩在不同桩距下的水流力分布特性，并结合水动力学理论分析了其出现不同分布规律的本质机理，为相关的研究提供一定的指导，也可为实际桥梁或码头工程的基础设计提供一定借鉴。

1）通过研究发现，矩型群桩在第三排桩之后，其水流力大致相同或减小较小；当随着桩距增大，首排桩水流力及最尾排桩水流力变化较小或基本不变，中间排桩变化稍大。其说明随着桩距的变化，后排桩群对首排桩的影响较小，且前排桩群对最尾排桩的遮掩效应具有一定的延后性。

2）矩型群桩首排桩的横向水流力对称性分布并不明显，后排桩的分布较为明显。随着桩距的增大，其后排桩这种“两头大，中间小”的分布规律趋于均匀化，但最尾排桩仍有一定的延后性。说明随着桩距的增加，群桩引起的两侧水流加速减小，其两侧桩的水流力与中间桩水流力相对均一化。

3）通过对异型群桩研究发现：其纵向及横向水流力与矩型群桩的分布特性并不相同，这与其群桩型式密切相关。并建议实际工程设计中，应采用2D桩距进行异型群桩的基础设计。