面向需求的应用本体不一致诊断方法研究

宋丹辉

(河南科技大学图书馆，河南 洛阳 471023)



·理论探索·

面向需求的应用本体不一致诊断方法研究

宋丹辉

(河南科技大学图书馆，河南 洛阳 471023)

为计算复杂应用本体中非合法蕴含式集合的根本性冲突原因，首先对现有不一致诊断方法进行系统的梳理，然后结合应用本体及其需求特点，分析存在问题与不足，探讨将原本相互孤立的、分别应用在不同诊断工具中的反模式探测法、根辨解法、简洁辨解法之核心算法进行组合、优化的思路与方法。在此基础上，提出一个综合性的启发式简洁根辨解诊断法，阐述其基本思路与具体步骤，并以相关论文中经常使用的实验本体为例，验证方法的有效性。

应用本体；不一致诊断；简洁辨解；根辨解；反模式探测

语义网的发展强化了用户对高质量应用本体的需求。但应用本体开发是一个复杂过程，需要综合使用多种语言构件来描述具体业务约束规则。在描述逻辑复杂性无法改变、开发者素质无法在短时间内提高的前提下，现有开发方法又普遍缺乏对本体评价、尤其是面向需求的功能评价的支持，这使得本体很容易出现各种不一致问题，严重影响语义正确性及后续推理服务的质量。

从性质上看，这不一致既可能是与本体逻辑基础不符的内部错误(不可满足概念UC)，也可能是与背景知识、领域基本假定不符的潜在语义错误(错误的推论)。且都是经推理才能得到的隐含知识，无法直接删除。只有先识别其可能的产生原因、逐一修正才能彻底消除，这便是应用本体诊断的核心内容[1]。

不同研究者先后提出多种不一致诊断方法，如反模式探测法[2-5]、根辨解法[6]和简洁辨解法[7-9]等。这些方法虽然从不同角度不同程度改善了本体诊断的性能，但就复杂应用本体及其多样化需求而言，仍存在各种局限与不足。目前仍没有一套完整的、既解决内部不一致、也消除潜在语义错误的本体不一致诊断流程或方法，这给实践造成很多不便。

为弥补上述缺漏，本文首先对现有不一致诊断方法进行系统的梳理，然后结合应用本体及其需求特点，分析存在问题与不足，探讨将反模式探测法、根辨解法、简洁辨解法之核心算法进行优化组合的思路与方法。在此基础上，提出一个综合性的启发式简洁根辨解诊断法，并以相关论文中经常使用的实验本体为例，验证方法的有效性。

1 现有工具存在的问题

本体诊断的首要任务是计算辨解，辨解是导致不一致的最小公理集合[10]，其特点是不可再约简，删除其中任何一个公理，推理机便无法推出错误结论，本文将这种需推理才发现的错误结论称为非合法蕴含式，简称蕴含式。就特定蕴含式而言，辨解可能是一个，也可能是多个。每个辨解代表一个独立的充分条件。要真正消除蕴含式，就必须从每个辨解中至少删除或修改一个公理，这种为消除蕴含式必须删除或修改的最小公理集合就是最小诊断[11]。

辨解可能包含与冲突无关的元素(导致概念不可满足或非合法蕴含式的往往只是公理的部分，并非整个公理)[12]，也可能被其他辨解所屏蔽(某些潜在的冲突原因被其他辨解所掩盖，无法识别)[13]，不同辨解间也可能存在依赖关系[14]，这些都会影响后续计算诊断的效率。只有同时保证简洁性、完备性及不依赖其他辨解的独立性辨解，才能真正反映根本性冲突。本文称这种无冗余、无屏蔽及面向全局独立的辨解为简洁根辨解。

若用蕴含式描述具体需求，那么判断本体是否满足具体需求便可通过检测本体与蕴含式的一致性来实现。在实际应用中，具体需求往往有多个，用于检测一致性的蕴含式也就多个，若要依据具体需求来修正本体，计算该蕴含式集的简洁根辨解就不可避免。然而，理想与现实之间总是存在差距，对应用本体而言，目前还没有任何本体诊断工具能完成该任务。从诊断过程对推理机的依赖程度和所得辨解质量看，各工具的局限主要表现在：

(1)过度依赖推理，没有科学利用前人总结出来的建模经验。现有诊断方法要么完全依赖推理，将效率问题一律推给推理机。产生的后果是：不能在有限时间内给出所有辨解，尤其在UC较多、每个UC含较多MUPS、或不一致本体的复杂情况下，受推理机一致性检测效率的影响；要么完全放弃推理，只考虑常见错误模式，用SPARQL检索式或图搜索算法来探测冲突。产生的后果是：无法找到与模式不匹配的冲突原因，不能保证完备性，都不能兼顾效率和完备性。

(2)只偏重辨解的某方面特性，不能同时保证辨解的简洁性、完备性和全局独立性。只有不遗漏任何辨解，且找到辨解都无冗余、不依赖任何其他辨解的方法才是真正有助于用户理解冲突原因并找到最佳解决方案的理想方法。简洁辨解法虽然能识别屏蔽、排除与冲突无关的元素，但一次只能处理一个不可满足概念。当不可满足概念较多时，需要多轮迭代、构建多颗HStree并将结果组合才可找到所有辨解，其繁琐和复杂程度非普通用户所能容忍；根辨解法虽然能基于多个需求识别必须要消除的关键性冲突原因，保证辨解全局独立性，但却以原本体中公理为对象，会牵连冲突无关元素，也可能有屏蔽，准确性有问题。

总而言之，就复杂应用本体的多个需求而言，目前还没有能同时保证辨解简洁性、完备性和全局独立性的方法。

2 启发式简洁根辨解法

应用本体都是为满足特定需求或任务而建的，公理相对复杂，否定、存在或全称约束多，需求数量多、种类也多，更容易出现公理与需求不符的异常情况，潜藏语义错误。

简洁辨解法与根辨解法偏重于不同方面，有结合可能，若能将二者有机结合，在保证简洁性和完备性的基础上计算根辨解，便可优势互补，锁定主要矛盾的主要方面。此外，计算根辨解不仅需要对测试用例集进行一致性检测，还需要构建HStree，二者都需要频繁的一致性检测。而一致性检测的效率与本体语言复杂度及本体规模有很大关系，本文研究对象是复杂应用本体，规模小但复杂度高。为保证效率，就需要尽量减少调用推理机的次数。

2.1 基本思路

为排除冗余、识别屏蔽，本文添加预处理过程，先对本体进行π(Osplit)结构转化[12]，按规则解析所有被嵌套或隐含的语义，并用原子公理表达后，再执行后续诊断流程。π(Osplit)的本质就是在不添加新概念的前提下，根据概念在不同类公理或表达式中的位置，设置不同的转化规则，并用公理索引号记录转化后公理与原公理的对应关系。转化后，任何复杂公理或表达式都可以按语义弱化为语义最约简的原子公理的集合，保证辨解的简洁性和完备性。

为减少调用推理机的次数，本文以不可满足概念为起点、通过启发式规则来探测反模式，并筛选其中不依赖任何其他冲突的根本性冲突作为下一步处理对象。其依据是导致概念不可满足的原因有两类：约束条件之间不兼容(如表1)；约束条件自身不可满足，且不可满足性会随着子类关系和存在约束传播(如表2，所有不可满足概念的下位类都是不可满足的；只要存在约束的filler不可满足，那么被约束概念一定也是不可满足的。表中规则都是参考这种演化机制制定的)[3]。需要说明的是，本步骤虽然只能找到部分辨解，但有助于开发者理解错误产原因，进而由此及彼分析其他可能错误。

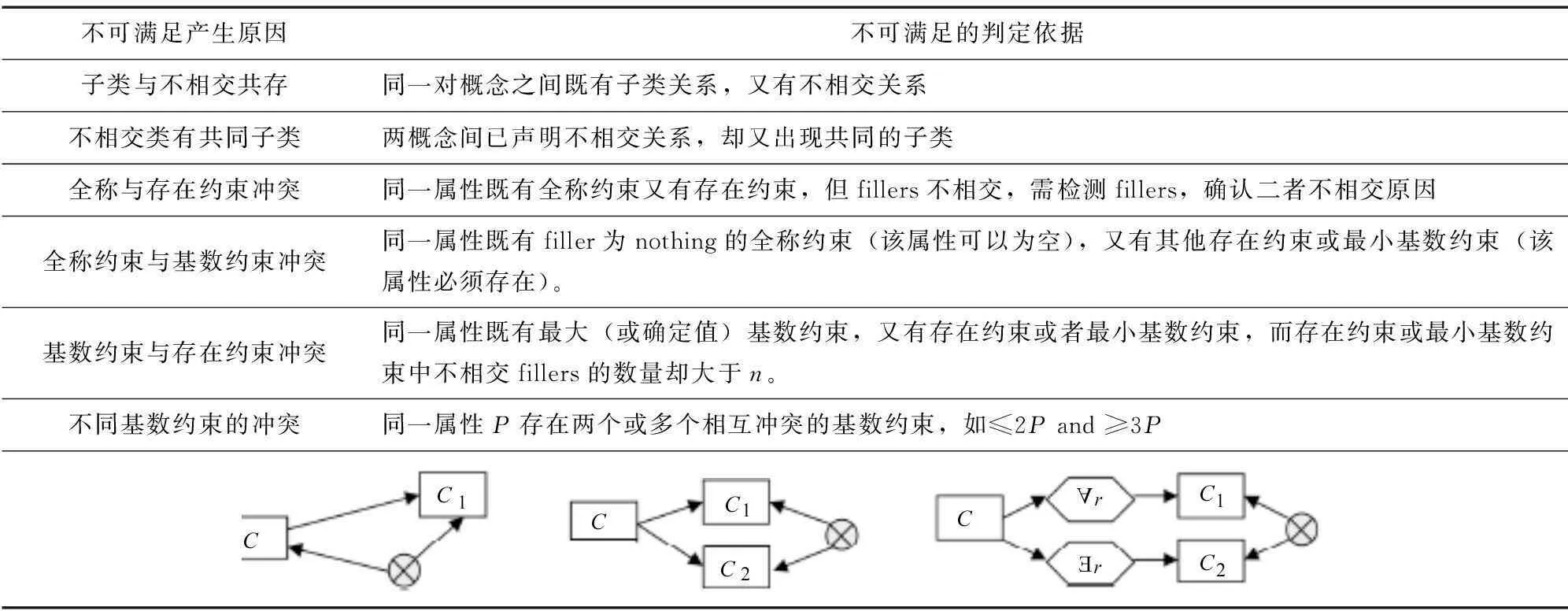
表1 约束条件之间不兼容造成的不可满足及其判定依据

表2 约束条件自身不可满足的判定依据

为保证辨解面向多需求的全局独立性，本文以结构转化后的本体O′为基础，以模式匹配探测到的反模式pdcs为初始化最小冲突集Conf，以代表需求的B∪P∪

N(B代表肯定正确的、不能出现在诊断中的背景理论，P代表必须被目标本体所蕴含的句子集合，N代表一定不能被目标本体所蕴含的句子集合)为判定条件，以quickXplain算法(其性能比滑动窗口法更优)及批量一致性检测来计算与需求不符的根本性最小冲突集(也就是阻碍需求得以满足的非合法蕴含式集合的单个根辨解)，应用路径提前封闭和节点重用技术，宽度优先构建并扩展HStree，真正实现在一颗HStree中找到所有简洁根辨解[15-16]。

考虑到反模式探测也需要原子公理，故先将O进行π(Osplit)结构转化，再用启发式规则探测反模式。反模式探测结果pdcs用于初始化HStree的最小冲突集Conf。需要注意的是，探测结果并非都是根本性的，为确保辨解的全局独立性，本文添加过滤环节，只筛选不依赖任何其他冲突的根本性冲突存入pdcs作为下一步的处理对象。凡不可满足概念UC与两个冲突概念间路径有交集、或者是其他冲突真超集的冲突都非最简，直接被舍弃。

整个流程如图1所示，先结构转化、再用启发式规则探测反模式，最后构建HStree。前两个任务只受转化规则和启发式探测规则的制约，与需求无关，不管测试用例如何变化，其结果都是不变的，后者允许添加测试用例，结果会随着测试用例的变化而变化。

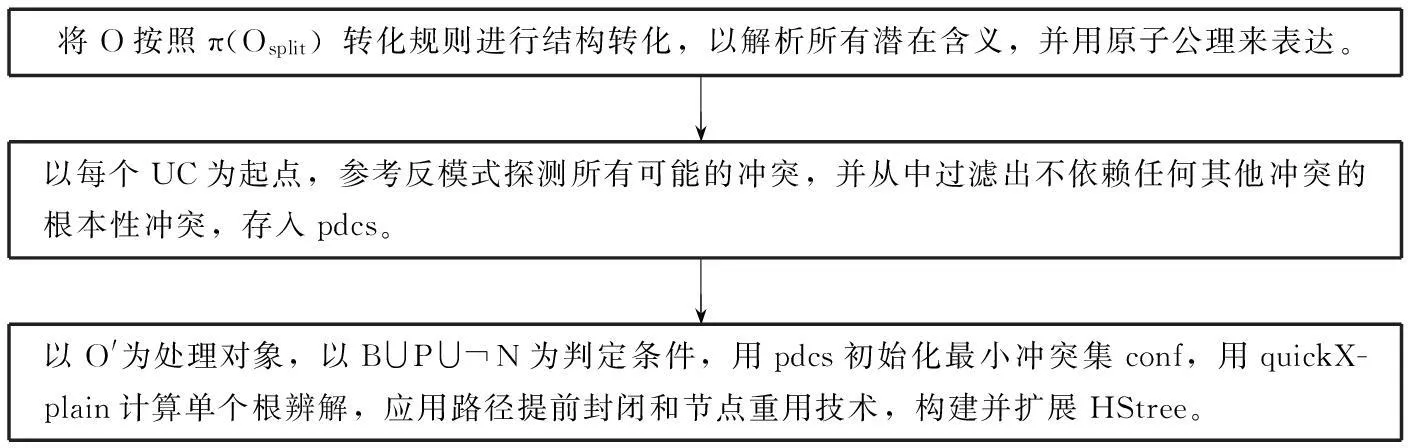
图1 启发式简洁根辨解法的基本思路

2.2 核心步骤

上述流程的重点是第三步，其基本流程如图2。对于根节点，用pdcs初始化最小冲突集Conf。若存在这样的冲突集Conf，则从Conf中任取一个cs作为根节点标识符，针对其中每个公理，扩展新分支，生成新路径(根据辨解定义，删除cs中的任一公理都可以消除该冲突，因此要遍历每个公理，并且都进行扩展)。若pdcs为空，不存在任何反模式，最小冲突集Conf为空，则直接用quickXplain计算与需求不符的最小冲突集srj做为根节点。

图2 构建HStree的基本流程

判断新生成path是否需要提前封闭的规则是：

(1)若存在达到一致的路径H(n)⊆H(n′)或者H(n)=H(n′)，则封闭n′。换句话说，若H(n′)是HS中某个已有最小击中集H(n)的真超集或者与某条已生成路径H(n)相同，则提前封闭该路径；

(2)若不存在这样的路径H(n)，则以当前路径为参数，考察是否存在可重用的节点标识。

判断是否有可重用节点标识的规则是：

(1)若存在标引其他节点的CS(n)，满足CS(n)∩H(n′)=⊥，则重用该CS(n)标引n′。换句话说，若存在某节点的标识符或最小冲突集cs与当前路径无交集，则用其标引当前新节点；

(2)若没有可重用的节点标识CS(n)，则调用推理机，用quickXplain算法结合B∪P∪

N重新生成新的CS(n′)；

(3)若没有满足上述条件的CS(n′)，则表明冲突已消除，无需再扩展，用√来结束该分支。该节点到根节点的路径H(n)可作为新的最小击中集存入HS。

扩展新节点的基本规则是：对于新节点，遍历其公理，扩展新分支，生成新路径。重复上述两个判定过程，直到出现规定数量的叶节点或者所有根辨解和最小击中集为止。

综上，该步骤的本质就是将初始最小冲突集Conf、计算单个根辨解方法quickXplain与HG路径扩展法相结合，先遍历当前最小冲突集cs中公理、依次扩展出新的边，然后针对每条边构建新的路径path′，并参考已有最小击中集和最小冲突集，判断path′是否有真子集、是否有相同路径、是否有不相交节点标识符可重用，若有则重用、若没有则基于path′重新计算新的最小冲突集cs′的循环过程。

所得最小诊断的最小性是最小冲突集、路径提前封闭、节点重用和宽度优先搜索策略共同作用的结果。先生成最小诊断的基数一定是最小的。后续得到最小诊断则会随着HStree的层数而增长。所得最小诊断的正确性和完备性则取决于HStree算法、quickXplain、一致性检测的正确性与完备性。

2.3 效率分析

从效率上看，提高效率的关键点主要有两个：一个是用pdcs初始化HStree的最小冲突集，减少调用推理机的次数；一个是在扩展同一分支过程中，用递减式策略处理P中的需求e+。而降低效率的关键点也有两个：一是预处理中的π(Osplit)结构转化；二是反模式探测。

在quickXplain算法中，要计算节点n的最小冲突集，就需要检测是否存在使需求e+∈P不可满足的非合法蕴含式η，使得(O-path)∪B∪e+∪

N不一致。若存在，则计算其根辨解。对于n的后继节点n′而言，任何已被父节点满足的需求，也就是(O-path)∪B∪e+∪

N一致的e+都无需再考虑。这是因为，子节点路径是父节点路径的真超集(path⊆path′)，那么子节点本体一定是父节点本体的真子集(O-path′⊆O-path)，已在父本体中消除的非合法蕴含式在子本体中一定也不存在，换句话说，在父本体中可满足的需求在子本体中一定也是可满足的。若用集合CE(n)为每个节点n存储所有的与O-path∪B∪e+∪

N一致的e+，那么就新生成节点n′而言，只需检测P-∪m∈predecessor(n′)CE(m)中是否存在与(O-path′)∪B∪e+∪

N不一致的e+便可。该策略可进一步提高算法的性能[17]。

3 实证研究

为验证方法的有效性，本节分别以相关论文中经常使用的两个实验本体为例，阐述启发式简洁根辨解法在计算与需求不符的最小冲突集以及可能解决方案中的具体步骤和方法。

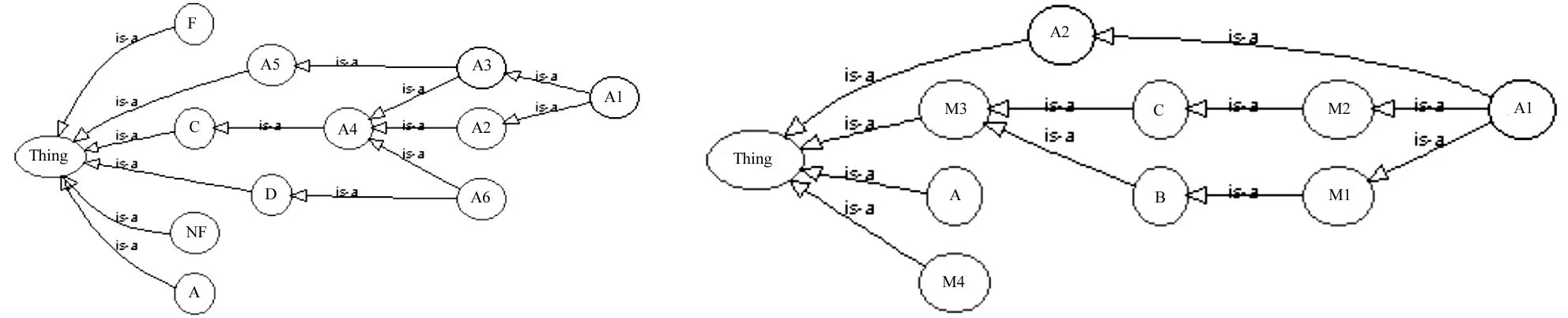
图3 实验本体O1和O2的缩略图

3.1 实验过程

先初始化O，B，P，N，检测B∪P∪N的一致性。实验本体的相关参数见表3。

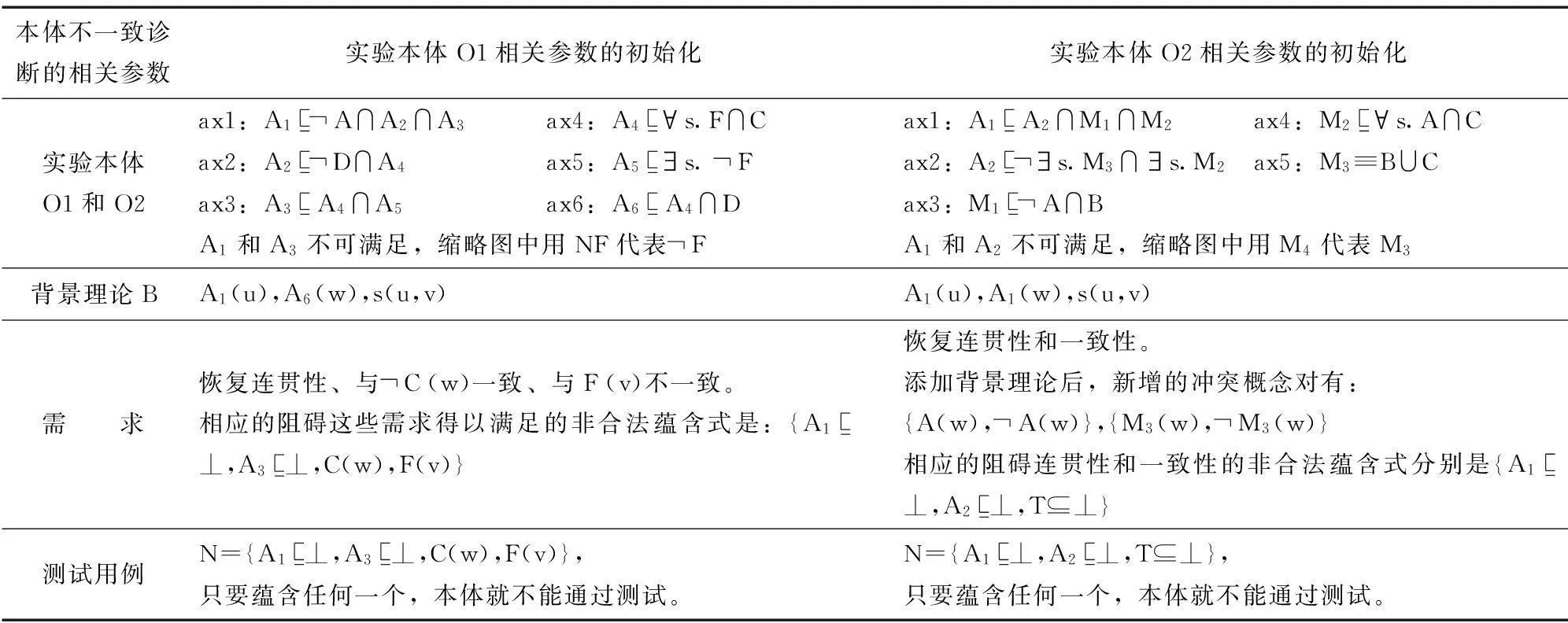
表3 实验本体及其在不一致诊断过程中的相关参数

步骤1：将O按照π(Osplit)转化规则进行结构转化。基于转化后本体O′探测反模式，获取不依赖其他冲突的根本性冲突集pdcs。

O1和O2都有反模式：同一概念同一属性上∃∀冲突，且都随着分类关系进一步衍化。

就O1而言，其具体表现是〈A3

A4，A4

∀s.F，A3

A5，A5

∃s.

F〉，这是造成A3⊆⊥的原因。换句话说，以A3为起点，得出相互矛盾的结论{A3

∀s.F，A3

∃s.

F}。A1是A3的子类，受A3影响，A1也是不可满足的，但造成A1⊆⊥的真正原因有2个：〈A1

A3，A3

A4，A4

∀s.F，A3

A5，A5

∃s.

F〉和〈A1

A2，A2

A4，A4

∀s.F，A1

A3，A3

A5，A5

∃s.

F〉。前者是A3⊆⊥辨解的真超集(或者说A1到冲突概念对F和

F的路径有交集A1

A3)，只要解决A3⊆⊥，该辨解自然就不存在。不是根本性原因，因而直接被排除；后者改变A1到F的路径，不是从A3

A4再到F，而是从A2

A4再到F，这是经结构转化后才能发现的被屏蔽辨解。在原本体中，其对应的公理集合是〈ax1，ax2，ax3，ax4，ax5〉，被A3⊆⊥的常规辨解〈ax3，ax4，ax5〉所归并。经结构转化、排除无关元素后，该冲突与A3⊆⊥的简洁辨解〈A3

A4，A4

∀s.F，A3

A5，A5

∃s.

F〉已不存在包含关系，因而不会被归并(如删除A3

A4后，A3⊆⊥消失，但该冲突仍然存在)，作为新发现根本性冲突加入pdcs。综上，实验本体O1的UC有2个，造成其不可满足的根本原因有2个，最终存入pdcs的结果有2个。

就O2而言，其具体表现是〈A2

∃s.M3，A2

∃s.M2，M2

C，C⊆M3〉，这是造成A2⊆⊥的根本原因。A1是A2的子类，受A1影响，A1也是不可满足的，造成A1⊆⊥的原因有1个〈A1

A2，A2

∃s.M3，A2

∃s.M2，M2

C，C⊆M3〉，是A2⊆⊥辨解的真超集。只要解决A2⊆⊥，A1⊆⊥自然就不存在。不是根本性原因，因而直接被排除。需要注意的是，A1到M3还有另外2条路径，如先到M2然后由M2经C到M3，或者先到M1然后由M1经B到M3，但这2条路径在性质上不同于先到A2然后由A2经M2和C到M3，前者建立的是子类关系A1

M3，后者建立的是属性约束A1

∃s.M3，只有属性约束才能与反模式匹配。添加背景知识后，这种差别将被实例断言掩盖。不管是子类关系还是属性关系，只要使得冲突断言对{M3(w)，

M3(w)}同时存在，便是与需求不符的最小冲突集。因此只有在添加实例断言的条件下，这2条路径才能作为根本性原因加入简洁根辨解中，详情请看步骤3。综上，实验本体O2的不可满足概念有2个，但造成其不可满足的根本原因却只有1个，因此最终只返回1个结果〈A2

∃s.M3，A2

∃s.M2，M2

C，C⊆M3〉存入pdcs。

步骤2：得到O′和pdcs后，预处理过程结束。需求是动态添加的，与需求不符的冲突相对复杂，没有固定的模式，因而不能用启发式规则，必须调用推理机、用quickXplain算法来计算。具体来说，就是以O′为处理对象，以B∪P∪

N为判定条件，用pdcs初始化最小冲突集Conf，用quickXplain计算单个根辨解，应用路径提前封闭和节点重用技术，构建并扩展HStree，获取简洁根辨解CS及最小诊断D。

O1、O2在结构转化、反模式探测及调用HStree方法计算简洁根辨解步骤中的结果见表4：

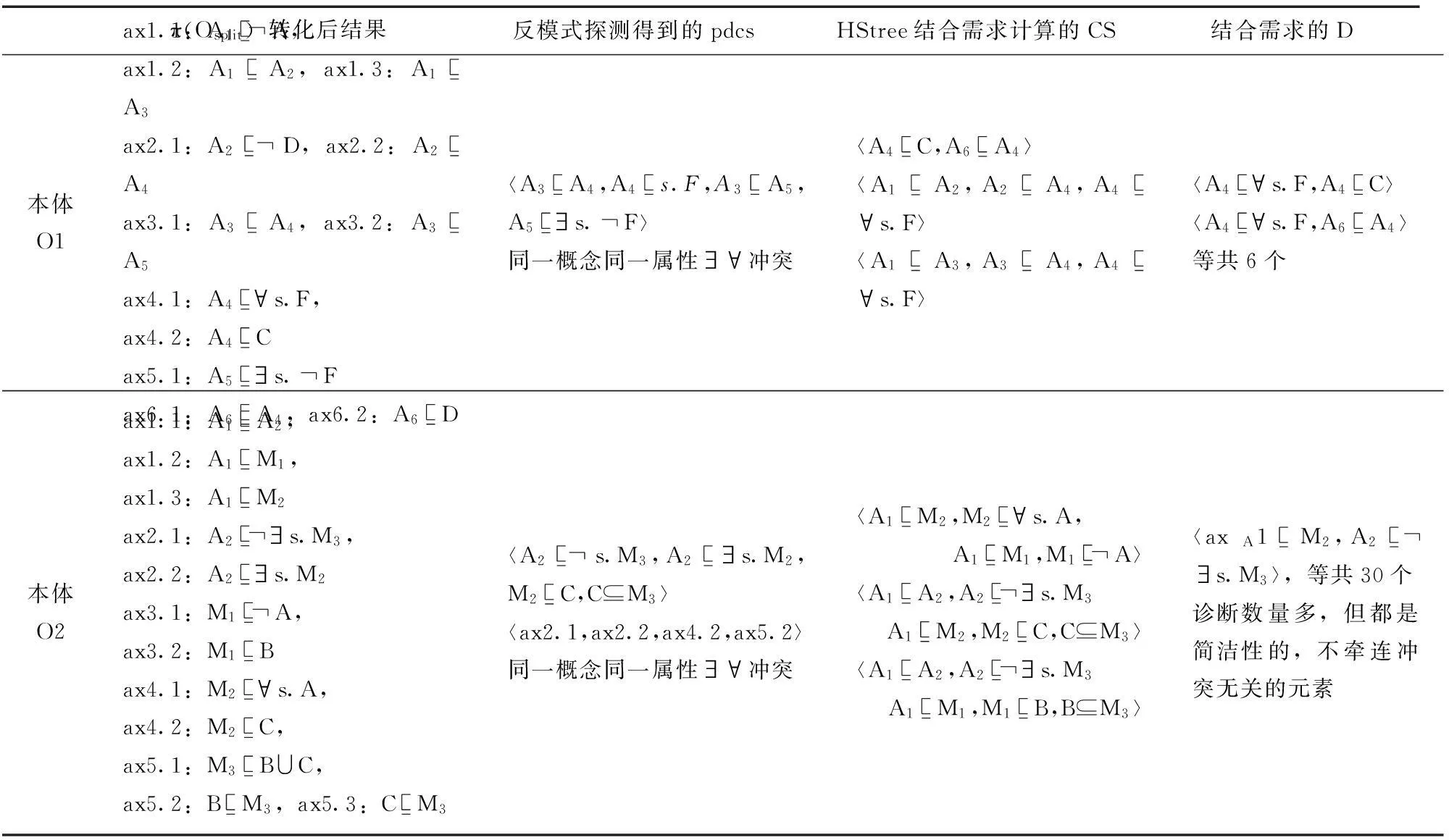
表4 实验本体在结构转化、反模式探测及计算简洁根辨解步骤中的计算结果

就O1而言，添加背景知识B={A1(u)，A6(w)，s(u，w)}后，调用HStree方法计算与需求不符的最小冲突集，也就是非合法蕴含式{A1⊆⊥，A3⊆⊥，C(w)，F(v)}的简洁根辨解。结果共4个，其中{A3⊆⊥}的1个、C(w)的1个、F(v)的2个。需要注意的是，反模式探测结果原本有2个，但其中之一{A1⊆⊥}的简洁辨解〈A1

A2，A2

A4，A4

∀s.F，A1

A3，A3

A5，A5

∃s.F〉被F(v)的简洁根辨解〈A1

A2，A2

A4，A4

∀s.F〉所归并。在路径提前封闭和节点重用技术的帮助下，用这4个最小冲突集共生成6个最小诊断。除表中列出的2个外，还有另外4个{〈ax1.2，ax3.1〉，〈ax2.2，ax3.1〉，〈ax1.2，ax1.3〉，〈ax2.2，ax1.3〉}。

就O2而言，添加背景知识B={A1(u)，A1(w)，s(u，w)}后，调用HStree方法计算与需求不符的最小冲突集，也就是非合法蕴含式{A1⊆⊥，A2⊆⊥，{A(w)，

A(w)}，{M3(w)，

M3(w)}}的简洁根辨解。结果共4个，其中{A2⊆⊥}的1个，{A(w)，

A(w)}的1个、{M3(w)，

M3(w)}的2个。造成{M3(w)，

M3(w)}的原因原本有3个：其中1个是〈A1

A2，A2

∃s.M3，A2

∃s.M2，M2

C，C⊆M3〉，另2个是〈A1

A2，A2

∃s.M3，A2

∃s.M2，M2

C，C⊆M3〉和〈A1

A2，A2

∃s.M3，A1

M1，M1

B，B⊆M3〉。前者被A2⊆⊥的简洁辨解归并；后两种改变A1到M3的路径，不是先由A1

A2得A2(u)、然后从A2

∃s.M2得M2(w)、再由M2经C推出M3(w)，而是先由A1

M2得M2(w)、再由M2经C推出M3(w)；或者从由A1

M1得M1(w)、再由M1经B推出M3(w)，A1到冲突概念对M3(w)和

M3(w)的路径无交集，不依赖任何其他冲突，都是根本性原因，因而都加入最终结果。

需注意的是，〈A1

A2，A2

A4，A4

∀s.F，A1

A3，A3

A5，A5

∃s.

F3〉是经结构转化后才发现的辨解。在原本体中，其对应的常规辨解是〈ax1，ax2，ax4，ax5〉，不仅与A1⊆⊥的常规辨解完全相同，还会被A2⊆⊥的常规辨解〈ax2，ax4，ax5〉所归并，因此{M3(w)，

M3(w)}的根辨解只有1个。经结构转化、排除无关元素后，该冲突与〈ax2，ax4，ax5〉所对应的简洁根辨解〈A2

∃s.M3，A2

∃s.M2，M2

C，C

M3〉已不存在包含关系，因而不会被归并(如删除A2

∃s.M2后，前一个冲突消失，但该冲突仍然存在)，{M3(w)，

M3(w)}的根辨解数由1变为2。在路径提前封闭和节点重用技术的支持下，用这4个最小冲突集共生成30个最小诊断。

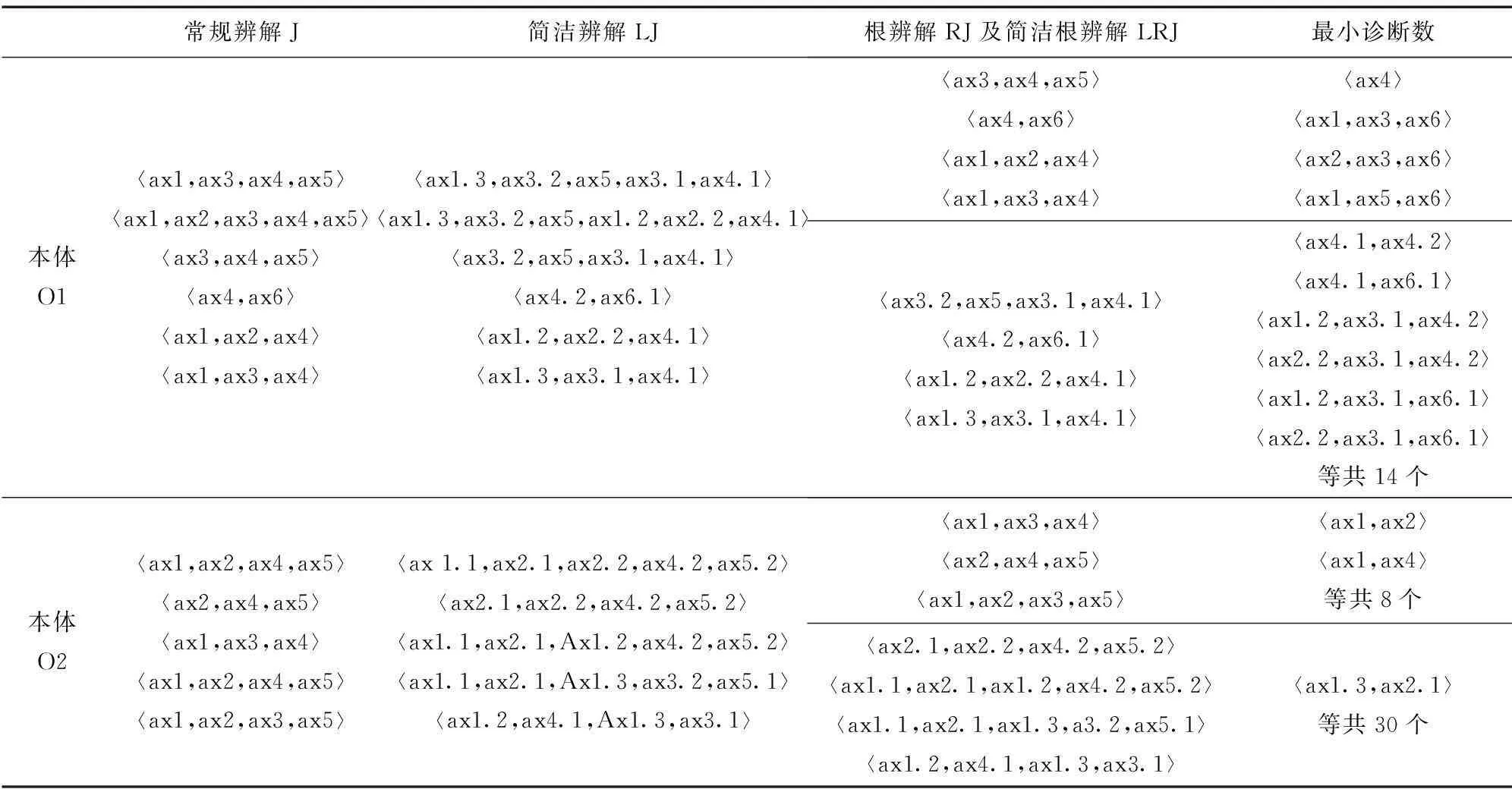
表5 实验本体中各类辨解及最小诊断的构成

参考表5，实验本体O1中各类辨解的分布情况以及简洁根辨解示意图如图4所示：A1⊆⊥有2个不简洁辨解，但都被A3⊆⊥归并，有1个也可以被F(v)的辨解归并，因此根辨解和简洁根辨解都变为0；A3⊆⊥和C(w)各有1个不简洁根辨解。结构转化后，各生成1个简洁根辨解；F(v)有2个不简洁根辨解。结构转化后，生成2个简洁根辨解。

参考表5，实验本体O2中各类辨解的分布情况以及简洁根辨解示意图如下图所示：A1⊆⊥有1个不简洁辨解，但被A2⊆⊥归并，因此根辨解和简洁根辨解都变为0；A2⊆⊥和{A(w)，

A(w)}各有1个不简洁根辨解。结构转化后，各生成1个简洁根辨解；{M3(w)，

M3(w)}有2个常规辨解，其中1个被A2⊆⊥归并，只剩下1个根辨解。结构转化后，生成3个简洁辨解，真正能被A2⊆⊥简洁根辨解归并的只有1个，因此最终简洁根辨解数为2。

图4 实验本体O1中各类辨解的分布情况以及简洁根辨解示意图

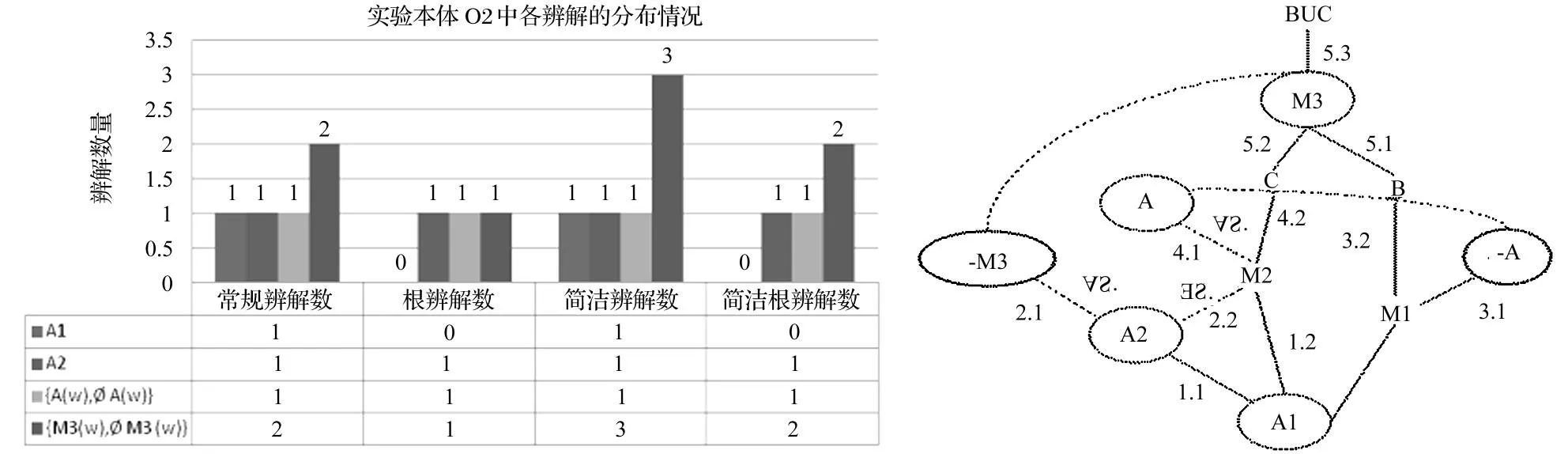
图5 实验本体O2中各类辨解的分布情况以及简洁根辨解示意图

需要注意的是，在{M3(w)，

M3(w)}的2个常规辨解中，被A2⊆⊥归并的恰恰也是A1⊆⊥的常规辨解，因此常规辨解总数是4，并不是5；同理，在{M3(w)，

M3(w)}的3个简洁辨解中，被A2⊆⊥归并的恰恰也是A1⊆⊥的简洁辨解，因此简洁辨解总数是5，并不是6。

3.2 结果分析

从归并和屏蔽的关系看，屏蔽就是错误的归并。两辨解的公理虽然相同或存在包含关系，但真正用于推理的元素却不同。若基于原本体中复杂公理直接求根辨解，这种差异就会被掩盖，原本不能被归并的辨解就会错误的被归并(如实验本体O1中A1的辨解)；归并就是有意的屏蔽，根据依赖关系，把本质上相同的辨解都归结为一个关键性冲突，减少处理问题的数量，以提高效率、集中力量解决主要矛盾(如结构转化后，上述A1的辨解虽然不再错误的被A2屏蔽，但最终又被F(v)的辨解所归并)。

结构转化可以识别被屏蔽辨解。同一个蕴含式的不同辨解间可能有屏蔽，不同蕴含式的辨解间也可能有屏蔽。公理间的关联关系是错综复杂的，与蕴含式的作用关系也是复杂的，只有通过结构转化，把相关的复杂公理都分解为原子公理，把所有的嵌套的语义都解析出来，才能明确这种相互作用关系，避免任何可能的屏蔽。

结构转化是否会影响归并辨解数并不清晰，有待进一步研究。但可以肯定，这7类辨解的数量关系应满足表6。

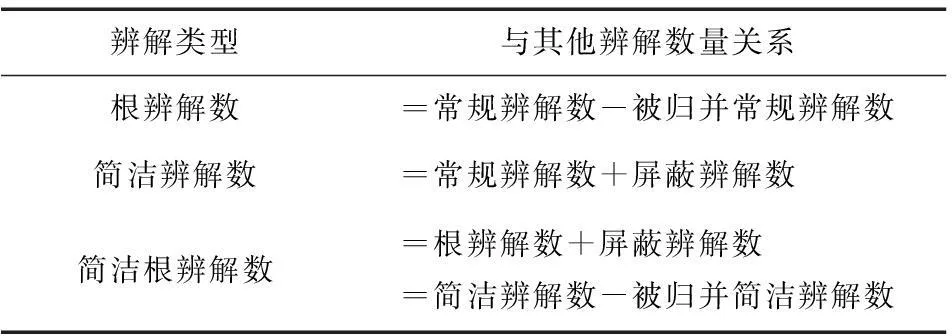
表6 7类辨解的数量关系表

将上述实验结果汇总，将简洁根辨解数分别与其他辨解数对比，可得组图6。由图中数量变化关系可以看出，实验结果与上表完全吻合，这间接表明启发式简洁根辨解法在揭示根本性冲突上的准确性。

综上，简洁根辨解不同于简洁辨解，也不同于根辨解，更不同于常规辨解。大部分情况下，简洁根辨解数都小于常规辨解数。仅在每个不可满足概念都有独立辨解、或存在被屏蔽辨解时，简洁根辨解数才会大于常规辨解数。只要常规辨解数与简洁辨解数不等(通常是小于)，就说明有屏蔽，存在其他被掩盖的冲突原因；只要常规辨解数与根辨解数不等(通常是大于)，就说明辨解间有依赖关系，真正需要处理的冲突原因要少一些。而简洁根辨解数则是找出屏蔽、归并衍生性冲突之后的结果，大部分情况下都小于常规辨解数。仅在有不能被归并的屏蔽辨解时，简洁根辨解数才可能大于常规辨解数。

图6 实验对象各类辨解对比图

3.3 与其他工具的对比

为验证方法在准确性上的优势，下文以实验本体O1为例，分别用SWOOP(常规辨解法)[18]、Protege and Debugger(根辨解法)[19]、ORE(简洁辨解法)[20]、启发式简洁根辨解法对其进行诊断，并对比分析其结果。

常规辨解法：以N={A1

⊥，A3

⊥，C(w)，F(v)}为非合法蕴含式集合，用传统方法计算辨解及诊断的过程较复杂，具体过程如下：先识别根不可满足概念A3，计算一个MUPS作为根节点构建HStree，计算其他最小冲突集CS1(如〈ax3，ax4，ax5〉)和最小诊断D1(如{〈ax3〉，〈ax4〉，〈ax5〉})。然后分别删除不同的d1，得到连贯本体集Ot1。将Ot1与需求2合并，识别冲突，构建HStree，计算最小冲突集CS2(如{〈ax4〉，〈ax6〉})和最小诊断D2(如〈ax4〉或〈ax6〉，〈ax4〉也是第一棵树的诊断，删除〈ax4〉后需求2是满足的，此时不会增加新的诊断。但删除其他两个诊断〈ax3〉或〈ax5〉后需求2不满足，算法会重新计算出〈ax6〉和〈ax4〉)。然后分别删除不同的d2，得到满足前两个需求的候选本体集Ot2。依次类推，最后得到与需求3不符的最小冲突集CS3(如〈ax1，ax2，ax4〉，〈ax1，ax3，ax4〉)和消除冲突所需的最小诊断D3(如〈ax1〉，〈ax4〉或〈ax2，ax3〉)。将D1，D2，D3组合，才能得到最终的4个诊断。总的来说，传统方法一次只能选择1个RUC计算其辨解。当RUC较多时，前后需要构建多棵HStree才能计算出所有辨解。将这些辨解按照包含关系归并，才能得到N的根辨解，但并不保证简洁性。计算最小诊断随着计算辨解而完成，且是逐步累积的，需要分别将每颗树中的最小诊断组合才能得到一次消除所有N的最小诊断。这个最小诊断并非并非最小，还可能包含与冲突无关的元素。传统诊断法并不一定能求出简洁根辨解。

根辨解法：如图7所示，以N={A1⊆⊥，A3⊆⊥，C(w)，F(v)}为非合法蕴含式集合，用根辨解法只需一棵HStree树便可计算4个最小冲突集和4个最小诊断。虽然考虑多个需求，效率相对较高，但不考虑辨解和最小诊断的简洁性，会误删与冲突无关的元素。比如，就诊断〈ax1，ax3，ax6〉而言，删除〈ax1.2，ax3.1，ax6.1〉就可以达到满足所有需求的目的，〈ax1.3，ax3.2，ax6.2〉都是可以保留的，这便是简洁根辨解法相对于根辨解法的优势所在。

简洁辨解法：以N={A1

⊥，A3

⊥，C(w)，F(v)}为非合法蕴含式集合，与传统方法类似，虽然能排除冗余、避免屏蔽，但一次只处理一个需求，需要分别针对每个非合法

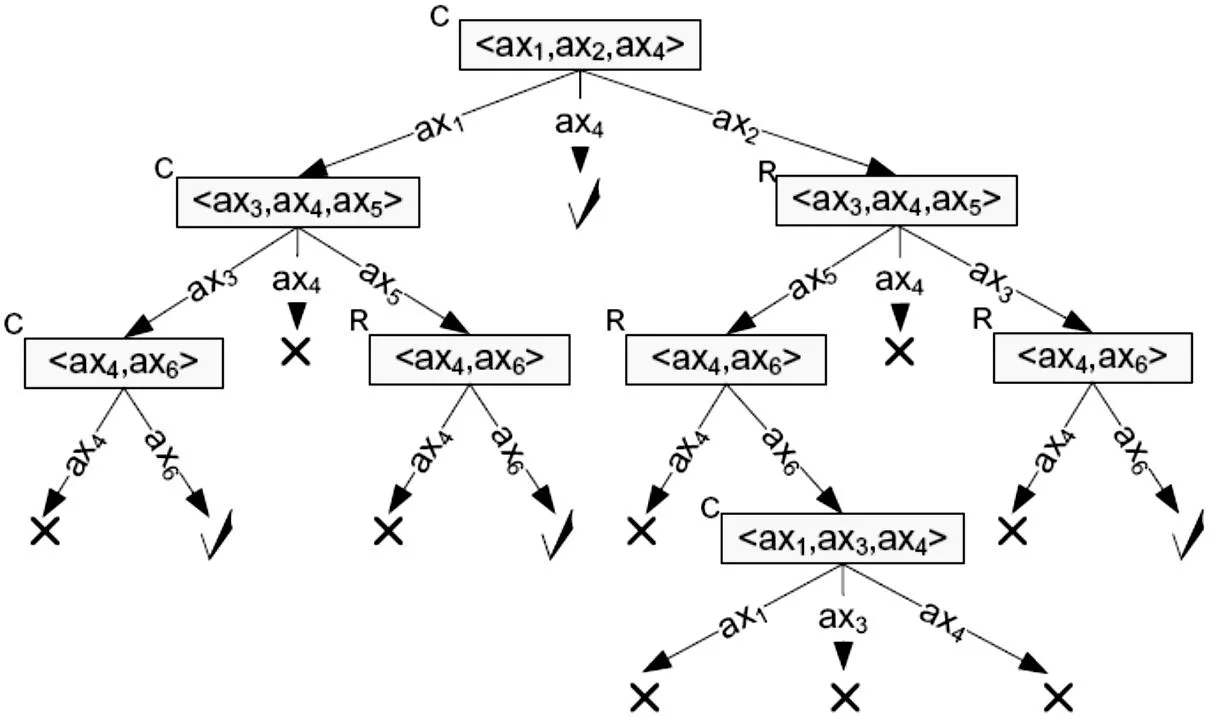
图7 用根辨解法处理实验本体O1示意图

蕴含式计算其所有简洁辨解，然后将这些辨解按照包含关系归并，才能最终得到N的简洁根辨解。计算最小诊断随着计算辨解而完成，需要构建多颗HStree并将中间结果组合，才能得到能一次消除所有N的最小诊断。其繁琐和复杂程度非普通用户所能容忍。

简洁根辨解法：如图8所示，以N={A1

⊥，A3

⊥，C(w)，F(v)}为非合法蕴含式集合，用简洁根辨解法，先探测到一个根本性反模式实例〈ax3.1，ax3.2，ax4.1，ax5〉，以其为根节点构建并扩展HStee，得到其它3个最小冲突集和14个最小诊断，其中最小基数诊断有2个。传统方法和根辨解法都只能得出〈ax4〉1个最小基数诊断，但简洁根辨解法可以得到2个，多出一种诊断方案来，用户可根据自身要求决定留4.2(A4⊆C)还是6.2(A6⊆D)。最小诊断数量虽然较多，但都是细简洁性的，不牵连与冲突无关的元素。

图8 用简洁根辨解法处理实验本体O1示意图

将上述实验结果汇总，可得表7。由表中对比可以看出，就复杂本体的非合法蕴含式集合S而言，常规辨解法和根辨解法并不一定能求出其简洁根辨解，简洁辨解法虽然能最终求出简洁根辨解、但需多轮迭代并将中间结果组合，过程太过繁琐，不具有可行性，只有本文提出启发式简洁根辨解法能求出所有的简洁根辨解。

表7 不同诊断方法特点及其在处理实验本体O1中的表现

表7(续)

4 结 论

为计算复杂应用本体中的非合法蕴含式集合的根本性冲突原因，本文将原本相互孤立、分别用于反模式法、根辨解法和简洁辨解法的核心技术：启发式规则、批量一致性检测、结构转化有机组合，提出简洁根辨解的概念(与根本性冲突原因存在一一对应关系)以及能计算该类辨解的启发式简洁根辨解法，阐述其基本思路与流程，探讨其实现方法。在此基础上，用相关文献中经常使用的本体为例验证方法的可行性与有效性，分析简洁根辨解与其他类辨解间的区别与联系，并将启发式简洁根辨解法与其他诊断方法进行对比，分析结果的准确性，分析其对最小诊断数的影响。实践证明，这种在组合原有方法基础上得到的启发式简洁根辨解法可以完成任务一，不管本体自身是否简洁、不管需求有几类，都可以找到根本性最小冲突集，同时保证辨解的完备性、简洁性和准确性，为后续筛选目标诊断奠定良好基础。

[1]SchlobachS,Huang Z.Inconsistent ontology diagnosis:Framework and prototype[J].Deliverable D3.6.1,SEKT，2005:15-25.

[2]Ji Q,Gao Z,Huang Z,et al.An efficient approach to debugging ontologies based on patterns[M].The Semantic Web.Springer Berlin Heidelberg,2012:425-433.

[3]Wang H.,Horridge M.,Rector A.L.,etal.Debugging OWL-DL Ontologies:A Heuristic Approach[M].In:Gil Y.,Motta E.,BenjaminsV.R.,et al.ISWC 2005,LNCS 3729,Springer,Heidelberg,2005:745-757.

[4]Lam S C J,Sleeman D,Vasconcelos W.Graph-Based Ontology Checking.In Proceedings KCAP05 workshop on Ontology Management: Searching,Selection,Ranking and Segmentation,Banff,Canada,2005:33-40.

[5]Roussey C,Corcho O,Vilches-Blázquez L M.A catalogue of OWL ontology antipatterns[C].∥Proceedings of the fifth international conference on Knowledge capture.ACM,2009:205-206.

[6]Meyer T,Moodley K,Varzinczak I.First steps in the computation of root justifications[C].∥Proceedings of ARCOE 2010.

[7]Lam S C,Pan J Z,Sleeman D,et al.A fine-grained approach to resolving unsatisfiable ontologies[C].∥Proceedings of Web Intelligence,2006.WI 2006.IEEE/WIC/ACM International Conference on.IEEE,2006:428-434.

[8]HorridgeM,ParsiaB,SattlerU.Laconic and precise justifications in OWL[C].∥Proceedings of the 7th International Semantic Web Conference(ISWC-2008),LNCS,Springer-Verlag,2008，(5318):323-338.

[9]HorridgeM.Justification based explanation in ontologies[D].the University of Manchester,2011:140-193．

[10]Kalyanpur A,Parsia B,Grau B C,et al.Justifications for entailments in expressive description logics[R].Technical report,University of Maryland Institute for Advanced Computer Studies(UMIACS),2006.

[11]SchlobachS,Cornet R.Non-standard reasoning services for the debugging of description logic terminologies[C].∥Proceedings of the 18th International Joint Conference on Artificial Intelligence(IJCAI-2003),2003:355-360.

[12]Horridge M,Parsia B,Sattler U.Explaining inconsistencies in OWL ontologies[M].Scalable Uncertainty Management.Springer Berlin Heidelberg,2009:124-137．

[3]Horridge M,Parsia B,Sattler U.Justification Masking in Ontologies[C].∥Proceedings of Thirteenth International Conference on the Principles of Knowledge Representation and Reasoning，2012.

[14]Kalyanpur A,Parsia B,Sirin E,et al.Debugging unsatisfiable classes in OWL ontologies[J].Web Semantics:Science,Services and Agents on the World Wide Web,2005,3(4):268-293.

[5]Junker U.QUICKXPLAIN:preferred explanations and relaxations for over-constrained problems[C].∥Proceedings of the National Conference on Artificial Intelligence.Menlo Park,CA;Cambridge,MA;London;AAAI Press;MIT Press;1999,2004:167-172.

[16]Shchekotykhin K,Friedrich G,Jannach D.On computing minimal conflicts for ontology debugging[J].Model-Based Systems,2008，(7):7-12.

[17]Shchekotykhin K.,Friedrich G.,Fleiss P.,et al.Interactive ontology debugging:two query strategies for efficient fault localization[J].Web Semantics:Science,Services and Agents on the World Wide Web,2012，(12-13):88-103.

[18]KalyanpurA,ParsiaB,SirinE,etal.Swoop:A web ontology editing browser[J].Web Semantics:Science,Services and Agents on the World Wide Web,2006,4(2):144-153.Springer,Heidelberg,2005:745-757.

[19]ProtegeAndDebugger[EB/OL].http:∥code.google.com/p/rmbd/，2012-12-20.

[20]Lehmann J,Bühmann L.ORE-a tool for repairing and enriching knowledge bases[M].The Semantic Web-ISWC 2010.Springer Berlin Heidelberg,2010:177-193.

(本文责任编辑：孙国雷)

The Research on Requirements-oriented Ontology Inconsistent Diagnosis Method

Song Danhui

(Library，Henan University of Science and Technology，Luoyang 471003，China)

Firstly,the article teased out the existing Inconsistent Diagnosis methods systematically,and then analyzed the existing problems and inadequacies,combining with the characteristics of application ontology and its requirements,and explored new research idea and method to combine and optimize the core algorithms of anti-pattern detection,root justifications,laconic justifications algorithms respectively,which were isolated Originally and applied in different diagnostic tools respectively.Based on this,the paper not only put forward a comprehensive diagnosis method which is called heuristic Laconic Root Justifications,but also pointed out the basic ideas and concrete steps,and put two frequently used experimental ontologies in related study as examples,in order to validate the effectiveness of the method.

application ontology;inconsistent diagnosis;laconic justifications;root justifications;anti-pattern detection

2015-10-20

2013年国家社会科学基金青年项目“数字图书馆用户数据资源化管理研究”(项目编号：13CTQ012)研究成果之一。

宋丹辉(1983-)，女，馆员，研究方向：知识组织，数字图书馆理论与实践。

10．3969/j．issn．1008-0821．2016．03．005

G254.29

A

1008-0821(2016)03-0027-11