微课让数学教学更有效

王涛



有些学生在数学学习过程中表现为越学越差的发展趋向.如何解救这些被数学伤到的学生呢？这是长期困扰数学教师的难题.萨尔曼?可汗认为，这是每个学生学习的步调不一致造成的.有些学生能够凭借直觉理解概念，有些学生要仔细琢磨才能理解概念.所以，他主张翻转课堂，把教师讲的内容、知识点编制成微课，让学生自己看.这样，学生能够按照自己的理解能力，按自己的学习节奏来学习，体现个性化教学的理念.

一、讲授类微课

例如，在讲“整式的加减”时，教师可以设计以下自学质疑学案来引导学生利用微课进行学习.

第一，按照学案提示的步骤自学.

1.仔细阅读，完成后面的问题.一个两位数，个位数字是x，十位数字是y，那么这个两位数怎样表示？如果把这个两位数的个位数字与十位数字交换位置，那么这个新的两位数怎样表示？你能写出这两个两位数的差吗？它有何特点？

2.请同学们用2个大小一样的直角边为b斜边为a的直角三角形，1个长为a、宽为b的长方形拼出各种不同形状的四边形，再分别计算它们的周长.通过计算，它们的周长有相等的吗？有不等的吗？如有不等，你能计算出它们的周长和与差吗？

3.独立完成下列题目，体会整式加减的步骤，形成自己的思路.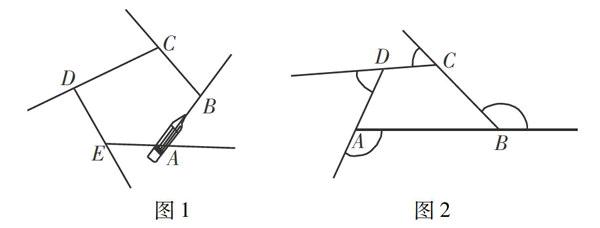

（1）求2a2-4a+1与-3a2+2a-5的差.

（2）求多项式2x－3y＋7与6x－5y－2的和.

（3）求5(3a2b-ab2)-4(-ab2+3a2b)的值，其中a=-2,b=3.

总结：整式加减的步骤.

第二，观看微课“整式的加减”，明确各题的答案，用红笔修改，并在边栏写下对自己做题失误的分析.

自学质疑学案是引导学生学习的方案，是学生课堂学习实践过程中的操作方案，是学生学习活动的“路线图”，引领学习方向.它规定的只是基本路线、基本方法，至于学生学习的速度、深度、广度以及学习的策略和具体细节，由学生自主决定.

讲授类微课，只需一块朴实无华的电子黑板来记录讲课者的声音与笔迹，学习者通过听讲课者的声音（讲课者不出现在影片中），并完整地观看电子黑板上讲课者板书，进而开始学习.微课编制者只有重视教学内容的组织与编排，符合学生的认知逻辑规律，过程主线清晰、重点突出，逻辑性强，明了易懂，才能激发学生的学习兴趣.

二、演示类微课

例如，在讲“多边形的外角和”时，教师可以在设计的自学质疑学案中添加以下问题.

1.如图1，铅笔贴放在五边形ABCDE的边AB上，笔尖方向为点A到点B的方向.把铅笔依次绕点B、C、D、E、A按逆时针方向旋转，铅笔从五边形的一边转到相邻的另一边，笔尖转过的角是哪些？你能在图中把它们表示出来吗？在转动的过程中，笔尖方向发生了怎样的变化？这种变化说明了什么？

2.如图2，将四边形逐步“缩小”时（形状不变），外角和不变，考虑一种特殊情形，当多边形“缩小”成一点时，它的所有外角会组成什么样的图形？

相应的微课，可录制铅笔沿着多边形的边转一圈的动画，设计这样有趣的动画，使学生对学习内容本身发生兴趣.另一个动画是当多边形逐步“缩小”成一点时，它们的所有外角会组成什么样的图形？观看这个动画，能让学生在“缩小”活动中观察、体验，让学生看到了多边形外角和是一个周角，在感性上升到理性的过程中完成数学活动经验的积累，引导学生在“做数学”中“悟数学”，使数学教学更有效.

三、实验类微课

实验类微课对于编制者要求很高，首先他要考虑实验可能出现的所有结果，并对比发现哪个节点会让学生觉得困难；其次要斟酌选取什么样的问题对学生思考具有启发性；最后要启发学生观察实验结果，总结规律并分享一些技巧.

总之，翻转课堂，让学生通过实验探究、合作讨论，不但可以复习之前视频上学到的知识点，还可以运用学到的知识解决问题，提高教学效果.