基于灰色关联分析的仓库危化品危险系数评价

高 飞袁树杰，2

1.安徽理工大学能源与安全学院 2.煤矿安全高效开采省部共建教育部重点实验室

基于灰色关联分析的仓库危化品危险系数评价

高 飞1袁树杰1，2

1.安徽理工大学能源与安全学院 2.煤矿安全高效开采省部共建教育部重点实验室

企业仓库作为企业整体中不可缺少的一部分，其内储存的物品往往关乎企业的发展和壮大。一旦发生火灾或者爆炸，将会对企业造成难以估量的损失，甚至会使企业面临破产或者倒闭风险。本文应用灰色关联分析法对某一个典型火灾爆炸事件进行相应的危化品安全分析，得到仓库危化品的危险系数，为危化品的安全管理提供了参考。

仓库；危化品；灰色关联分析；危险系数 ；层次分析法

仓库作为一个企业储存生产物品的库房，是企业实现效益的最后一道工序，关乎企业的生存、发展和壮大。然而近年来，企业仓库的火灾及爆炸事件却频频发生，企业安全生产令人担忧。2015年8月12日，天津东疆保税港区瑞海国际物流有限公司所属危险品仓库发生爆炸，造成165人遇难，8人失踪，几万户房屋受损，经济损失达数百亿元人民币； 10月12日，天津市天津永晟化工有限公司一储存乙醇、甘油等化工产品的仓库发生大火，无人员伤亡。对于存储化工产品的仓库，其在发生火灾或者爆炸后，将造成无法估量的经济损失和人员伤亡的后果。灰色关联分析法是一种根据因素之间发展趋势的相似或相异程度，即“灰色关联度”，作为衡量因素间关联程度的一种方法［1］。对于危化品，则通过定量确定各项关联指标系数的数值，本文所利用的加权平均数法来对评价对象危险程度进行等级划分，使定量判断更加准确，对于企业做好仓库的防火安全措施具有指导意义。

1　分析方法介绍与应用

1.1灰色关联分析法

灰色关联分析方法，是根据因素之间发展趋势的相似或相异程度，亦即“灰色关联度”，作为衡量因素间关联程度的一种方法［2］。

灰色关联分析法的计算与分析步骤如下［3］：

（1）确定能够反映系统行为特征的参考数列，以及能够影响系统行为的比较数列。

（2）针对以上确定出的参考数列和比较数列，对其进行无量纲化处理。

（3）求解参考数列和比较数列的灰色关联系数ζ（Xi）。

对于一个由若干个比较数列X1， X2，…， Xn组成的参考数列X0，各比较数列与参考数列在各个时刻的关联系数ζi（k）可由下列公式算出：

式中 ：

ρ—分辨系数，在0～1之间，常取0.5；

Δ（min）—第二级最小差；

Δ（max）—两级最大差；

Δ0i（k）—各比较数列上的点Xi与参考数列上的点X0的绝对差值。

（4）求关联度［4-5］。

因为关联系数是比较数列与参考数列在不同情形下的关联程度值，所以往往它具有很多个值，而分散开的不同的数值之间很难进行整体性比较。因此，采取取其算术平均值的方法（有时还因关联系数本身重要性的不同，采用加权取其平均值得方法），将各个的关联系数集中为一个值，作为比较数列与参考数列间关联程度的数量表示，关联度公式如下：

式中：

ri—比较数列xi对参考数列x0的灰关联度；ri的值越接近1，则说明相关性越好。

（5）关联度排序。

依据上述步骤（4）的方法求解出的关联度，将其按照从大到小的顺序排列，得到待评价目标依关联度的排列顺序。

灰色关联度分析法是将研究对象及影响因素的因子值视为一条线上的点，与待识别对象及影响因素的因子值所绘制的曲线进行比较，比较它们之间的贴近度，并分别量化，计算出研究对象与待识别对象各影响因素之间的贴近程度的关联度，通过比较各关联度的大小来判断待识别对象对研究对象的影响程度。

1.2层次分析法

应用单层次一致性检验的方法，检验判断矩阵是否具有满意一致性，检验公式为：

式中：

λmax—通过判断矩阵求得的最大特征值；判断矩阵平均随机一致性指标 RI，见表1。

表1　平均随机一致性指标RI值

计算判断矩阵的一致性比率CR=CI/RI；当CR=0时，A具有完全一致性；当CR＜0.1时，即认为判断矩阵具有满意的一致性，否则需要调整判断矩阵使其达到可接受的一致性比率。

2　分析方法在危化品中的应用

2.1背景

2015的8月12日，在天津东疆保税港区的码头，天津瑞海国际物流有限公司所属的危险品仓库发生了爆炸。根据官方提供的一些危化品数量统计，该公司危化品仓库储存的部分制作成危化品种类和数量统计，见表2。

表2　危化品数量统计表

2.2应用灰色关联分析法进行分析

（1）评价指标的确定。指标的确定可以说是该灰色关联分析法的重点，本文根据文献［6］，了解到，对于危险化工产品，其储存量的体积越大，人员等接触到的可能性就越大；沸点越低，越容易发生火灾或爆炸的危险；半致死量越小，说明其扩散的毒性及危险性越大；当然，其本身是否具有可燃性也很重要，越容易发生燃烧或者爆炸，其存储就越难，越易发生危险；最后就是，该化工产品遇水会产生怎样的反应亦需要考虑，这可以防止在发生火灾时，因盲目的的用水灭火而造成更大损失。

为更好的确定各种危化品危险程度，本文确定了以下评价指标：比值R（储存量/临界值），体积V，沸点BP，半致死量LD50，可燃/爆炸C/B，遇水反应WR。

（2）对指标数据进行无量纲化。利用插值法对以上的数据按指定的评价指标进行Min-max标准化后，在进行百分制无量纲化。危化品数量无量纲化统计，见表3。

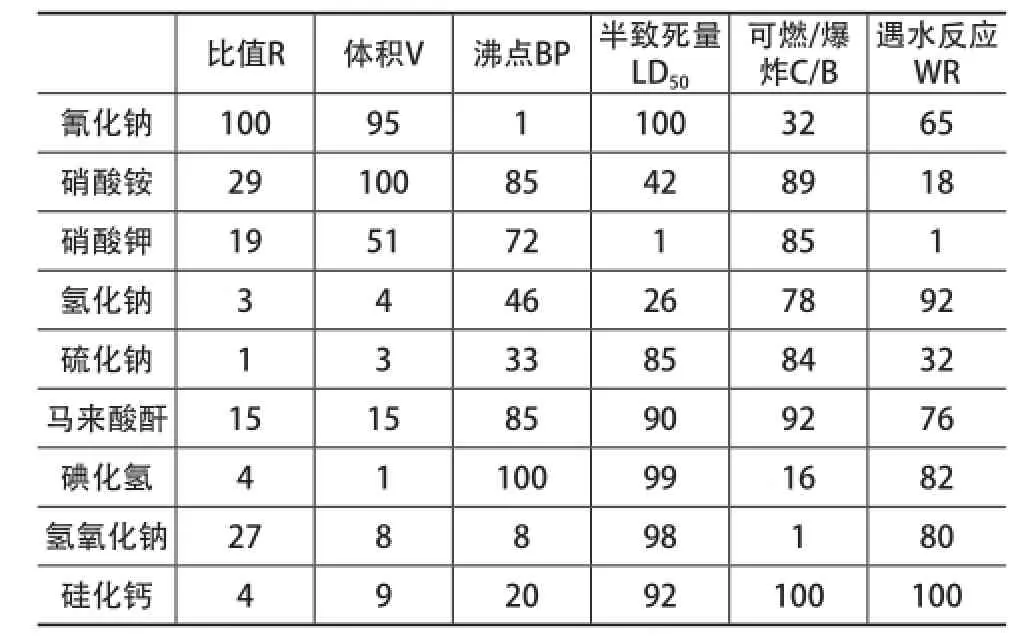
表3　危化品数据无量纲化统计表

根据危险物品储存量/临界值所求出的比值R，各物质R值，见表4。

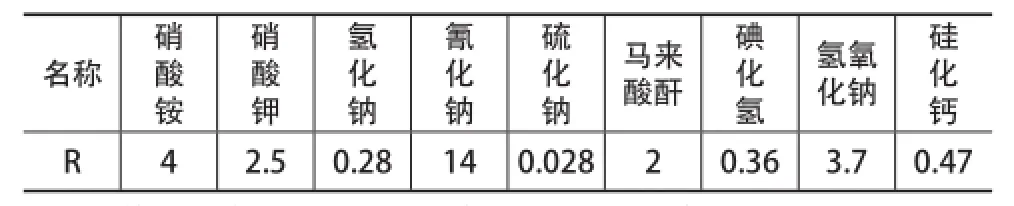
表4　储存物存的R值

若记其中的最大值氰化钠R值14为无量纲数100，最小值硫化钠R值0.028为无量纲数1，那么，利用插值法，得到硝酸钾比值的无量纲数为19。特别注意，无量纲数越大，就代表该物质的危险系数越大。在日常生活中，对其安全性要求就越高。线性插值公式

式中：

y—待求某数据无量纲数；

x—该数据实际值；

xmin—该组数据中最小值；

xmax—该组数据中最大值。

（3）确定分析的参考数据列依据灰色关联分析法寻找每个指标数据无量纲化之后的最大值，作为分析的参考数列，如下：

（5）求最值。由灰色关联分析法计算每个危化品无量纲化后各指标数据中的最值。

表5　无量纲数据差的绝对值计算表

（6）计算关联系数ζi（k）。依据计算关联系数的公式：

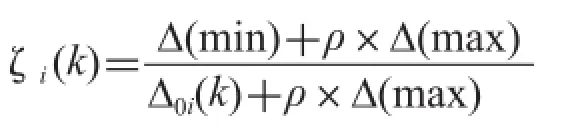
分别计算每个比较数列与参考数列对应元素的关联系数，其中分辨系数ρ取0.5［7］。计算的关联系数统计表，见表6。

表6　关联系数ζi（k）统计表

2.3应用层次分析法进行分析

依据层次分析法，对各指标之间进行两两对比之后，然后按9分位比率排定各评价指标的相对优劣顺序［9-10］，依次构造出评价指标的判断矩阵A为：

对判断矩阵A进行一致性检验。应用MATLAB计算出其特征值，见表7。

表7　判断矩阵A的特征值

由表7可知，最大特征值λmax为6.1249。计算得到CI为0.02498，再查表1得RI为1.26，因而矩阵A的一致性比率CR=0.0198＜0.1。说明矩阵A具有满意的一致性。

按照“和积法”求得A的列规范化矩阵为

表8　评价指标权重值

由以上统计的各危化品关联系数ζi（k）及其所对应的指标权重系数，计算危化品关联系数统计，见表9。

表9　危化品关联系数加权算术平均值统计表

在考虑各项指标之间的权重关系的前提下，从上面的关联系数表，可以清晰地知道，各物质的危险程度大小关系，依次为：氰化钠，硅化钙，马来酸酐，硝酸铵，氢碘酸，氢氧化钠，硫化钠，硝酸钾，氢化钠［8］。

3　结论

（1）利用灰色关联分析法分析仓库危化品，采用加权平均数计算法计算危化品的危险系数，不仅可以了解该危化品仓库各种危化品的储存量均高于储存的临界值，仓库已经属于重大危险源，还可以知道各种危化品的危险系数顺序为，氰化钠＞硅化钙＞马来酸酐＞硝酸铵＞氢碘酸＞氢氧化钠＞硫化钠＞硝酸钾＞氢化钠。

（2）分析中涉及到的危化品物理化学性质（如碘化氢气体遇水生成强酸；硅化钙遇水生成可燃气体，进而遇氧气发生爆炸；马来酸酐遇水容易水解生成具有腐蚀特性的顺丁烯二酸物质等），也使得作业人员在应对仓库突发火灾时，能采取正确地应对措施，避免了以往的由于作业人员对于危化品知识的欠缺，仓库在发生火灾时，单一的或者错误的使用自来水进行灭火而造成的人员生命、财产的更大灾难损伤的状况。依上可知，运用灰色关联分析法比以往的直接利用重大危险源分析法分析危化品更据有说服力，且分析结果也更加得准确和全面。

［1］ 国家安全生产监督管理总局.GB18218-2009，危险化学品重大危险源辨识［S］.北京：中国标准出版社，2009

［2］ 王佩，张定华，陈冰，等.基于模糊综合评价与灰色关联分析法的多工艺方案评价［J］.北京：航空动力学报，2012， （9）：2075-2085

［3］ 姚红.基于灰色关联分析法的期刊综合评价［J］.长春：情报科学，2003，（07）：730-734

［4］ 孙芳芳.浅议灰色关联度分析方法及其应用［J］.山东：科技信息，2010，（6）：880-882

［5］ 林鹏程，吴启勋.灰色关联度分析及应用［J］.西宁：盐湖研究，2001，（6）：48-50

［6］ 雷芳.危险化学品安全评价指导体系的研究［J］.武汉：中国地质大学工程学院，2004.5：8-16

［7］ 刘玥，薛喜成，何勇.灰色关联分析法在突然重金属污染评价中的应用［J］.武汉：安全与环境工程，2009，（01）：15-17

［8］ 姚桂莹，赵东风，赵朝成.大气环境质量评价的加权灰色关联分析法［J］，北京：油气田环境保护，2006，（04）：39-41

［9］ 刘宏.综合评价中指标权重确定方法的研究［J］.河北：河北工业大学学报，1996，（04）：75-80

［10］ 邓雪等.层次分析法权重计算方法分析及其应用研究［J］.北京：数学的实践与认识，2012，（4）：93-100

［11］ 洪志国，李焱，范植华，等.层次分析法中高阶平均随机一致性指标（RI）的计算［J］.计算机工程与应用，2002，（12）：45-47+150