P-P与P-SV波联合反演方法分类与对比

张远银,孙赞东,金之钧

(1.中国石油化工股份有限公司石油勘探开发研究院,北京100083;2.页岩油气富集机理与有效开发国家重点实验室,北京100083;3.国家能源页岩油研发中心,北京100083;4.中国石油化工股份有限公司页岩油气勘探开发重点实验室,北京100083;5.中国石油大学(北京),北京102249)



P-P与P-SV波联合反演方法分类与对比

张远银1,2,3,4,5,孙赞东5,金之钧1,2,3,4

(1.中国石油化工股份有限公司石油勘探开发研究院,北京100083;2.页岩油气富集机理与有效开发国家重点实验室,北京100083;3.国家能源页岩油研发中心,北京100083;4.中国石油化工股份有限公司页岩油气勘探开发重点实验室,北京100083;5.中国石油大学(北京),北京102249)

多波资料解释结果不仅取决于联合标定与资料匹配,而且取决于多波联合反演方法。依据实现原理的不同,将P-P与P-SV波联合反演方法分为叠后联合、属性间接联合、两参数直接联合和三参数直接联合四类,利用数值模型定量对比了单一P-P波反演方法和三类叠前P-P与P-SV波联合反演方法的差别。研究结果表明:①弹性参数直接联合反演方法的精度高于单一P-P波反演方法;②AVO属性间接联合反演的精度低于弹性参数直接联合反演;③噪声严重时,考虑到弹性参数相关性的属性间接联合、两参数直接联合反演方法可以在弹性参数相关性较好的情况下获得更加稳定的密度反演结果。

多波勘探;联合反演;属性反演;弹性参数

多波多分量资料中丰富的纵横波运动学(走时、速度、结构、相似性等)与动力学(振幅、频率、相位、吸收、衰减、频散、方位各向异性等)特征[1]可以联合用于储层非均质性和各向异性描述,从而最大限度地降低地质问题地球物理解的非唯一性,更好地解决复杂岩性和隐蔽油气藏勘探难题。P-P波与P-SV波联合反演方法虽然没有得到广泛应用,但已取得了相对长足的进步:1990年,卡尔加里大学CREWES研究小组创始人STEWART利用Gardner公式扩展了SMITH等[2]提出的P-P波反射系数加权叠加近似方法,建立了P-P与P-SV波联合反演方程[3],并带领研究团队开展了多项联合反演方法与应用研究;1999年,LARSEN进一步研究了同时反演纵波波阻抗和横波波阻抗的联合反演方法[4];2003年,ZHANG等对Pikes Peak油田的实际数据进行了联合反演应用[5];2004年和2006年,MAHMOUDIAN等[6]和VEIRE等[7]分别利用奇异值分解手段和最小二乘方法实现了联合方程下的三参数反演,并给出了在实际数据中的对比应用结果;2006年,VEIRE等在三参数联合反演过程中加入一个与资料信噪比有关的权系数,进一步提高了反演精度[7]。2004年,孙鹏远提出了基于P-P与P-SV波属性的联合反演思路[8];黄中玉等通过数值模拟证实了联合反演方法的可行性[9]。2009年,付雷等在松辽盆地北部开展了联合反演方法的实际应用研究[10]。2010年,张春涛等通过Aki的纵横波反射近似公式联合消元建立了两参数联合反演方程,避免了纵波与密度相关性不强造成的误差[11-12]。2014年,侯栋甲等建立了基于贝叶斯理论的多波联合反演方法[13]。

不同的联合反演方法原理不同,对于实际资料的适用性也不一样,但目前鲜有文献开展相关分类与定量对比研究。我们首先将现有的P-P与P-SV波联合反演方法进行整理分类,然后利用数值模型开展了不同类型反演方法的定量对比研究。

1　P-P与P-SV联合反演方法分类

P-P波与P-SV波联合反演方法经过多年的发展,依据其原理和实现方法的不同可以分为叠后

P-P与P-SV波联合反演、基于AVO属性的P-P与P-SV波间接联合反演、两参数P-P与P-SV波直接联合反演、三参数P-P与P-SV波直接联合反演4种。

1.1叠后P-P与P-SV波联合反演

纵横波叠后联合反演即先采用纵波和横波全叠加资料分别反演纵、横波阻抗,再计算其它岩石物理参数[1]。该方法虽然实现简单,但是反演的精度与纵横波剖面的标定和匹配密切相关,且最终不能获得密度参数。由于AVO效应的影响,全叠加纵波资料即便完全保幅也并非纯纵波资料,据此进行叠后反演的结果必然存在误差[14-15]。另外,由于P波垂直入射时不能产生S波反射,因而用全叠加横波数据进行叠后反演的做法缺乏理论依据。

1.2基于AVO属性的P-P与P-SV波间接联合反演

基于AVO属性的联合反演方法[8]是先依据P-P和P-SV波资料进行AVO属性反演,再通过获得的属性组合求取弹性参数。基于SHUEY的P-P波反射系数近似公式[16]和郑晓东等给出的P-SV波反射系数近似公式[17],可联立如下方程:

(1)

式中:A1=(Δα/α+Δρ/ρ)/2,B1=Δα/(2α)-(2β2/α2)Δρ/ρ-(4β2/α2)Δβ/β,C1=Δα/(2α),A2=-(2β/α)Δβ/β-(1/2+β/α)Δρ/ρ,B2=(2β2/α2+β/α)Δβ/β+[3β2/(4α2)+β/(2α)]Δρ/ρ,C2=(β4/α4)Δβ/β+[β4/(4α4)]Δρ/ρ;Δα=α2-α1,α=(α2+α1)/2,Δβ=β2-β1,β=(β2+β1)/2,Δρ=ρ2-ρ1,ρ=(ρ2+ρ1)/2,σ1=[1/2-(β1/α1)2]/[1-(β1/α1)2],σ2=[1/2-(β2/α2)2]/[1-(β2/α2)2],θ=(i1+i2)/2;α1,β1,ρ1和α2,β2,ρ2分别为界面两侧纵、横波速度及介质密度;i1和i2分别为P波入射和透射角度。

对于地下某一反射点,令纵波与转换横波地震共反射点道集数据分别为SPP(θ)和SPS(θ),对应的地震子波分别为WP(θ)和WS(θ),则可建立相应的P-P和P-SV波反演公式,即以下公式的解:

(2a)

(2b)

实际地震资料的入射角度往往不大,因而P-SV近似公式第3项C2sin2θ一般都非常小,所以常常采用前两项近似进行分析,P-P与P-SV数据的角度范围可以不一样。

当纵横波速度比约等于2时,A1,B1,A2本身为病态方程,稳定的属性组合有A1,B1,B2和B1,A1,B2两种[8],可得弹性参数分别如下:

(3a)

公式(3a)和公式(3b)获得的最终弹性参数通常基本相同。

1.3两参数P-P与P-SV波直接联合反演

在速度与密度的三参数近似形式下,由于P-P反射系数中有纵波速度、横波速度和密度三个参量,P-SV方程中只有横波速度和密度两个参量,因而狭义联合反演需要进行消元或增元以使其匹配。两参数反演的主要思路则是通过数学关系将三个参量简化为两项,由于纵波与横波信息对地下岩性和物性具有较高的分辨能力,且在实际资料角度范围内相比密度更加稳定,故常常成为两参数联合反演的目标参量。STEWART[3]在SMITH等[2]加权叠加方法的基础上,采用Gardner公式消除了密度项,建立以下联立方程,用以求解Δα/α和Δβ/β:

(4a)

式中:A=(1-4β2/α2sin2θ+4/cos2θ)/8,B=4β2/

α2sin2θ,C=-αtanj/β(1-2β2/α2sin2θ+2β/αcosθ·cosj),D=αtanj/(2β)(4β2/α2sin2θ-4β/αcosθ·cosj);j=(j1+j2)/2,j1和j2分别为P波入射时反射横波与透射横波的反射和透射角。

类似地,LARSEN等[18]和MARGRAVE等[19]建立了与阻抗相关的两项联合公式:

(4b)

式中:A=(1+tan2θ)/2,B=-4β2/α2sin2θ,C=-αtanj/(10β)(1+2sin2j-2β/αcosθcosj),D=αtanj/β(2sin2j-2β/αcosθcosj),ΔI/I=Δα/α+Δρ/ρ,ΔJ/J=Δβ/β+Δρ/ρ。

对于地下某一反射点,令纵波与转换横波共反射点道集数据分别为SPP(θ)和SPS(θ),对应的地震子波分别为WP(θ)和WS(θ),则可分别建立P-P和P-SV波两项反演公式:

(5)

求解公式(5)获得ΔI/I和ΔJ/J后,利用纵波阻抗与密度的关系可进一步获得Δα/α,Δβ/β和Δρ/ρ。

公式(4a)和公式(4b)利用纵波速度与密度之间的关系(Gardner公式)将问题简化,在二者相关性较差的区域必然存在误差。实际上,可以通过数学关系不做近似予以消元[11-12]。公式(4b)在引入Gardner公式消元前的形式为:

(6)

式中:A=(1+tan2θ)/2,B=-4β2/α2sin2θ,C=2β2/α2sin2θ-tan2θ/2,D=-αtanj/(2β)(1+2sin2j-2β/αcosθcosj),E=αtanj/(2β)(4sin2j-4β/αcosθcosj)。显然,利用Δρ/ρ=RPS/D-(E/D)ΔJ/J可以进一步求得RPP-CRPS/D=AΔI/I+(B-CE/D)ΔJ/J,从而建立数学消元后的联合方程。实际反演过程中,该方法只需要求解:

(7)

但是该方法要求P-P与P-SV波资料角度关系一致,在一定程度上限制了反演的能力。

1.4三参数P-P与P-SV波直接联合反演

两参数联合反演消去了密度项建立的反演方程,不能直接反演出密度,其转换获得的密度在纵波速度与密度相关性较差时必然存在误差。为此,MAHMOUDIAN等提出了基于奇异值分解的纵横波阻抗与密度反演方法,且通过模型与实际资料对比证实了该方法的优势[6]。其基本原理是直接从公式(6)出发,求解广义联合反演方程下的最小值问题:

(8)

VEIRE等在此基础上引入与资料信噪比有关的权系数重新定义目标函数[7]:

(9)

式中:w为取值范围在0～1的权系数,用以优选P-P与P-SV波资料,提高反演精度。(8)式和(9)式不要求P-P与P-SV波资料角度关系一致。

与上述广义三参数联合反演方法不同,HAMPSON等充分利用纵波与横波阻抗关系(lnZS=klnZP+kC+ΔLS)、纵波阻抗与密度关系(lnZD=mlnZP+mC+ΔLD)建立了三参数联合反演方程[20]:

(10)

(11)

2　不同反演方法反演结果对比

基于不同联合反演方法的原理,设计一个二维砂泥互层数值模型,用于定量对比P-P波反演、属性联合反演、两参数和三参数联合反演等四种典型反演方法在不同信噪比条件下的反演结果。反演的实现过程均依据基于柯西约束的贝叶斯原理,以提高反演的抗噪能力。

2.1模型参数

图1为设计的二维砂泥互层地质模型,仿照了我国渤海湾盆地西部凹陷沙河街组碎屑岩储层沉积模式,包括多套碎屑浊流砂泥互层沉积,整体为由西向东逐渐下降的构造趋势。该模型纵向包含151个采样点,采样间隔为2ms,横向上包括101道。首先通过Zoeppritz方程计算该地质模型在入射角分别为5°,15°和25°时的P-P与P-SV反射系数序列,然后选择主频为30Hz的雷克子波分别正演形成三个角度在无噪与含噪(S/N=1)时的道集记录,用于不同反演方法对比分析。

2.2反演结果对比

图2至图7分别对比了单一P-P波反演方法和3种P-P与P-SV联合反演方法在不同信噪比情况下获得的纵波梯度ΔI/I,横波梯度ΔJ/J和密度梯度Δρ/ρ。进一步提取模型中部CDP55处的纵波梯度ΔI/I,横波梯度ΔJ/J和密度梯度Δρ/ρ理论值以及各种反演结果与误差(图8)。图8中背景红线为理论值。无噪情况下部分反演方法误差曲线重合,如无噪声情况下单一P-P波反演和三参数联合反演的纵波梯度ΔI/I(图8a),单一P-P波反演、属性联合和三参数联合反演的横波梯度ΔJ/J(图8c),以及单一P-P波反演和三参数联合反演的密度梯度Δρ/ρ(图8e)等。

从图8可以看出,设计模型的密度梯度Δρ/ρ范围[-0.06,0.06]最小,仅为纵波梯度ΔI/I范围[-0.3,0.3]的1/5,而横波梯度ΔJ/J的范围最大,为[-0.4,0.4]。显然,不同的反演方法对不同的弹性参数有着不同的刻画精度;随着资料噪声的增加,反演结果的质量也会有不同程度的降低。

2.2.1单一P-P波反演

单一P-P波反演为公式(6)的纵波部分,在无噪情况下,单一P-P波反演结果非常精确,仅存在所用反演公式本身相对于Zoeppritz公式的近似误差。特别地,由于密度梯度Δρ/ρ对叠前纵波反射系数的贡献十分微小[14-15],其近似误差相对最大(图6c)。随着噪声强度的增加,单一P-P波反演质量急剧下降,相比而言,纵波梯度ΔI/I表现出最强的抗噪性(图3c,图8b),横波梯度ΔJ/J次之(图5c,图8d),密度梯度Δρ/ρ抗噪性最差(图7c,图8f)。

2.2.2属性联合反演

依据P-P和P-SV波资料分别进行叠前反演,利用所得结果构建最终反演参数的属性联合反演方法(公式(2)与公式(3a))采用的是间接手段,包含了多个计算步骤,存在一定的累计误差。尽管同

时利用了P-P和P-SV波资料,但即便是在没有噪声的情况下,属性联合反演的纵波梯度ΔI/I(图2e,图8a)仍然存在比横波梯度(图4e,图8c)与密度(图6e,图8e)梯度更大的误差,这是因为这种方法在构建弹性参数时假设纵横波速度比为常数,而纵波梯度对纵横波速度比的依赖程度最强(公式(3a)或者(3b)),所以最终的累计误差最大。该方法对横波梯度和密度梯度的反演误差则相对较小。

2.2.3两参数联合反演

两参数联合反演方法,即公式(4b)与公式(5),采用Gardner公式及纵波与密度的近似关系消除了密度项,因而即使在没有噪声的情况下也存在近似误差,其中密度梯度Δρ/ρ最为明显(图6g,图8e)。但是,由于该方法同时直接利用了纵波和转换横波资料求取弹性参数,反演的纵波梯度ΔI/I(图3g,图8b)、横波梯度ΔJ/J(图5g,图8d)均表现出最强的抗噪能力。特别地,得益于纵波参量在反演过程中较强的稳定性和抗噪性,通过纵波计算的密度梯度Δρ/ρ(图7g,图8f)在低信噪比情况下也相对比较准确。

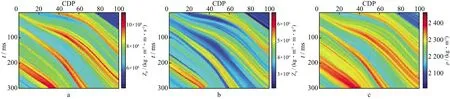
图1　二维砂泥互层地质模型a 纵波阻抗模型; b 横波阻抗模型; c 密度模型

图2　无噪声情况下4种反演方法获得的ΔI/I及相应误差对比a 理论值; b,c P-P波反演结果与误差; d,e 属性联合反演结果与误差; f,g 两参数联合反演结果与误差; h,i 三参数联合反演结果与误差

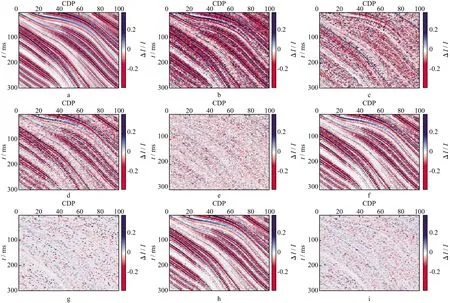
图3　含噪声(S/N=1)情况下4种反演方法获得的ΔI/I及相应误差对比a 理论值; b,c P-P波反演结果与误差; d,e 属性联合反演结果与误差; f,g 两参数联合反演结果与误差; h,i 三参数联合反演结果与误差

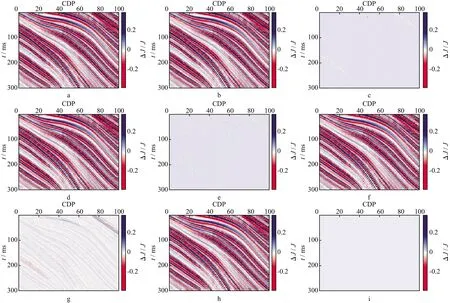
图4　无噪声情况下4种反演方法获得的ΔJ/J及相应误差对比a 理论值; b,c P-P波反演结果与误差; d,e 属性联合反演结果与误差; f,g 两参数联合反演结果与误差; h,i 三参数联合反演结果与误差

图5　含噪声(S/N=1)情况下4种反演方法获得的ΔJ/J及相应误差对比a 理论值; b,c P-P波反演结果与误差; d,e 属性联合反演结果与误差; f,g 两参数联合反演结果与误差; h,i 三参数联合反演结果与误差

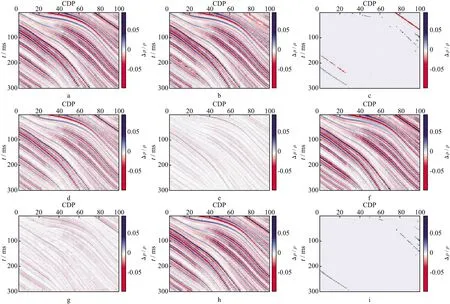
图6　无噪声情况下4种反演方法获得的Δρ/ρ及相应误差对比a 理论值; b,c P-P波反演结果与误差; d,e 属性联合反演结果与误差; f,g 两参数联合反演结果与误差; h,i 三参数联合反演结果与误差

图7　含噪声(S/N=1)情况下4种反演方法获得的Δρ/ρ及相应误差对比a 理论值; b,c P-P波反演结果与误差; d,e 属性联合反演结果与误差; f,g 两参数联合反演结果与误差; h,i 三参数联合反演结果与误差

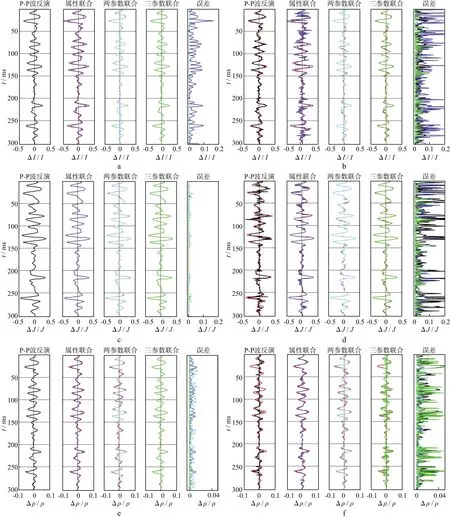
图8　CDP55处4种反演方法获得的ΔI/I(a,b),ΔJ/J(c,d),Δρ/ρ(e,f)及相应误差对比(背景红线为理论值; a,c,e为无噪情况;b,d,f为含噪情况)

2.2.4三参数联合反演

三参数联合反演方法即公式(6)与公式(8),同样同时直接利用了纵波和转换横波信息,且对纵波和转换横波反射系数的近似程度最小,因而其在无噪声情况下获得的各种弹性参量(图2i,图8a,图4i,图8c,图6i,图8e)最准确。虽然在CDP55处三参数联合反演和单一P-P波反演的密度梯度相同(图8a),但从图6i和图6c可以看出,前者反演精度更高。

当资料信噪比降低时,三参数联合反演方法反演的纵波梯度ΔI/I(图3i,图8b)、横波梯度ΔJ/J(图5i,图8d)均表现出很强的抗噪能力,其精度与两参数联合反演结果相近,但是,密度梯度Δρ/ρ的反演精度却显著降低(图7i,图8f),不及两参数联合反演(图7g,图8f)和属性联合反演(图7e,图8f)结果,仅优于单一P-P波反演的结果(图7c,图8f)。

一般密度梯度本身的数值变化范围很小,仅为纵波和横波梯度的几分之一,且在叠前反射系数中的贡献最小(公式(6)中的密度梯度系数C在入射角较小的情况下常常约等于0),因而在同等低信噪比资料条件下,其反演精度远不及纵波和横波梯度[14-15]。正因为如此,实际密度反演过程中常常利用其与纵波的关系加上正则化约束来构建稳定的反演方程,获得更加可靠的反演结果。所以,在同等低信噪比的资料条件下,三参数联合反演方法由于利用了转换横波资料,可以比单一P-P波反演方法获得更加准确的密度梯度结果(图7h与图7b,图8f对比)。而属性联合反演方法由于首先采用纵波和转换波资料分别获得与纵波和横波梯度密切相关的各种弹性参数,然后间接构建密度梯度,降低了噪声对密度梯度的影响,因此相当于利用纵波、横波与密度之间的隐形关系提高了密度梯度的反演精度(图7e,图8f)。两参数联合反演方法直接采用Gardner公式基于纵波速度与密度的近似关系消除了密度项,相当于在反演过程中直接对密度梯度施加了正则化约束条件,所以在低信噪比情况下获得了较为准确的密度反演结果(图7g,图8f)。综上所述,实际含噪声资料条件下,施加正则化约束条件的三参数联合反演方法最易于准确获得各种弹性参数。

除了反演方法,实际情况下不同的地质条件和资料品质都会影响最终的反演结果。本文中测试的误差百分比反映了同一地质和特有资料条件下不同反演方法的误差,在实际应用中可能会有数值上的差别,但同等条件下应有相似的趋势,因为这些误差本质上源于不同反演方法自身原理的近似或假设。

3　结论

1) 同等资料品质下,P-P与P-SV波直接联合反演方法的反演精度高于单一P-P波反演;

2) 即便没有噪声,P-P与P-SV波属性间接联合反演的纵波梯度仍然存在误差;

3) 噪声严重时,考虑了弹性参数相关性的P-P与P-SV波属性间接联合反演、两参数直接联合反演方法可以在弹性参数相关性较好的情况下获得更加稳定的密度反演结果;

4) 实际最理想的联合反演方法为施加了约束条件的三参数联合反演。

[1]唐建明.转换波三维三分量地震勘探方法技术研究[D].成都:成都理工大学,2009

TANG J M.Methods and technologies study on converted-wave 3D-3C seismic exploration [D].Chendu:Chengdu University of Technology,2009

[2]SMITH G C,GIDLOW P M.Weighted stacking for rock property estimation and detection of gas[J].Geophysical Prospecting,1987,35(9):993-1014

[3]STEWART R.Joint P and P-SV inversion [R].Calgary:The CREWES Project Research Report,1990:112-115

[4]LARSEN J A.AVO inversion by simultaneous PP and PS inversion[D].Calgary:University of Calgary,1999

[5]ZHANG H,MARGRAVE G F.Joint PP-PS inversion at Pikes Peak oilfield,Saskatchewan[R].Calgary:CREWES Research Report,2003:1-12

[6]MAHMOUDIAN F,MARGRAVE G F.Three parameter AVO inversion with PP and PS data using offset binning[J].Expanded Abstract of 74thAnnual Internat SEG Mtg,2004:721-724

[7]VEIRE H H,LANDRO M.Simultaneous inversion of PP and PS seismic data[J].Geophysics,2006,71(3):R1-R10

[8]孙鹏远.多属性AVO分析及弹性参数反演方法研究[D].吉林:吉林大学,2004

SUN P Y.Studies on the method of multi-attribute AVO analysis and elastic parameters inversion [D].Jilin:Jilin University,2004

[9]黄中玉,赵金州.纵波和转换波AVO联合反演技术[J].石油物探,2004,43(4):319-322

HUANG Z Y,ZHAO J Z.Simultaneous P- and S-wave AVO inversion [J].Geophysical Prospecting for Petroleum,2004,43(4):319-322

[10]付雷,王建民,许红,等.纵波和转换波联合反演技术在松辽盆地北部LMD地区的应用[J].石油物探,2009,48(6):563-567

FU L,WANG J M,XU H,et al.Simultaneous P- and S-wave AVO inversion and its application in LMD area,northern Songliao Basin [J].Geophysical Prospecting for Petroleum,2009,48(6):563-567

[11]张春涛,王尚旭,李生杰,等.纵横波联合反演方法研究及应用[J].石油地球物理勘探,2010,45(4):520-524

ZHANG C T,WANG S X,LI S J,et al.Compressional and shear wave joint inversion technique research and its application [J].Oil Geophysical Prospecting,2010,45(4):520-524

[12]张春涛,王尚旭.PP波和PS波联合反演方法研究进展[J].科技导报,2010,28(10):106-110

ZHANG C T,WANG S X.Review of joint inversion of PP and PS waves[J].Review of Science and Technology,2010,28(10):106-110

[13]侯栋甲,刘洋,任志明,等.基于贝叶斯理论的VTI介质多波叠前联合反演[J].石油物探,2014,53(3):294-303

HOU D J,LIU Y,REN Z M,et al.Multi-wave prestack joint inversion in VTI media based on Bayesian theory [J].Geophysical Prospecting for Petroleum,2014,53(3):294-303

[14]ZHANG Y Y,SUN Z D,FAN C Y.An iterative AVO workflow for S-wave improvement[R].75thEAGE Annual Meeting,2013

[15]SUN Z D,ZHANG Y Y,FAN C Y.An iterative AVO inversion workflow for pure P-wave computaiton and S-wave improvement[J].The First Break,2014,32(10):23-26

[16]SHUEY R T.A simplification of the Zoeppritz equations[J].Geophysics,1985,50(4):609-614

[17]郑晓东.Zoeppritz方程的近似及其应用[J].石油地球物理勘探,1991,26(2):129-144

ZHENG X D.The approximation and application of Zoeppritz equation [J].Oil Geophysical Prospecting,1991,26(2):129-144

[18]LARSEN J,MARGRAVE G,LU H X.AVO analysis by simultaneous P-P and P-S weighted stacking applied to 3C-3D seismic data[J].Expanded Abstract of 69thAnnual Internat SEG Mtg,1999:721-724

[19]MARGRAVE G F,STEWART R,LARSEN J A.Joint PP and PS seismic inversion[J].The Leading Edge,2001,20(9):978-982

[20]HAMPSON D P,RUSSELL B H.Simultaneous inversion of pre-stack seismic data[J].Expanded Abstract of 75thAnnual Internat SEG Mtg,2005:1633-1637

(编辑：戴春秋)

Classification and quantitative comparison of P-P and P-SV wave joint inversion methods

ZHANG Yuanyin1,2,3,4,5,SUN Zandong5,JIN Zhijun1,2,3,4

(1.SinopecExplorationandProductionResearchInstitute,Beijing100083,China; 2.NationalKeyLaboratoryofShaleOil/GasEnrichmentMechanismandEffectiveDevelopment,Beijing100083,China; 3.NationalEnergyR&DCenterofShaleOil,Beijing100083,China; 4.SinopecKeyLaboratoryofShaleOil/GasExplorationandProductionTechnology,Beijing100083,China; 5.ChinaUniversityofPetroleum,Beijing102249,China)

The interpretation of multi-components seismic data is not only dominated by the integrated calibration and matching degree of P-P and P-SV wave data,but also affected by the effectiveness of corresponding P-P and P-SV wave joint inversion.In this paper,all the published P-P and P-SV joint inversion methods are classified into four types.Subsequently,a set of 2D numerical data is adopted to test the effectiveness of conventional P-P wave inversion and three types of prestack P-P and P-SV wave joint inversion.It is revealed that the inversion results of direct elastic parameters joint inversion are more accurate than that of the conventional P-P wave inversion.Moreover,the indirect attributes joint inversion is inferior to direct elastic parameters joint inversion.Particularly,the indirect attribute and direct two-term joint inversion could produce more steady density results in a noisy environment if the inversion parameters have good correlations.

multiwave exploration,joint inversion,attributes inversion,elastic parameter

2015-12-07;改回日期：2016-02-17。

张远银(1986—),男,博士,主要从事地震数据叠前反演研究。

国家重点基础研究发展计划(973计划)项目(2014CB239104)和国家科技重大专项(2016ZX05049002)联合资助。

P631

A

1000-1441(2016)04-0587-10DOI:10.3969/j.issn.1000-1441.2016.04.014

This research is financially supported by the National Key Basic Research and Development Program of China (973 Program) (Grant No.2014CB239104) and the National Science and Technology Major Project of China (Grant No.2016ZX05049002).