土坡各参数对土坡稳定性的影响研究

任宇涛，李素娟

（1．中国恩菲工程技术有限公司，北京100038；2．北京中冶设备研究设计总院有限公司，北京100029）

土坡各参数对土坡稳定性的影响研究

任宇涛1，李素娟2

（1．中国恩菲工程技术有限公司，北京100038；2．北京中冶设备研究设计总院有限公司，北京100029）

建立了边坡稳定性分析的平面直角坐标系，得到了该坐标系下的边坡稳定分析瑞典圆弧法的积分表达式。以简单均质黏性土坡为研究对象，结合Matlab遗传算法工具箱，建立了基于瑞典圆弧法的遗传算法优化模型，实现了边坡稳定分析最小安全系数的自动寻优。通过实例进行验证和对比，表明该方法是行之有效的，经大量实例计算，得到了土坡参数对土坡安全系数Fs、滑移体断面面积A、滑移体周长L的影响的规律。

土坡稳定；积分法；遗传算法；影响规律

0 引言

边坡失稳是人类经常遇到的自然地质灾害之一，给人类带来了巨大的经济损失和人员伤亡，受到了全世界的广泛关注。因此，对边坡的正确认识，合理的设计，适当的治理，把边坡失稳造成的灾害降到最低程度，是岩土工程界的学者和工程设计人员所面临的重要岩土工程问题。

为此，本文建立了基于瑞典圆弧法土坡稳定分析数值积分法；用遗传算法作为计算工具，并用Matlab编制了相应计算程序，实现了边坡稳定分析最小安全系数的自动寻优，经大量实例计算分析统计，得到了土坡各参数对土坡稳定性的影响规律。

1 土坡稳定安全系数积分表达式的推导

设有简单均质土坡AODC，坡面OD为单纯的直线斜坡，坡高为h，坡比i＝1∶m，土的容重为γ，黏聚力为c，内摩擦角为φ。建立平面直角坐标系，坐标原点取在坡脚处，如图1所示。

设土坡滑动时，滑动面ABC为圆弧面，其圆心坐标为O （x0，y0），半径为R。如图1所示，假设滑弧与坡底平面和坡顶平面分别相交于A点和C点，则土坡的边界方程为

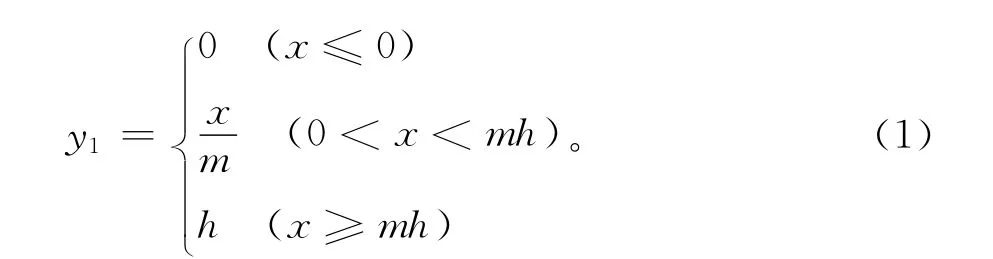
滑动圆弧方程为

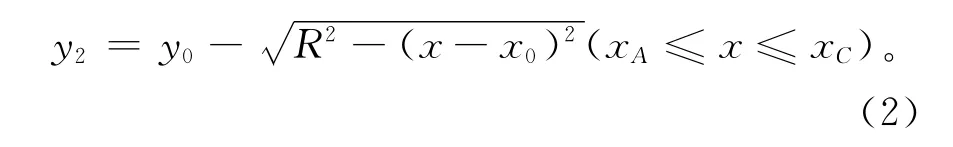
其中

图1 边坡稳定分析坐标系及微分土条受力分析

从滑动土体内取出任一单位厚度的微分土条，土条宽度为dx，作用在该微分土条上的诸力如图1所示。图中dw表示微分土条的重量，易见dw≈（y1－y2）dx；dN表示作用在微分土条底面的法向力；dS表示微分土条底面引发的抗剪力；E表示作用在微分土条上的侧向水平推力；dE表示作用在微分土条上侧向水平推力增量；X表示作用在微分土条侧面上的竖向剪力；dX表示作用在微分土条侧面上的竖向剪力增量；a为径向线与过圆心的铅垂线之间的夹角；dα为角的增量；dl为滑弧微分弧段的弧长，显然dl＝Rdα。从图中可看出：

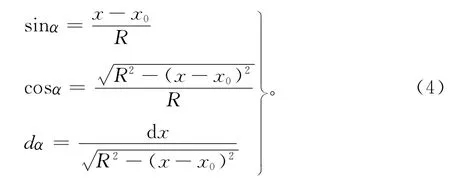
本文采用瑞典圆弧法的土坡稳定安全系数定义［1］，则对简单均质土坡有

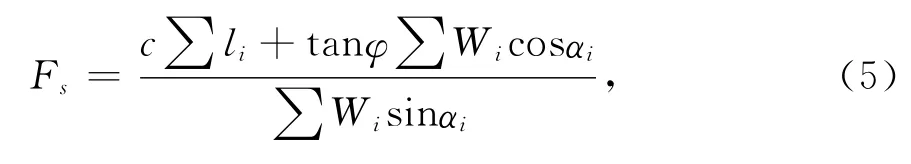
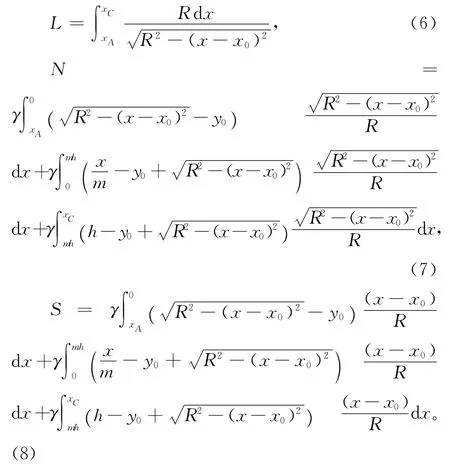
当滑动面为坡面圆时，坡面方程与滑弧方程表达式均不变，只是滑弧与坡面的左交点坐标有所变化，即

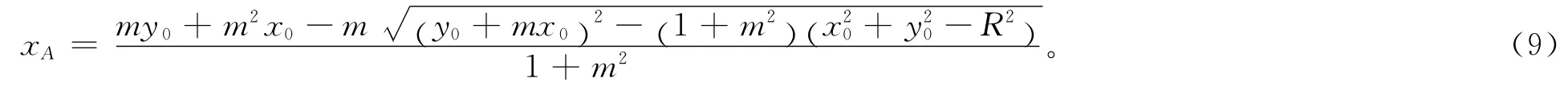
则边坡稳定安全系数表达式中的L，N和S的积分表达式为：

在给定的积分区间内，可得到式（5）～（12）的封闭解，即可得到边坡稳定安全系数Fs的数值解。

2 遗传算法优化模型的建立

遗传算法［2］（Genetic Algorithm，简称GA），由美国holand教授提出，现已经被广泛地应用于许多领域。是一种公认的全局搜索能力强、搜索效率高的算法。该法仿效生物的遗传和进化，从某一初始群体出发，根据达尔文进化论中的“生存竞争”和“优胜劣汰”的原则，借助复制、杂交、变异等操作，不断迭代计算，经过若干代的演化后，群体中的最优值逐步逼近最优解。克服了传统方法容易陷入局部极小值的缺点，尤其适用于传统最优化方法难以解决的全局极大或极小和多参数的非线性问题［3］，从而成为一种在边坡稳定性分析中值得推广的确定最危险滑动面及其对应的最小安全系数的方法。

边坡稳定性分析的目的是在所有可能的滑移面中找出安全系数最小的滑弧，即最危险的滑移面。因此，可选取边坡稳定安全系数公式作为目标函数，也即是遗传算法优化数学模型的适应度函数。根据上述推导，可建立设计变量x0、y0和R与稳定安全系数Fs之间的函数关系。则边坡的稳定性分析可表示为如下的优化模型问题：

式中fitnessfun为遗传算法的目标函数，也是遗传算法的适应度函数为变量x0，y0和R的取值范围。

在使用遗传算法工具时，将目标函数和参数编写成扩展名为．m的M文件，并把编制好的此M文件保存到Matlab路径的工作目录下。这个M文件可以接受一个行向量，并且返回一个标量，行向量的长度就是目标函数中独立变量的个数，返回的标量即为优化的最终结果［4］。

3 算例验证

本文引用文献［5］中第20页边坡实例进行分析计算。该均质土坡，坡高h为50m，土体容重γ为19．62kN／m3，土的黏聚力c为58．86kPa，内摩擦角φ为11．3°，坡比i＝1∶3．25。其最小稳定安全系数Fs＝1．276745。若在本文建立的坐标系中进行分析，最危险滑弧圆心坐标x0＝59．21m，y0＝134．715m，半径R＝152．125m。采用本文遗传算法优化模型经过50代进化演算后所得，该土坡最小稳定安全系数Fs＝1．273 945，可见，和张天宝瑞典积分法计算结果相比，本文所提方法计算结果正确，因坐标系选取不同以及小数点截断误差造成二者在小数点后第3位出现偏差，但在工程应用中足以满足。本文所采用的遗传算法进化过程如图2所示。横坐标表示遗传进化的代数，纵坐标表示适应度值。图中上方的“×”代表每一代中的平均适应度值，下方的“◆”代表每一代的最佳适应度值。由图2可看出，算法在开始时每代适应度值的变化较明显，在进化到第24代的时候已经接近最优解，此后开始逐步逼近最优解。算法在第50代停止，停止原因是50代为本文规定的遗传算法运行的最大代数。

图2 遗传算法进化过程示意图

运用本文所提出的遗传算法优化模型，计算给定土坡，当其他参数一定，某一参数变化对土坡的稳定安全系数Fs、滑移体断面面积A、滑移体周长L的影响，得出了变化规律：1）安全系数Fs与黏聚力几乎成直线关系增长，滑移体断面面积A与黏聚力成对数关系；2）安全系数Fs与内摩擦角基本上成指数关系，滑移体断面面积A与黏聚力成对数关系增长；3）安全系数Fs、滑移体断面面积A与重度均负线性关联；4）安全系数Fs与坡比成直线关系增长，而滑移体断面面积A与坡比成二次函数关系增长。见表1～4所示。

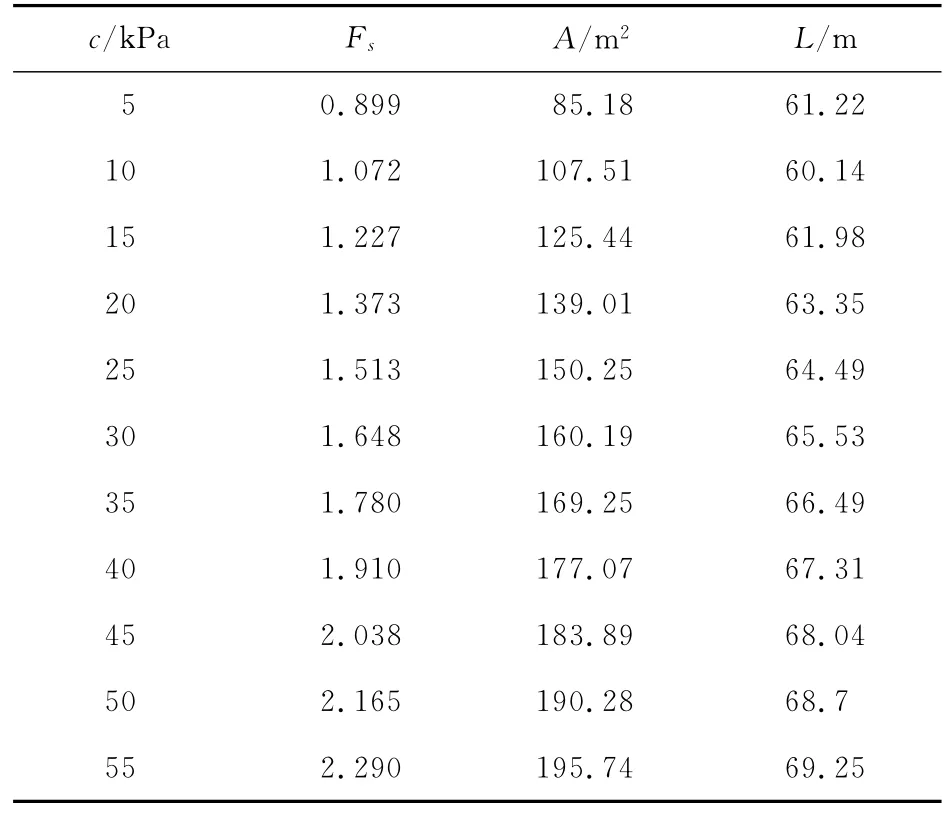
表1 安全系数、滑移体断面面积、滑移体周长与黏聚力c的关系

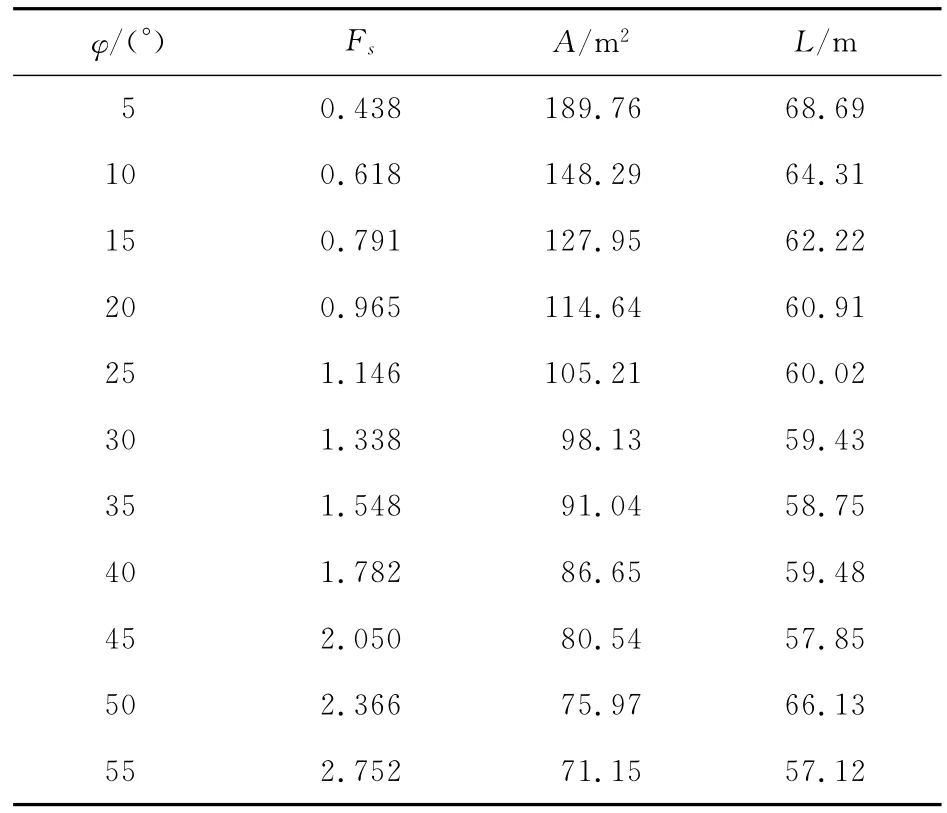
表2 安全系数、滑移体断面面积、滑移体周长与内摩擦角φ的关系

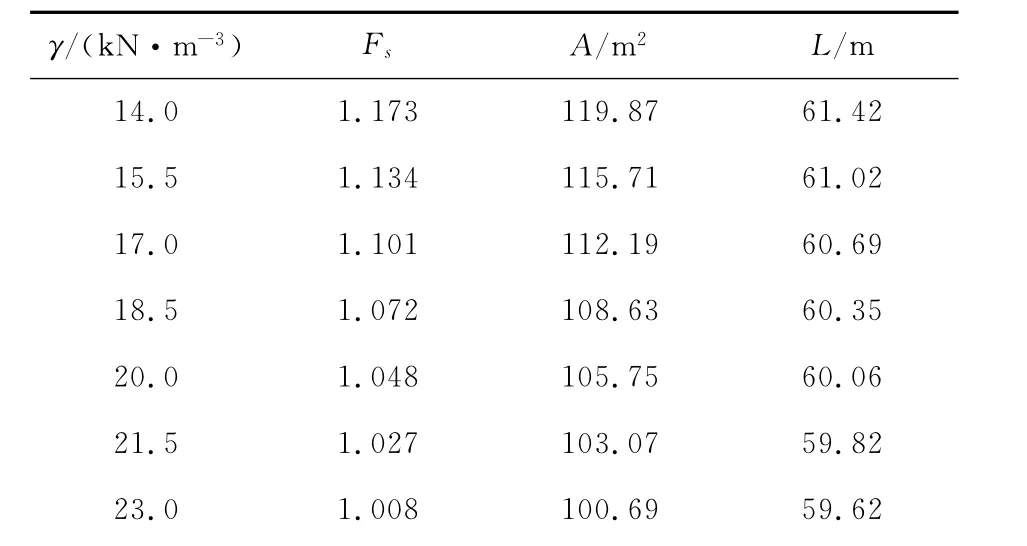
表3 安全系数、滑移体断面面积、滑移体周长与重度γ的关系

24．5 0．991 98．78 59．46 26．0 0．976 96．36 59．20 27．5 0．962 94．14 59．16 29．0 0．950 92．75 58．90

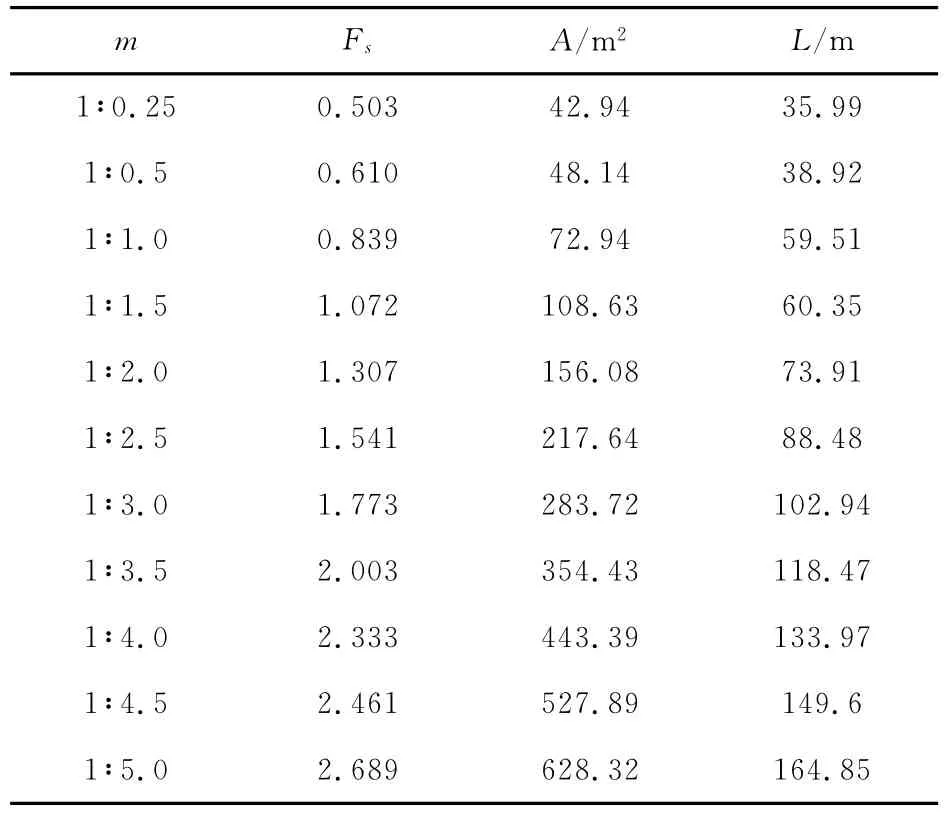
表4 安全系数、滑移体断面面积、滑移体周长随坡比m的关系

由表1～4可知：1）随着黏聚力c的增大，土坡稳定安全系数Fs是有所提高，但其滑移体断面面积增加明显，故在边坡支护设计中不能因土体的黏聚力c提高而缩短土钉墙支护结构的钉长。2）随着内摩擦角φ的增大，土坡稳定安全系数Fs提高明显，滑移体断面面积减小明显，故在边坡治理工程中宜尽可能采用提高内摩擦角的办法。3）随着土体重度γ的增大，土坡稳定安全系数Fs滑移体断面面积均有所降低，但幅度不大。4）随着坡比m的增大，土坡稳定安全系数Fs提高明显，但其滑移体断面面积也增加明显，在边坡设计中应合理确定坡比m。

5 结语

1）建立了文中所述平面直角坐标系，提出了基于瑞典圆弧法原理的土坡稳定分析数值积分法。由基本力学概念可知，此方法与传统条分法相比，计算精度不受土条划分粗糙程度的影响，其计算结果更趋合理。

2）建立基于遗传算法的边坡稳定性分析优化模型，并用Matlab编制程序实现了边坡稳定分析最小安全系数的自动寻优，得出边坡最小稳定安全系数Fs、滑移体断面面积A、滑移体周长L。

3）通过算例计算与对比得出：本文提出的基于遗传算法的土坡稳定性分析瑞典法的数值解是一种很好的全局优化算法，能够很好地搜索到全局最优解——最危险滑裂面。

4）通过大量计算分析得到了土坡各参数对土坡稳定安全系数Fs、滑移体断面面积A、滑移体周长L的影响规律，为土坡设计提供一定的参考。

［1］钱家欢，殷宗泽．土工原理与计算［M］．北京：中国水利水电出版社，1996。

［2］John H．Holand，Adaptation in natural and artificial systems［M］．second edition．Cambridge，MA：MIT press，1992．

［3］李敏强，寇纪淞．遗传算法的基本理论与应用［M］．北京：科学出版社，2002．

［4］雷英杰，张善文．Matlab遗传算法工具箱及应用［M］．西安：西安电子科技大学出版社，2005．

［5］张天宝．土坡稳定分析和土工建筑物的边坡设计［M］．成都：成都科技大学出版社，1987．

［6］李素娟．基于遗传算法的边坡稳定性分析研究［D］．西安：西安建筑科技大学，2008．

The Study on the Influence of Soil Slop Parameters to Soil Slopes Stability

REN Yu－tao，etc．
（China Enfi Engineering Co．，Ltd．，Beijing100038，China）

A plane right－angle coordinates for the stability of soil slopes analysis is set up．And the integral expression of the stability analysis based on the Sweden arc method has been obtained under this coordinates．The research object in this paper is simple homogeneous clay slope．A genetic algorithm optimization model based on the Swedish arc method has been established by combining with Matlab Genetic Algorithm Toolbox．It can realize automatic optimization to the minimum safety factor during slope stability analysis．An example is given and compared with other methods，which indicates that this method is effective and feasible．After the calculation to a great deal of instances，a lot of information have been received，such as the safety factor Fs to soil slope，slip body cross－sectional area A，the impact law to sliding body circumference L．

soil slop stability；integral method；genetic algorithms；effect rule

TU432

A

1009－8984（2016）02－0014－04

10．3969／j．issn．1009－8984．2016．02．004

2016－05－24

任宇涛（1982－），男（汉），陕西，硕士主要研究边坡工程治理及工业与民用建筑设计。