截面受损条件下钢框架结构的动力稳定性研究

张曙光，张红霞

（1．长春工程学院土木工程学院；2．吉林省土木工程抗震减灾重点实验室，长春130012）

截面受损条件下钢框架结构的动力稳定性研究

张曙光1，2，张红霞1

（1．长春工程学院土木工程学院；2．吉林省土木工程抗震减灾重点实验室，长春130012）

对钢框架结构在截面受损情况下进行动力稳定性分析，建立截面不同受损伤状态下的钢框架有限元分析模型，分析在不同幅值的地震波作用下结构的最大水平位移。根据第二类动力稳定性理论，得出结构发生动力失稳时的临界地震荷载，并与未受损情况比较，得出底层柱腹板、翼缘处受损将使结构更容易发生动力失稳的结论。

钢框架结构；动力稳定性；损伤

0 引言

钢结构的动力稳定性问题有两类判定准则［5］。第一类稳定是基于Lyapunov运动稳定性定义与线弹性稳定相对应的特征值屈曲分析；第二类稳定则是基于极值理论与双重非线性增量分析相对应的稳定极限承载力分析。前者本质上是弹性动力屈曲问题，后者本质上是动力极值的问题，根据B－R失稳准则，结合动态增量法进行研究。本文利用第二类动力稳定性准则建立钢框架结构的动力稳定性时程分析。

1 动力稳定性判别准则

1．1 第一类动力稳定

钢框架结构在动荷载作用下会产生内力和变形，不同的几何构型与结构应力场对应不同的稳定性临界荷载和失稳模式。

在地震动过程中，对时程中每一时刻的结构状态进行冻结，作为前屈曲状态，仿照静力第一类失稳的方法建立其t时刻的动力失稳特征方程（1），从而获得动力响应全过程对应的屈曲特征值曲线，以此判断在整个地震动过程中动力屈曲是否会发生。

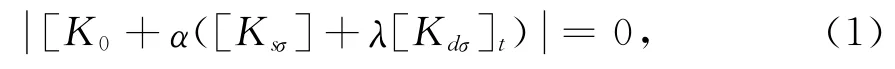
式中：K0为结构的初始弹性刚度矩阵；α为动力屈曲系数；Ksσ为恒载引起的轴力对刚度矩阵所起的作用；λ为输入地震波的比例系数；Kdσ为t时刻动轴力对结构刚度矩阵的影响。

1．2 第二类动力稳定性

第二类动力稳定，是参照B－R准则的动力稳定性判别方法，当荷载幅值的微小增量导致结构特征响应发生很大变化时，结构视为动力失稳。此时所对应的荷载即结构响应的动力稳定性临界荷载。

运用动态增量法IDA（incremental dynamic analysis）可以实现该动力稳定的求解。动态增量法是用于评估地震动作用下结构性能参数化分析的方法。将地震动的加速度乘以一系列加速度调整系数，使之成为一组强度不同的地震动，各自进行非线性动力时程分析。

对比两类动力稳定分析发现：第一类是弹性动力稳定性分析，结构的刚度仅与荷载和结构的几何形状有关。而第二类是动力极限承载力问题，考虑了结构的初始缺陷、几何非线性以及材料非线性，从而得出临界荷载，其结果更符合实际情况。

2 非线性时程分析法

大多数土木工程结构的动力响应，会在结构或者全部构件超过屈服极限时发生非线性变形。此时，结构构件所受到的作用力和相应的变形之间将呈现非线性关系，求解需要运用迭代法。

多自由度体系的运动方程为：

振动过程中，式（2）在时刻tj＋1和tj的形式为

和

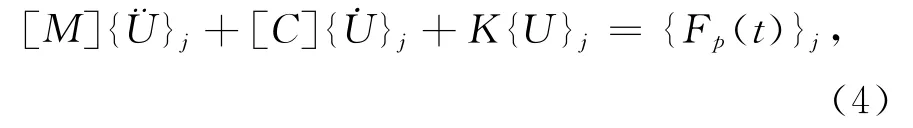
两式相减，得增量方程

式中：［M］为结构质量矩阵；［C］为结构阻尼矩阵；［K］为结构刚度矩阵；｛U｝、｛ U｝、｛¨U｝为位移、速度、加速度向量；｛Fp（t）｝为动荷载向量。

式（5）的求解采用直接积分法，其基本思想：1）对时间离散时，不要求任何时刻都满足运动方程，而仅要求在离散点上满足运动方程。2）直接积分法的计算过程是：假设t＝0时刻的状态（位移、时间及加速度）是已知的，将时间求解域0≤t≤T进行离散，即可有已知t＝0时刻的状态向量计算t＝0＋Δt时刻的状态向量，进而计算t＝t＋Δt时刻的状态向量，直至t＝T时刻终止，这样便可以得到动力响应的全过程。

直接积分的计算方法有很多，各方法在数学上的收敛性和稳定性均不同，计算精度也不同。

Newmark法是在线性加速法的基础上进行修改，线性加速度法假定质点的加速度反应在任意微小的时段Δt内呈线性关系，如图1所示。

图1 Δt时刻的加速度变化

在Δt＝tj＋1－tj内，结构的加速度反应是关于时间τ的线性函数，即取

可以将方程式（5）化为关于｛ΔU｝的线性代数方程，从而可以方便解答问题。为此，首先将位移｛U｝按泰勒级数在tj附近展开

对τ进行求导，得

当τ＝Δt时，显然有｛U（tj＋τ）｝＝｛U｝j＋1，而式（7）、式（8）可改写为

Newmark法是将式（9）、式（10）改写为

将式（6）代入式（11）、式（12）得Newmark方程：

HHT方法对Newmark方法引入α参数进行修正，得到

式中α参数取值为－1／3～0，以确保积分方程的收敛。

本文运用Hilber－Hughes－Taylor（HHT）方法，是Newmark方法的修正。

3 结构截面损伤后的动力稳定性有限元分析

3．1 模型建立

运用有限元软件建立一个6层钢框架模型如图2所示，长宽：6 000mm×6 000mm，底层层高为5 400mm，其余各层层高为3 900mm，建筑总高度为24．9m。采用Q235工字型钢作为梁柱用钢。楼板采用C30的混凝土，其中钢筋选用HPB300，厚120mm。

本模型的建立是按抗震设防烈度为7度、基本风压为0．65kN／m2、地面粗糙程度为B类的地区。考虑结构自重、梁上线荷载9kN／m、板上面荷载2kN／m2、水平风荷载、E－L地震时程波。

根据不同的截面损伤建立4种工况下的有限元分析模型。

图2 钢框架模型

3．2 梁柱构件截面参数

不同工况下的截面参数见表1。

表1 不同工况的截面参数

3．3 地震波的选取

本文选用E－L波，其峰值加速度为304．8cm／s2，在荷载工况中输入比例系数，使得A＝220cm／s2，并输入1．1A、1．2A以及各个幅值的加速度地震波。输入的时程波曲线如图3所示。以关键部位时间历程中位移最大的柱顶节点作为特征响应的控制点来进行分析。

图3 E－L地震波

3．4 结果分析

3．4．1 工况1

由SAP2000动力计算可得到对应各个幅值地震波作用下的位移时程，从而得到地震波幅值与最大位移的关系曲线和发生最大位移的时刻。地震波峰值与最大位移绝对值的关系曲线如图4所示。

图4 最大位移—地震波峰值曲线

由图4可看出，在地震波峰值达到3．9A之前最大位移随着地震波峰值增大而增大，有一定的规律，而在地震波峰值达到3．9A之后，将峰值再增加0．1A时，最大位移突然从0．412 7m增大到1．005m，由动力稳定性第二定律，当荷载幅值的微小增量导致结构特征响应发生很大变化时，结构视为动力失稳，由此得出3．9A是该结构的极限地震载荷，即该结构的极限地震加速度为858cm／s2。

图5是地震波幅值为3．9A时结构控制点的位移时程曲线，在5．48s时，位移最大达到0．412 7m，最后仍在某一位置有规律的上下摆动。图6是地震波幅值为4A时结构控制点的位移时程，在19．4s时，位移达到最大值1．005m，呈现发散状态，脱离了原来的平衡位置，结构在此时发生动力失稳。

图5 3．9A时结构控制点的位移时程曲线

图6 4A时结构控制点的位移时程曲线

3．4．2 工况2

地震波峰值与最大位移绝对值的关系曲线如图7所示。

图7 最大位移—地震波峰值曲线

由图8～9可以看出，在地震波峰值达到3．4A之前，结构顶点最大位移随地震波峰值增大而增大，有一定的规律，而在地震波峰值达到3．4A之后，将峰值再增加0．1A时，最大位移突然从0．354 7m增大到0．391 8m，由动力稳定性第二定律，得出3．4A是该结构的极限地震载荷，即该结构的极限地震加速度为748cm／s2。

图8 3．4A时结构控制点的位移时程曲线

工况2与无损状态相比，底层柱腹板损伤使结构在动荷载作用下的极限承载力降低12．82%。

图9 3．5A时结构控制点的位移时程曲线

3．4．3 工况3

地震波峰值与最大位移绝对值的关系曲线如图10所示。

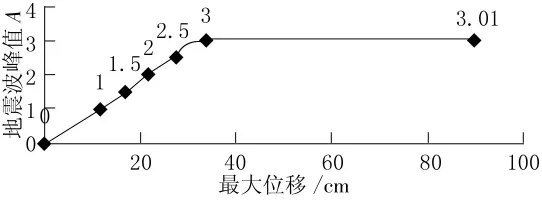
图10 最大位移—地震波峰值曲线

由图11～12可看出，在地震波峰值达到3A之前，结构顶点最大位移随地震波峰值增大而增大，有一定的规律，而在地震波峰值达到3A之后，将峰值再增加0．01A时，最大位移突然从0．334 8m增大到0．897 3m，由动力稳定性第二定律，得出3．4A是该结构的极限地震载荷，即该结构的极限地震加速度为660m／s2。

图11 3A时结构控制点的位移时程曲线

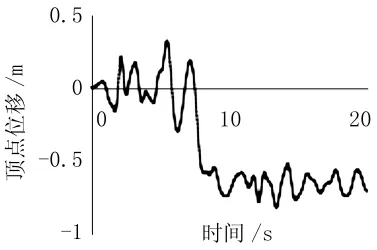
图12 3．01A时结构控制点的位移时程曲线

底层柱构件翼缘处的损伤使得结构在动荷载作用下的极限承载能力降低较大，较无损状态情况下降低23．07%。因此，当发现底层柱翼缘受到损伤时对结构的动力稳定性影响较大，必须加以重视。

3．4．4 工况4

地震波峰值与最大位移绝对值的关系曲线如图13所示。

图13 最大位移—地震波峰值曲线

由图14～15可以看出，在地震波峰值在2．9A之前，结构顶点最大位移随地震波峰值增大而增大，有一定的规律，而在地震波峰值达到3A之后，将峰值再增加0．1A时，最大位移突然从0．324 8m增大到0．875m，由动力稳定性第二定律得出2．9A是该结构的极限地震载荷，即该结构的极限地震加速度为638cm／s2。

图14 2．9A时结构控制点的位移时程曲线

图15 3A时结构控制点的位移时程曲线

工况4与无损状态相比底层梁柱翼缘均受损使结构在动荷载作用下的极限承载力降低25．64%；与工况3对比可知，底层梁翼缘处受损使结构所能承受的极限地震荷载影响不大，仅使其减小2．57%。

4 结语

通过减小截面面积模拟结构构件的损伤，建立6层钢框架进行模态分析和动力时程分析，对比4种工况下结构所能承受的极限地震荷载，可以看出：1）工况2与无损状态相比底层柱腹板损伤使结构在动荷载作用下的极限承载力降低12．82%。2）工况3为底层柱构件翼缘处的损伤，结构在动荷载作用下的极限承载能力降低较大，较无损状态情况下降低23．07%。因此，当发现底层柱翼缘受到损伤时对结构的动力稳定性影响较大，必须加以重视。3）工况4与无损状态相比，底层梁柱翼缘均受损使结构在动荷载作用下的极限承载力降低25．64%。4）工况4与工况3对比可知，底层梁翼缘处受损对结构所能承受的极限地震荷载影响不大，仅比工况3减小2．57%。结构柱翼缘、腹板受损对框架结构承受的极限地震荷载影响较大。

［1］陈晓艳．强震作用下考虑损伤累积的钢结构稳定性分析［D］．南京：南京林业大学，2013．

［2］段红霞．钢结构地震损伤分析与损伤识别方法研究［D］．大连：大连理工大学，2010．

［3］Chopra A K，Goel R K．A modal pushover analysis procedure for estimating seismic demands for buildings［J］．Earthquake Engineering and Structural dynamics，2012，31：561－582．

［4］袁继胜．钢结构加工和安装偏差对结构性能影响［D］．郑州：郑州大学，2010．

［5］王述超，张行，叶志雄，等．超限高层建筑地震作用下的动力稳定性分析［J］．振动与冲击，2009，28（4）：149－152．

［6］Li Zhongxue，Shen Zuyna，Deng Changgen．Nolinear Dynamic Stability of Farmes under Earthqukae Loading［M］．Shanghai：InternationalConference on Nonlinear Meehnaies，2011：287－291．

［7］董可．地震作用下钢框架结构的动力性状研究［D］．北京：中国矿业大学，2013．

［8］周晓慧．基于ANSYS的钢框架结构地震作用分析研究［D］．石家庄：河北工程大学，2014．

The Analysis to Dynamic Stability of Steel Frame Structure with Sectional Damage

ZHANG Shu－guang，etc．
（School of Civil Engineering，Changchun Institute of Technology，Changchun130012，China）

This article makes an analysis to the dynamic stability of steel frame structure in section damage case，establishes different cross－section steel frame damage model，and analyzes structure horizontal dis－placements under the action of seismic wave with different amplitudes．According to the second class of dynamic stability theory，critical seismic load when structure is in dynamic instability has been derived．This is compared with the undamaged case to draw the conclusion that the dynamic instability of structures easily happen in damaged bottom column web，and damaged flange structure．

steel frame structure；dynamic stability；damage

TU311．3

A

1009－8984（2016）02－0001－05

10．3969／j．issn．1009－8984．2016．02．001

2016－04－21

吉林省自然科学基金项目（20130101050JC）

张曙光（1968－），女（汉），吉林白山，教授，博士主要研究结构优化设计。