混杂纤维轻骨料混凝土配合比优选研究

陈晓梅

（长春工程学院土木工程学院，长春130012）

混杂纤维轻骨料混凝土配合比优选研究

陈晓梅

（长春工程学院土木工程学院，长春130012）

随着轻骨料混凝土的广泛应用，对其性能进行综合评价凸显出必要性。主成分分析法是通过降维的过程，在保证原始数据信息损失最小的条件下，用较少的综合变量代替原有多维变量对混凝土的综合性能进行评价。试验选取了聚丙烯纤维、木质素纤维和粉煤灰为变量，并选取轻骨料混凝土的其他5项主要测试指标，采用主成分分析法对这些指标进行数值处理，得出了评价轻骨料混凝土综合性能的数学模型。

主成分分析法；轻骨料混凝土；数学模型

浮石，又名轻石或浮岩，因其孔隙率大、质量轻、容重小且能浮于水面而得名。我国浮石资源丰富，分布广泛，北方地区较多。将其作为粗骨料加入混凝土中可减轻混凝土的自重，改善混凝土自重大的缺点。目前，轻骨料混凝土的应用越来越广泛，影响其性能的因素很多，然而这些因素的影响程度不同。为了能够快速准确地寻求混杂纤维轻骨料混凝土的最佳性能，可以利用数学方法建立混杂纤维轻骨料混凝土的力学性能及其影响因素之间的数学关系，从而探索其最优配合比［1－2］。主成分分析法在对高维变量降维与简化的过程中，可以最大限度地保留原始数据的基本信息，客观地确定各指标的权重，避免主观随意性［3］。基于此，运用主成分分析法建立一个评价混杂纤维轻骨料混凝土的综合模型，对试验样本进行优化，为其配合比设计提供理论依据。

1 主成分分析的基本原理

主成分分析是通过对高维变量进行降维，把众多与混凝土性能相关联的因素转化为几个不相关的综合因素的一种统计方法，即通过转化后可以用较少的几个因素来取代并综合反映原有较多的复杂信息，这些转化后的综合因素就是原有众多复杂因素的主要成分［4］。主成分分析降维的目的主要有：1）是可以通过较少的几个潜在因素分析原有众多影响因素的相关性；2）分类处理众多影响因素，经处理后的几个影响因素能够用来表达尽可能多的信息量［5］。基于主成分分析法的这两个优点，将混凝土性能评价集中到所选出的几个因素上来，由此可以通过混凝土性能的优劣来选出其最佳的配合比。

1．1 主成分分析的数学模型

假设从n个样本中，测得p项（p＜n）指标，则原始数据资料阵就可以表示为：X＝（X1，X2，…，Xp）。如果将协差阵表示为Σ，则令λ1≥λ2≥…≥λp为Σ的特征根，所以有Var（F1）≥Var（F2）≥…Var（Fp）≥0，向量l1，l2，…，lp为相应的单位特征向量，则X的第i个主成分为

通常，可以用样本协差阵S来代替未知的协差阵Σ。同时，为消除各项指标量纲不同带来的影响，需要将原始数据进行标准化［6］，即：

得出相关阵后，便可得到特征值进而做主成分分析。从理论上来讲，全部变量都可以被作为主成分而提取出来，然而这样做就失去了该方法简化数据的意义。通常来说，当前k个主成分（通常为前2～3个主成分）的累计贡献率已能够表达90%以上的信息时，我们将人为地忽略其他成分［6］。

1．2 主成分分析的步骤

1）为消除数量或者量纲对变量的影响，首先将原来的p个指标进行标准化，

2）根据标准化后的数据矩阵求出协方差或相关阵

式中rij（i，j＝1，2，……，p）为原来变量ri和rj的相关系数，rij＝rji，其计算式为

3）求出协方差矩阵的特征根和特征向量。通过对R的特征方程进行求解，可以得到p个特征值λi（i＝1，2，…，p），并且这些特征值均是非负的，由大到小的顺序排列为：λ1≥λ2≥…λp≥0。求得的特征向量为αi（i＝1，2，…，p），且其中αij是向量αi的第j个分量。

4）主成分贡献率及累计贡献率。得到特征根和特征向量后，需要分别对主成分贡献率μi和主成分Fi的累计贡献率υF，i进行计算，如下所示：

根据累计贡献率值的大小来提取主成分，通常，能够表达混凝土综合性能的主成分的累计贡献率需要达到一个较高值（如85%）［7］。

5）主成分载荷δij的计算

6）样本的综合得分。经过前5步的计算，混杂纤维轻骨料混凝土的综合性能便可以得到，进而得到最优组以寻找最佳配合比。

2 轻骨料混凝土试验样本模型的建立

试验着重研究了聚丙烯纤维、木质素纤维和粉煤灰3个变量对轻骨料混凝土性能的影响。文中选取的试验样本基本能够全面反映掺纤维轻骨料混凝土信息指标的部分试验数据，见表1。

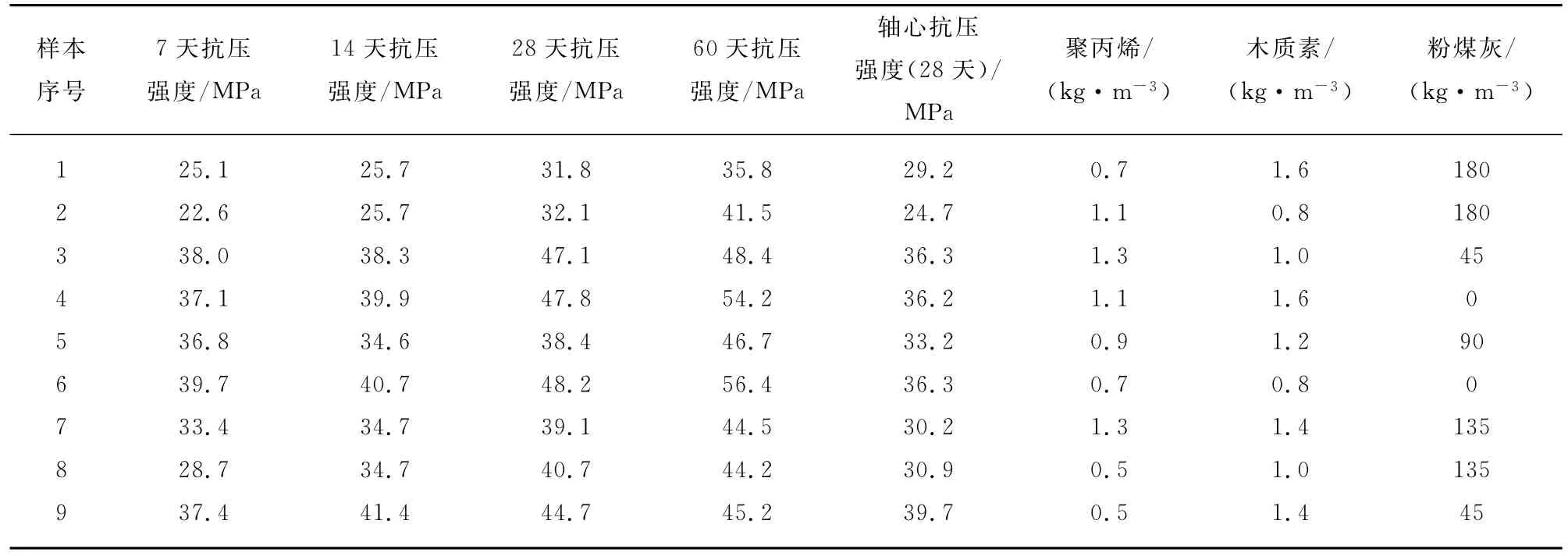
表1 轻骨料混凝土试验样本

2．1 KMO检验和Bartlett球形检验

利用SPSS软件对试验数据进行主成分分析时，必须忽略混凝土各指标量纲的影响，因此，在分析前需要对数据进行标准化处理。首先，要确定一组数是否能够采用主成分分析的方法，需要进行KMO检验与Bartlett球形检验。KMO检验是用于检查各个变量间的偏相关性，通常在实际分析中，KMO统计量在0．5以上时，主成分分析的效果比较好；Bartlett球形检验用于检查各变量间是否具有相关性，它建立在原有变量的相关系数矩阵上，检验假设的单位相关阵和实际的相关阵是否存在差异。如果两者之间的差异性是显著的，则可以表明变量之间存在显著的相关性，该组数据具备做主成分分析条件［6］。检验结果见表2。

表2 KMO检验与Bartlett球形检验

由表2结果可以看出，该组混凝土试验样本的K＞0．6，说明可以进行主成分分析。同时，又因为Sig＜0．05，再一次验证该试验样本做主成分分析是合理的。

2．2 共同度

公因子提取之后便可计算各个变量的共同度。变量的共同度表示各个变量所含有的原始信息能够被提取出的公因子表示的程度，变量的共同度见表3。由表中提取的共同度可知：所提取变量的共同度均大于80%，由此可知提取的公因子可以强有力地解释所有变量。

表3 变量的共同度

2．3 主成分的特征值和贡献率

计算混杂纤维轻骨料混凝土的8个影响因素的特征值和累计贡献率，计算结果见表4。

表4 影响因素特征值和累计贡献率

从表4中可以看出，前3个成分的累计贡献率已经达到了较高的水平92．976%，在所有影响混凝土的因素中的累计贡献率最大，因此，提取这3个成分作为所有影响因素的主成分，图1为8个影响因素的碎石图。从图中可以看出，用3个主成分来代替8个影响因素是合理的。

图1 碎石图

同时，由主成分因子载荷图（图2）和因子载荷矩阵（表5）可知，隶属于主成分F1的指标有7天抗压强度、14天抗压强度、28天抗压强度、60天抗压强度和粉煤灰，隶属于主成分F2的是木质素，隶属于主成分F3的是聚丙烯。从混凝土专业知识的角度来看，F1代表混凝土强度，F2和F3分别代表掺入混凝土的不同性质的纤维种类。

图2 主成分因子载荷图

表5 因子荷载矩阵

2．4 混杂纤维轻骨料混凝土综合性能指标的计算

各成分的得分系数计算结果见表6，并且各因子的权重均以其作为依据，由此得到混凝土的综合性能指标：

F1＝0．199X1＋0．192X2＋0．191X3＋0．105X4＋0．186 X5＋0．048 X6＋0．053 X7－0．193 X8，F2＝0．075 X1＋0．056 X2－0．056 X3＋0．189 X4－0．032 X5＋0．797 X6＋0．036 X7－0．374 X8，F3＝0．144X1－0．002X2＋0．091X3－0．175X4－0．147X5＋0．912X6－0．058X7－0．055X8。根据筛选出的可以反映混凝土综合性能的3个主成分，可以计算出各主成F1、F2和F3的权重，见表7所示，则可得出评价混凝土综合性能的表达式为

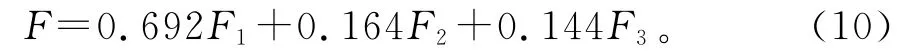
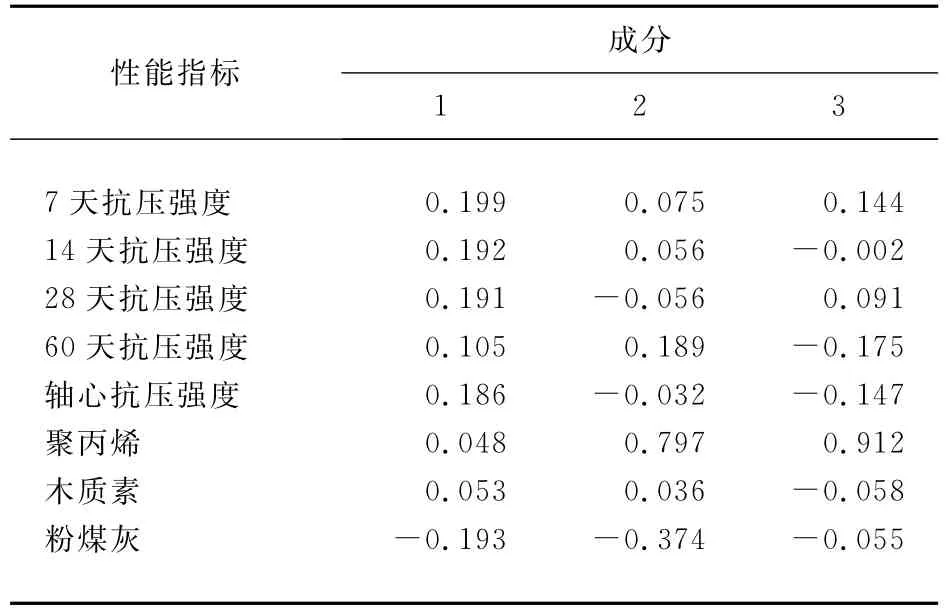
表6 各成分得分系数矩阵

表7 各主成分综合权重

2．5 轻骨料混凝土综合评价结果

借助Excel计算试验样本的综合评价结果，前3名排序结果见表8。由表可知，样本4的综合评价是最高的，可以考虑该组配合比作为最优配合比。由此可知，第4组的综合性能评价是最高的，可以确定为最优配合比。

表8 轻骨料混凝土试验样本综合评价结果

3 结语

1）主成分分析法通过对原有变量进行降维处理，提取出少数综合影响因素为混杂纤维轻骨料混凝土的综合性能评价提供一种快捷的方法。

2）由主成分分析及综合性能表达式可以得出：聚丙烯纤维对轻骨料混凝土综合性能的影响略强于木质素纤维的影响。

3）科学运用数理统计的方法，对试验样本进行合理的选取，通过建立的模型得到混杂纤维轻骨料混凝土的最佳性能，实现配合比的优化设计。

［1］安宁．高性能混凝土配方优化方法的研究［J］．混凝土，2006（9）：72－76．

［2］郑山锁，赵鹏，商效瑀．高强高性能混凝土配合比优化设计［J］．中国科技论文，2013（5）：413－416．

［3］潘怀兵．基于主成分分析法的沥青路面使用性能评价［J］．重庆交通大学学报：自然科学版，2010（6）：888－890．

［4］宇传华．SPSS与统计分析［M］．北京：电子工业出版社，2006．

［5］汪海东，曾志兴．基于主成分分析法的高性能再生混凝土性能优化设计［J］．混凝土，2011（4）：51－53．

［6］张文彤．SPSS统计分析高级教程［M］．北京：高等教育出版社，2004．

［7］王起才，鲍学英．基于主成分分析法的C50高性能混凝土配合比优选研究［J］．铁道建筑，2013（4）：152－155．

The Research on the Optimization to Mix Ratio of Hybrid fiber in Lightweight Aggregate Concrete

CHEN Xiao－mei
（School of Civil Engineering，Changchun Institute of Technology，Changchun130012，China）

With the wide application of lightweight aggregate concrete，the necessity to evaluate the perform－ance of each kind of concrete．The principal component analysis method is the process of dimension reduction，ensuring the condition of minimizing loss to original data information，using fewer variables to evaluate the performance of concrete instead of the original multidimensional variable．During the experiment，polypropylene fiber，lignin fiber and fly ash have been chosen as variables，and other five major indexes of lightweight aggregate concrete have been chosen．The numerical treatment has been made to these indicators by using the principal component analysis method．A mathematical model to evaluate the comprehensive performance of lightweight aggregate concrete has been gotten．

principal component analysis method；lightweight aggregate concrete；mathematical model

TU528

A

1009－8984（2016）02－0006－04

10．3969／j．issn．1009－8984．2016．02．002

2016－03－29

吉林省教育厅“十二五”科学技术研究项目（120150042）

陈晓梅（1981－），女（蒙古），长春，讲师，硕士主要研究道路与桥梁工程。