基于HLA的模型级仿真成员组合技术研究

朱国华，丁建军，杨　晨，代　扬

基于HLA的模型级仿真成员组合技术研究

朱国华，丁建军，杨晨，代扬

（江汉大学 数学与计算机学院，湖北 武汉430056）

基于高层体系结构（HLA）的仿真中通常以COM服务组件的形式对HLA接口进行封装，实现仿真模型的复用。随着仿真规模的进一步扩大，会产生联邦成员过多的问题，从而提高仿真成本。提出模型级别成员组合的概念，在基于COM的联邦仿真成员重用技术基础上，探讨采用有向图描述数据订购关系的相关理论问题，设计通用仿真成员依据有向图调度多个仿真模型，在不破坏成员之间数据传递关系的前提下，将多个仿真模型组合为一个联邦仿真成员，从而减少了仿真联邦成员的数量，降低了仿真的成本。

HLA仿真；联邦成员；模型组合；数据订购

HLA（High Level Architecture）仿真系统中最重要的资源是仿真模型［1］。模型组合的目的是最大限度地实现仿真模型的组合与重用，通过替换组件的方式实现仿真系统的结构和行为的发展演化。国内外己有的研究取得了不少成果［2］，但是目前模型描述复杂，建模过程繁琐，验模，最重要的缺陷是模型组合后，仿真联邦成员的数量过多。本文针对基于HLA的并行仿真系统设计了一个基于通用联邦成员［3］的组合建模的方法。该系统满足以下特征：针对控制系统建模，知识库设计难度相对较低；基于HLA仿真成员重用技术，模型的可重用性强；将多个仿真模型组合成为一个仿真联邦成员，减少联邦成员数量。

1　相关技术介绍

1.1HLA仿真中的成员重用技术

在基于HLA的仿真成员的重用技术［4］中，每个仿真联邦成员由三个组件构成：

（1）承担调度仿真责任可执行文件。该执行文件通过加载DLL（Dynamic Link Library）模型算法和读取成员模型描述XML（Extensible Markup Language）文件后形成一个联邦成员。

（2）模型关联描述文档。该文档描述了公布和订购的对象类和交互类，以及相关的成员的初始化参数等信息。

（3）若干DLL文件，主要实现了仿真实体的具体功能算法，被称为仿真模型。比如实现了联邦成员中的一个PID（Proportional⁃Integral⁃Derivative）控制器算法等。

1.2仿真模型的概念

仿真模型是一个仿真成员的核心功能。多个模型构成模型库为：

ML=｛M1，M2，…，Mn|n∈N｝

其中每一个模型：M=｛（I1，I2，…，Im，O1，O2，…，On，N1，N2，…，N）j|m∈N∧n∈Ν∧j∈Ν｝，对于任一个模型存在多个相关向量，包括输入参数I，输出参数O，初始参数N。

1.3仿真联邦成员之间的订购关系

并行仿真中发布/订购关系，对于对象类，从给定的联邦成员的角度来看是存在该对象类的已订购属性；对于交互类，该交互类是一个已订购交互类。

成员之间的订购关系，由于每个成员有不同的交互类和对象类公布，当另一成员发现自己需要的交互类和对象类，就会进行订购操作，即订购了其他成员的发布的对象类和交互类。这种订购可以是一对一的关系，也可以是一对多的关系。对于任何一个成员而言，成员之间存在的订购关系有两种：交互类订购关系和对象类订购关系。

1.4组合模型的两种途径

在基于HLA的仿真系统中，实现模型的组合有两种方式：

（1）成员级别的组合［5⁃6］：组合模型在用户层次见到的是一个成员，但是在底层实现依然是多个联邦成员，以某种关系组合而成。

（2）模型级别的组合：组合模型只生成一个实在的联邦成员，也就是说一个仿真成员底层是由多个仿真模型算法实现；多个算法模型DLL组合成一个联邦成员。

这两种方式各有优缺点。虽然在并行仿真系统中，模型与成员一对一的关系更符合并行仿真系统的调度方式，但是在实际仿真项目中，大多数投资者不愿意采用这种方式，原因是实际仿真项目中成员的数量成千上万，使得系统需要生成大量的仿真联邦成员，直接使运营成本提高。第二个方式，组合成员不仅能解决成员数量的问题，还能解决成员之间复杂的数据传递关系，即组合成员可以嵌套组合成员，存在的问题是可能产生代数环问题，使用时有特定的限制。

2　模型组合原理介绍

图（Graph）是图论的基本研究对象，表示物件与物件之间的关系。一个图由多个顶点或和连结这些顶点的线组成。

有向图是一个二元组＜V，E＞，其中：V是非空集合，称为顶点集；E是V×V的子集，称为弧集。直观来说，若图中的每条边都是有方向的，则称为有向图。有向图中的边是由两个顶点组成的有序对，有序对通常用尖括号表示，如＜vi，vj＞表示一条有向边，其中vi是边的始点，vj是边的终点。＜vi，vj＞和＜vj，vi＞代表两条不同的有向边。

完全有向图有n个顶点的有向图有n（n-1）条边，则此图称为完全有向图。从某个顶点出发经过若干条边回到该点的图是一个有向无环图DAG（Directed Acy⁃ cline Praph）。因为有向图中一个点经过两种路线到达另一个点未必形成环，因此有向无环图未必能转化成树，但任何有向树均为有向无环图。有向无环图的生成树个数等于入度非零的节点的入度积。

本系统将内部成员的订购关系，先转化为DAG，再进行拓扑排序，生成组合成员内部的DLL调度顺序。

2.1组合模型关系描述［7］

为了描述清楚，本文使用内部成员的概念来描述一个组合模型中的一个组成成分。但其在HLA仿真运行中，内部成员并不会作为一个联邦成员加入联邦，其只是组合成员内部的一个运行部分。同时组合模型的内部成员之间仍然存在和联邦成员之间同样的订购交互关系和互操作性［8］。

模型之间的关联信息表达为：

R=｛（Mref1，Mref2）|Mref1∈ML∧Mref2∈ML｝

其中可用关系集：RL=｛R1，R2，…，Rn｝，其中RL表示模型的内部成员需要满足的传递关系集合；NL=｛N1，N2，…，Nn｝，NL表示所有联邦成员之间能够满足的数据传递关系集合；A表示模型库中所有模型能够满足数据传输关系集合。则有关系A=RL∨NL。

组合模型定义如下：

CM=（｛M1，M2，…，Mm，A）|Mm∈ML∧Rn∈RL∧m，n∈N｝，其中ML已定义。

2.2规则与推论

对于任意两个模型M1与M2，可以形成如下关系：

Os=｛O1，O2，…，Om｝，O是模型M1的所有输出集合；

Is=｛I1，I2，…，In｝，I是模型M2的所有接收集合；

做笛卡尔积则对于所有产生的输入输出关系，有传输关系：

K =｛（o，i）|o∈O｝s，i∈Is

则对于任意两个模型，二者产生的关联关系为：

R=｛Os，Is，K｝

关系R可以映射成为有向图G。对于传输关系K，可以映射成为有向图＜V，E＞中的弧集E。对于输入输出集合Is和Os，可以映射成为有向图＜V，E＞中的顶点集V中的输入输出顶点。

2.3将订购关系建模成有向图

由于组合成员内部成员存在和普通成员一样的订购交互关系，这种关系可以简单的采用关系对来描述：假设D1，D2代表组合成员里的内部成员，如D2订购了D1的消息，可以记录这种关系为D1⁃D2，同理D3订购D1的消息，D4订购了D2，D3的消息即D1⁃D3，D2⁃D4，D3⁃D4，如图1所示。把这种关系理解为有向图里的顶点以及其前驱，于是可以把这种关系进行汇总，从而生成有向图。

图1　订购关系有向示意图

2.4组合模型调度原理介绍

先检查订购关系是否存在闭环；如果存在闭环需要先对闭环进行单独处理，打开有向环从而重构成为一个DAG。然后按照拓扑排序解AOE网（Activity on Edge Network）的过程求解组合成员之间的数据传递关系：

（1）在有向图中选一个没有前驱的顶点并输出；

（2）在图中删除该顶点和所有以它为尾的弧。

具体调度方法采用递归算法。在内部成员的描述文件中，记录了组合成员中的发布/订购关系，即数据传递顺序。取出一对关系，采用拆分的方法，分别存储为关系数组里的顶点及其前驱点，例如D1⁃D2，D1就加入第一个数组，D2加入第2个数组。然后调度函数对比两个数组，如果第1个数组中有元素第2个数组没有对应订购元素，则将这个元素加入第3个数组，在循环外遍历关系数组分别删除此元素和与其对应的元素，然后递归调用，直至关系数组为空。如果同一层的订购数组不止一个，就同时启动多线程调用多个DLL，以达到分组并行的目的。

图2　无环有向图（DAG）的调度策略

3　成员组合关系中有环有向图的处理

在处理组合成员数据传递关系时可能会遇到有环有向图的现象（控制系统中的闭环），此时就无法得到DAG。这是常规拓扑排序解决不了的问题，需要先对有向环进行单独处理。

有环有向图处理流程如图3所示。

在处理有环图的过程中要保持平衡准则：在处理整个有向环的前后，有向环中定义的数据传递关系不能有增加或缺失。有环有向图与AOE网惟一的区别在于有无环，本质的区别在于排序过程中是否会存在所有顶点都有前驱的情况。以这种思路考虑，问题就变得相当简单，即在拓扑排序过程中加判断，当拓扑排序遇到环时，拆掉环变成无环有向图，对于拆掉的弧线，保留其数据传递关系，然后继续拓扑排序，也就是说有环有向图是一个部分顶点带有特殊传递关系的无环有向图。这种方法不仅快速地解决了有环有向图产生的问题，同时满足了平衡准则，避免了数据流失的问题。

图3　有环有向图的处理流程

示例如下：设D1为组合成员的输入成员，D5，D6为组合成员的输出成员，如图4所示。

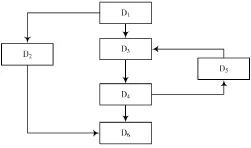
图4　存在有向环的图

首先删除初始顶点D1，判断以D1为前驱的所有顶点即D2，D3中是否存在入度不为0的顶点，D3是入度不为0的顶点，也就是说发现D3是环路的汇合点，那么组合模型内部必然存在闭环的问题。此时删除D5⁃D3的弧线，改为D5⁃结束点的弧线，如图5所示，经过开环处理后原图成为DAG图，与此同时D5⁃D3的订购关系依然存在于仿真运行过程中。

4　缺陷分析

在这种有向环处理的过程中，会产生数据滞后一个时钟周期的现象。产生数据滞后的原因是：在解开环的过程中，会根据一个点的入度来解开数据的传递关系。如图5所示，在解开D5→D3的数据传递关系过程中，当D5和D1的值同时传递到D3时，才能有数据的更新。在第一步时，D5是将从XML中读取到的初始值作为数据传入D3；第二次时，D5是将第一次处理过后得到的数据传入D3，这样在D5这个内部成员的数据处理中，得到的值总是上一个时钟周期的值，这样在D5这里有效数据就产生了一个时钟周期滞后的现象。

图5　有向环解环过程中的滞后

5　结论

本文基于HLA仿真模型理论，提出模型组合的概念，在不破坏原有数据传递关系的前提下，对多个仿真成员进行组合，从而减少实际加入联邦的成员数量，阐述了对仿真成员进行组合的理论基础。通过对不同描述文件的读取实现普通的通用模型和组合模型之间的切换，提高了模型的重用率，减少了对仿真模型进行开发的成本消耗。

［1］蒋晓原.HLA仿真程序设计［M］.北京：电子工业出版社，2002：11⁃12.

［2］雷永林.仿真模型重用理论、方法与异构集成技术研究［D］.长沙：国防科学技术大学，2006.

［3］吴义明，齐欢.基于HLA的城市交通控制系统仿真［J］.计算机仿真，2004，21（6）：159⁃161.

［4］李震，余银，刘向东，等.一种应用于HLA分布式仿真方法的通用联邦成员：中国，CN103514321A［P］.2014⁃01⁃15.

［5］姜丽丽.基于HLA的中间件方法研究及工具设计［D］.长沙：国防科学技术大学，2006.

［6］王志勇，李志猛，凌云翔，等.HLA仿真的模型体系和支持工具研究［J］.计算机仿真，2005，22（5）：115⁃119.

［7］朱国华，王杰，余维伟.一种可重用可组合的并行仿真模型技术分析［J］.电子测试，2014（22）：28⁃30.

［8］PAGE E H，BRIGGS R，TUFAROLO J A.Toward a family of maturity models for the simulation interconnection problem ［C］//ProceedingsoftheSpringSimulationInteroperability Workshop.［S.l.］：IEEE，2004：123⁃129.

Research on HLA⁃based combination technique of simulation members in model level

ZHU Guohua，DING Jianjun，YANG Chen，DAI Yang
（College of Mathematics and Computer Science，Jianghan University，Wuhan 430056，China）

HLA（high level architecture）interface is packaged usually in the form of COM serviced component in HLA⁃based simulation to realize reuse of simulation model.With further expansion of simulation scale，too many federal members may be generated，which may make the simulation cost increased.The concept of member combination in model level is put for⁃ward in this paper.On the basis of the federal simulation members’reusing technology based on COM，the correlation theory of the data order relationship described by digraph is discussed，and a general simulation number was designed to dispatch multi⁃ple simulation models according to the digraph.Under the premise of no destruction of data transmitting relation among mem⁃bers，multiple simulation members are combined into a federal simulation member to reduce the number of federal simulation members and the cost of simulation.

HLA simulation；federal member；model combination；data order

TN915⁃34

A

1004⁃373X（2016）12⁃0010⁃04

10.16652/j.issn.1004⁃373x.2016.12.003

2015⁃11⁃11 基金项目：国家科技支撑计划专题项目（2013BAD11B02⁃06）；武汉市科技局产学研项目（cxy201405）

朱国华（1969—），男，山东胶州人，讲师，博士。主要研究方向为软件工程、并行仿真。