一种新型微分平坦无极灯镇流器的研究

鲁　刚，吴高阳，赵佳伟，陈延明

（广西大学 电气工程学院，广西 南宁　530004）

一种新型微分平坦无极灯镇流器的研究

鲁刚，吴高阳，赵佳伟，陈延明

（广西大学 电气工程学院，广西 南宁530004）

为了改善无极灯的效率和性能，设计一种基于微分平坦理论控制的无极灯镇流器。通过引入微分平坦理论，使用李雅普诺夫稳定性原理设计出控制策略，既可以保证系统的稳定性与可靠性，还可以提高系统的效率。该文分析了Boost升压变换器的微分平坦性，构造了李雅普诺夫能量函数及确定其控制规律，分析了控制策略的可行性与正确性。最后，基于DSP2812制作了一台100 W的实验样机，实验结果表明，基于微分平坦控制理论设计的控制系统具有稳定性好、调节能力快以及效率高等优点。

微分平坦理论；稳定性原理；无极灯镇流器；李雅普诺夫函数

0　引言

无极灯因其光效高、寿命长、高显色、环保等优点被广范应用于城市亮化、泛光照明、隧道、照明下水灯等照明领域，尤其适用于高危或维护费用高等重要场合。节能环保的无极灯与LED灯成为继HID灯后新型第四代照明光源［1⁃4］。但是无极灯也因其成本、电磁干扰、散热和可靠性差的问题，制约其发展与应用。

微分平坦理论的提出［5］，为电力电子系统非线性控制提供了一个良好的选择。文献［6］表明如果一个系统是微分平坦系统，那么这个系统可以等效为一个线性可控系统；文献［7］的研究表明，三相电压源变换器（VSC）是微分平坦系统，且运用非线性的控制方法是最自然的、最合适的，因为它可以直接补偿系统的非线性特性而不需要一个线性的近似值去补偿；文献［8］提出李雅普诺夫稳定性理论与微分平坦控制相结合导出控制规律，使得控制系统的鲁棒性、稳定性、动态响应能力和抗干扰性能得到提高；文献［9］研究成果表明应用微分平坦理论控制的三相逆变器具有更好的鲁棒性和动态性能。

为了获得更高的效率和综合性能，无极灯镇流器主电路采用传统升压电路，结合微分平坦控制策略与李雅普诺夫理论，推导微分平坦升压电路控制规律，搭建输入功率负反馈系统。

仿真与实验结果表明基于微分平坦升压控制策略搭建的无极灯镇流器具有稳定性好、快速调节、高效等优点。

1　微分平坦控制理论

微分平坦理论的控制方法是一种非线性控制方法。微分平坦控制定义如下：如果在微分平坦系统中可以找到一组输出变量y（平坦输出），使其不通过任何积分运算就可以决定所有状态变量x和控制变量u，满足：

则此系统属于微分平坦系统。一般控制变量维数大于输出变量维数，输入变量维数大于输出变量维数。由式（1）可知微分平坦理论的一个重要性质，即状态变量x和控制变量u可以根据平坦输出y及其有限阶微分直接给出，而不需要通过求解微分方程。如图1所示为基于微分平坦理论设计的系统控制框图。

图1　微分平坦系统框图

2　控制系统的数学模型

2.1系统的建模与微分平坦性

如图2所示为微分平坦升压主电路拓扑结构，通过对输出电压、电感为电流采用开关周期平均运算，保留原信号低频部分，滤除开关频率分量和开关频率谐波分量。在稳态量的基础上引入电感电流，输出电压和占空比扰动量，根据基尔霍夫定理列出系统微分动力学系方程如下：

式中，u′=1-u，u为占空比。

图2　微分平坦升压主电路拓扑

输出电压对占空比输出传递函数是一个二阶系统，不是一个标准的微分平坦系统。本文以输出功率作为输出变量，输入电流作为输入变量，占空比作为控制量，式（2）转化为：

系统状态变量u和输入变量（输入电流I）i可以根据平坦输出（输入功率P）i及其有限次微分表示，为：

带有恒功率负载的升压电路满足微分平坦性。因此，带有恒功率负载的升压变换器是平坦系统。无论对功率型负载还是对电阻型负载，升压电路动力学方程均可用式（2）表示，经坐标变换均可表述成如式（4）所示的微分平坦系统。

2.2控制器的确定

根据系统性能指标：构造输入功率误差e2和输出误差积分e1加权平方的能量函数，输入功率稳态误差为零，输入功率稳态误差积分尽量小，保证系统稳定，抗干扰能力强等优点。

构造李雅普诺夫函数V的一般形式如下：

由式（4）～式（6），根据李雅普诺夫系统稳定条件和李雅普诺夫导函数小于零，系统大范围渐进稳定。导出系统控制规律：

2.3控制系统设计

（1）系统开环传递函数。恒功率输出的微分平坦升压电路主电路采用常规升压电路，占空比到输入功率的传递函数：

（2）系统控制规律。根据微分平坦性质得出的控制规律式（7），经拉普拉斯变换得到控制系统传递函数：

（3）系统闭环传递函数。根据图3，微分平坦升压电路闭环传递函数：

闭环控制系统控制框图如图3所示，具体实现过程：电路检测直流输入电压、电流，相乘得到直流输入功率信号与给定输入功率比较，经过微分平坦调节器得到电压误差信号，与三角波比较形成PWM信号经过隔离驱动开关管。

图3　功率闭环控制框图

3　实验验证

3.1Matlab仿真

为了验证本文提出的微分平坦控制方法的正确性和有效性，本文利用Matlab软件搭建恒功率输出的微分平坦升压系统，仿真参数如下：输入交流电压Vi=50 V，基波频率fr=50 Hz，输出功率P=100 W，开关频率fs=100 kHz，输出滤波电容 C=220 μF、电感L=0.5 mH、常数k= 20 000，k1=0.6，k2=1。图4表明系统动态过程为：系统经过短暂调整时间小于25 ms后稳定，系统响应速度快。图5表示系统稳态过程：系统反馈功率跟随给定功率变化且等于给定输入功率，恒功率输出，系统稳定，满足系统设计要求。

图4　系统输出仿真曲线

图5　反馈功率、输出电压曲线

3.2实验结果

为了验证控制策略的可行性与正确性，本文制作了一台恒功率输出的微分平坦升压变换器样机，参数如下：输入电压20～60 V；线路频率fr=50 Hz；输出功率P= 100 W；开关频率fs=100 kHz；输入电感L=0.5 mH；输出电容C=220 μF。如图6所示为微分平坦升压电路结构框图，数字控制采用TI公司数字处理器TMS320F2812控制芯片。数字功率调节器通过电压霍尔传感器、电流霍尔传感器检测输入电压、输出电压、输入电流，经过微分平坦运算，输出PWM控制信号。

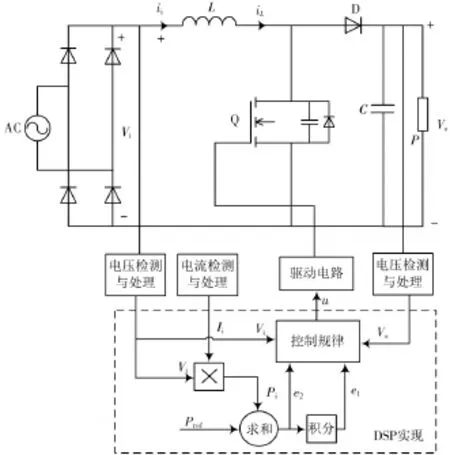
图6　微分平坦升压电路拓扑

实验结果如下：

（1）驱动波形。驱动电压与漏源极电压波形见图7。

图7　驱动电压与漏源极电压波形

（2）负载跳变波形。给定功率100 W时负载跳变波形如图8所示。

（3）输出电压波形。输出电压波形如图9所示。

图7为升压电路开关管驱动波形：开关管高电平16 V开通，低电平0 V关断。图8为负载跳变波形：给定功率100 W，负载由100 Ω到200 Ω（200 Ω到100 Ω），实测输出电压由99.6 V到140.1 V（140.1 V到99.6 V），即输出功率由99.20 W切换到98.14 W，且系统调整时间小于25 ms。图9为变换器输出电压及纹波波形：给定功率100 W时，输出电压稳定100 V，纹波电压小于1 V，即输出电压纹波小于1%。

图8　给定功率100 W时负载跳变波形

图9　输出电压波形

4　结论

本文基于微分平坦理论，采用李雅普诺夫稳定性原理设计出输出恒功率Boost变换器的控制策略，研制了一台100 W的无极灯镇流器样机。该样机输出功率恒定，电压在100～200 V范围内可调。通过仿真分析与实验结果可知，无极灯整流器采用微分平坦控制策略能够具有稳定性好、调节能力强以及效率高等优点。该微分平坦控制策略也可以推广到其他电路拓扑，如Buck，Fly⁃back，Cuk等，搭建控制系统用于通信、照明等多个应用领域。

［1］张静宇.高压钠灯电子镇流器的研究与设计［D］.长沙：中南大学，2013.

［2］程磊.数字式的金卤灯电子镇流器研究与设计［D］.南京：南京理工大学，2013.

［3］俞忆洁.高性能LED背光源驱动器的研究［D］.南京：南京航空航天大学，2014.

［4］马红波，郑聪，余文松.无电解电容的改进型SEPIC LED照明驱动［J］.电工技术学报，2012，27（6）：139⁃146.

［5］FLIESS M，LEVINE J，MARTIN P，et al.A Lie⁃Backlund ap⁃proach to equivalence and flatness of nonlinear systems［J］. IEEE transactions on automatic control，1999，44（5）：922⁃937.

［6］PAHLEVANINEZHAD M，DAS P，DROBNIK J，et al.A new control approach based on the differential flatness theory for an AC/DC converter used in electric vehicles［J］.IEEE transac⁃tions on power electronics，2012，27（4）：2085⁃2103.

［7］RIGATOS G，SIANO P，ZERVOS N，et al.Control of three ⁃phase voltage source converters with the derivative⁃free non⁃linear Kalman filtering［C］//Proceedings of 2013 39th IEEE Conference on Industrial Electronics.Vienna：IEEE，2013：7590⁃7595.

［8］PHATIPHAT T，SERGE P.A new control law based on the dif⁃ferential flatness principle for multiphase interleaved DC⁃DC converter［J］.IEEE transactions on circuit and systemsⅡ，2010，57（11）：903⁃907.

［9］RIGATOS G，SIANO P，ZERVOS N，et al.Nonlinear control of the three⁃phase inverter using the derivative⁃free nonlinear Kalman filter［C］//Proceedings of 2015 11th IET International Conference on AC and DC Power Transmission.Birmingham：IET，2015：1⁃7.

［10］RIGATOS G.Nonlinear control and filtering using differential flatness approaches［M］.Berlin：Springer，2015：25.

Research on a new electrodeless⁃lamp ballast based on differential flatness

LU Gang，WU Gaoyang，ZHAO Jiawei，CHEN Yanming
（College of Electrical Engineering，Guangxi University，Nanning 530004，China）

In order to improve the efficiency and performance of the electrodeless light，an electrodeless⁃light ballast based on the theory of differential flatness control was designed.The control strategy was designed by introducing the theory of differen⁃tial flatness and using the Lyapunov stability principle，which can ensure the system stability and reliability，and improve the system efficiency.In this paper，the differential flatness of Boost converter is analyzed，Lyapunov energy function is constructed and its control strategy is determined，and the feasibility and correctness of the control strategy are analyzed.An experimental prototype with 100 W was developed based on DSP2812.The experimental results show that the control system based on the theory of differential flatness has the advantages of good stability，fast adjustment and high efficiency.

theory of differential flatness；stability principle；electrodeless⁃light ballast；Lyapunov function

TN602⁃34

A

1004⁃373X（2016）12⁃0126⁃04

10.16652/j.issn.1004⁃373x.2016.12.034

2015⁃11⁃02 基金项目：广西自然科学基金（2014GXNSFAA118380）

鲁刚（1990—），男，陕西榆林人，硕士研究生。主要研究方向为电力电子技术与电源系统。