基于CAD光相位模型的数字全息检测方法研究

肖　文，李玉旺，潘　锋

（北京航空航天大学 仪器科学与光电工程学院 教育部精密光机电一体化技术重点实验室，北京　100000）

基于CAD光相位模型的数字全息检测方法研究

肖文，李玉旺，潘锋

（北京航空航天大学 仪器科学与光电工程学院 教育部精密光机电一体化技术重点实验室，北京100000）

针对数字全息的精密机械结构三维检测中相位的跃变，在分析相位包裹产生的机理基础上，提出一种建立被测物体计算机三维辅助设计（3D⁃CAD）的光相位模型并进行解包裹的方法。将3D⁃CAD模型点云化处理，构建相位分布测量模型，获取被测物的相位图；通过搭建的双波长数字全息实验系统，拍摄被测物体的全息相位图并与模型的相位图进行初始对准和位置精确对准，计算全息图的包裹相位所对应的真实差值，获得全息测量的解包裹相位。仿真和实验分别采用不同表面形貌的被测物体，结果表明该方法对于精密结构的检测非常有效。

精密机械结构；数字全息；相位解包裹；CAD模型；精确配准

0　　引言

随着制造技术的提高，特别是智能制造技术的应用，计算机三维辅助设计（3D⁃CAD）、高精度自动加工技术在航空、航天、汽车、机床等重型装备制造行业大规模的应用，企业产品的设计效率得到了极大的提高，3D模型的精度也越来越高［1］。同时，由于计算机辅助设计功能多样化和制造过程中的智能化不断加强，加工件的精度也达到极高的水平。这样，对于精密加工件的检测也提出了较高要求，特别是测量所得三维形貌与其标准3D设计模型的比对［2］。数字全息［3］是传统全息术、计算机技术与电子成像技术结合的产物，其利用数字图像传感器CCD或CMOS记录全息图，计算机数值模拟光学的衍射过程，定量获得光波的振幅和相位信息，具有快速实时、非接触、全场测量、分辨率高等优点，已被广泛应用于精密物体的形貌测量中。将数字全息测量与计算机辅助设计3D实体模型结合，可以定量地比对实际加工件与标准模型的匹配程度，精确再现加工件的形貌参数与加工误差。然而由于精密加工件的表面高度跃变，用数字全息测量再现得到的相位是一个包裹相位。包裹相位受到［-π，π］周期的约束，难以反映被测物体真实三维形貌，也难以与标准3D实体模型进行直接比对。

针对全息图相位包裹问题，国内外学者提出了多种解决方法，主要包括数值解包裹［4⁃6］和光学解包裹。数值解包裹主要包括基于路径解包裹算法和最小Lp范数法等，该算法适用于光滑、连续表面的解包裹，当测量表面存在高度跃变或测量噪声过大时，该算法就难以解决相位包裹问题；光学解包裹主要包括双波长相位解包裹［7⁃8］和多波长相位解包裹［9］，该方法通过构建合成波长，可以一定范围内扩大测量的纵向深度，然而对于高度跃变较大的精密加工器件，此方法仍然难以达到测量效果。

针对测量表面高度跃变产生的解包裹问题，Berg⁃ström P等人提出利用3D⁃CAD相位模型［10］进行指导解包裹的方法，对于高度跃变表面的包裹相位进行展开处理，恢复了测量物体的三维形貌。然而在测量过程中，其在物光波中引入了透镜进行干涉成像，构造产生的球面光波，使物体对应相位产生畸变［11］。另外，其对于CAD模型初始相位信息［12］的获取较为复杂。

本文提出一种利用被测物体CAD光相位模型信息，对精密机械结构高度跃变表面进行指导解包裹的改进方案。在光路设计方面，摒弃了物光波中透镜的设置，避免了物镜所带来的球面光波而引起的相位畸变，使得包裹相位更加准确地表示物体垂直高度分布。在CAD光相位模型获取方面，以精准的点云数据来代替CAD模型高度跃变表面并以此构建CAD模型相位分布，方便、快捷、高精度地得到了标准设计模型的高度分布，其对后续相位分布的计算也相当的方便。仿真和实验结果表明，该方案可以实现精密机械结构的原位检测，同时其检测精度可以达到一个合成波长量级。

1　理论分析与方法

1.1相位解包裹算法原理

测量过程中，真实相位与包裹相位之间的关系如下：

式中：φobject（x，y）为物体表面所对应的真实相位；φwrapped（x，y）为测量所得物体表面包裹相位，其对应点之间存在n×2π相位差值。

相位解包裹的任务是要从包裹相位中确定正确的n值，然后在相应点加上（或减去）n×2π，从而得到真实的相位场。

1.2基于CAD数据解包裹原理

随着计算机技术的不断发展，计算机辅助设计3D实体模型设计精度越来越高，其所构建的3D实体模型包含设计物体精确的形状和属性信息，可作为实际加工件的标准模型。因此，对实际精密加工件的相位处理，可利用一定光照条件下获取的标准3D⁃CAD相位模型对实际包裹相位做一个指导，以获取其真实相位。

在相同波长条件下，基于垂直平行光照射实际物体所得相位与模拟垂直平行光照射3D⁃CAD模型所得相位之间的关系为：

式中：φCAD（x， y）为CAD模型相应表面所对应的相位；φobject（x，y）为实际物体表面所对应的无包裹的相位；δ为相位差值；C为选取相位基准差值。

结合式（1），CAD模型对应相位与测量实际物体所得包裹相位之间的关系为：

当实际物体相位与其CAD模型相位差值即δ在［-π，π］之间时，通过CAD模型相位求得的n×2π就是包裹相位所对应真实相位差。根据此关系，对实际物体和其3D⁃CAD模型在相同的特定波长下进行测量，保证相位差值δ在［-π，π］之间，利用公式：

可求得解包裹后的相位值。C作为相位基准差值对相位差值计算无影响。

1.3建模流程

1.3.1CAD模型初始相位信息获取

CAD模型由多种标准文件格式组成，STL格式［13⁃14］即三角网格表示形式，因其简单、易操作、适用性强等特点，已被广泛应用于CAD模型与其他系统之间的数据传递中。将标准CAD模型以STL格式存储，获得CAD模型一定密度下的三角网格化表示形式。分析STL文件格式，将其导入编程文件中，获取一定密度下包含高度信息的表面点云数据，作为CAD模型的代表。

根据光程与相位的关系：

式中：z为光程；Δφ（x，y）为相位差；λ为测量波长。对于反射型物体，当照明方向和观察方向均垂直于相位零平面时，光程为测量物体高度的2倍，可得：

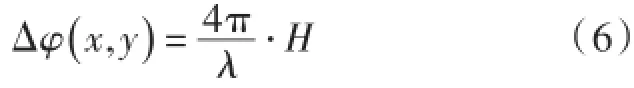
式中：H为测量物体高度；Δφ（x， y）为相位差值；λ为测量波长。由式（6）可知，相位分布只与物体表面各点到相位零平面的距离有关，若已知物体的高度信息，便可获得其相位分布差。因此，通过选取一定基准，基于垂直光照条件，获得CAD模型表面的相位分布。CAD模型相位信息需保持较高精度，其为后续的解包裹处理提供依据，同时也作为形貌检测的标准存在。

1.3.2被测物体包裹相位信息获取

搭建离轴双波长数字全息实验光路，获得被测物体的包裹相位图。双波长全息测量的实质是通过两个波长的相位图合成新相位图，新相位图相当于由一个更大的等效波长所得到。采用波长为λ1和λ2的激光，按相同的传输路径进行记录，φ1和φ2分别为其各自数值再现后的相位，h为光经过物体后产生的光程差。则两者的相位差Δφ为：

式中：

式（5）中相位差即相当于用等效波长 Λ获取的相位，显然 Λ要比 λ1和λ2大。选择合适的测量波长，既要保证相位差值δ全部位于［-π，π］之间，又不要合成波长过大，使得信噪比太低和测量精度下降。

1.3.3CAD模型相位与测量所得包裹相位的匹配解包裹

利用CAD模型相位对测量所得包裹相位进行指导解包裹，不可避免地要解决两相位图点对点的精确匹配问题。相位匹配分为两部分进行：初始匹配和精确匹配。

初始匹配中，在待配准和基准两幅图像中［15］选择控制点来确认图像中的相同特征和标志，根据控制点的位置来推算某种空间映射的关系，利用该空间映射的关系对待配准图像进行几何变换，达到两图像的初始匹配。然后以初始匹配为基础，进行相位的精确配准。

精确配准中，首先利用CAD模型相位对包裹相位进行初次解包裹运算。将解包裹后的相位与CAD模型相位利用ICP算法［16⁃17］进行精确匹配，并对CAD模型相位进行几何变换，变换后的相位在位置上更加接近包裹相位。利用变换后的CAD模型相位，再对包裹相位进行解包裹，同时判断其解包裹后的相位是否存在与原形貌特征明显不符部分。若不存在，则停止；若存在，则说明部分相位点没有得到正确解包裹，继续迭代，直到解包裹相位满足被测物体基本形貌，然后停止，输出解包裹后的相位。

2　仿真与实验

2.1仿真分析

构建表面含有高度差的3D⁃CAD模型，如图1所示。CAD模型为直径为26.00 mm的半圆柱；长度为20.00 mm；平面与最高点高度差为2.26 mm。通过点云化处理CAD模型，选取适当合成波长（0.70 mm，小于表面最大高度差），利用式（6）获得CAD模型光相位分布，截取一部分如图2所示。

图1　CAD模型

图2　模型相位图（三维）

将相位以0相位平面为基准，进行相位包裹，包裹相位如图3所示。保持包裹相位图不变，将CAD模型相位图进行旋转和平移操作。以此模拟在两相位图对准存在偏差情况下解包裹情况。

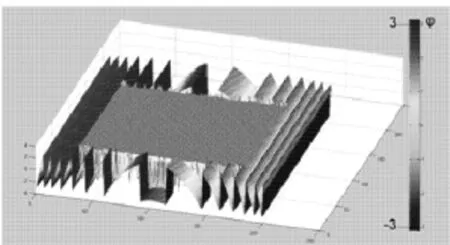
图3　包裹相位图（三维）

经过位置精确匹配和利用式（4）对包裹相位解包裹后的相位分布如图4所示。

图4　位置匹配解包裹相位（三维）

从图4中可以看出，包裹的相位得到了展开，恢复了CAD模型初始相位分布。对于结果中相位值大于初始最大值的点，为计算过程中平面与相交曲面结合处的插值误差所致。

2.2实验研究

2.2.1实验装置与实验对象

实验采用反射式离轴数字全息系单统，两个用于记录的激光器分别是532.237 nm的短相干激光器（光路中加有光程补偿器）和532.037 nm的单纵模固体激光器。根据式（8）计算可得两波长的等效波长为1 416 μm。所用CCD分辨率为1 024 pixel×1 024 pixel，像素尺寸为6.7 μm×6.7 μm。实验中没有在物光波中使用透镜进行汇聚成像，避免了由于成像模型自身光程差所引起的相位畸变问题。对于因为离轴和光线曲率等问题产生的相位畸变，已在后续的全息图处理中得到补偿。实验装置如图5所示。

图5　双波长全息实验光路示意图

同时，在获取全息图过程中，采用了多角度照射与相位叠加平均的方法［18］，大大提高了相位信息的信噪比和清晰度。实验对象为三个高度垂直分布的平面，直径从外向内分别为20.0 mm，15.0 mm和10.0 mm，三平面高度分别为5.0 mm，7.0 mm和10.0 mm，加工误差为0.5 mm以内。测量物体与其CAD模型如图6所示。

图6　被测物体与其CAD模型

2.2.2结果与分析

CAD光相位模型的三维显示如图7所示，截取一部分实验所得包裹相位图的三维显示如图8所示。

图7中CAD模型相位完整的代表了被测物体的形貌特征，将以此为标准来指导包裹相位的展开。而从图8可以看出，测量所得包裹相位图分为三个较为明显的平面，所有相位值都位于［-π，π］之间。

图7　CAD模型相位（三维）

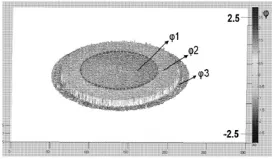
图8　包裹相位（三维）

经过两相位图精确匹配后解包裹得到的物体高度分布如图9所示，取同一直线位置解包裹后高度与标准CAD模型高度分布如图10所示。

图9　解包裹后高度分布（三维）

图10　解包裹后高度与CAD模型高度（一维）

从图9中可以看出，包裹相位已完全展开，恢复了物体真实形貌结构。而在图10中，物体高度与标准CAD模型尺寸存在一定差值（但全部位于半个波长以内），可能原因为加工过程中物体尺寸出现了偏差和测量波长的精度存在较小偏差。而对于平面中存在的密密麻麻的突起，则可能是由于测量过程中的噪声引起或是物体本身存在的误差。另外，连接两平面之间的斜线则是点云获取过程中的插值所致，通过增加点云密度可以一定程度减小该插值影响。

3　结论

本文提出一种基于CAD光相位模型进行全息相位解包裹，然后将三维测量结果与CAD标准模型进行比对的方法。针对此方法，首先进行仿真分析，仿真对象为光滑曲面中存在的高度跃变，将高度跃变表面保存为包裹相位形态，然后利用标准设计模型相位对包裹相位进行包裹展开处理，结果较好地恢复了原始相位信息。然后开展实验验证，实验对象为具有垂直高度跃变的圆柱形物体。将利用双波长数字全息测量光路获取的被测表面包裹相位图与标准设计实体CAD光相位模型进行匹配解包裹，结果定量恢复了测量表面的相位分布，并将该测量结果与CAD标准模型进行了比对，结果表明该方法可以解决精密机械结构在数字全息测量中的三维显示问题。测量结果与CAD模型的高度偏差代表了实际精密机械结构的加工误差，其受到测量波长精度和两相位模型匹配精度的影响。后续研究可从提高测量波长精度和提高相位图匹配精度方面进行研究。本文在实际测量过程中对于透镜的去除和利用点云数据对CAD标准模型的构建使得该方法更加的简便、快捷，一定程度提高了测量精度，为包裹相位的展开提供了新的思路。

［1］李亨昭，邱敬之.先进制造技术的发展趋势与战略设想［J］.电子机械工程，2000（2）：3⁃6.

［2］ZHANG Xuechang，XI Juntong，YAN Junqi.Research on digi⁃tal measurement technology based on point cloud data of com⁃plex surfaces［J］.Computer integrated manufacturing systems，2005，11（5）：727⁃731.

［3］KÜHN J.Multiple⁃wavelength digital holographic microscopy ［D］.LAUSANNE：École Polytechnique Fédérale De Lausanne，2009.

［4］JUDGE T R，BRYANSTON⁃CROSS P J.A review of phase un⁃wrapping techniques in fringe analysis［J］.Optics and lasers in engineering，1994，21（4）：199⁃239.

［5］崔鹏.数字全息面形测量中的相位解包裹技术研究［D］.天津：天津大学，2007.

［6］王新，贾书海，陈光德.相位去包裹技术进展［J］.仪器仪表学报，2005，26（z2）：665⁃668.

［7］郑箫逸.双波长数字全息干涉及其在光学测量中的应用研究［D］.济南：山东大学，2012.

［8］王羽佳，江竹青，高志瑞，等.双波长数字全息相位解包裹方法研究［J］.光学学报，2012，32（10）：78⁃83.

［9］WAGNER C，OSTEN W，SEEBACHER S.Direct shape mea⁃surement by digital wavefront reconstruction and multiwave⁃length contouring［J］.Optical engineering，2000，39（1）：79⁃85.

［10］DIASPRO A，BIANCHINI P，CELLA ZANACCHI F，et al. Shape verification using dual⁃wavelength holographic inter⁃ferometry［J］.Optical engineering，2011，50（10）：475⁃480.

［11］张中恒.数字全息中再现像的相位畸变补偿［D］.昆明：昆明理工大学，2014.

［12］BERGSTROM P.Perspective depth extraction of points on a surface under an instantaneous rigid body transformation［J］. Asian journal of plant sciences，2012，12（2）：363⁃367.

［13］樊龙欣，曲学军，韩宁，等.点云与CAD模型配准预处理技术的研究［J］.数字技术与应用，2013（11）：66.

［14］肖苏华.三维CAD实体文件转化STL文件格式精度研究［J］.模具工业，2014（9）：12⁃14.

［15］常学义，孙秋冬，任煜，等.基于MATLAB的图像配准方法［J］.上海第二工业大学学报，2006，23（4）：303⁃308.

［16］ZHANG Z.Iterative point matching for registration of free⁃form curves［J］.International journal of computer vision，1992，13（2）：119⁃152.

［17］戴静兰，陈志杨，叶修梓.ICP算法在点云配准中的应用［J］.中国图象图形学报，2007，12（3）：517⁃521.

［18］YAN L，WEN X，FENG P，et al.Coherent noise suppression of phase images in digital holography by rotating illuminating light［J］.High power laser and particle beams，2013，25（6）：1345⁃1350.

Research on digital holographic detection method based on CAD optical phase model

XIAO Wen，LI Yuwang，PAN Feng
（Key Laboratory of Precision Opto⁃mechatronics Technology of Ministry of Education，School of Instrumentation Science and Opto⁃electronics Engineering，Behang University，Beijing 100000，China）

Aiming at the phase jumps in 3D detection of digital holographic precision mechanical structure，and on the ba⁃sis of the analysis of the generating mechanism of phase wrapping，a new method is proposed to establish the 3D computer aided design（3D⁃CAD）optical phase model of the measured object and conduct for phase unwrapping.The 3D⁃CAD model is pro⁃cessed with point cloud to construct the phase distribution measurement model，and obtain the phase map of the measured ob⁃ject.The holographic phase picture of the measured object is taken by means of the established dual⁃wavelength digital holo⁃graphic experiment system，and conducted for initial alignment and position perfect alignment with the model’s phase diagram. The difference value between the wrapped phase and its corresponding true phase of the holography diagram is calculated to ac⁃quire the unwrapped phase of holographic measurement.The measured objects with different surface topography were respective⁃ly used in simulation and experiment.The results indicate that the proposed method is effective to detect the precision structure.

precision mechanical structure；digital holography；phase unwrapping；CAD model；accurate registration

TN26⁃34

A

1004⁃373X（2016）12⁃0001⁃05

10.16652/j.issn.1004⁃373x.2016.12.001

2015⁃10⁃10 基金项目：国家自然科学基金资助（61177006）

肖文（1962—），男，陕西人，教授，博士。主要从事数字全息检测及干涉测量方面的研究工作。李玉旺（1992—），男，山东人，硕士。主要从事数字全息精密机械结构三维检测方面的研究工作。潘锋（1979—），男，广西人，副教授，博士。主要从事数字全息检测及干涉测量方面的研究工作。